微阴极电弧推力器磁路设计
2018-11-19,,,,
,,,,
1. 北京控制工程研究所,北京 100190 2. 北京市高效能及绿色宇航推进工程技术研究中心,北京 100190 3. 大连理工大学 工业装备结构分析国家重点实验室,大连 116024
微阴极电弧推力器(Micro-Cathode Arc Thruster,简称μCAT)[1]是由美国乔治华盛顿大学近年来研制的一种新型推力器,其利用真空条件下放电电弧烧蚀阴极材料产生较高电离度的高速等离子体,并利用外加磁场聚焦等离子体以产生推力[2]。
典型的环型μCAT推力器如图 1所示,主要包括阳极、阴极、电极间的陶瓷绝缘层和同轴的外磁线圈等[3-4]。为了便于研究,可以人为地将整个工作过程分为两个阶段:首先,脉冲放电的真空电弧在阴极表面收缩成电流密度很高、且在磁场作用下不断运动的阴极斑点,烧蚀阴极材料形成较高电离度的高速等离子体;随后,高度电离的等离子体在多物理场耦合作用下加速喷出,产生推力[5-8]。前期研究表明,外加磁场对推力器的工作特性及可靠性具有很大影响,是整体推力器设计中的关键环节[9-13]。
1 磁路系统设计
1.1 磁路系统设计目的
磁路系统主要作用在于提高推力器工作稳定性、延长工作寿命、提高推力器比冲等推力器性能指标。经过对真空电弧的研究,阴极表面电弧激发处即阴极斑点做无规则随机运动,当有外加磁场存在时,磁感应强度能分解为横向和纵向分量,阴极斑点在磁感应强度横向分量的作用下做均匀的圆周运动,配合弹簧提供轴向力,使阴极能够均匀进给,从而使推力器阴极烧蚀更加稳定,延长推力器工作寿命。相关研究[2,4,14]表明外加磁场的存在对推力器离子起到轴向加速的作用,推力器产生的电子被外加磁场捕获约束在磁力线附近,低速的离子由于双极扩散电场的作用,聚集于电子聚集区附近并加速喷出,将方向各异的离子速度转化为轴线上的离子速度,从而可提高推力器的比冲,此外对推力器羽流等离子体具有横向束流的作用,减小羽流的发散角。
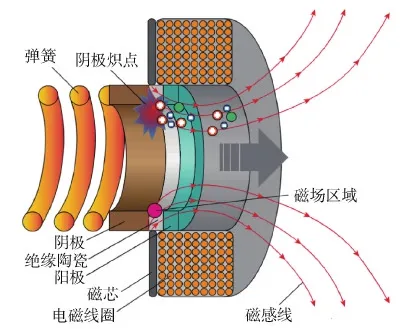
图1 微阴极电弧推力器示意Fig.1 Schematic diagram of micro-cathode arc thruster
1.2 磁路系统设计
推力器磁路系统主要由通电多匝线圈和磁芯部分组成,其中磁芯的作用是增强多匝线圈的磁感应强度,因此在进行推力器磁路系统的初步设计时可以参考多匝通电螺线管磁场计算公式,结合推力器的设计尺寸对推力器磁路系统尺寸进行初步的设计,再利用二维磁场仿真软件及三维有限元分析软件进行磁场的模拟仿真,来确定最终磁路系统设计方案。为了研究方便,本文中磁路设计为磁场位置可调、磁场大小可通过安匝数调整的可调节磁路,放电通道轴线处最大磁场可达到0.3 T。
1.2.1 线管静磁场求解的一般方法与模型
通电螺旋管的静磁场计算较为复杂,主要由毕奥-萨伐尔定律描述[15]。一般情况下多层螺线管产生的静磁场计算方法如下:共有N匝线圈,螺线管内径α1,外径为α2,螺线管长为L,通有电流I,在z方向有mz根导线,在r方向有mr层导线。图2为螺线管离散示意。
将每个导线处理为离散的源点,每个源点为单个环形线圈的作用,最终空间的磁场分布为各个离散源所产生的磁感应强度的叠加,对空间点P(rp,zp)的磁感应强度计算式为:
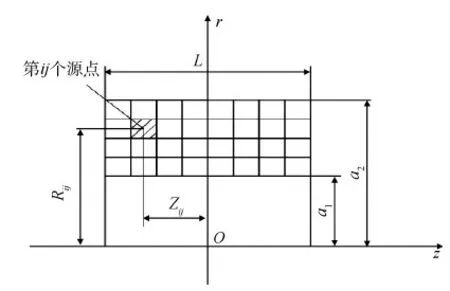
图2 螺线管离散示意Fig.2 Discretization of solenoid
式中:rij和zij为第i、j个离散源中心坐标;rp和zp为计算的空间点的坐标;K、E分别为第一类完全椭圆积分和第二类完全椭圆积分,可展开为级数式如下:
其中k有:
计算式K、E级数后面的项随次数增高急剧衰减,可用前面的有限项数计算结果代替E、K的值。因而可用上面的计算式,逐个计算网格点上的r、z方向的磁感应强度。
1.2.2 螺线管静磁场求解的简化模型
参考国内外研究进展,有一种更简便的螺线管静磁场求解方法,具体模型如下:
式中:r、z为相对于螺旋管中轴线中点为原点的坐标系下的坐标;B0=μ0nI;φ为极角,范围为[0,2π]。
M1=R2+L2/4+r2-Lz+z2-2Rrcosφ
M2=R2+L2/4+r2+Lz+z2-2Rrcosφ
上式可使用复合辛普森数值积分公式:
式中:f(x)为被积函数,a,b分别为积分区间端点值;xi对应积分区间的等分点,将区间划分为M个区间xi~(x0,x1,…,xM);h为区间长度,有:
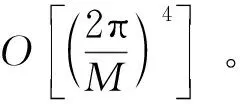
1.2.3 轴向磁感应强度的计算模型
放电通道中心线处磁感应强度需要不大于0.3 T,这一要求主要针对磁路系统的轴线磁场分布,根据已有研究,多匝多层螺线管轴线磁感应强度的计算如下:
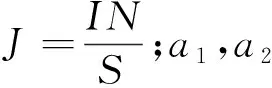
取线圈原点(Z=0)处磁感应强度B=0.3 T,结合推力器外径尺寸取线圈内外半径a1=10 mm,a2=25 mm,线圈1/2长度b=10 mm,线径为0.5 mm,真空磁导率u0=4π×10-7N·A-2,根据公式求出线圈电流密度J,当取线圈匝数N=600匝时,电流大小I=15.9 A。
2 磁路系统仿真模拟
2.1 磁路系统仿真目的
根据磁路系统初步的尺寸设计,使用二维/三维有限元分析软件进行模拟仿真,验证初步设计的结果。在模型中添加磁芯模型,改变磁芯尺寸、材料,获得不同磁场分布,根据推力器工作要求确定磁芯设计方案。验证同时通过改变电流大小、电磁线圈匝数得到不同磁路系统的磁场分布,根据推力器磁路系统的工作原理验证其是否满足推力器工作要求指标。
2.2 磁路系统二维仿真
磁路系统的设计采用二维有限元分析软件FEMM进行仿真计算。根据磁路系统设计结果确定模型尺寸,改变磁路系统的电流大小和线圈匝数仿真得到不同的磁场分布,同时可以得到磁路系统在轴线上的磁感应强度分布曲线,再通过对分布曲线进行整理,可以得到线圈电流大小和线圈匝数对电磁线圈产生磁感应强度的影响。
图3为根据磁路系统设计尺寸及初步计算结果建模,确定线圈匝数为600匝时,改变电流大小得到的线圈电流同线圈轴线磁感应强度最大值关系曲线。图4为确定线圈电流为15 A时,改变线圈匝数得到线圈匝数同线圈轴线磁感应强度最大值的关系曲线。通过曲线图可以看出线圈电流大小和线圈匝数同轴线上磁感应强度最大值成正比的关系,电流越大,磁感应强度越大;线圈匝数越多,磁感应强度越大。
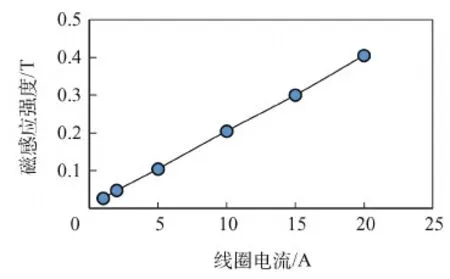
图3 线圈电流同线圈轴线磁感应强度最大值关系Fig.3 Relationship between coil current and maximum magnetic induction intensity of coil axis
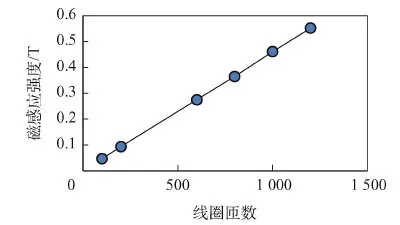
图4 线圈匝数同线圈轴线磁感应强度最大值关系Fig.4 Relationship between number of coil turns and maximum magnetic induction intensity of coil axis
通过FEMM软件计算,放电通道中心线上磁感应强度≤0.3 T,当线圈电流为15 A、线圈匝数为600匝时,轴线磁感应强度满足要求,其磁感应强度分布如图5所示,轴线上磁感应强度分布如图6所示。
经过上述二维模拟仿真,在确定并验证磁路系统电流大小及匝数的基础上,通过改变磁芯的尺寸及材料,可以得到不同磁芯对磁路系统磁场分布的影响,根据仿真结果选择合适的磁路系统磁芯。
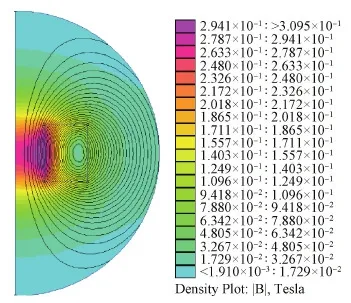
图5 磁感应强度分布Fig.5 Magnetic induction intensity distribution
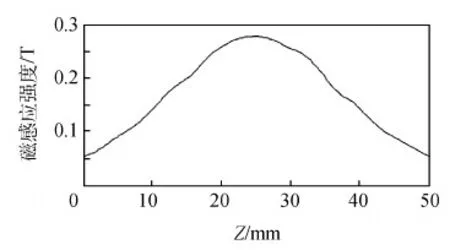
图6 轴线磁感应强度曲线Fig.6 Axis magnetic induction intensity curve
针对不同厚度的磁芯对磁场分布的影响,选用磁芯材料为纯铁,厚度分别为1 mm、2 mm、5 mm、10 mm,其分布规律相似,其中厚度为2 mm的仿真结果如图7所示,不同磁芯厚度情况下轴线磁感应强度曲线分布如图8所示。
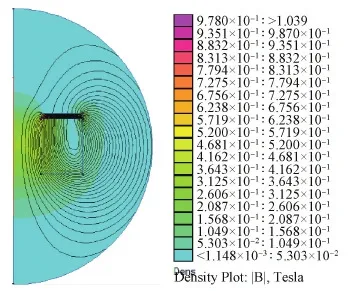
图7 厚度2 mm磁芯磁感应强度分布及轴线磁场分布Fig.7 Magnetic induction intensity distribution and distribution on the axis of a magnetic core with the thickness of 2 mm
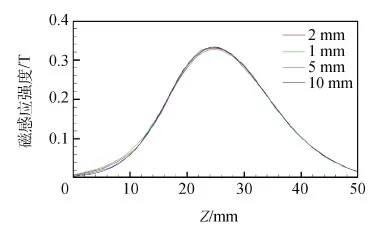
图8 不同磁芯厚度轴线磁感应强度曲线Fig.8 Axis magnetic induction intensity curve with different magnetic core thickness
对存在磁芯的磁场分布情况进行对比。当磁路系统中没有磁芯存在时,磁场分布比较均匀,同时轴线磁感应强度以轴线上Z=0为分界线呈轴对称分布;当磁路系统中加入磁芯后,磁场分布明显变化,磁场分布出现不均匀,磁芯受到线圈产生的磁场磁化后在磁芯内部及附近尤其是靠近线圈的一端形成很强的磁感应强度;轴线上磁感应强度不再以Z=0呈轴对称分布,同时轴线上的最大值较之前增加;未加磁芯的磁路系统磁感线与线圈靠近轴线的表面呈一个锐角从线圈出去,而加入磁芯的磁路系统,在加入磁芯一端,磁感线近似垂直于线圈内径表面。
不同磁芯厚度对磁场分布的影响不同。针对磁芯选择了1 mm、2 mm、5 mm、10 mm厚度,材料为软铁的磁芯模型进行仿真模拟。根据仿真结果可以分析出磁芯对磁路系统磁场分布的影响:磁芯厚度越小,磁芯内部磁感应强度越大;磁芯厚度越大,轴线上的磁感应强度最大值越大,轴线上以Z=0为分界点有磁芯的一端磁感应强度变化越快。
此外,还针对磁芯不同材料对磁路系统磁场分布的影响,选择了FEMM软件中4种导磁材料进行仿真对比,分别是软铁、低碳钢、430铁素体不锈钢、硅钢。通过仿真结果比较各种导磁材料对于磁路系统磁场分布的影响,发现这几种导磁材料对于磁场分布的影响近似相同,对于磁路系统材料的选择影响不大。
2.3 磁路系统三维仿真
磁路系统的三维仿真使用多物理场耦合有限元分析软件COMSOL进行建模计算,同二维仿真结果进行对比,验证磁路系统设计方案的可行性。利用COMSOL建立磁路系统设计的尺寸模型,分别改变线圈电流和线圈匝数仿真不同电流大小和线圈匝数的磁场分布,可以得出与用FEMM软件仿真相同的结果,即线圈电流大小和线圈匝数同轴线上磁感应强度最大值呈正比关系,电流越大、线圈匝数越多得到的磁感应强度也越大。
针对磁芯对磁路系统磁场分布的影响,主要通过对比磁路系统中有无磁芯、不同厚度的磁芯对磁路系统磁场分布的影响。无磁芯磁路系统和典型工况(磁芯厚度为2 mm磁路系统)的磁场分布仿真结果如图9和图10所示。
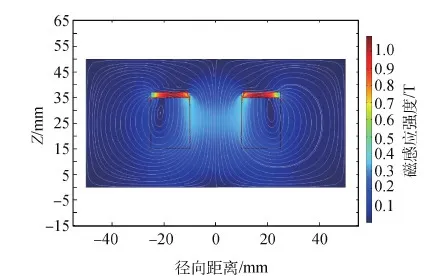
图10 厚度2 mm磁芯磁路系统磁场分布Fig.10 Magnetic induction intensity distribution of a magnetic circuit system with magnetic core thickness of 2 mm
对仿真结果进行对比分析,当磁路系统未加入磁芯时,磁场均匀分布;加入磁芯后,磁场在磁芯附近明显向磁芯偏移,磁芯内部及上表面附近的磁感线近似垂直轴线分布,磁芯靠近轴线端面附近的磁场也是近似垂直轴线,同时磁芯厚度越小,磁感线方向由轴向变为径向的速度越快。不同厚度磁芯对轴线上磁场分布的影响仿真结果如图11所示。
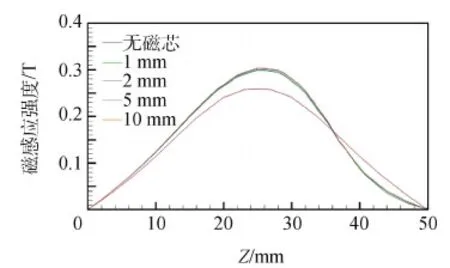
图11 磁路系统不同磁芯厚度轴线上磁场分布Fig.11 Magnetic induction intensity distribution on the axis of a magnetic circuit system with different magnetic core thickness
根据仿真结果可以分析得出,在磁路系统无磁芯时,轴线上的磁感应强度以Z=0为对称轴呈轴对称分布;系统加入磁芯后,轴线磁场分布不再呈对称分布,轴向上靠近磁芯的一端磁感应强度变化斜率更大;加入磁芯以后,轴线上磁感应强度最大值变大,同时,随着磁芯厚度变大,最大值也在变大,但是增大的差值不大。
2.4 磁路系统仿真结果总结分析
通过分别改变线圈电流大小及线圈匝数获得不同的磁路系统磁场分布,根据仿真结果可知磁路系统轴线上磁感应强度最大值与线圈电流大小及线圈匝数近似成正比,电流越大线圈匝数越多,轴线上磁感应强度越大。若需放电通道中心线磁感应强度≤0.3 T,当线圈电流≤15 A,线圈匝数为600匝时可满足设计要求。
当磁路系统中加入磁芯时,磁场分布受磁芯影响,磁感线在磁芯内部及磁芯上表面附近近似垂直轴线;轴线上的磁场分布不再以中线呈对称分布,有磁芯的一端磁感应强度的变化速度快于没有加磁芯的一端;磁感应强度随着磁芯厚度变大而变大,但变化并非很大。根据前面对磁路系统磁场作用的描述可知,其中一个作用是在阴极与绝缘材料的交界处提供一个径向的磁场使阴极斑点能做均匀的圆周运动,因此磁芯的主要作用就是改变线圈的磁场分布,提供一个径向磁场。根据仿真结果可以看出这个磁场区域大概就是磁芯的厚度,阴极和阳极间的间隙是1 mm,所以选择2 mm厚的磁芯可满足磁路系统的工作要求。
线圈匝数600匝,通电调节电流大小0~15 A,可以获得0~0.3 T的轴线磁感应强度。
3 磁路系统磁场测量
采用HSB-A型数字特斯拉计对磁路系统的磁场分布进行测量。
磁路系统轴线磁场分布测量,以磁路系统轴线作为Z轴,改变线圈通电电流大小,分别测量线圈通电电流大小为0.5 A、1 A、3 A、5 A、10 A、15 A时轴线上的磁感应强度分布,测量位置分别为Z=0 mm、5 mm、10 mm、15 mm、20 mm、25 mm、30 mm、35 mm、40 mm、45 mm、50 mm。轴线上磁场分布测量结果如图12所示。将测量结果与仿真模拟结果进行对比,模拟结果用实线表示,测量结果用虚线表示,可以看出仿真测量结果与实际结果基本吻合。
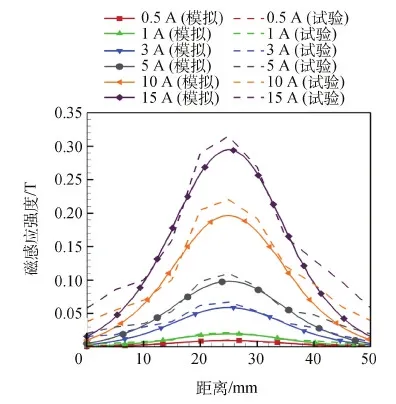
图12 轴线磁场分布测量结果Fig.12 Measurement results of axis magnetic induction intensity distribution
磁感应强度的周向不对称会导致推力偏心,因此需要对推力器通道的环形磁场进行周向均匀性的测量。选取外磁极端面为测试面,以距离壁面2 mm、半径10 mm的圆为测量路径,以一水平方向为起始测量点,以逆时针方向为角度增加方向,每45°进行一次采样测量,对周向8个点的磁感应强度进行对比分析。同时改变线圈通电电流大小,分别测量0.5 A、1 A、3 A、5 A、10 A、15 A时的磁感应强度,测量结果如图13所示。根据实际测量结果可以看出磁路系统在周向的磁场分布呈均匀分布。
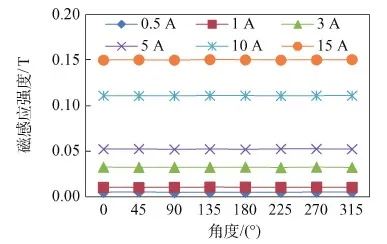
图13 周向磁场测量结果Fig.13 Measurement results of circumferential magnetic field
4 磁路系统对推力器性能影响测试
推力器性能测试主要是对推力器产生等离子体的速度进行测试,再通过改变磁路系统的磁场,分析磁路系统对推力器性能的影响。
4.1 推力器在真空下放电
推力器在真空下的放电情况如图14所示,真空舱内气压为8.2×10-4Pa,典型放电的电流电压参数如图15所示。

图14 推力器真空下放电Fig.14 Discharge of the thruster in vacuum
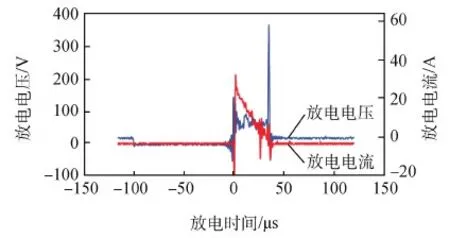
图15 放电参数曲线Fig.15 Discharge characteristic curve
4.2 推力器等离子体速度测试
测量等离子速度可以采用飞行时间法(TOF),即利用确定测量发射信号与接收信号的飞行时间间隔来实现距离测量。被测距离可表示为:
s=v×t/2
式中:s为待测距离;v为信号飞行速度;t为飞行时间。
已知信号检测装置同信号发射装置的距离,测出信号从发射装置到信号接收装置的飞行时间,再利用公式就能方便地测出信号的飞行速度。
采用双法拉第筒测量离子速度,将法拉第筒放置距推力器不同距离的位置,检测离子触发信号,利用双法拉第筒接收信号,再用双法拉第筒间的距离除以相差的接收信号时间,获得相应离子速度。将法拉第筒分别置于距离推力器一定位置,使用示波器收集信号。
改变磁感应强度的大小获得各磁感应强度下等离子体的离子速度,测量结果如图16所示。
综上所述,根据测量结果可以看出等离子体离子速度随着磁场增加而逐渐增加。
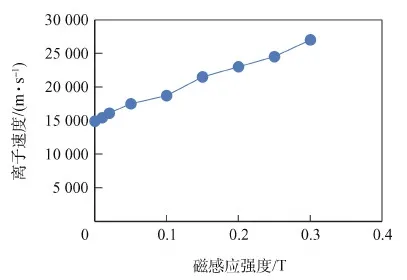
图16 不同磁场下离子速度测量结果Fig.16 Measurement results of ion velocity under different magnetic fields
5 结束语
磁场设计是微阴极电弧推力器设计的关键部分之一。本文参考多匝通电螺线管计算公式完成磁路系统初步设计,进一步采用二维和三维数值仿真研究可知:线圈电流和线圈匝数(即安匝数)直接决定磁场大小;磁芯可引导磁场的分布;4种不同导磁材料(软铁、低碳钢、不锈钢、硅钢)对磁场分布影响不大。采用特斯拉计测量磁感应强度对仿真结果进行验证。最后在真空条件下采用时间飞行法(TOF)测量不同磁场下的等离子速度可知,等离子体离子速度随着磁场增加而逐渐增加。
