基于会切场推力器无拖曳系统建模及参数优化

，，，

哈尔滨工业大学 先进动力研究所 哈尔滨 150001

地球重力场研究历来是大地测量学领域的核心任务之一。随着对空间科学任务的迅猛发展及探索任务的深入，对航天器试验环境要求也在不断提高，航天器受到的残余扰动必须尽可能减小。卫星在太空中运行时会受到各种的干扰力和力矩，其中对于低轨卫星来说，运行中的大气阻力(drag force)是最主要的干扰力。为即时补偿卫星受到的大气阻力，国外学者通过加入控制系统产生相应大小的推力来进行抵消。这种卫星称为无拖曳卫星[1](drag-free satellite)，同样的该控制系统称为无拖曳控制系统。目前发射成功的用于重力场探测的无拖曳卫星有ESA的GOCE，其于2009年3月17日发射成功，预估可达到全球大地水准面精度达到1 cm、重力异常的精度达到1～2 m/s2的目标[2]。

无拖曳控制技术起源于20世纪60年代，最初只是应用在基础物理研究上，到1959年George Pugh[3]创新性地提出可以将无拖曳控制方案和卫星轨道控制联系起来。1964年，B Lange推导出9自由度的无拖曳卫星运动方程[4]，并研究了无拖曳卫星的动力学和控制技术，从此无拖曳卫星的研究进入了一个新的时期。现在的无拖曳卫星已经发展到了第二代，为了提高系统的整体性能，内部的检测质量数目也不再限于一个[5]。

在控制策略上，PID和LQR方法经常被用来估算无拖曳控制的基本性能及设计初步的算法[6]。

由于无拖曳控制阻力补偿要求控制系统具有快速响应，宽范围、高分辨率推力调节和低推力噪声的特点，因此传统的化学发动机无法满足要求。针对此任务需求，会切场推力器(HEMPT)是目前国际涌现出的一类以霍尔推力器为基础发展起来的新型电推进系统，其工作原理如图1所示，靠电磁场的约束来加速离子从而获得推力[7]。我们设计的会切场推力器目前已进行大量数值仿真及性能试验验证，证明其具有3个数量级连续变化，有望应用在以后的重力场探测任务中。

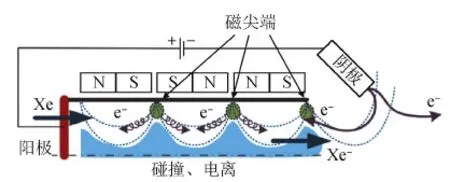
图1 会切场推力器结构原理Fig.1 Illustrative diagram of HEMPT

本文构建出卫星运行时的无拖曳控制的物理问题，并且应用相应的控制方法进行了建模，并对理想状况与考虑实际条件下的运行结果进行了分析。在建模过程中使用遗传算法对PID参数进行筛选以增强整体的控制精度。

1 无拖曳卫星动力学模型

1.1 建立空间坐标系

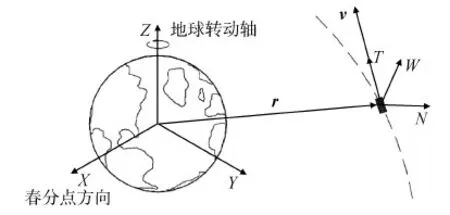
图2 GCI和NTW坐标框架Fig.2 GCI and NTW coordinate frame

对采用无拖曳控制的卫星进行建模，首先应该考虑的是其所在的坐标系。本文无拖曳卫星建模所用到的坐标系有2个，分别为是惯性地心中心(GCI)和卫星为中心的旋转框架(NTW)，如图2所示。其中GCI参考系用于定义运动方程，输入到控制律中的状态误差和计算的推力加速度。NTW框架的原点位于质心，T方向为质心前进方向；W方向为轨道角动量方向；N方向与T、W满足右手定理，该坐标系用来求取该坐标系下推力器的推力值。

1.2 无拖曳控制轨道模型

卫星内部的检测质量在运行过程中受到万有引力和地球非球形摄动的影响, 非球形摄动是由于地球并不是一个标准的球形，而且内部的密度分布也不均匀。检测质量运行过程中的加速度表达式为：

(1)

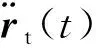
检测质量外部的近地卫星在太空运行中会受到万有引力、地球非球形摄动、大气阻力以及来自自身推力器的推力。卫星运行过程中的加速度表达式为：

(2)

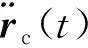
二者的加速度差值为：

(3)

1.3 无拖曳控制阻力模型

低轨卫星在运行过程中主要受到大气阻力的影响，大气阻力的表达式为：

(4)

式中：Cd为大气阻力系数；A为卫星迎流面面积；ρ(t)为卫星所在高度的大气密度；vc(t)为卫星相对于大气的速度；m(t)为卫星的总质量。

此处定义阻力系数c(t)：

(5)

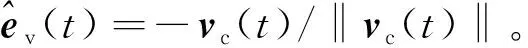
(6)

1.4 无拖曳大气阻力模型

在使用MATLAB编写程序求阻力加速度对于大气密度可以基于卫星实时的高度和位移运用4阶插值法进行求值。即使用MSISE-90模型。

1.5 无拖曳控制建模中的不确定性变量

在研究中，可以假设卫星的位置rc(t)和速度vc(t)，每10 s从全球定位系统(GPS)中获得。假设位置信息可以精确到±50 m，卫星的运行速度可以精确到±10 cm/s。所以卫星的实时位置rm(t)和速度vm(t)与GPS得到的数据有一定的误差。可以添加一个随机误差到实际状态中来模拟这些量：

(7)

不确定性向量εpos和εvel由假定的最大不确定性值乘以区间[-1 1]上的随机数向量。这两个量在GPS位移和速度向量更新的时候同时更新。

这里用Δrm(t)来表示卫星质心和卫星内部检测质量质心的位移误差矢量。假设可以精确到±5 nm。可以通过计算卫星位移矢量和检测质量的位移矢量的差来建立这个模型，并且以类似卫星位移和速度的方式将不确定性添加到其中，即得到：

Δrm(t)=Δr(t)+εΔr(t)=

[rc(t)-rt(t)]+εΔr(t)

(8)

假设GPS交付Δrm(t)的速率大约为1.9 Hz，这与计算机的采样频率一致。所以rm(t)、vm(t)和Δrm(t)可以同时被发送到控制器。在模拟最开始的时候，假定卫星的位移误差设置为最大不确定度5 nm。初始速度误差假定为零，这是因为确保检测检测质量在实际任务开始时开始数据收集。

1.6 无拖曳控制器设计

由上面的推导过程，得到现在的组合公式:

(9)

采用局部线性反馈来消去式(9)中的非线性项，出于简便性考虑，采用PID控制来实现，使用已知的卫星和参考质量的状态矢量估算推力，使推力器加速度的估算复杂程度变得最小。其中PID控制参数可通过遗传算法进行筛选，这将在下一节讲述其原理。则该控制律可以写为：

(10)

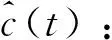
(11)

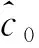
因此，状态误差方程可以改写为一个矢量二阶系统：

(12)

(13)

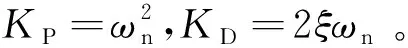
在实际当中，卫星位移与参考质量位移可通过GPS卫星获取，相对位移可以通过内部的电容传感器得到，但是相对速度无法测得，可以通过二阶插值型求导公式求得：

(14)

由以上分析根据可用量现在可列出控制律方程：

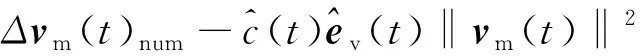
(15)

适应增益Γ由系统自身迭代得到，二阶增益γ选择下式的下限:

(16)

在建立模型仿真时，取N方向推力分辨率为1 μN，T主推力方向分辨率100 μN，W方向推力分辨率10 μN。

2 基于遗传算法的无拖曳控制器参数优化

2.1 遗传算法简介

遗传算法(genetic algorithm)[8]遵循“适者生存”、“ 优胜劣汰”的原则，是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。在每次迭代中都保留一组候选个体，重复此过程，种群经过若干代进化后，理想情况下其适应度达到近似最优的状态。遗传算法是对整个集体开始搜索，而不是针对单一的个体。

2.2 编码与解码

采用二进制编码对函数进行求解，使KP和KD保留小数点后4位，划定初始范围为[0 4]，则需要将解划分为40 000个单位，即需要16位二进制来代表这些解。一开始这些二进制串是随机产生的，在一定的迭代之后恢复至十进制表示。

2.3 适应度函数和遗传进化

适应度函数评价了遗传算法中个体的好坏。在本文中使卫星和检测质量之间的位移误差最小，选取单次迭代产生的所有位移误差的均方差作为目标函数。

初始值并不一定哪个优秀，需要通过不断的进化，淘汰差的个体保留相对优秀的个体，并在优秀的个体之间进行交叉，有些个体还会发生变异。种群的每一次进化都会产生最优个体，所有世代的最优个体就是需要的最终最优解。

进化过程包括选择、交叉、变异3个操作[9]。选择操作是从前代种群中选择个体到下一代种群的过程。选择操作前，将种群中个体按照适应度从小到大进行排列，然后采用轮盘赌的方法进行选择，适应度越高被选中的可能性越大。交叉操作是母代编码按照交叉概率交换部分编码数字。变异操作是编码串按照变异概率进行的变异。

遗传算法认为交叉操作很有可能产生优秀的个体，变异操作产生优秀个体的概率极低，但不能排除这种可能性。在仿真操作时可以设置两种操作的概率，在本次仿真时设定交叉概率为0.6，变异概率为0.01。

在进行选择、交叉和变异操作后要对产生的新的个体进行检验是否超出可测量的范围，若没有超出则继续进行循环，进行适应度排序。

在最开始进行遗传算法优化的时候设定了最大迭代次数，到达最大次数后会停止迭代，输出最终结果。

2.4 遗传算法的优化流程

由以上分析可画出遗传算法的流程，如图3所示。

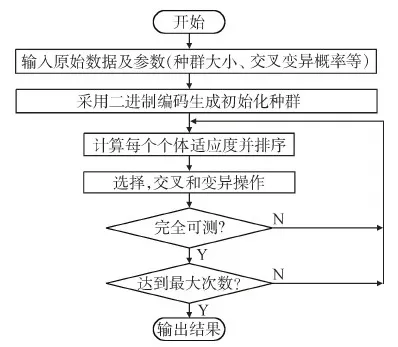
图3 遗传算法流程Fig.3 Genetic algorithm flow chart

3 无拖曳控制仿真结果分析

3.1 无拖曳控制模型推力分析

这里将分析模型的推力，并对加入遗传算法前后的推力值进行对比。

(1)加入遗传算法前的推力分析

图4为在250 km轨道运动一个周期所输出的NTW坐标系下的推力变化。由图4可以看出，无拖曳控制系统输出的最大推力是在卫星的运动方向，推力范围是5.6～11.0 mN。针对该无拖曳任务所研制的会切场推力器所要求覆盖的推力范围是 1～15 mN，避免了推力指令超出范围，使参考质量与防护罩碰撞，从而使控制器失控的现象。

理论上N方向的推力应该为0，并且应该由于初始的位移差推力在0附近波动。而W方向的推力一个周期内变动两次(-0.49～0.69 mN)，并且正方向推力较大，这是由于地球自转引起的大气旋转相对于卫星有一定的速度，因此在由北向南运动过程中需要施加一个使轨道偏向于赤道的力抵消，在由南向北的运动过程中需要施加一个使轨道偏向于极地的力来抵消掉。

图5为在250 km轨道运动一个周期所受到的NTW坐标系下的阻力变化。图6为NTW坐标系下3个方向上的推力阻力和。

加入推力对阻力进行修正后的3个方向的力大小如表1所示。在主推力方向和W方向卫星受到的力已经大大减小。N方向变化不大，但是N方向的力相对另外两个方向较小，可以接受。

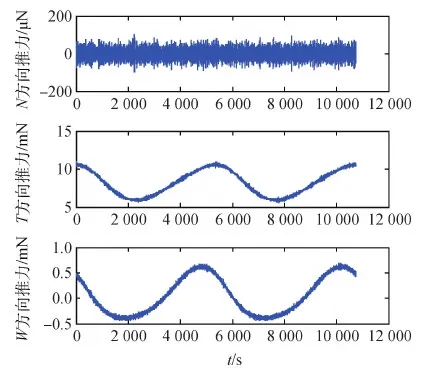
图4 NTW坐标中3个方向的推力值Fig.4 NTW coordinates in three directions thrust value

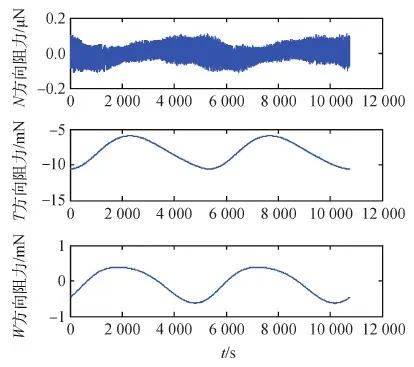
图5 NTW坐标中3个方向的阻力值Fig.5 NTW coordinates in three directions of the resistance value

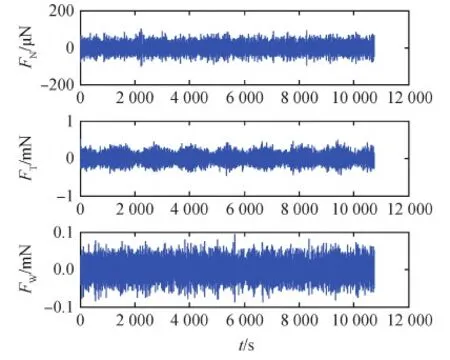
图6 NTW坐标中3个方向的推力阻力和Fig.6 Sum of thrust and resistance in three directions of NTW coordinates

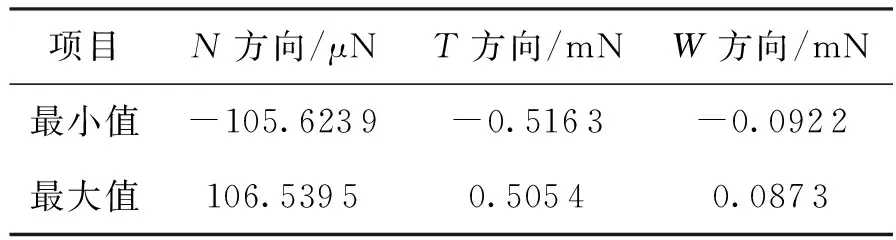
项目N方向/μNT方向/mNW方向/mN最小值-105.6239-0.5163-0.0922最大值106.53950.50540.0873

(2)加入遗传算法优化后的推力分析

加入遗传算法后的结果如图7～图9所示。

将两组波形进行对比，推力和推力阻力和均有较大提升。

可通过推力阻力和在3个方向上的极大值来对比加入遗传算法前后的变化，如表2所示。

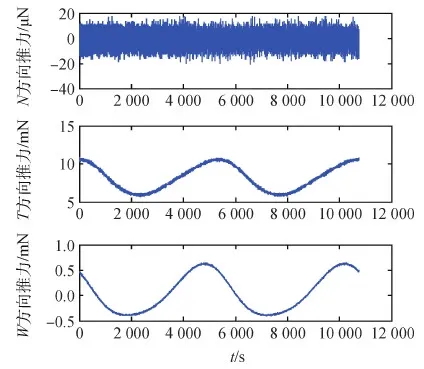
图7 加入遗传算法后NTW坐标中3个方向的推力值Fig.7 Thrust values of NTW coordinates in three directions after adding genetic algorithm

图8 加入遗传算法后NTW坐标中3个方向的阻力值Fig.8 NTW coordinates in three directions of the resistance value after adding genetic algorithm

图9 加入遗传算法后NTW坐标中3个方向的推力阻力和Fig.9 Sum of thrust and resistance in three directions of NTW coordinates after adding genetic algorithm

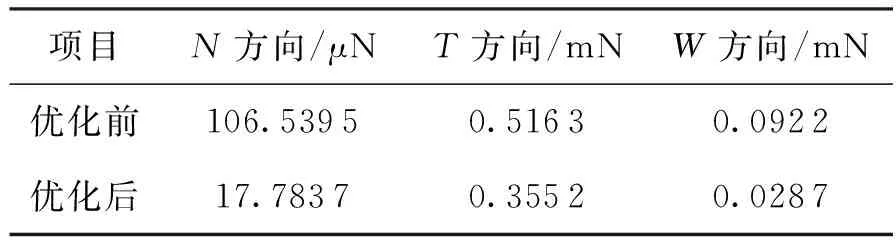
项目N方向/μNT方向/mNW方向/mN优化前106.53950.51630.0922优化后17.78370.35520.0287

由表2可以看出优化后的推力阻力和在N和W方向上有了较大的提升，T方向有大幅度的提升。这表明加入遗传算法优化后推力可以更好的抵消阻力的影响。

3.2 无拖曳控制模型的误差分析

这里将对无拖曳模型的阻力以及速度和位移误差进行分析，并将加入遗传算法前后的结果进行对比。

(1)加入遗传算法前的误差分析

在卫星运动方向上控制律估算的阻力系数和实际阻力系数随轨道周期的变化及二者的系数差比值比如图10所示。由图可看出阻力系数估计值和理论值趋势一致，阻力系数差最大值仅为0.049 6%，差值相当小。

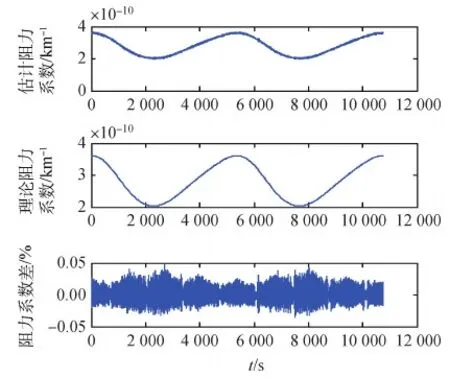
图10 阻力系数估计值和理论值及差值Fig.10 Resistance coefficient estimates and theoretical values and their Differences

图11和图12分别显示了卫星和参考质量之间的位移和速度误差，两种误差的量级在N方向和W方向上都是几十纳米，在主推力方向上是几百纳米(误差的极大值如表3所示)，均是较高的控制精度，误差都是在0附近往复波动，是控制器控制推力的结果。主推力方向上量级较大，主要是由于密度的迅速变化引起推力的变化，而推力器由于分辨率限制不能及时反映这种变化引起的，运动方向上在地球两极和赤道上存在位移和速度误差的极小值。

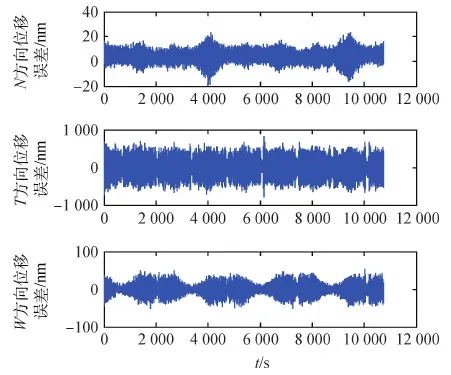
图11 NTW坐标系下3个方向的位移误差Fig.11 State errors in the three directions of the NTW coordinate system

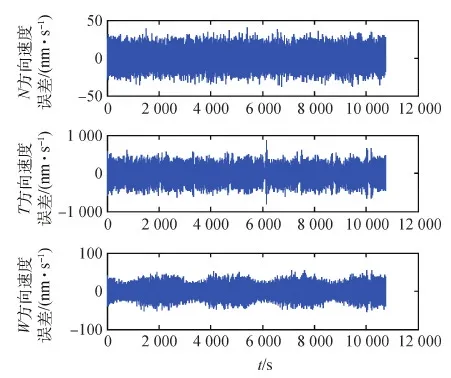
图12 NTW坐标系下3个方向的速度误差Fig.12 Velocity errors in the three directions of the NTW coordinate system

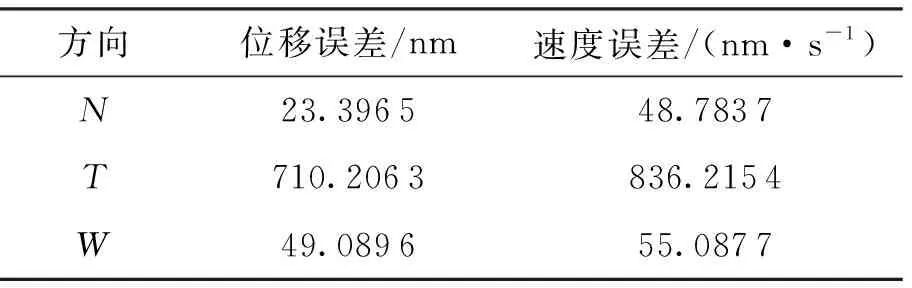
方向位移误差/nm速度误差/(nm·s-1)N23.396548.7837T710.2063836.2154W49.089655.0877

(2)加入遗传算法后的误差分析

加入遗传算法后的误差分析如图13～图15所示。

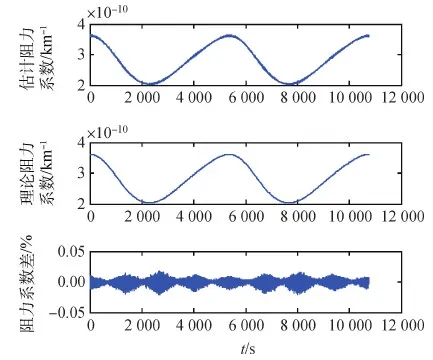
图13 加入遗传算法后阻力系数估计值和理论值及差值Fig.13 Resistance coefficient estimates and theoretical values and their differences after adding genetic algorithm

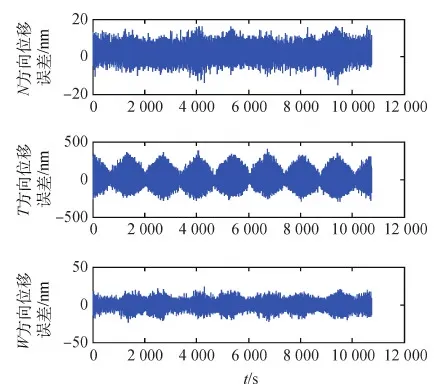
图14 加入遗传算法后3个方向的位移误差Fig.14 State errors in the three directions of the NTW coordinate system after adding genetic algorithm

在可以满足其精度的基础上加入的遗传算法优化后得到这些结果。优化后阻力系数差极大值为0.027 4%，相对优化前的0.049 6%已经有了较大的提升。

由表4、表5可以看出加入遗传算法后的位移和速度误差极大值均有所改善，但是在速度误差方面N方向没有什么变化，但是整体上可以更好的满足无拖曳控制精度。

3.3 PID参数优化对无拖曳控制系统影响

在第2节得到的无拖曳控制系统模型，采用了简单的KP和KD估计值 ，仅仅是猜测值，具有一定的鲁棒性。但是只能适用于满足经验公式条件的对象 ,只利用了较少的系统动态特性信息 , 所以得到的控制器性能也是很局限的。在使用遗传算法优化之前的KP=0.476 1，KD=0.966 0。遗传算法优化后的KP=0.876 3，KD=1.542 3。

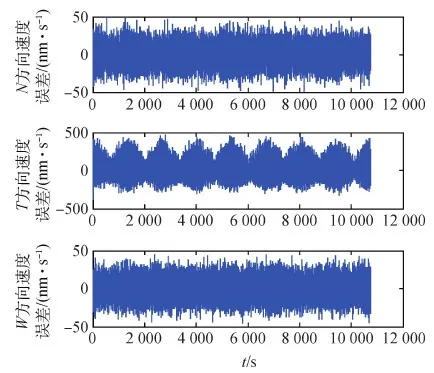
图15 加入遗传算法后3个方向的速度误差Fig.15 Velocity errors in the three directions of the NTW coordinate system after adding genetic algorithm

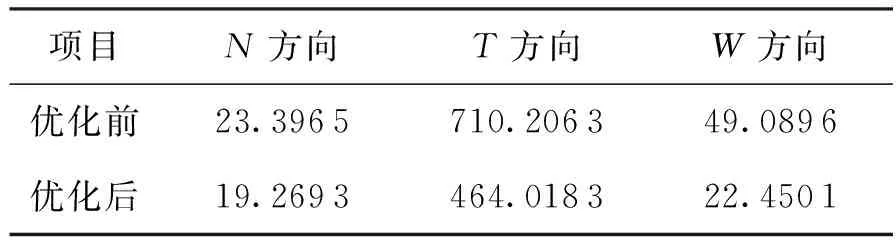
表4 加入遗传算法前后位移误差极大值

表5加入遗传算法前后速度误差极大值

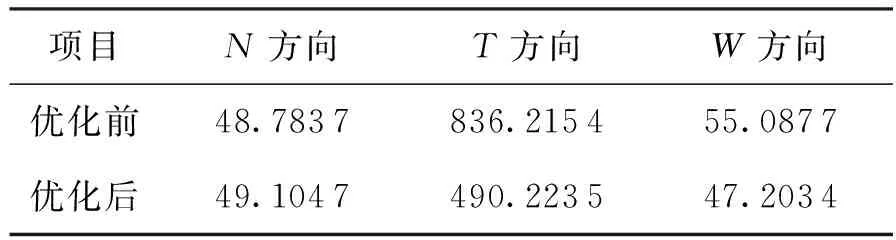
Table 5 The maximum of the velocity errors before and after adding genetic algorithm nm/s

控制系统框图如图16所示。

PID控制中P为比例部分，在本模型中对于控制系统，当传感器将航天器轨迹传递至检测质量轨迹处求差，得到两者之间的误差值。比例控制将误差等比例的传递给控制器进行相应大小的推力调节。优化前的KP参数过小，使调节的力度过小，不能很好的改正误差，系统输出量变化缓慢，调节所需的总时间过长。增大比例系数使系统反应灵敏，调节速度加快，并且可以减小稳态误差。但是过大的比例系数也会导致系统产生震荡。

D为微分部分。卫星和检测质量之间误差的微分即为误差的变化速率，误差变化越快，其微分绝对值越大。由于误差传递至航天器进行推力变换具有一定的延时，而在延时时间内比例控制对系统的改进很可能会产生超调。因此微分作用可以抵消滞后因素的影响。适当的微分控制作用可以使超调量减小，增加系统的稳定性。优化前的微分作用偏小，且现在增大了比例参数，故微分部分参数也应增大。但是微分参数过大又会使误差快速变化时，出现毛刺。

故根据遗传算法优化出合适的KP和KD使卫星和检测质量之间的误差最小。

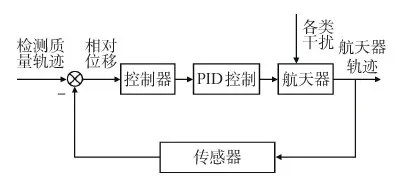
图16 无拖曳控制系统框图Fig.16 Drag-free control system block diagram

4 结束语

本文针对GOCE卫星运行过程建立了一个无拖曳控制模型，在计算精度可以保证的基础上，出于简便性考虑优先采用PID控制增强其精度，并运用遗传算法对PID参数进行优化，最终得到较为精确的结果。

无拖曳控制系统与电推力器的综合设计在GOCE卫星轨道的精确运行过程中将会起到决定性的作用。然而，目前国内并没有成功的采用电推进的重力测量卫星。将会切场推力器作为无拖曳控制系统的执行机构，不仅可以解决无拖曳飞行时宽范围、高精度的推力调节问题，还可以充分发挥会切场电推力器低腐蚀、长寿命的性能优势，为将来无拖曳卫星真正上天运行时推力器的选择有极大的参考意义。