应用分形理论研究饱和土壤渗透率
2018-11-16王在敏吴冠男
陈 卓, 王在敏, 许 模, 吴冠男
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室, 成都 610059)
0 引 言
土壤作为典型的多孔介质,其孔隙大小、毛细管弯曲性、孔隙表面形貌等都具有随机性、不规则性,但微观结构在某个或多个尺度内显示出自相似特征。因此利用分形理论刻画土壤内部结构与渗透率的联系成为研究土壤渗透率新的思路与方向。
Taylor[1]研究显示土壤孔隙形态粒径具有一定的自相似性和尺度不变性,Avnir等[2]用分子吸附技术研究岩石孔隙结构后,提出多孔介质具有分形孔隙结构,Kaze等[3-4]利用SEM对多孔的砂岩孔隙结构进行了基于分形概念的表征;Rieu等[5]借助于Sierpinski地毯图案提出了孔隙分布的分形模型。由于科技的发展,随着分形理论逐渐被引入到土壤物理学研究中,学者展开了土壤渗透率等水力特性参数与其结构之间的关系的一系列研究[6-15]。为了探究土壤体积分形维数对土壤饱和渗透率的影响,本文通过对不同配比的石英砂粒进行渗透实验求得不同配比下的砂砾渗透率,结合砂粒的体积分形维数得到了不同土壤颗粒体积分形维数的渗透率。
1 材料与方法
实验选用60、80、100目的石英砂粒通过不同质量配比5种不同的土壤试样,分别为:① 100%60目(A);② 60目∶80目=1∶1(B);③ 60目∶80目=1∶3(C);④ 100%80目(D);(5)60目∶80目∶100目=1∶1∶1(E)。实验装置示意图如图1所示,由试样筒、测压管以及供水装置组成。试样筒高60 cm、内径10 cm,试样筒上的两个出水孔由橡胶管连接到测压管上,两个出水口的位置分别位于20 cm和40 cm处。
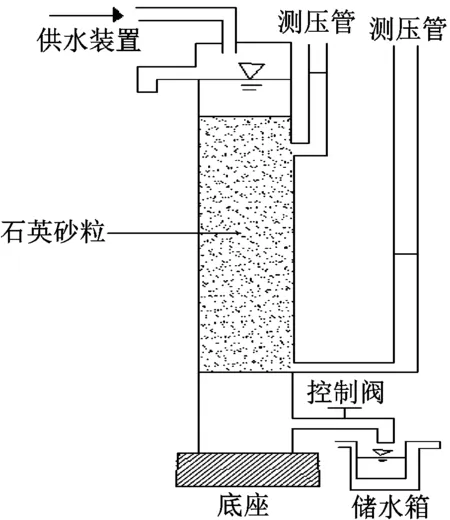
实验根据达西公式计算渗透系数:
(1)
式中:Q为渗透流量(出口处流量);A为过水断面的面积;H1、H2分别为石英砂柱两个测压管的水头;L为石英砂柱的长度;I为水力梯度;K为渗透系数。
实验测得的不同试样的渗透系数K分别为:A型1.208 mm/s,B型0.445 mm/s,C型0.206 mm/s,D型0.152 6 mm/s,E型7.737 μm/s。
2 结果与分析
2.1 土壤粒径分布的分形特征
运用激光粒度分析仪对渗流实验的石英砂粒进行颗粒粒径分析,得到5种土样的颗粒级配图,如图2所示。
太沙基认为,土壤的粒径特性主要由含量为20%的细土粒而定,即d20以下的细粒对土体性质有较大影响。谢定松等通过对粗粒土渗透系数影响因素的分析认为,控制土体渗透系数的代表性粒径应为d21。
通过对比图2中5种不同级配曲线和每种土样所对应的渗透系数,发现当小于0.1 mm细土粒所占比重增加时,土样的渗透系数相应降低,细土粒比重越大,渗透系数降低的幅度越大。但是,细土粒对于土体渗透性质的影响只能作趋势性的判断,经验性较强,没有从函数关系的角度对其进行精确刻画。
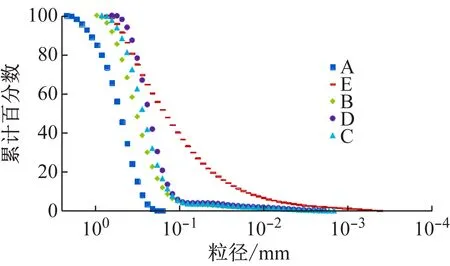
图2 不同土样颗粒级配图
随着分形理论在土壤物理学中的应用不断加深,且由于土壤颗粒粒径具有分形特征。因此运用分形维数刻画颗粒粒径分布特征成为热点。本文应用Tyler等[13]的三维体积分形维数模型计算土壤体积分形维数,
(2)
式中:V为颗粒的体积;δ为测定的尺度;di为土壤颗粒粒径;V0为土壤颗粒总体积;dmax为粒级分级中的最大粒级;D为体积分形维数。
式(2)两边同时取对数,得到体积分形维数的关系式:
(3)
根据颗粒粒径分析实验的实验数据,土壤的分级标准选用美国农业部分类系统[12],将粒径分为:极粗砂(1~2 mm)、粗砂(0.5~1 mm)、中砂(0.25~0.50 mm)、细砂(0.10~0. 25 mm)、极细砂(0.05~0.10 mm)、粉砂(0.02~0. 05 mm)和黏粒(<0.02 mm)7个等级。以lg(di/dmax)为横坐标;lg(V(δ 应用线性回结果归计算出5种土样粒径分布的分形维数D分别为:A型1.448 2,D型2.012 0,E型2.056 1,B型2.086 7,C型2.434 8。运用Excel拟合求得的体积分形维数函数关系式R2都超过90%,可信度高。发现土壤颗粒体积D的增长幅度与土壤渗透系数K的增长幅度呈正相关。 土壤颗粒体积分形维数反映颗粒粒度分布的一个特征,土壤颗粒平均粒径影响土壤颗粒体积分形维数。 根据McManus 矩算法: (a) A型 (b) B型 (c) C型 (d) D型 (e) E型 (4) 式中:MZ为颗粒平均粒径;m为颗粒粒径;f颗粒粒径所占百分比。求得MZ:A型660.780 μm,B型257.53 μm,C型213.51 μm,D型377.11 μm,E型313.04 μm。 根据MZ的数据与相应土壤的D,运用Excel进行了关系拟合,见图4。得到D数与MZ的关系式: D=-0.001 9MZ+2.711 5 (5) 据图4知,函数关系式(5)的R2为0.924 2,可信度高,表明D与MZ呈线性负相关,MZ越大,D越小。 土壤的颗粒粒径分布具有分形特征,D影响着渗透率k。对D与k的关系进行拟合,结果如图5所示。 图5 k和D的关系 根据图5得到D与其饱和时的k的对数关系式: k=0.244 lnD+0.206 9 (6) 土壤渗透系数与渗透率的关系为: K=k(ρg/μ) (7) 式中:K为渗透系数;k为渗透率;ρ为流体的密度;g为重力加速度;μ为流体的动力黏滞系数。由于实验中都是由自来水作为达西渗流实验中的流体,故常数ρ、μ是相同的,g也是相同的,因此,k与K呈正比关系,即k=nK,其中n为常数。 因此,D与其饱和时的k的关系式为: (8) 根据式(5)初步拟定D与k的对数关系通用形式为: (9) 式中:A、B为经验常数。 根据式(9)知,土壤颗粒体积分形维数与饱和土壤渗透率呈对数关系,R2达到0.952,可信度高。颗粒体积分形维数越大,土壤渗透率越小。 土壤颗粒体积分形维数取决于土样的颗粒级配曲线,对于描述土样性质具有整体意义。因此土壤颗粒体积分形维数对于土壤饱和渗透率的影响经验性质更少,具有物理意义。相对来说,以前描述颗分的参数如:标准偏差,偏度,特征粒径,不均匀系数等是从颗粒级配曲线的局部刻画其特征,具有经验性和局域性,并不具备单独描述颗分性质的能力。因此运用土壤颗粒体积分形维数能够更加全面地从土壤颗粒粒径分布角度描述土壤渗透率,且两者之间的函数关系式比较简洁,式内的参数易于求得。但是式(9)中的A、B两个参数的物理意义不明确,需要进一步探索。 本文通过渗流实验以及颗粒粒径分析实验,将土壤渗透率与颗粒粒径分形维数结合,通过数据分析得到以下结论: (2) 土壤渗透率与颗粒粒径体积分形维数关系式D=-0.001 9Mz+2.711 5,R2为0.924,可信度高。表明土壤体积分形维数与土壤颗粒平均粒径呈线性负相关,土壤颗粒平均粒径越大,土壤颗粒体积分形维数越小。 (3) 本文通过室内物理实验从土壤颗粒体积分形维数角度解释了土壤渗透率的影响因素,有望对饱和土壤渗透率进行可靠的预测。 土壤粒径分布特征对于土壤中的地下水运移尤为重要,本文通过室内物理实验,基于多孔介质分形理论对土壤体积分形维数与土壤饱和渗透率的关系进行了初步研究,由于室内实验条件的局限,不能完全模拟野外土壤的实际情况,可针对自然界实际情况进行相应的野外现场实验。自然界中的土壤多数处于非饱和状态,在非饱和状态下,土壤体积分形维数对于土壤中地下水的运移的影响有待进一步研究。随着土壤和地下水污染日益严重,掌握地下水溶质在土壤中的运移规律对于治理地下水和土壤污染尤为重要。探索土壤微观结构分形特征对于污染物迁移的影响可以成为新的研究方向。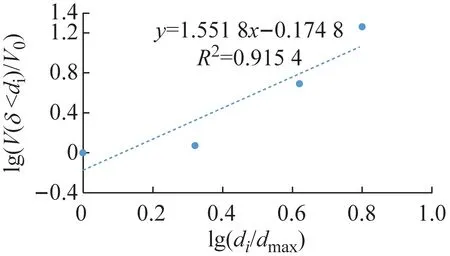
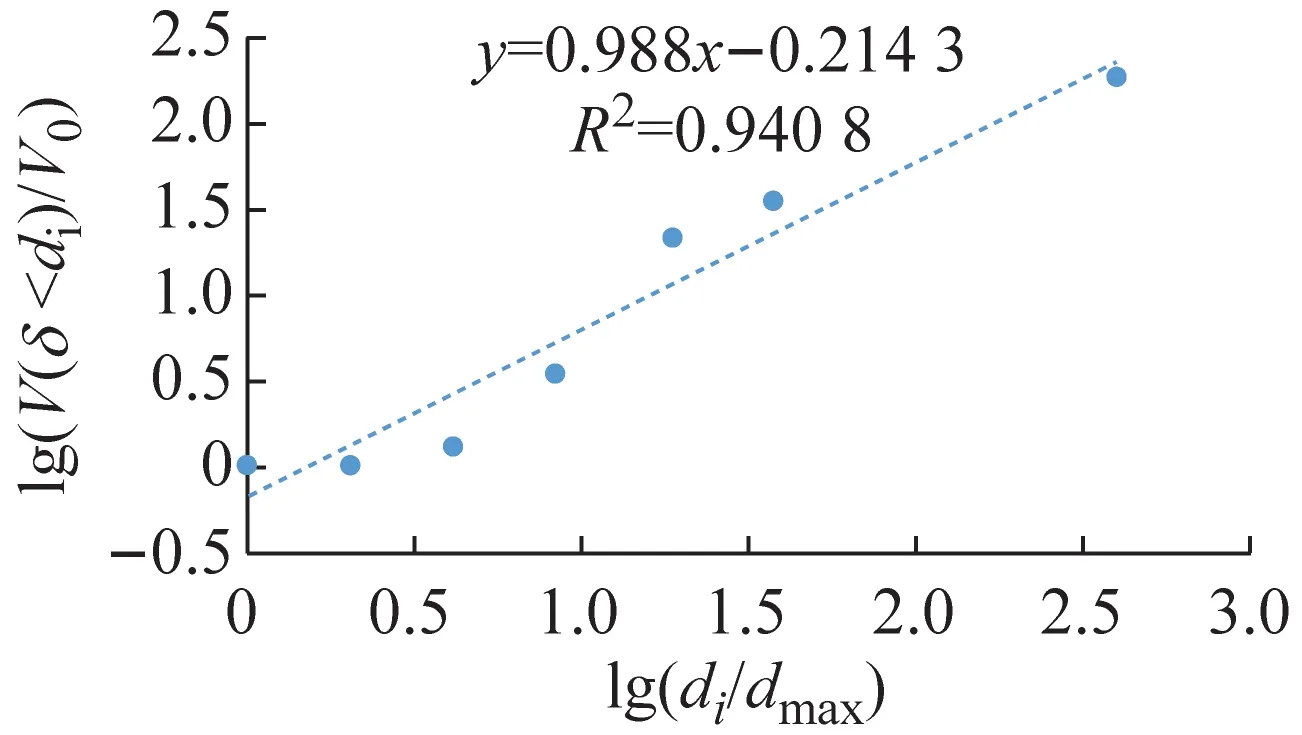
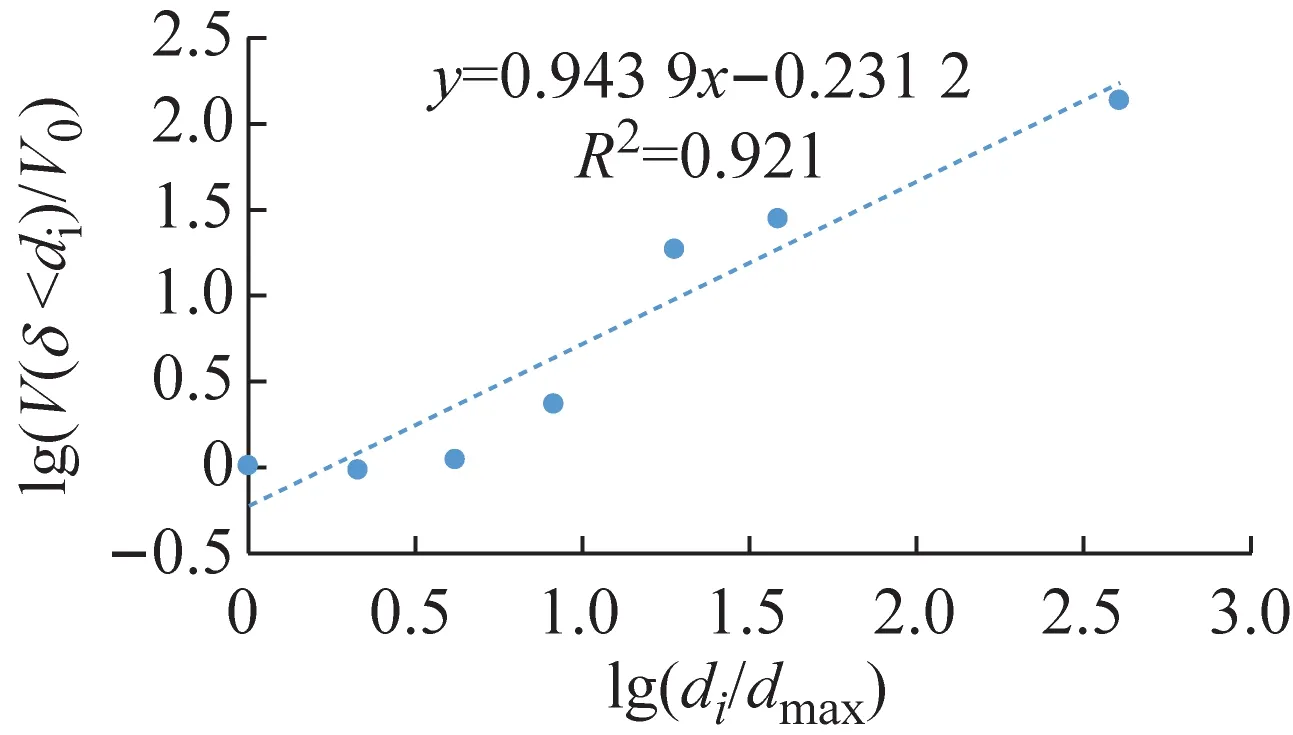
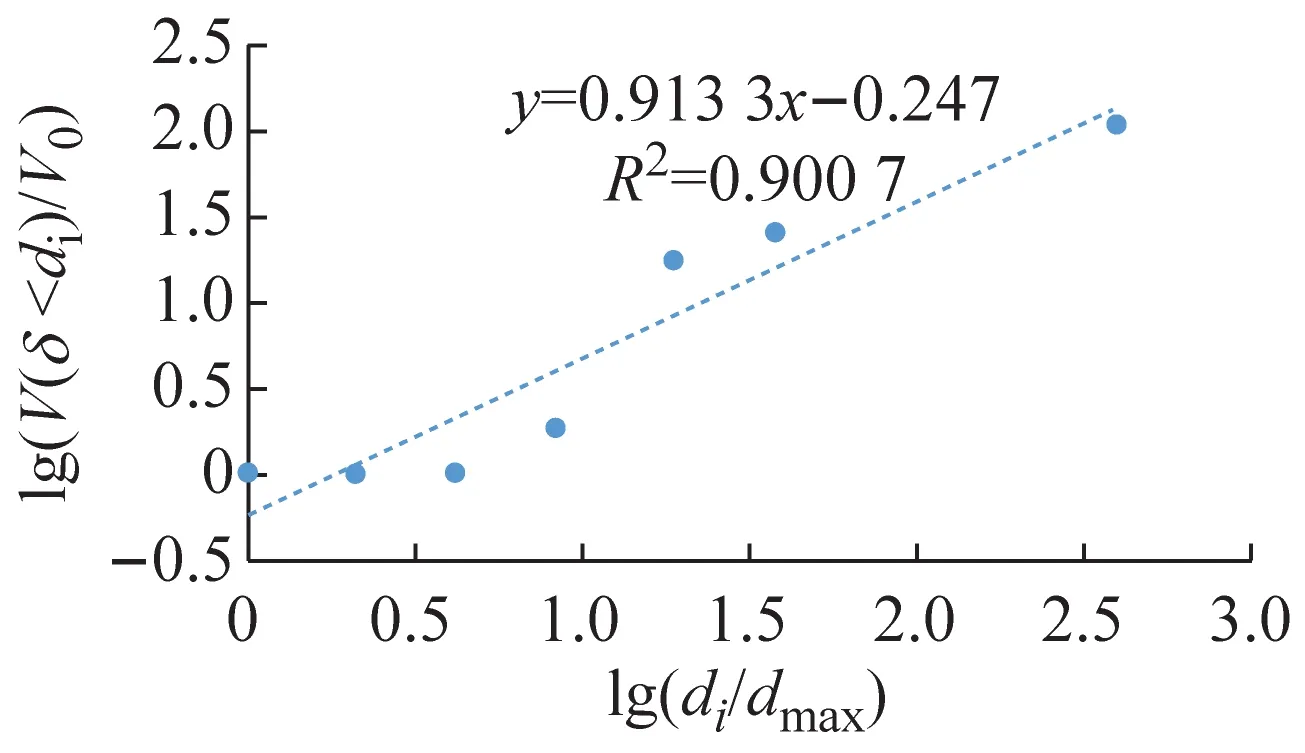
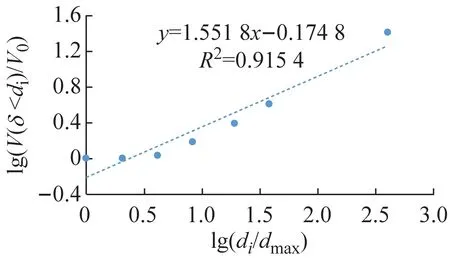
2.2 D对渗透率影响
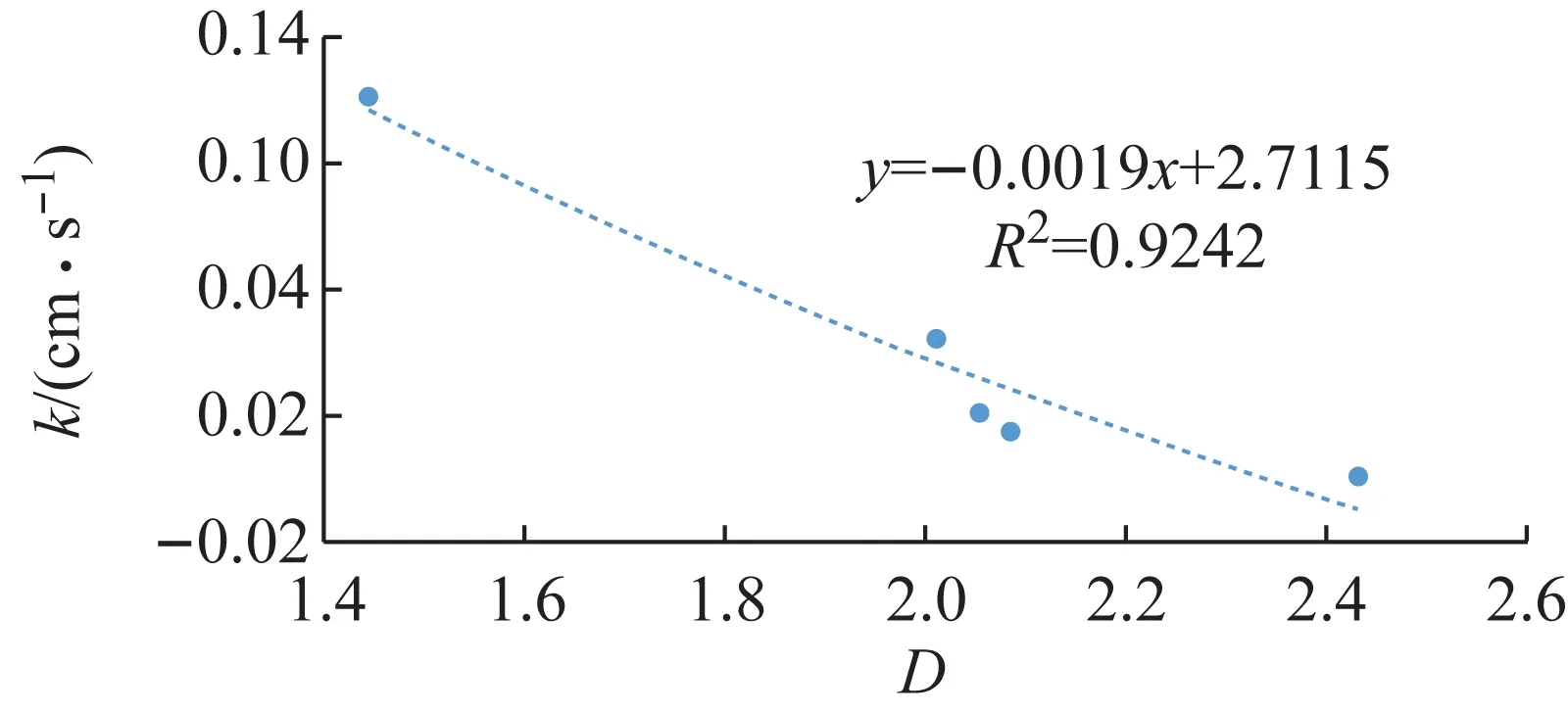
3 结 论
