六自由度串联机械臂建模与运动学分析

党浩明， 周亚丽， 张奇志

(北京信息科技大学 自动化学院，北京 100192)

0 引 言

机械臂是由一系列通过关节连接的连杆所组成的运动链。1955年，Denavit等[1]用4个参数来描述机械臂连杆坐标系，并建立了连杆坐标系间的通用变换，成为了机械臂建模和运动学描述的标准方法。

机械臂运动学研究各关节运动与机械臂末端执行器位姿之间的关系，主要包括正向运动学和逆向运动学。对于给定的一组关节角，其正向运动学解总是存在且唯一；而逆向运动学的求解则较为困难。正向运动学可以理解为从关节空间到操作空间的映射，关节空间中任一位形，在操作空间中可以找到唯一的解与之对应。而对于逆运动学，操作空间中任一位形，在关节空间中可能存在无解、唯一解或多解的情况。1961年，Pieper[2]证明了带有3个相邻关节轴交于一点的机械臂存在逆运动学解析解，为机械臂结构设计提供了理论依据，目前大多数工业机器人都具有此种构型。

针对逆运动学的求解，许多研究人员提出了不同的方法，主要包括封闭解法、数值解法和智能算法。其中，数值解法和智能算法在求解过程中不依赖于具体的机械臂结构。但数值方法[3-4]主要基于雅可比矩阵的迭代优化，在奇异点附近可能存在不稳定，不能保证算法一定收敛，且对于一组初始值只能得到一组逆解。智能算法如遗传算法[5-6]、粒子群算法[7-8]和神经网络[9-10]等，存在计算量大、局部收敛和涉及大量参数选择等问题。

封闭解法主要有几何法与代数法。其中，几何方法[11-12]适用于结构简单且自由度数较少的机械臂，对3个以上自由度的机械臂应用几何法求解逆运动学通常比较困难。代数方法依赖于特定的机械臂结构，但对于满足Pieper准则的机械臂构型，能够得到关节变量的符号表达式，故计算速度快且结果更可靠。1981年，Paul[13]提出反变换法解耦关节变量，得到了带有球形腕的斯坦福机械臂封闭解，对逆运动学代数求解具有指导作用。姜宏超等[14]采用矩阵逆乘方法得到六自由度机械臂的完整解析解。李宪华等[15]针对后3个关节轴交于一点的模块化机械臂，运用几何法和反变换法分组求得逆运动学解析解。崔玉洁等[16]对前3个关节轴交于一点的六自由度臂采用变量分离法得到逆运动学封闭解。

本文针对前三轴交于一点的六自由度机械臂，首先利用标准DH法建立机械臂的数学模型，进而得到正向运动学解。根据机械臂的构型特点，采用逆向解耦方法，利用末端位置求出机械臂后3个关节变量的值，利用末端朝向和已知关节角求出前3个关节变量的值，得到机械臂在非奇异状态下的8组解析解。并通过在齐次矩阵相乘过程中设置中间变量以及利用旋转矩阵的正交性，得到正逆运动学的快速求解算法。最后，通过对正逆运动学算法的仿真和机械臂可达工作空间的分析，证明了所提运动学算法的有效性和此种构型机械臂的实用性。

1 机械臂建模

本文以实验室自主研发的六自由度串联机械臂为研究对象，机械臂主要由6个模块化旋转关节、中间连接件和末端夹持器组成，相邻关节的关节轴相互垂直，如图1所示。

采用标准DH法建立连杆坐标系。为简化机械臂数学模型，将世界坐标系{B}固定在两肩连线的中点上，坐标系{0}和坐标系{1}、{2}固定在肩部，坐标系{3}、{4}固定在肘部，坐标系{5}、{6}固定在腕部，工具坐标系{7}固定在末端夹持器的中心。机械臂3D模型和连杆坐标系分布如图2所示，DH参数如表1所示。其中：d0=0.262 m为机械臂肩部长度；d3=0.244 5 m；d5=0.274 m分别为机械臂上臂和前臂长度；d7=0.331 5 m为末端夹持器长度。

图1 串联机械臂实物图

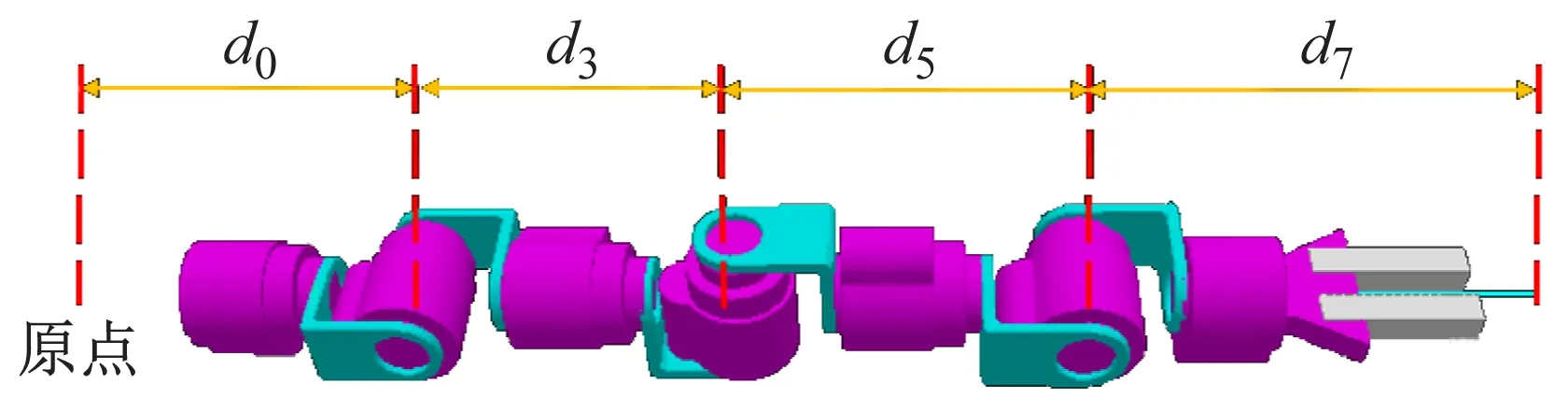
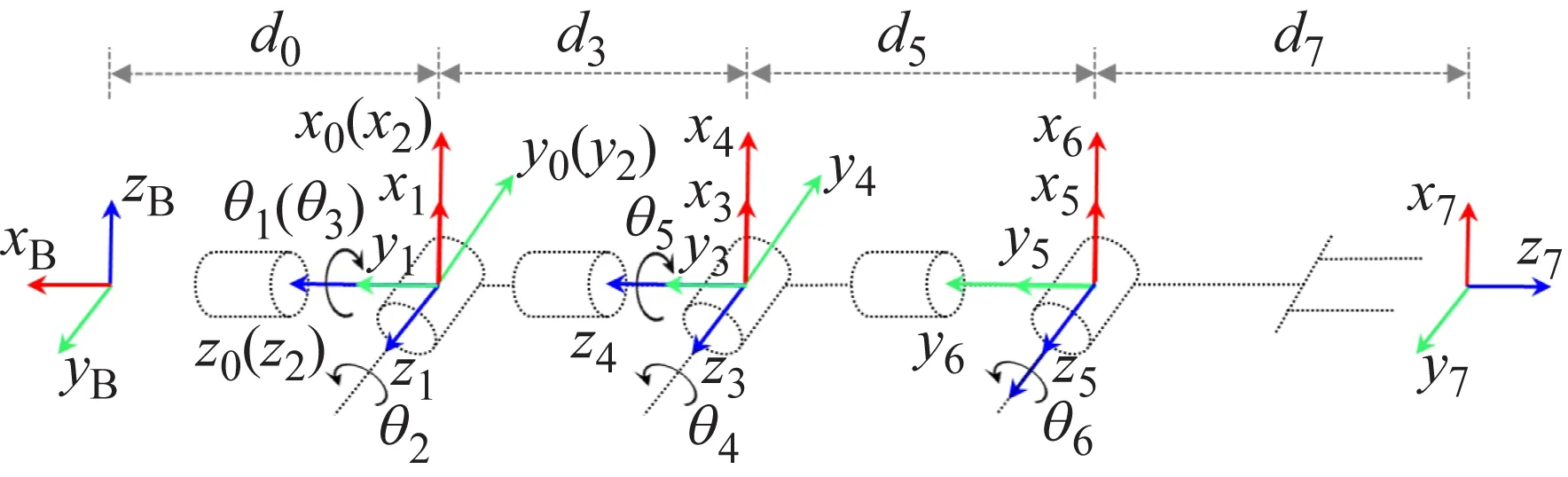
图2 机械臂3D模型和连杆坐标系分布

连杆αi/(°)aidiθi关节范围/(°)1 9000θ1(-180,180]2-9000θ2[-90,90]3 900-d3θ3(-180,180]4-9000θ4[-120,120]5 900-d5θ5(-180,180]6000θ6[-120,120]

2 正向运动学求解

由机械臂DH参数可以得到连杆坐标系{i}相对于坐标系{i-1}的变换矩阵：

trans(xi,ai)rot(xi,αi)=

(1)

将表1中的各连杆参数代入可得：

(2)

式中：ci代表cosθi；si代表sinθi。

由变换矩阵定义可知，坐标系{0}相对于世界坐标系{B}的变换矩阵和工具坐标系{7}相对于坐标系{6}的变换矩阵分别为：

(3)

通过变换矩阵连乘可以得到末端工具坐标系{7}相对于世界坐标系{B}的变换矩阵：

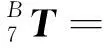
(4)

式中：[noa]和p分别代表末端工具坐标系相对世界坐标系的旋转矩阵和原点的位置向量。

注意到在矩阵相乘过程中，存在很多重复的乘积项，且计算工具坐标系{7}相对世界坐标系{B}位姿的过程中，不需要计算中间矩阵的每个元素[17]。因此，这里定义中间乘积矩阵：

(5)

用中间变量Uimn代替矩阵Ui中第m行第n列的乘积项或多项式，由式(4)和(5)可以得到末端执行器期望位姿：

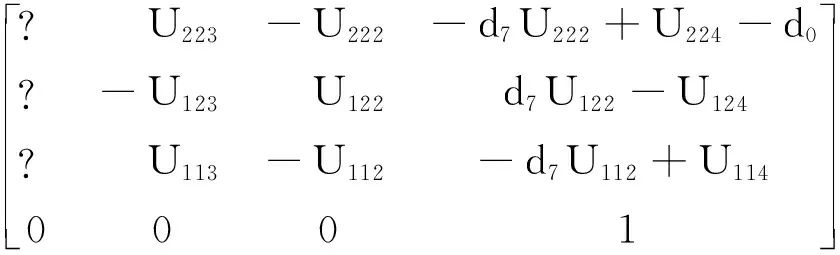
(6)

式中：?代表不需要直接计算出的项。旋转矩阵的第1列可以由第2和第3列的叉积得到：

a=n×o

(7)

计算工具坐标系位姿的过程中所需的中间变量如下：

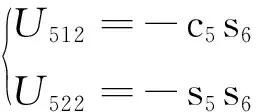
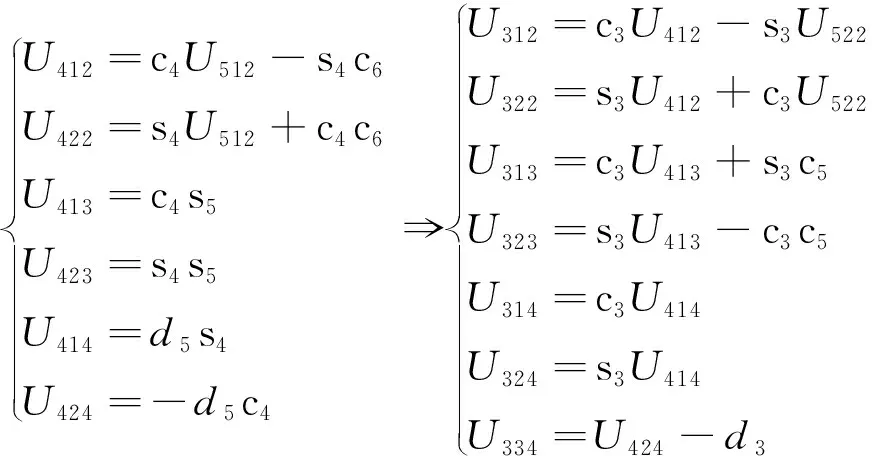
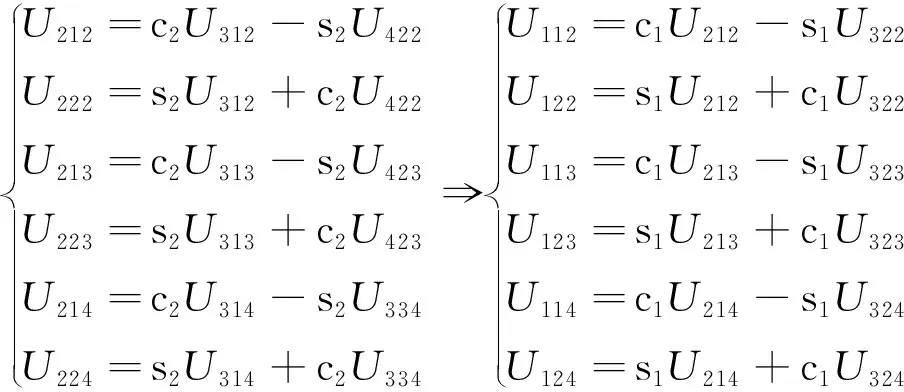
(8)

3 逆向运动学求解

对机械臂进行控制时，通常对逆运动学更感兴趣，即已知机械臂的连杆参数，给定末端工具坐标系的期望位置和姿态，找到相应的关节变量，使末端工具坐标系能够到达期望位姿。

本文所研究的机械臂前3个关节轴交于一点，满足Pieper准则，因此逆运动学解析解存在。逆运动学求解思路如下：首先，将关节变量逆向解耦为后3个关节变量和前3个关节变量。然后，利用末端位置求出后3个关节变量的值，利用末端朝向和已知关节角求出前3个关节变量的值，即可得到机械臂的8组完整解析解。

3.1 求解后3个关节变量

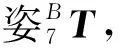
(9)

进而可以计算得到坐标系{0}的原点在坐标系{7}下的位置向量：

(10)

式中

(11)

已知坐标系{0}和{2}的原点重合，可以建立向量7P0ORG关于后3个关节变量θ4,θ5,θ6的方程：

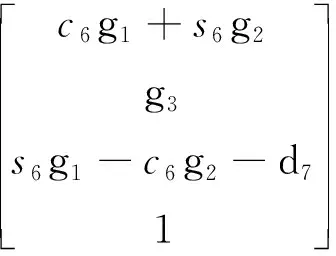
(12)

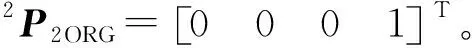
分别对式(10)和(12)的右边取平方和，可以得到：

(13)

当θ4≠0时，求得θ4的两种可能取值：

(14)

根据式(10)和(12)右边的第2个元素相等可以得到：

(15)

求得θ5的两种可能取值：

(16)

根据式(10)和(12)右边的第1个和第3个元素相等可得：

(17)

3.2 求解前3个关节变量

已知关节角θ4、θ5和θ6，可以得到：

(18)

式中，Uimn可以通过矩阵相乘代入关节变量θ4、θ5和θ6求得，需要计算的中间变量如下：

(19)

又因为

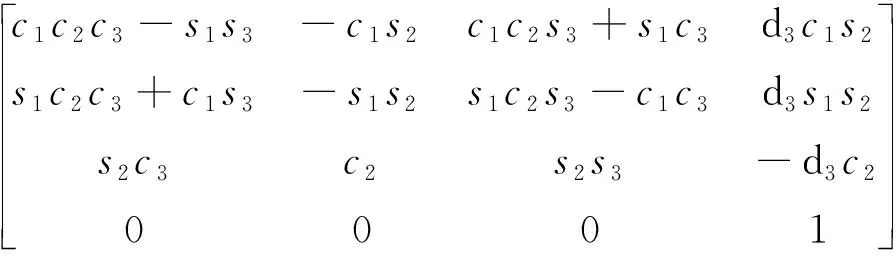
(20)

令式(18)和(20)右边的元素(3, 2)相等，可得：

c2=nxU421-axU422+oxU423

(21)

当θ2≠0时，求得θ2的两种可能取值：

(22)

令式(18)和(20)右边的元素(2, 2)和元素(1, 2)分别相等，可得：

(23)

令式(18)和(20)右边的元素(3, 3)和元素(3, 1)分别相等，可得:

(24)

以上是非奇异状态下机械臂的8组逆运动学解析解。由关节范围可知，θ2和θ4不可能等于π，则奇异位形有以下3种情况：当θ4=0时，此时只能求出关节变量θ3与θ5的和；当θ2=0时，此时只能求出关节变量θ1与θ3的和；当θ2=0且θ4=0时，此时只能求出关节变量θ1、θ3与θ5的和。当机械臂处于奇异位形时，逆运动学存在无数组解。

4 仿真验证

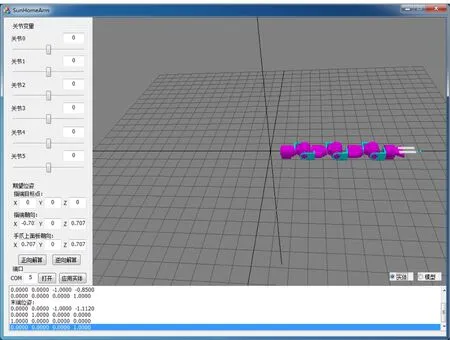
为验证正逆运动学算法的有效性，在Windows系统下基于VC++和OpenGL对机械臂进行了可视化仿真。仿真的硬件环境为：Intel Core i5-8250U处理器，主频1.6 GHz，8 GB内存。

4.1 正向运动学仿真

给定关节向量的初始位形qv=[0° -90° 0° 0° 0° 0°]T，此时机械臂应处于垂直向下的状态。给定关节向量的水平位形qh=[0° 0° 0° 0° 0° 0°]T，此时机械臂应处于水平伸展状态。当关节向量等于qv时，根据正运动学求解算法可以得到末端位姿：

当关节向量等于qh时，根据正运动学求解算法可以得到末端位姿：

机械臂仿真结果如图3所示，正运动学结果符合机械臂实际运动规律，验证了正向运动学算法的有效性。

(a) 竖直状态

(b) 水平状态

4.2 逆向运动学解仿真

给定末端期望位姿矩阵，对得到的8组逆解分别应用正向运动学，得到8个末端执行器位姿矩阵，分别计算它们与期望位姿之间的误差，若误差满足控制精度要求，则说明逆运动学算法有效。

在关节范围内给定任意一个的关节向量，例如q0=[30° 40° 50° 60° 70° 80°]T，根据正向运动学算法可以得到期望位姿：

将变换矩阵应用于逆向运动学算法可以得到8组逆运动学解如表2所示，结果保留2位小数。

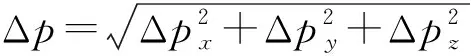
由仿真结果可知，逆运动学算法求得的8组解对应机械臂同一末端期望位姿，其位姿误差主要由舍入误差引起，能够满足机械臂控制的精度要求，且8组逆解中包含初始关节向量q0，验证了逆运动学算法的有效性和完备性。

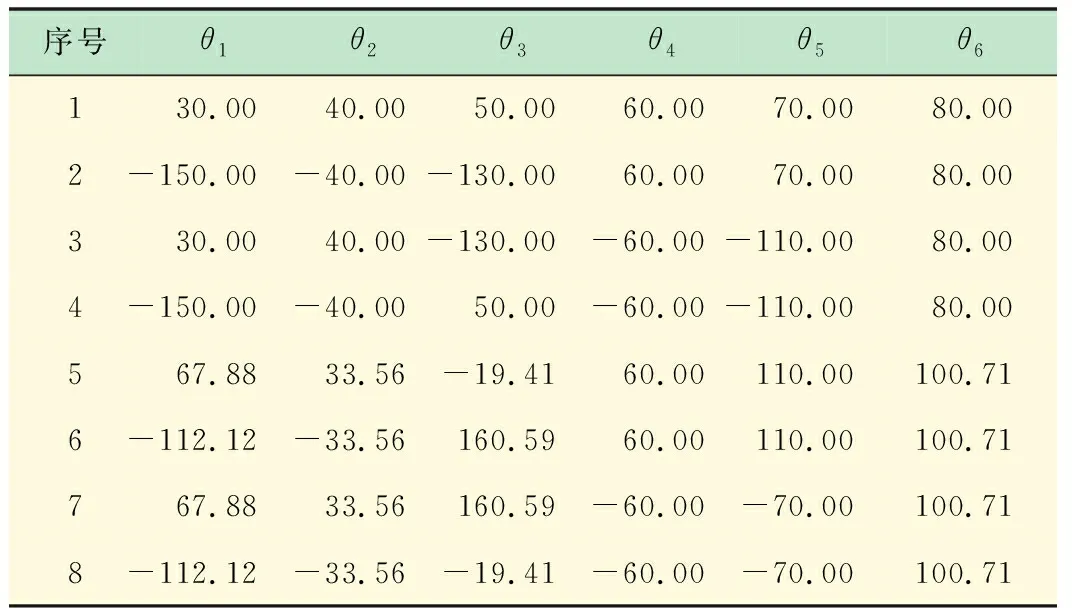
表2 8组逆运动学解 (°)

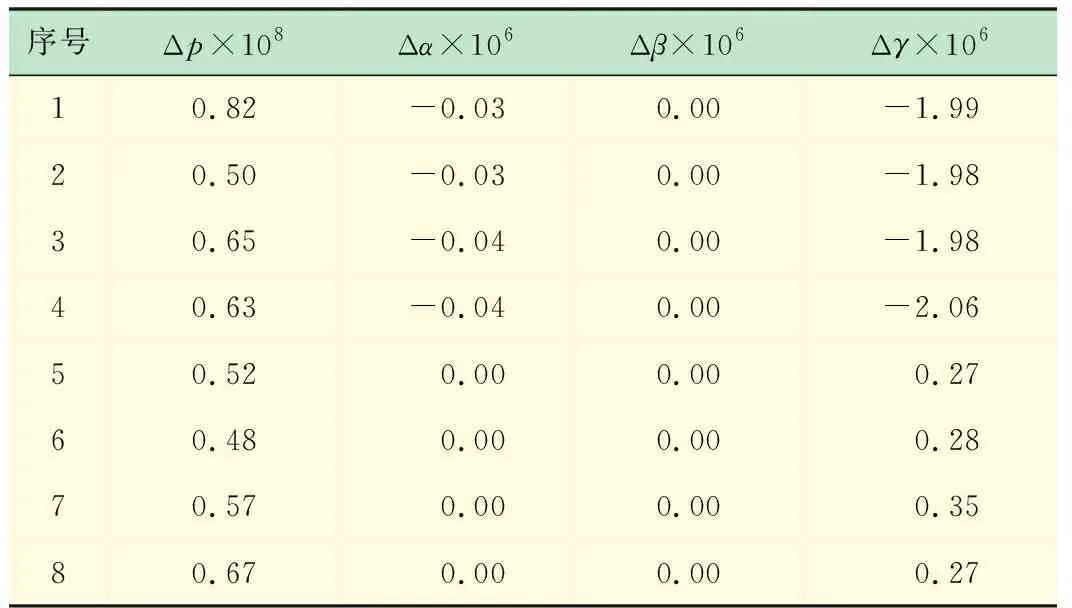
表3 8组逆运动学解的位姿误差

分别运用矩阵连乘方法和设置中间变量的方法求解正逆运动学，在C++环境下对比两种方法的平均计算时间，如图4所示。由图中可以看出，通过设置中间变量的方法，能够显著减少算法运算量，缩短程序运行时间。正向运动学的平均运算时间约缩短为原来的44.87%，逆向运动学的平均运算时间约缩短为原来的64.00%。

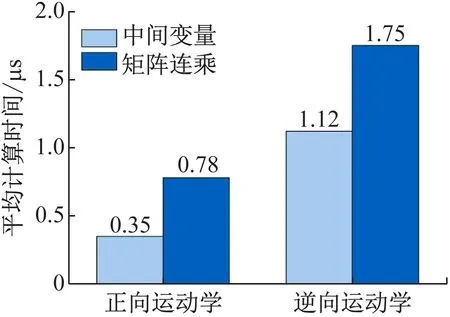
图4 运动学平均计算时间

4.3 工作空间仿真

机械臂的工作空间指操作空间中末端执行器能够到达的点的集合。工作空间是机械臂结构设计的一个重要指标，分析其特点对研究机械臂的性能及障碍物回避等有着实际意义。

生成工作空间的方法主要包括解析法和数值法。其中，数值法更加简单且灵活，不依赖于具体的机械臂结构，能够得到工作空间的近似边界曲面。蒙特卡洛法基于随机理论，是求解工作空间的常用方法。其基本思想是，所有关节变量在取值范围内遍历取值后，末端执行器所处位置的点的集合即构成工作空间。

由表1确定的关节范围内，对每个关节变量取N=10×104个随机值，组成N个关节向量。对每个关节向量运用正运动学算法，可以得到由腕关节与末端执行器在操作空间中的位置所形成的点云，分别如图5与图6所示。

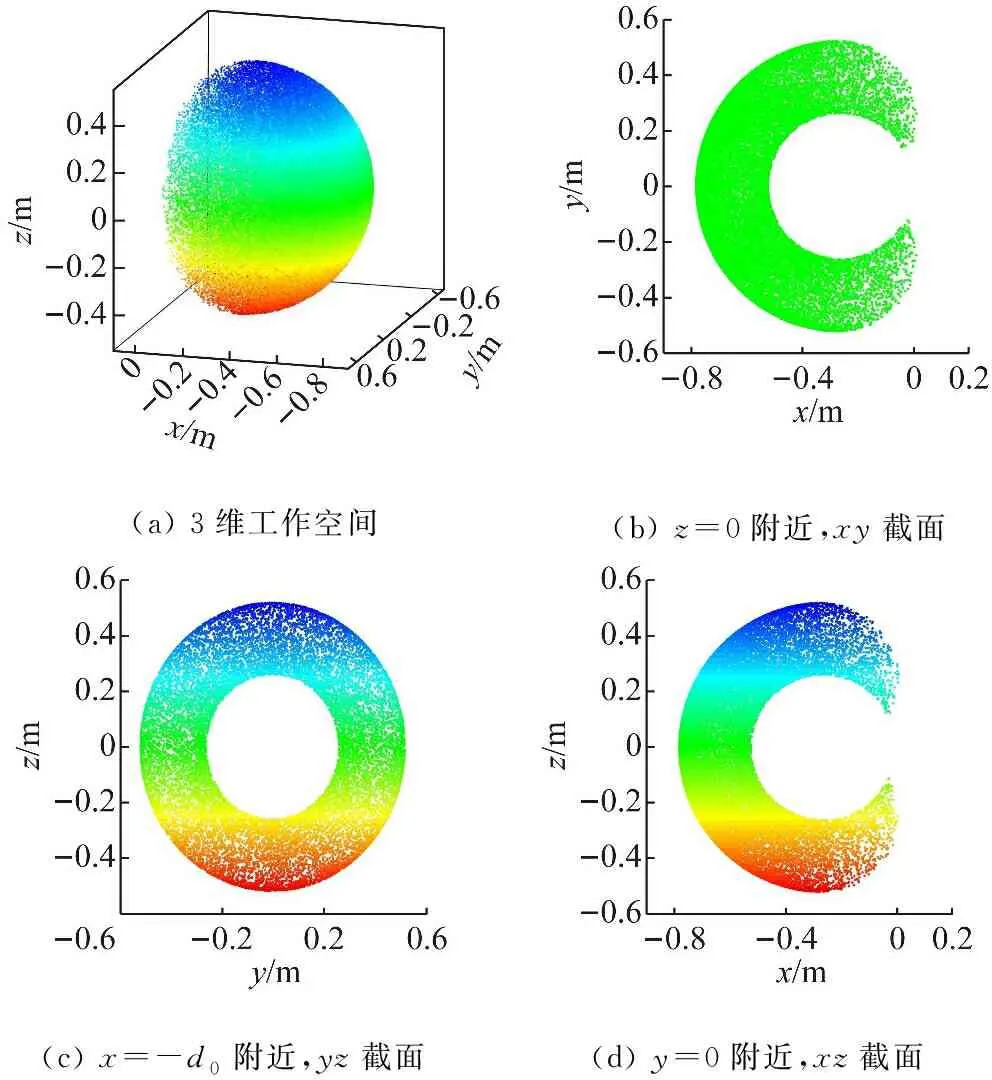
(a) 3维工作空间(b) z=0附近,xy截面(c) x=-d0附近,yz截面(d) y=0附近,xz截面

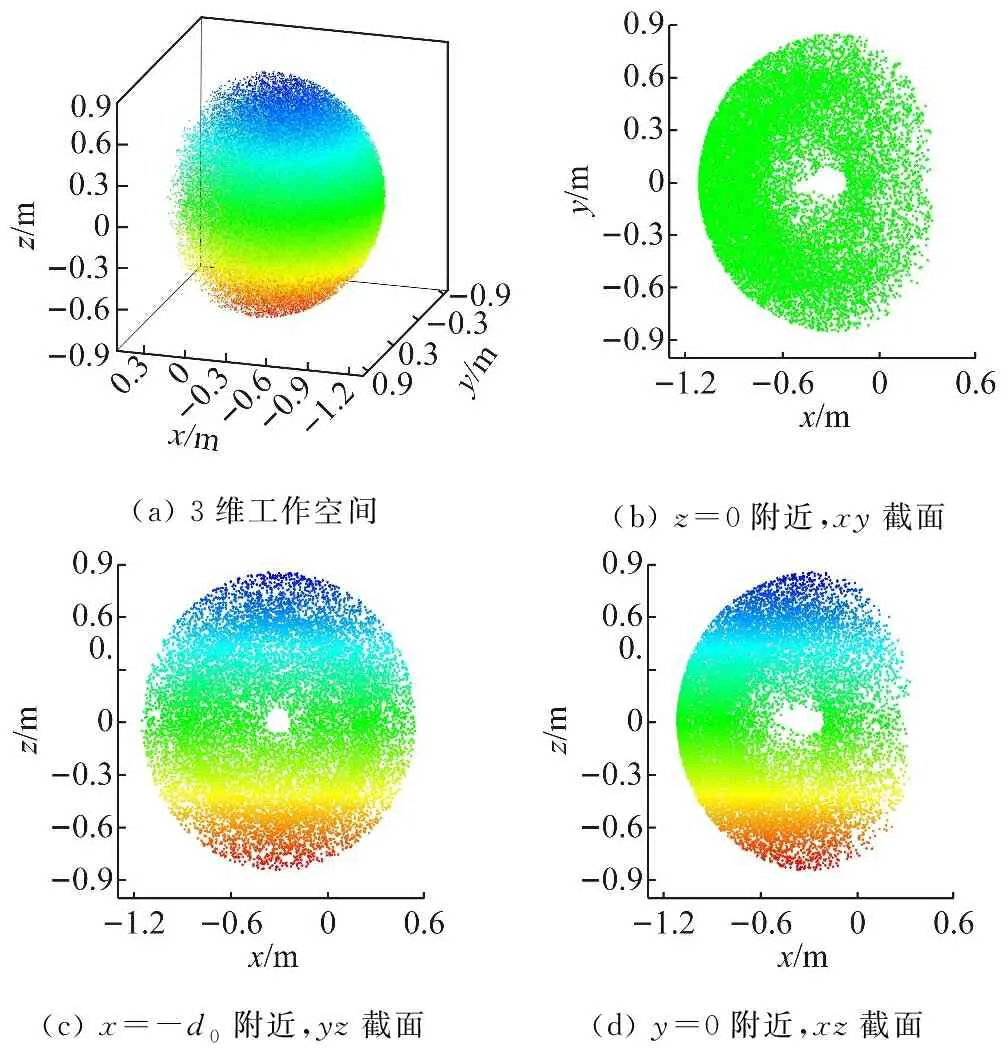
图5 腕关节工作空间点云图

图6 末端执行器工作空间点云图

可以看出，腕关节与末端执行器工作空间近似为空心的椭球体，机械臂工作空间受连杆长度和关节范围影响较大。其中，腕关节工作空间沿x轴的移动范围约为[-0.780 5 m, -0.011 2 m]，沿y轴和z轴的移动范围为[-0.518 5 m, -0.518 5 m]。末端执行器工作空间沿x轴的移动范围约为[-1.112 0 m, 0.340 7 m]，沿y轴和z轴的移动范围为[-0.85 m, -0.85 m]。

5 结 语

针对自主研发的六自由度串联机械臂进行了DH建模，并根据机械臂的构型特点，得到其正向运动学解和逆向运动学8组完整解析解。在运动学求解过程中，利用齐次矩阵连乘时存在重复乘积项的特点，定义中间变量得到了正逆运动学的快速求解算法。最后对所提算法和机械臂的工作空间进行了仿真实验，验证了正逆运动学算法的正确性和高效性，该建模和运动学求解算法也可应用于具有相似结构的机械臂。