斜风下大跨度悬索桥三维非线性静风稳定性研究
2021-11-30张新军李寒妍余天程
张新军,李寒妍,余天程
(1.浙江工业大学 土木工程学院,浙江 杭州 310023;2.浙江省工程结构与防灾减灾技术研究重点实验室,浙江 杭州 310023)
悬索桥结构受力性能好,跨越能力强,是当前主跨超千米桥梁的主要结构形式。为适应未来跨海连岛工程的桥梁建设需要,悬索桥潜在的跨径需求为2 000~5 000 m[1]。悬索桥跨度大,结构刚度小,静风稳定性是其设计中需要关注的重要问题。当前,大跨度悬索桥的静风分析研究主要针对法向风作用情况,即假设风的来流方向与桥轴线正交。大跨度桥梁在确定桥位时,通常使桥轴线的法向偏离桥址处的主风向,内地山区或复杂地形地区的桥梁所受的自然风方向复杂多变,沿海地区桥梁经常遭受风向多变的台风侵袭,现场风速观测表明桥梁所受强风的作用方向大多偏离桥跨法向[2]。鉴于现实情形下桥梁多承受斜风作用,因而研究斜风下悬索桥的静风稳定性以确保其安全运营具有重要的理论和工程意义。
目前,斜风下的静风分析主要采用两种方法,即平均风分解法和斜截面法。前者将斜风分解为与桥跨方向相垂直的余弦分量和与桥跨方向一致的正弦分量,分别计算两个风速分量下的结构静力反应,最后将结果进行叠加[3]。张文明等[4]结合平均风分解法提出了斜风作用下大跨度悬索桥非线性静风稳定分析方法,并对某三塔双主跨悬索桥进行了不同风偏角和风攻角组合工况的非线性静风稳定分析,发现该桥静风失稳最低临界风速出现在初始风偏角为7.5°且初始攻角为1.5°时。Zhu等[5-6]建立了桥梁结构斜风荷载响应分析的斜截面法,在风洞试验中用六分量力天平直接测量桥梁斜片条节段上的静风荷载六分力系数,并将之应用于斜风下桥梁结构的静风分析。在此基础上,丁泉顺等[3]提出了斜风作用下桥梁结构静风反应分析的简化方法,结合南京长江三桥进行成桥和施工状态的静风分析,通过与全桥气弹模型风洞试验结果的对比验证了方法的可靠性。张征文[7]基于CFD分析获得不同风偏角下苏通长江大桥主梁断面的静风三分力系数,通过坐标系变换得到法向风下的五分力系数,以此进行不同风偏角下的静风稳定性分析,发现在0°初始风攻角下静风失稳临界风速随风偏角增大而提高,但在+3°初始风攻角下静风失稳临界风速随风偏角增大呈波动变化,在5°风偏角下达到最低值。张宏杰等[8]针对主跨1 400 m斜拉桥进行了法向风和斜风下的节段模型风洞试验,发现桥梁静风失稳的最不利工况出现在风偏角较小情况下。此外,文献[9-11]通过节段模型风洞试验分别针对板桁结合加劲梁、倒梯形断面桁架梁和扁平钢箱梁开展了四分力、五分力和六风力等静风系数随风攻角和风偏角的变化规律的研究,并与传统斜风分解法所得结果进行比较,进一步说明采用斜风下节段模型试验测得的静风系数进行斜风下结构静风分析的必要性。上述研究主要针对斜风下的静风分析方法、斜拉桥静风性能以及不同主梁断面形状的静风系数等,对斜风下大跨度悬索桥的静风稳定性研究鲜有涉及。为此,基于斜风作用下静力风荷载计算模型,考虑结构和静风荷载随结构变形的双重非线性因素,笔者建立了斜风下大跨度桥梁三维非线性静风分析方法,并编制其计算程序。采用该程序,对润扬长江大桥南汊悬索桥开展斜风作用下悬索桥三维非线性静风稳定性分析,并揭示斜风作用对大跨度悬索桥静风稳定性的影响。
1 斜风下大跨度桥梁三维非线性静风分析方法及计算程序
1.1 有效风偏角和有效风攻角定义
斜风在桥梁平面的投影与桥轴线(侧弯前)法线之间的夹角称为初始风偏角β0,斜风作用下主梁侧弯,主梁上任意点产生侧弯偏角φ,即侧弯前后桥轴线法线之间的夹角,侧弯后桥轴线法线与斜风在桥梁平面的投影之间的夹角定义为有效风偏角β,β=β0+φ,如图1(a)所示。斜风与变形前主梁的平面夹角为初始风攻角α0,主梁受风荷载作用发生扭转变形,此时主梁任意点的扭转角为θ,斜风与主梁扭转后平面之间的夹角定义为有效风攻角α,α=α0+θ,如图1(b)所示。

图1 有效风偏角和有效风攻角示意图
1.2 斜风作用下结构所受的静力风荷载
在单元局部坐标系下,斜风作用下桥面主梁单位长度所受的静力风荷载Fst如图2所示。
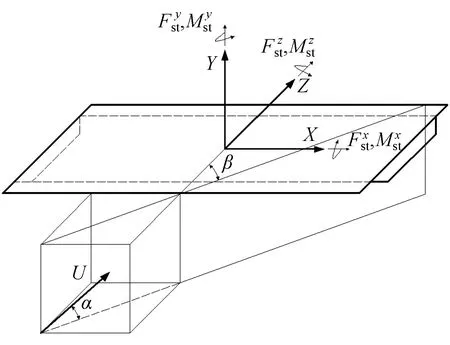
图2 斜风下主梁上的静风荷载
静力风荷载Fst计算公式为
(1)

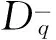

图3 斜风下缆索上的静风荷载
单位长度缆索单元受到的静风力表示为
(2)
(3)
(4)
式中:D为缆索截面直径;CD0为缆索截面法向风下的阻力系数。
1.3 斜风下结构三维非线性静风分析方法及计算程序
在斜静风作用下,结构的几何和内力状态随结构变形而改变,并导致结构刚度以及以结构变形为函数的静风荷载的三维非线性变化。因此,斜风下结构静风分析即为求解以下的几何和静风荷载双重非线性方程为
KT(δ)δ=F(δ)
(5)
式中:KT(δ)为结构切线刚度矩阵;δ为结构静风位移向量;F(δ)为作用于结构的非线性静风荷载向量。
对于式(5),可以采用UL列式法进行迭代求解,相应的迭代方程为
KT(δj-1)Δδj=Fj(αj,βj)-Fj-1(αj-1,βj-1)
δj=δj-1+Δδj
(6)
式中:KT(δj-1)为第j-1步迭代后结构的切线刚度矩阵;Δδj为第j步迭代后的结构位移增量向量;Fj(αj,βj)为第j步迭代时对应于有效风攻角αj和有效风偏角βj的结构静风荷载向量;Fj-1(αj-1,βj-1)为第j-1步迭代后对应于有效风攻角αj-1和有效风偏角βj-1的结构静风荷载向量。
式(6)迭代求解时必须确定一个合理的收敛准则,笔者采用静风系数的欧几里得范数作为收敛准则,即

(i=1,2,…,m)
(7)
式中:‖…‖2为向量的欧几里得范数;Ci(αi,βi)为第i个受静风作用单元对应于第j迭代步结束时的静风系数向量;Ci(αj-1,βj-1)为第i个受静风作用单元对应于第j-1迭代步结束时的静风系数向量;ε为迭代精度;m为受静风作用的单元个数。
基于上述理论分析并采用增量迭代方法,笔者编制斜风下大跨度桥梁三维非线性静风分析程序SNAA-SW。计算时,将风速按一定的步长增加,并适时调整步长以搜索结构的临界失稳风速,在每一级风速下通过如图(4)所示的计算流程求解结构的静风平衡状态。

图4 斜风下结构三维非线性静风分析计算流程
2 桥梁简介
润扬长江大桥南汊桥为主跨1 490 m的单孔简支钢箱梁悬索桥(以下简称为润扬悬索桥),桥跨布置为470 m+1 490 m+470 m,其总体布置如图5[12]所示。主缆采用预制平行钢丝索股,单根主缆共184 股,每股含127 根镀锌高强钢丝,主缆矢跨比为1/10,横桥向中心距为34.3 m;主跨共设91 对吊杆,纵向间距为16.1 m,吊杆与主缆和加劲梁的连接均采用销接;加劲梁为扁平状流线形钢箱梁,梁高3.0 m,总宽38.7 m。桥塔为钢筋混凝土门式框架结构,塔高约为210 m。为避免跨中短吊杆的弯折并改善结构整体受力性能,主跨中央设置缆梁固结的刚性中央扣。

图5 润扬悬索桥总体布置图
3 斜风下大跨度悬索桥静风稳定性分析
虽然润扬悬索桥未开展斜风下主梁节段模型风洞试验,但其桥面主梁截面形状和尺寸与南京长江三桥(图6)极为相似,因此以下静风分析时均采用斜风作用下南京长江三桥成桥状态主梁节段模型风洞试验测得的静风系数[13]。为了说明采用南京长江三桥静风系数分析润扬悬索桥静风性能的合理性,在0°初始风攻角和0°初始风偏角下,分别采用润扬悬索桥[14]和南京长江三桥节段模型试验测得的静风系数,运用斜风作用下大跨度桥梁三维非线性静风分析程序SNAA-SW分析润扬悬索桥成桥状态的静风稳定性,计算得到的主跨跨中处主梁的横向和竖向位移以及扭转角随风速增加的变化曲线如图7所示,图中DL,DV和DT分别表示横向和竖向位移以及扭转角,U为斜风风速。由图7可知:在0°初始风攻角的法向风作用下,采用实桥和南京长江三桥静风系数计算得到的主跨跨中处主梁位移以及随风速增加的变化趋势基本一致,达到静风失稳的临界风速也基本相同,说明南京长江三桥的静风系数能很好地反映润扬悬索桥的静风性能,分析是可信的。

图6 南京长江三桥主梁截面图(单位:cm)

图7 0°初始风攻角和风偏角下不同静风系数的主跨跨中处主梁位移—风速曲线
在0°,±1°,±2°和±3°等7 个初始风攻角下,采用斜风作用下大跨度桥梁三维非线性静风分析程序SNAA-SW开展0°,5°,10°,15°和20°这5 个初始风偏角的静风稳定性分析,因其他方向的静风位移比较小,因此仅给出各初始风攻角β0和初始风偏角β0组合下主跨跨中处主梁横向和竖向位移以及扭转角随风速增加的变化曲线,如图8所示。
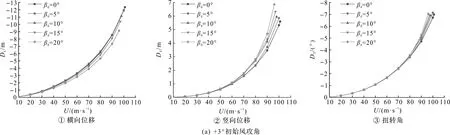
图8 不同初始风攻角和风偏角的主跨跨中处主梁位移-风速曲线
通过对图8的结果进行比较可以发现:1)斜风作用下,加劲梁的横向、竖向和扭转位移随着风速的增加逐渐增大,都呈现非线性增长规律,静风失稳形态表现为主梁横向和竖向位移以及扭转变形强烈耦合的空间失稳形态,这与法向风作用下悬索桥的静风失稳形态基本一致,说明斜风作用不会改变悬索桥的静风失稳形态;2)各初始风攻角下主梁跨中处位移随风速增加的变化曲线存在着一定差异,尤其是竖向和扭转位移,如在+1°,0°,-1°和-2°初始风攻角下当达到一定风速水平时,主梁的竖向和扭转位移会急剧增大,位移变化曲线存在明显拐点,呈现出“硬”静风失稳特点,而在其它初始风攻角下位移变化曲线则没有出现明显拐点,表现为“软”静风失稳特点;3)在同一初始风攻角下,各初始风偏角的跨中处主梁位移随风速增加的变化规律基本一致,说明风偏角对静风失稳形态影响不大,但会明显影响静风失稳的临界风速。
为了说明斜风效应对成桥状态悬索桥静风稳定性的影响,结合上述主梁位移随风速增加的变化曲线定义了静风失稳临界风速。通常情况下,以结构静风变形发散导致计算失败时对应的风速值定义为静风失稳临界风速,在有些工况下即使风速很高也不会出现计算失败,但仔细观察会发现主梁的有效风攻角早已超出了静风系数的试验风攻角范围,计算已经失真。针对这种情况,笔者将主梁单元首次出现有效攻角绝对值接近或稍微超出静风系数试验攻角范围时的风速值定义为静风失稳临界风速[4]。结合上述主梁位移随风速增加的变化曲线以及计算情况,得到如图9所示的静风失稳临界风速Ucr随风攻角和风偏角增加的变化曲线。需要说明的是:南京长江三桥主梁断面静风系数试验风攻角范围为-10°~+10°,在-2°和-3°两个初始风攻角下的静风稳定性分析时遇到了主梁有效风攻角超出试验风攻角范围的情况,故选取主梁有效风攻角绝对值首次达到10°时的风速为静风失稳临界风速。

图9 静风失稳临界风速随风偏角和风攻角增加的变化趋势
斜风效应对润扬悬索桥静风失稳临界风速的影响率见表1,影响率ηβ定义为

表1 斜风效应对静风失稳临界风速的影响率
ηβ=(Ucr,β-Ucr,0)/Ucr,0
(8)
式中:Ucr,β为斜风下的静风失稳风速;Ucr,0为法向风下的静风失稳风速。
由图9(a)可知:除-2°和-3°初始风攻角外,其余初始风攻角下的静风失稳临界风速都随着初始风偏角的增加而逐步下降,在-2°和-3°初始风攻角下,静风失稳临界风速随初始风偏角增加而逐步上升。该桥静风失稳最低临界风速出现在+3°初始风攻角的20°初始风偏角下,说明斜风对大跨度悬索桥静风稳定性可能更不利。斜风作用对悬索桥的静风稳定性的影响存在正负效应,并非如余弦法则所分析的单调增加趋势,特别要重视斜风作用的负效应。由图9(b)可知:在同一初始风偏角下,静风失稳临界风速随初始风攻角增加呈现偏态的倒U形变化规律,+3°初始风攻角下结构静风稳定性最低,其次是-3°初始风攻角,-1°初始风攻角时结构静风稳定性最好,总体上负风攻角下结构静风稳定性较好。由表1可知:随着初始风偏角的增加,斜风作用对静风失稳临界风速的影响率逐渐增大,影响幅度为-8%~6%,斜风效应影响明显,因此尤其要重视较大初始风偏角下斜风效应产生的不利影响。
4 结 论
基于斜风下结构所受的静风荷载模型,考虑静风荷载和结构的双重非线性因素,建立了斜风下大跨度桥梁三维非线性静风分析方法,并编制了相应的计算程序SNAA-SW。采用该程序,以润扬长江大桥南汊悬索桥为研究对象,进行了不同初始风攻角和初始风偏角下的静风稳定性分析,得出的主要结论如下:1)与法向风情况相似,润扬悬索桥的静风失稳形态表现为主梁空间弯扭耦合的失稳形态,说明斜风作用不会改变悬索桥的静风失稳形态;2)斜风作用对悬索桥的静风稳定性的影响存在正负效应,除-2°,-3°初始风攻角外,其余初始风攻角下静风失稳临界风速都随着初始风偏角的增加而逐步下降,该桥静风失稳最低临界风速出现在+3°初始风攻角的20°初始风偏角下,说明斜风对大跨度悬索桥静风稳定性可能更不利;3)随着风偏角的增加,斜风作用对静风失稳临界风速的影响逐渐明显,影响幅度为-8%~6%,因此要重视较大初始风偏角下斜风效应产生的不利影响。
