利用第一性原理计算方法对NbMoTaWVx高熵合金的研究
2018-11-14丁欣恺孙琨张猛方亮邢建东
丁欣恺,孙琨,张猛,方亮,邢建东
(西安交通大学金属材料强度国家重点实验室,710049,西安)
高超声速火箭撬实验平台作为20世纪末发展起来的一种实验设备,对国防建设起着十分重要的作用[1-2]。高速运行火箭撬的关键部位材料需承受高温高压等极端条件,为保证零部件的可靠性与安全性,选用的材料须具有优良的高温耐磨耐腐蚀性能与热强韧性能。实验证明,高熵合金尤其是难熔高熵合金,在高温高压等极端条件下依旧能保持简单的密排晶体结构和优良的综合力学性能[3]。
高熵合金这一概念于2004年首先由我国台湾学者Yeh等人提出[4-7],并引起了广泛的关注。目前比较公认的观点是,高熵合金是由多种金属组元以近等物质的量比混合而成的一种具有高混合熵或者构型熵的合金。这是一种新的合金设计理念,并有望突破传统材料的性能极限[8]。研究表明,多数高熵合金是由1种或2种简单的相构成的。高熵合金的单相结构之所以能稳定存在,根据热力学定律G=H-TS(式中:G为吉布斯自由能;H为焓;T为开氏温度;S为熵),是由高熵合金的高混成熵和低生成焓所决定的。高熵合金具有的高熵效应、晶格畸变、迟滞扩散效应和“鸡尾酒”效应使其具有良好的综合力学特性,如高强度、高硬度、耐磨耐腐蚀性,同时具备良好的塑性等[9]。因此,高熵合金具有巨大的研究价值和广泛的应用前景[10]。
2010年,美国的Senkov教授等人采用真空熔炼法制出了NbMoTaW和NbMoTaWV难熔高熵合金[11-12],此外,他们还设计出了TaNbHfZrTi高熵合金[13],开启了难熔高熵合金的研究热潮。通过将难熔金属元素(如W、Nb、Hf、Zr、Ta、Mo、Yb等)添加进合金组,可分熔炼成难熔高熵合金。以NbMoTaW和NbMoTaWV难熔高熵合金为例,这2种合金相的结构均为单一体心立方结构,在保持多主元合金的单一体心立方相稳定的同时,获得了比普通高熵合金高得多的强度,特别是在高温环境下,力学特性表现尤为突出。
目前国内外对于高熵合金的研究主要为通过实验探索其性质[9],高熵合金的理论研究依旧进展缓慢。另外,实验中高熵合金的组元含量不易控制,高熵合金制备方法的复杂性限制了高熵合金领域研究的快速发展,而基于密度泛函理论的第一性原理计算方法可以方便地从理论计算角度系统地研究高熵合金,目前已有相关研究成果[14-16]。这对于从微观电子结构角度加深对高熵合金的认识十分必要。本文通过第一性原理计算方法对NbMoTaWVx(x表示V组元与其他组元的物质的量比,后文简称量比,0≤x≤1.5;其余各组元的物质的量为1)高熵合金进行了研究,分析了其相与结构性质和弹性力学性质。
1 计算方法
目前,基于密度泛函理论框架下的精确糕模势轨道(exact muffin-tin orbitals,EMTO)结合相干势近似模型(coherent potential approximation,CPA)的方法已经被用于研究高熵合金的结构及其他性质,因此本文所采用的第一性原理计算方法即是此方法[17-18]。EMTO方法通过采用优化的交叠势球构型和全电荷密度来分别描述单电子势函数和计算体系的总能量。当用它来求解Kohn-Sham方程时,不仅可以提高计算效率,同时也能保证体系总能量具有足够的计算精度。CPA方法可以解决第一性原理计算过程中的多主元置换型固溶体的无序性模型问题。由此可见,EMTO-CPA方法是有效解决多主元复杂合金第一性原理计算问题的方法之一。

对9~11个不同的能量-体积点用Morse函数进行拟合,该函数的参数即为计算过程中的总能量、平衡晶格体积和体积模量。立方晶系中2阶弹性常数c11和c12通过体积模量B=(c11+2c12)/3和四方剪切模量c′=(c11-c12)/2解出,c44则通过体积不变的单斜变形所得出的能量与变形率的二次函数关系获得。c11、c12、c44互相独立。合金的多晶模量,如剪切模量G、杨氏模量E、泊松比ν等则通过Voigt-Reuss-Hill定律[20]计算获得。
2 结果与讨论
2.1 相与结构性质
通过对NbMoTaWVx高熵合金的第一性原理计算,证实了在bcc、fcc、hcp结构中,NbMoTaWVx高熵合金的bcc结构在热力学上是最稳定的,这与相关文献[11-12]的实验结果一致。
NbMoTaWVx高熵合金的平衡态WS半径、相对能量和密度见表1,可以看出:随着V组元量比的增加,NbMoTaWVx高熵合金的平衡态WS半径和密度均下降;当V组元的量比由0增大到1.5时,合金的WS半径由15.95 nm降至15.67 nm,降低了1.755%,而密度则由13.53 g·cm-3降至11.80 g·cm-3,降低了12.79%。

表1 NbMoTaWVx高熵合金的平衡态WS半径、相对能量和密度
注:①为fcc结构相对于bcc结构的总能量差;②为hcp结构相对于bcc结构的总能量差;③为NbMoTaWVx高熵合金的密度。
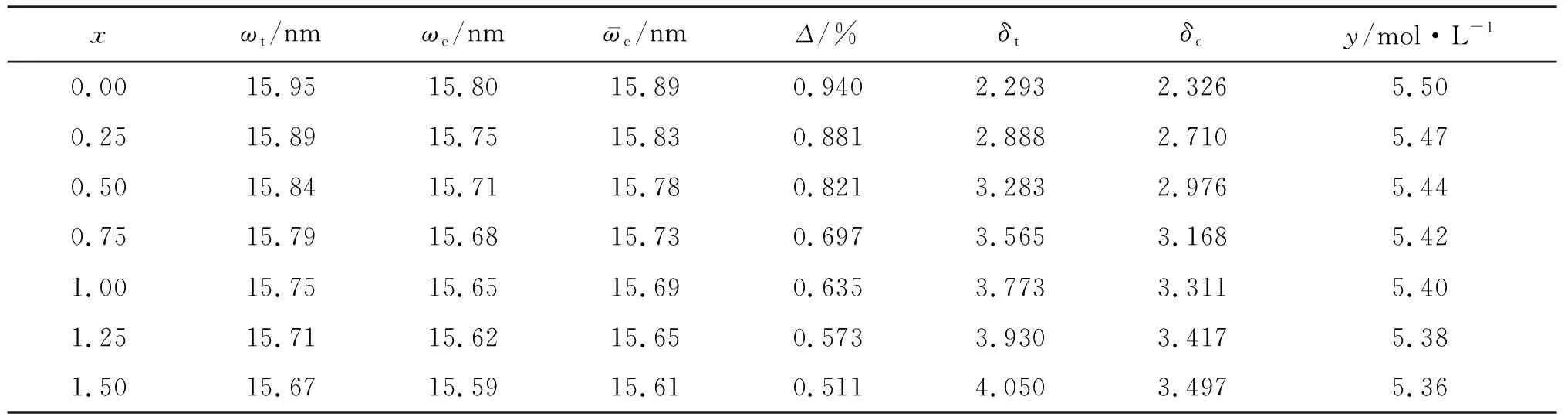
表2列出了高熵合金各组元的结构类型、平衡态WS半径以及体积模量的理论计算值和实验值[11,17],其中,ωt和ωe分别为采用EMTO方法得出的平衡态WS半径理论值和实验值;Bt和Be分别为采用EMTO方法得出的体积模量的理论值和实验值。由表2可知:①由于第一性质原理计算中不包括由于温度因素引起的晶格振动而产生声子的情况,因此本文研究与低温环境下高熵合金的表示类似,在一定程度上可认为高熵合金的纯金属组元在低温下均为bcc结构;②计算得出的平衡态WS半径和体积模量理论值与实验值吻合,这表明考虑温度因素的影响和密度泛函理论方法本身的误差,采用EMTO方法对这些过渡族金属组元的计算误差均在可接受的范围之内;③V组元的平衡态WS半径最小,由此推测V组元的存在缩小了此系列高熵合金的平均晶格尺寸,降低了材料的密度。

表2 高熵合金各组元的结构类型平衡态、WS半径和体积模量

δt和δe分别代表根据理论计算值和实验值得出的原子尺寸差,计算公式为
(1)

平均价电子浓度y的计算公式为
(2)
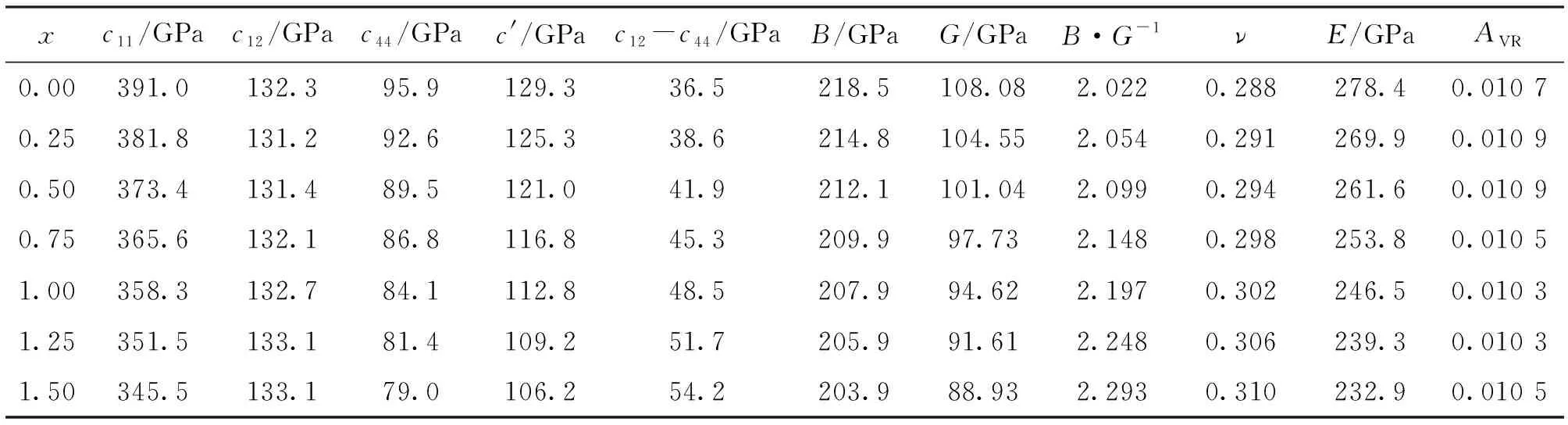
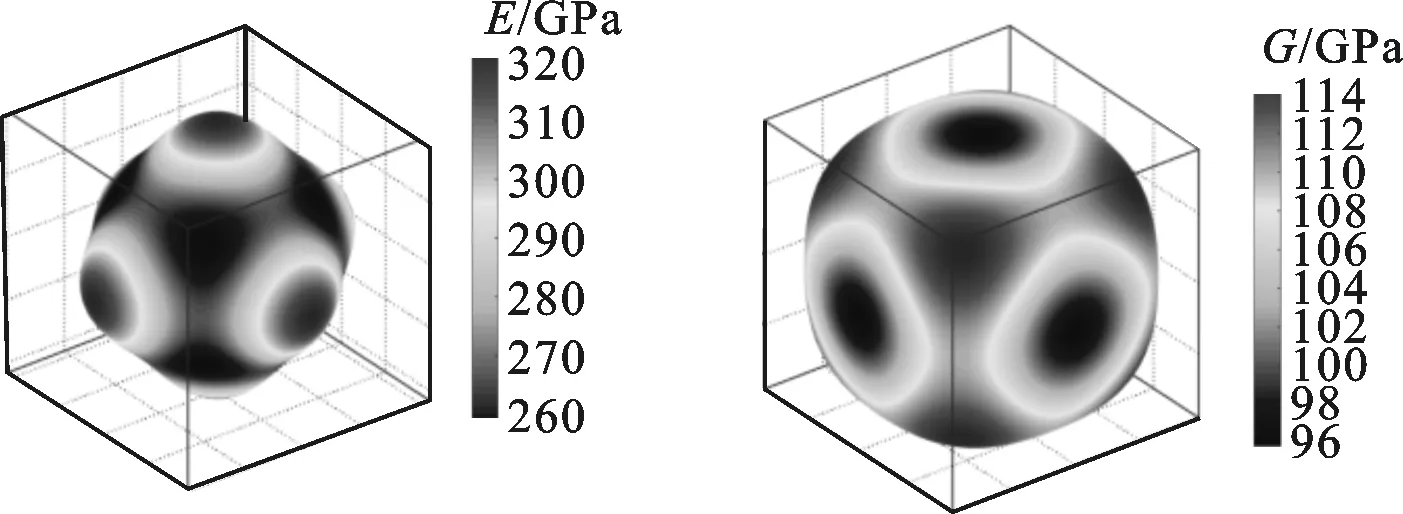
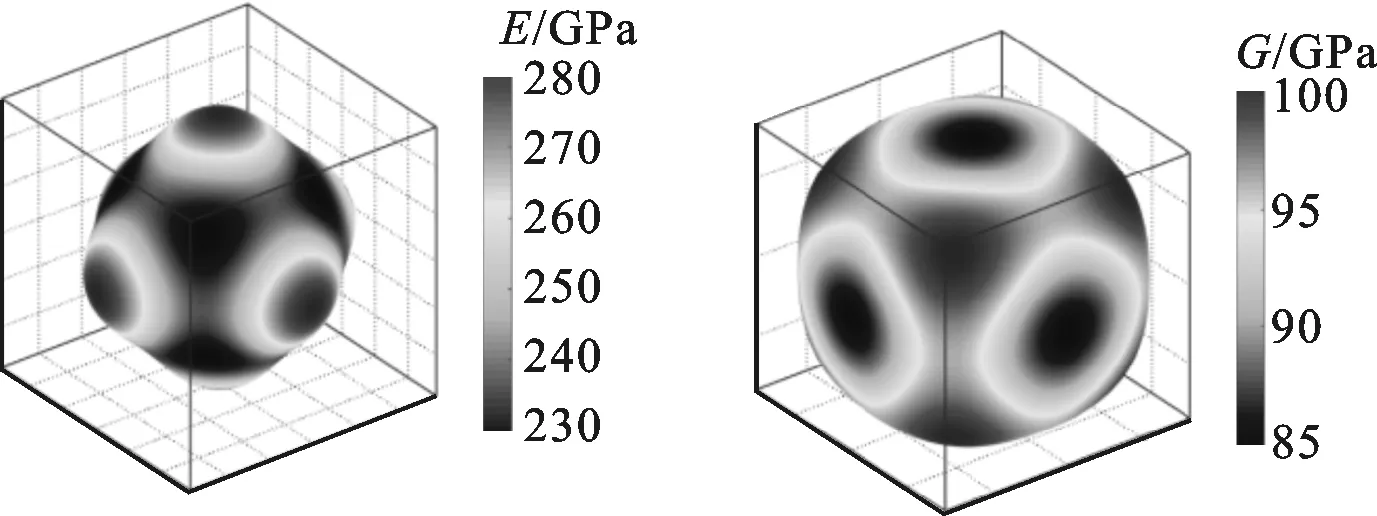
式中ci和vi分别表示i组元金属的量比和价电子浓度。y也经常被用来评估高熵合金相的形成,当4.33 表4中列出了NbMoTaWVx高熵合金的弹性常数、四方剪切模量c′、柯西压力c12-c44、体积模量B、剪切模量G、Pugh比B/G、泊松比ν、杨氏模量E和弹性各向异性系数AVR。本节对NbMoTaWVx高熵合金的弹性常数c11、c12、c44,四方剪切模量c′以及柯西压力c12-c44展开分析。由于目前缺乏相关合金的弹性常数实验数据,故本文无对照数据。 根据立方晶系的热力学稳定性判据[23] c44>0;c11>|c12|;c11+2c12>0 (3) 结合表4中的数据,可知NbMoTaWVx高熵合金在热力学上是稳定存在的。 c′随着V组元量比的增加而降低,表明V组元量比的增加会降低合金体系的bcc结构的稳定性,与表1的结论一致。 在过渡族金属中,c′与不同晶体结构的能量差有关[24]。这一观点在由过渡族金属组元形成的高熵合金中同样适用。文献[25]指出:材料的柯西压力c12-c44与结构内部的成键特性有关;柯西压力c12-c44为正表明材料金属键特性强,柯西压力c12-c44为负则表明材料共价键特性强。显然,V组元量比的增加使得柯西压力c12-c44一直为正且不断增大,表明V组元可使合金的金属性增强。另外,对于由过渡族金属组元形成的高熵合金,合金的平均价电子浓度会对其结构产生一定的影响[21]。V组元量比的增加会导致合金体系平均价电子浓度下降,更倾向于形成密排结构,与文献[26-27]的实验结果相符。 表3 NbMoTaWVx高熵合金的平衡态WS半径、相对误差、原子尺寸差和平均价电子浓度 表4 NbMoTaWVx高熵合金的弹性常数、四方剪切模量c′、柯西压力c12-c44、体积模量B、剪切模量G、Pugh比B/G、泊松比ν、杨氏模量E和弹性各向异性系数AVR NbMoTaWVx高熵合金的各项多晶弹性模量,如体积模量B、剪切模量G、Pugh比B/G、泊松比ν杨氏模量E均已在表4中列出,可以看出:当V组元的量比由0增加到1.5时,体积模量B由218.5 GPa降至203.9 GPa;剪切模量G由108.08 GPa降至88.9 3 GPa;Pugh比B/G由2.022增至2.293;泊松比ν由0.288增至0.310;杨氏模量E由278.4 GPa降至232.9 GPa。值得注意的是,Pugh比B/G和泊松比ν与柯西压力c12-c44的变化趋势一致。这表明在高熵合金中加入V元素后,合金的金属性增强,材料的内在塑性有所提高,理论强度有所下降。材料的塑性和强度均为宏观测量值,由多种因素共同决定,如位错塞积、晶粒细化和固溶时效等。本文仅讨论采用第一性原理计算方法得到的材料电子结构对材料宏观量的影响。文献[11]指出,当NbMoTaW高熵合金中加入V元素后,会产生晶粒细化和类固溶强化现象。这个因素对材料强度和塑性宏观量具有很大的影响,但材料的电子结构等内在因素也不容忽视。 材料的韧脆性可由Pugh比B/G和泊松比ν来进行评价。当B/G>1.75时,材料被视为韧性材料;当B/G<1.75时,材料被视为脆性材料[28]。NbMoTaWVx高熵合金的Pugh比B/G在0≤x≤1.5时为0.31,表现为韧性材料。另外,文献[29]指出,对于某些非晶合金,当泊松比ν>0.31时,材料表现为韧性,当泊松比ν<0.31时,材料表现为脆性。NbMoTaWVx高熵合金的泊松比ν在0≤x≤1.5时表现为脆性。可以看出,根据不同标准判断得出的高熵合金的韧脆性是不同的。要注意的是,无论使用哪种标准,结果均表明V组元量比的增加可以改善材料的内在韧性。因此,不能完全依靠Pugh比B/G或泊松比ν来评价和预测高熵合金的韧脆性。 NbMoTaWVx高熵合金的弹性各向异性系数AVR已在表4中列出,其计算公式为 AVR=(GV-GR)/(GV+GR) (4) 式中:GV表示按Voigt方法计算出的剪切模量;GR表示按Reuss方法计算出的剪切模量;GV与GR具体由弹性常数c11、c12和c44根据相关公式计算得出[23]。当AVR为0时,材料表现为各向同性。从表4可以看出,NbMoTaWVx高熵合金的弹性各向异性系数AVR在0≤x≤1.5时保持在0.01左右,表明V组元量比的增加对NbMoTaWVx高熵合金弹性的各向异性几乎不产生影响。文献[30]的研究指出,高熵合金的弹性各向异性与平均价电子浓度存在联系。对比表3的数据可以发现,V组元量比的增加会略微降低合金的平均价电子浓度,这与弹性各向异性系数的变化趋势相符,但NbMoTaWVx高熵合金与平均价电子浓度的关系有待理论与实验上的进一步探究。 为反映V组元对NbMoTaWVx高熵合金弹性各向异性的影响,图1给出了NbMoTaW和NbMoTaWV两种高熵合金的杨氏模量E和剪切模量G的特征曲面分布图。从图1a可以看出,NbMoTaW高熵合金的杨氏模量E的最大值为320 GPa,位于<001>晶向,最小值为260 GPa,位于<111>晶向;从图1b可以看出,NbMoTaW高熵合金的剪切模量G的最大值为114 GPa,位于<111>晶向,最小值为96 GPa,位于<001>晶向,与杨氏模量空间的分布情况相反;从图1c可以看出,NbMoTaWV高熵合金的杨氏模量E的分布情况与NbMoTaW高熵合金相同,杨氏模量E从230 GPa增加到280 GPa,最大值位于<111>晶向,最小值位于<001>晶向;从图1d可以看出,NbMoTaWV高熵合金的剪切模量G从85 GPa增加到100 GPa,最大值位于<001>晶向,最小值位于<111>晶向。 (a) NbMoTaW的杨氏 (b) NbMoTaW的剪切模量E 模量G (c) NbMoTaWV的杨氏 (d) NbMoTaWV的剪切模量E 模量G图1 NbMoTaW和NbMoTaWV高熵合金的杨氏模量E和剪切模量G的特征曲面分布图 本文采用第一性原理计算方法研究了NbMoTaWVx高熵合金,分析了其在平衡态条件下的相结构和弹性力学性质,结果表明:NbMoTaWVx高熵合金在热力学上最稳定的相为bcc结构;V组元量比的增加会导致此系列高熵合金的密度下降和晶格变小,并降低bcc相的稳定;NbMoTaWVx高熵合金的柯西压力c12-c44、Pugh比B/G和泊松比ν随着V组元量比的增加而增加,材料的内在塑性随之提高,理论强度有所下降;Pugh比B/G和泊松比ν均不能完全评价和预测合金的韧脆性;V组元量比的增加对NbMoTaWVx高熵合金的弹性各向异性几乎不产生影响。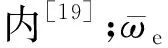
2.2 弹性常数
2.3 多晶弹性模量
2.4 弹性各向异性
3 结 论
