基于灰色理论预测人口新政策对经济发展的影响

朱家明，胡榴榴，王 杨，胡逸群

(安徽财经大学 a.统计与应用数学学院;b.国际经济贸易学院，安徽 蚌埠 233030)

1971年，“有计划地增长人口”被确定为我国既定的人口政策。这项特殊的人口政策在一定程度上控制了我国人口增长的速度，但也带来了另一重大人口问题：过高的人口老龄化。我国政府改变人口政策，逐步放开生育政策，推行“全面二孩”政策。这一政策在社会各界引起了激烈讨论。林杰等对基于不同政策对人口结构的影响进行了研究[1]，李咏馨等基于综合评价法对人口可持续发展模型进行了研究[2]，本文基于Leslie矩阵和灰色预测模型，研究“全面二孩”政策对我国人口结构的影响。

一、基于Leslie模型分析新政策对我国未来人口的预测

(一)数据准备

利用“全面二孩”政策实施之前中国国家统计局公布的全国人口普查数据，根据最近五年(2012—2016)数据得出不同年龄阶段的妇女生育人数，并计算出不同年龄阶段妇女生育人数占总出生人数的比重(简称出生比)，见表1。

表1 不同年龄阶段妇女生育人数占总出生人数的比重

(二)研究方法

我们利用Matlab软件建立Leslie矩阵[3]，对我国2017—2030年人口情况进行预测分析。

将人口按年龄大小等间隔地划分为若干个年龄组，假设人口的生育率与死亡率不随时段k变化，只与年龄组有关。记存活率为Si(1-死亡率)，生育率为bj。

人口数量为xi(k)的变化规律为：当时段k+1时，第一个年龄组的数量是各年龄组在时段k的生育数量之和；第i+1年龄组(i=1,2，…，m-1)的数量是时段k第i年龄组存活下来的数量。由此得到

(1)

xi+1(k+1)=sixi(k),k=0,1,2,…;i=1,2,…，m-1

(2)

其中(1)(2)是差分方程，记人口数量在时段k按年龄组的分布向量

x(k)=[x1(k),x2(k),…,xm(k)]T,k=0,1,2,…

则(1)(2)可表示为x(k+1)=Lx(k),k=0,1,2,…

当矩阵和年龄按年龄组的初始分布x(0)已知时，可以预测人口数量在时段k按年龄组的分布为x(k)=Lkx(0)，k=1,2，…

通过使用Matlab软件，依据往年的总人口、女性人口、出生婴儿数等数据，计算出该年份的生育率、繁殖率、女性人口比率、存活率，建立Leslie矩阵L，通过公式计算出，如表2所示。

表2 2017—2030年我国总人口数(单位：亿人)

同时利用该模型计算出(0—14岁、14—64岁、65岁及以上)的人口数量，见表3。

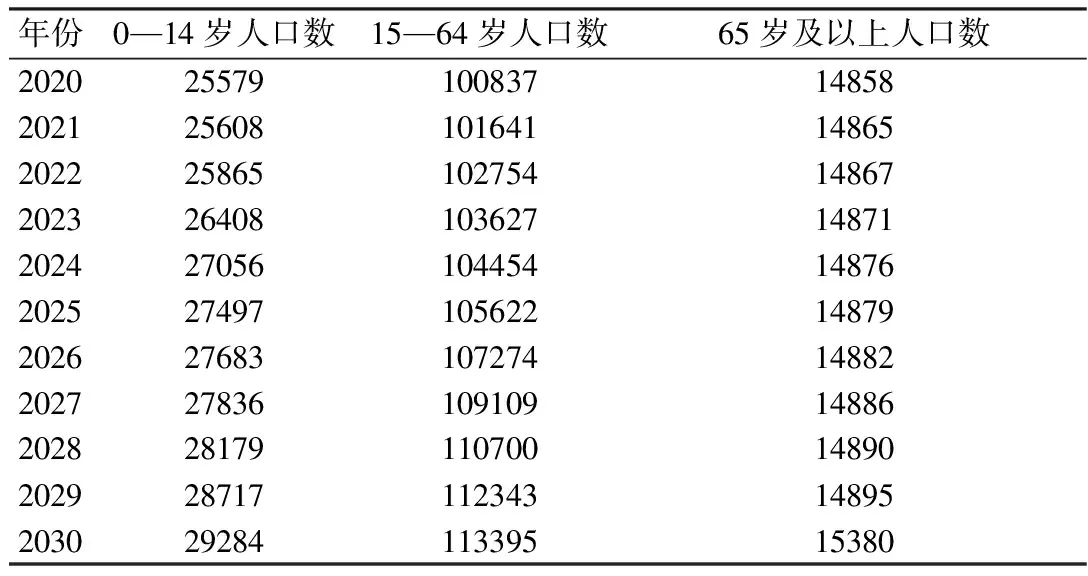
表3 “全面二孩”政策下2020—2030年中不同年龄结构 (单位：万人)

(三)结果分析

将Leslie矩阵的结果(“全面二孩”政策下2017—2030年我国人口总人数)绘制成折线图，如图1所示。

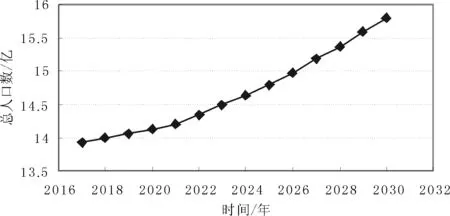
图1 2017—2030年我国总人口数

从Leslie矩阵计算得出的结果可以看出，实施“全面二孩”政策之后，我国的人口总数显著上升，且上升速度不断变快，说明“全面二孩”政策实施下我国人口出生率有了显著提升。由此可以得出，这一政策的实施对于我国人口红利逐渐消失的现状有积极影响。

二、基于多元回归分析人口结构变化对经济发展的影响

(一)数据准备

查找并整理得出过去20年我国人均GDP、0—14岁人口数、15—64岁人口数、65岁及以上人口数、总抚养比、少儿抚养比、老年抚养比、人口出生率、人口死亡率和人口自然增长率。

(二)研究方法

1.相关分析

以人均GDP为被解释变量，分别以0—14岁人口数、15—64岁人口数、65岁及以上人口数、总抚养比、少儿抚养比、老年抚养比、人口出生率、人口死亡率和人口自然增长率为解释变量，做相关分析，并得出线性值[3-4]，见表4。

由R2线性值可以看出，0—14岁人口数、15—64岁人口数、65岁及以上人口数、少儿抚养比、老年抚养比、人口死亡率与人均GDP成较强的线性关系，总抚养比、人口出生率和人口自然增长率与人均GDP线性关系较弱，故而剔除总抚养比、人口出生率和人口自然增长率3个因素。

2.回归分析

建立0—14岁人口数(X1)、15—64岁人口数(X2)、65岁及以上人口数(X3)、少儿抚养比(X4)、老年抚养比(X5)、人口死亡率(X6)与人均GDP(Y)的回归方程[2，5]，得出回归方程如下：

Y=-94971.93-5.830X1+0.3965X2+26.7606X3+5910.311X4-19989.81X5+1016.823X6

表4 各变量的R2线性值

由回归分析结果得出，F检验对应的概率值为0.00，小于0.05，各因素对方程的影响较为显著。但由t检验可以看出15—64岁人口数(X2)、人口死亡率(X6)的t检验不通过，因而剔除这两个因素再做回归分析。得出新的回归方程如下：

Y=-4673.53-5.72X1+30.59X3+5729.21X4-23882.49X5

做自相关检验发现0—14岁人口数(X1)与少儿抚养比(X4)相关性较强，65岁及以上人口数(X3)与老年抚养比(X5)相关性较强，因而对回归模型进行调整，最终以0—14岁人口数(X1)、65岁及以上人口数(X3)为解释变量，以人均GDP为被解释变量，进行多元回归分析。得出回归方程如下：

Y=-89357.46+0.664598X1+8.781313X3

最终，把Leslie矩阵计算出的2020—2030年我国人口情况代入回归方程，得出“全面二孩”政策实施下我国人均GDP情况，见表5。

表5 实施“全面二孩”政策下的人均GDP(单位：元)

(三)结果分析

从相关分析可以看出，人口结构的变化会对我国人均GDP产生影响，尤其是老年人口数量和老年抚养比对于人均GDP的影响尤为显著；从多元回归分析可以看出，近些年我国人均GDP一直呈上升趋势。当然，影响人均GDP除人口结构以外还有其他多种因素,回归分析的结果只能在一定程度上反映人口增长与经济发展呈同方向变动，且这一发展状况是基于我国特定国情的。

三、我国人口合理化发展的生育政策建议

(一)研究思路

首先预测出不实施“全面二孩”政策下我国的人口结构情况，并将人口结构情况代入多元回归方程得出不实施人口政策下我国的经济情况预测；然后将它与“全面二孩”政策实施下的经济情况预测进行对比，进而给出合理化的生育政策建议。

(二)研究方法

根据收集到的1996—2015年我国人口结构情况，利用Matlab建立灰色预测模型[5-6]，预测出实施“全面二孩”政策下2020—2030年我国人口结构的情况，见表6。

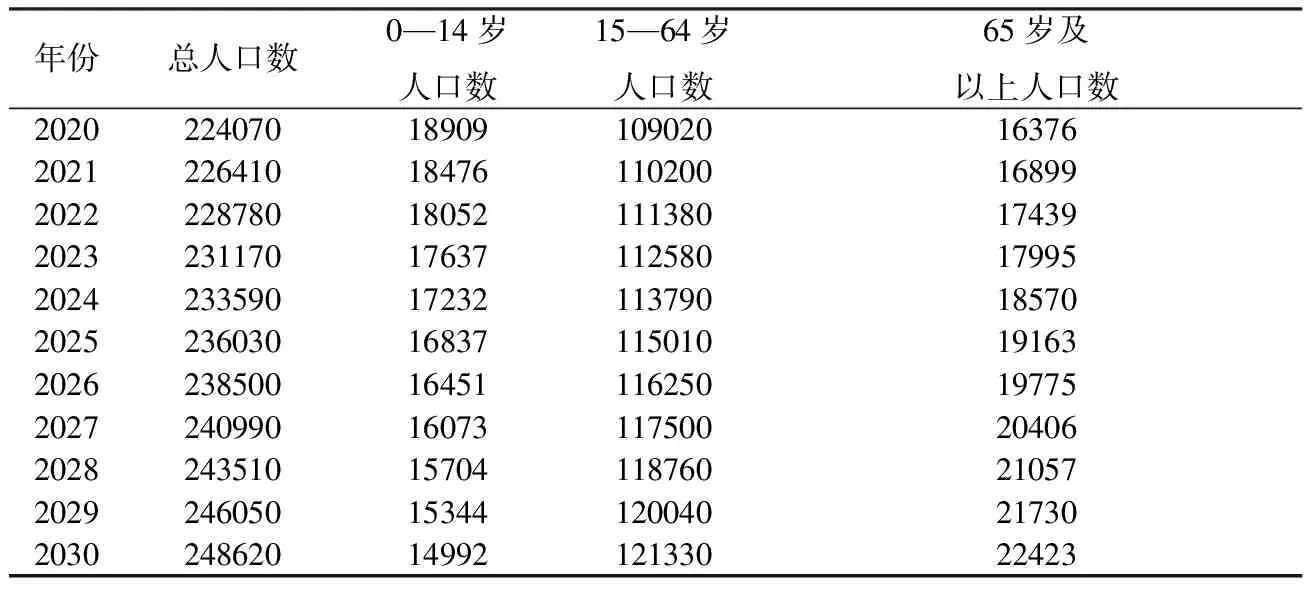
表6 “全面二孩”政策下2020—2030年我国人口结构(单位：万人)

以0—14岁人口数、65岁及以上人口数为自变量，代入上述回归方程对人均GDP进行预测，得出不实施“全面二孩”政策下2020—2030年我国人均GDP预测情况，见表7。

表7 不实施“全面二孩”政策下2020—2030年我国人均GDP(单位：元)

(三)结果分析

由回归分析得出实施“全面二孩”政策与不实施“全面二孩”政策下我国人均GDP情况如图2所示。

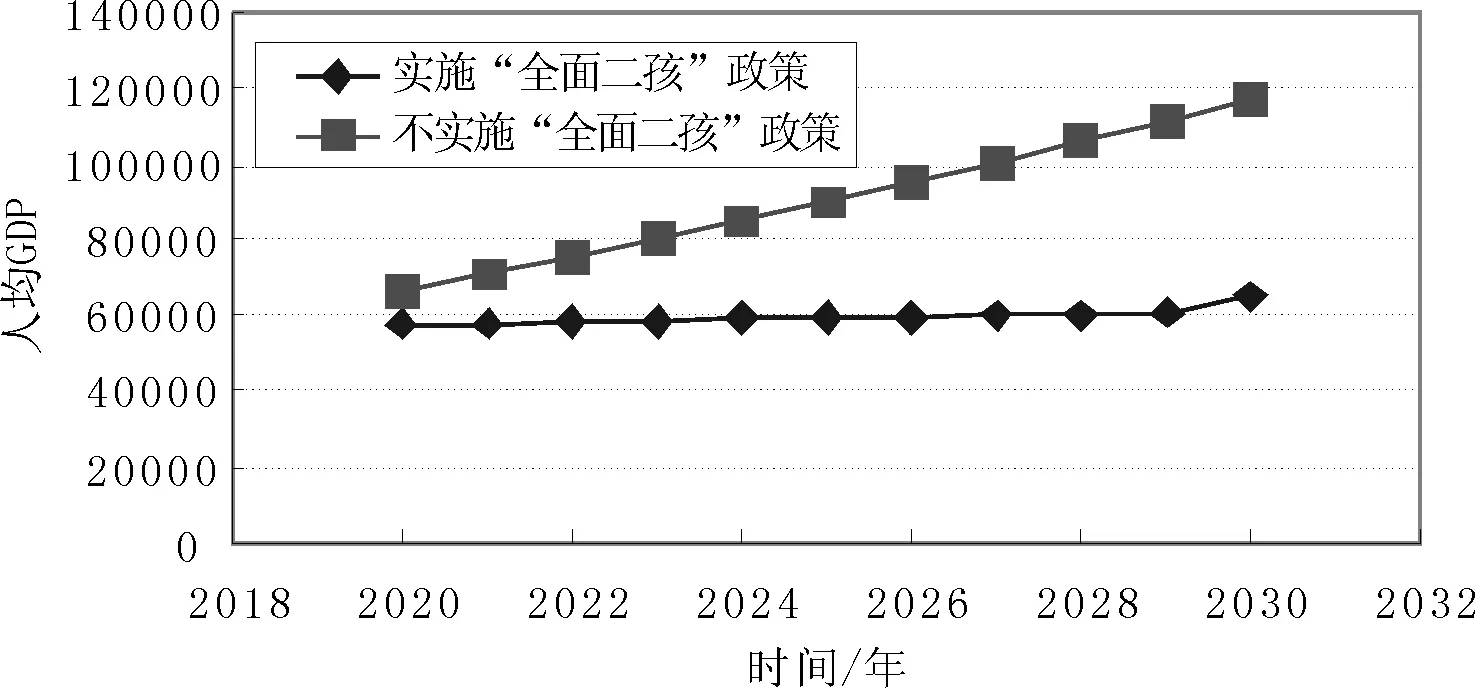
图2 实施“全面二孩”政策与不实施“全面二孩”政策下我国人均GDP

根据回归分析可以看出，无论是否实施“全面二孩”政策，我国人均GDP发展态势都呈上升趋势，但实施“全面二孩”政策下的人均GDP增长幅度明显要低于不实施“全面二孩”政策下的人均GDP增长幅度。由此可以看出，从短期来看，“全面二孩”政策的实行可能会使得我国的经济增长速度放缓，这可能是“全面二孩”政策实行后不断增加的生育费用、婴幼儿抚养费用等导致的。但从长期来看，“全面二孩”政策可以改变我国人口老龄化程度，改善我国的人口结构，提高我国劳动力数量，这是有利于我国经济长期发展的。

综上所述，关于我国的生育政策，给出以下建议[6]。

第一，要实施适当的“全面二孩”政策，辅之以一定程度的生育限制。过高的生育率除了降低人口老龄化，还会带来高的社会抚养比，在短期内会减缓经济发展的幅度。

第二，人口政策的实施需要结合民情。如果普遍社会生育率不高，人们生育积极性低，可以进行一定的鼓励生育政策，人口老龄化是我国当前人口发展的重大问题，长期发展下去必然带来社会抚养比提高，劳动力缺失等不利于经济发展的现实问题。

第三，把握好实施生育政策的度，及时根据社会实际情况对生育政策进行调整；综合考虑生育政策可能带来的各方面影响，选取最为合理的生育政策。

第四，人口出生率不仅仅受到人口政策的影响，还会随着社会环境、人们心理因素的变化不断发生变化。因此，生育政策的选择，还需考虑到心理因素的影响。

四、结束语

综合利用Leslie矩阵、灰色预测模型对实施“全面二孩”政策和不实施“全面二孩”政策下我国人口数量和结构进行预测，同时利用回归分析得出人口结构变动对我国经济发展的影响，并将预测得出的人口结构代入回归方程预测出我国未来的人均GDP。预测结果显示，在不考虑其他因素的影响下，“全面二孩”政策的实施，在短期内会减缓我国经济增长态势；但从长期来看，这一政策的实施是有助于改善我国目前不合理的人口结构的。任何一个政策的实施都是具有两面性的，在给我们带来利益的同时也会有一定缺陷，我们要在协调发展的基础上辨证地选择政策，对于人口问题更应在可持续发展的基础上用全面的眼光衡量。