范数正则化约束雷达角度维高分辨方法研究*

张 良,吴海兵,周 杰,陶海军

(陆军军官学院,合肥 230031)

0 引言

雷达分辨率包括距离和横向分辨率,其中距离分辨率由信号带宽决定;横向分辨率即角度分辨率,则由天线波束宽度所决定。雷达分辨率直接影响了目标探测的最终精度和准确度,是雷达性能参数的最重要的指标之一[1]。

实现雷达距离维的高分辨率,可以采用大带宽信号的发射方式,然后利用脉冲压缩及相关的超分辨率技术获得;实现角度维的高分辨率,传统方法通常采用多普勒波束锐化(doppler beam sharpening,DBS)和合成孔径雷达(synthetic aperture radar,SAR)技术[2],即利用雷达与目标之间的相对运动产生的变多普勒频率来获得。但是DBS和SAR存在前视盲区[3],这是因为雷达回波的多普勒频率变化率在前视模式下几乎为零,直接造成角度分辨效果的急剧下降。因此实际雷达系统为了兼顾前视分辨能力,常采取实波束角度分辨技术,这时雷达天线孔径大小决定了角度分辨能力[4]。但是由于实际系统研制成本的限制,很难将天线孔径做成满足方位精度需求的尺寸。

经典的实波束雷达测角技术,包括基于解卷积技术的测角方法[5]和单脉冲雷达和差波束测角方法[6]。其中解卷积技术利用对发射的雷达信号和接收的回波数据进行解卷积处理回溯待求解的目标角度信息。由于单通道雷达的天线方向图存在空间频域的“零点问题”,通常导致解卷积技术不适定(也称病态的),造成求解结果不稳定;单脉冲雷达测角技术的核心思想是通过提取回波和差通道接收信号的差异信息,进行目标角度的有效测量,通常具有较高的测角精度。但当波束中同时出现多个目标时,测角性能会急剧下降,此时只对特殊构型的目标角度分辨效果比较好,因此也存在一定局限性。

根据信号建模过程可知,实波束雷达的接收回波是由天线方向图和目标角度信息进行卷积的结果。因此在对时域积分回波方程进行矩阵和矢量化的离散处理之后,可以采用经典的最小二乘(least square,LS)方法进行求解目标方位信息。然而,上述方法在噪声情形下通常是不适定性的[7],导致求解结果存在严重偏差。据此,文中考虑采用范数正则化技术来解决上述问题。首先基于最小二乘求解方式分析噪声条件下求解该线性方程组存在不适定性问题,接着提出了基于TSVD[8]及Tikhonov[9]正则化方法的测角技术,即通过修正求解模型的方式减弱解的不适定性问题,实现对真实解的近似或逼近。

最后,利用雷达待探测目标的在空域上往往是稀疏的(尤其是对空目标,它们的数目通常是有限的)先验信息,进一步约束求解目标的信号模型,将雷达角度维的信号参数估计问题转化为稀疏信号表示问题,并提出基于正交匹配追踪(orthogonal matching pursuit,OMP)算法[10]的高精度测角技术。仿真结果表明,相比经典雷达测角方法,所提方法均具有较高的角度求解精度,并在较低信噪比条件下能够实现角度维的重构效果。

1 信号模型

实孔径雷达的角度分辨率主要由天线波束宽度决定,通常以波束的3 dB宽度作为衡量标准,因此可以采用发射极窄雷达波束的方法来改善目标的角度维分辨效果,但是这需要研制非常大口径的天线,一方面研制成本非常高,另外一方面考虑实际可实现性,这种方式的的波束锐化往往是有限的。因此实际中可以采用解卷积方法,通过在软件方面可以改善目标的分辨率。实孔径雷达测角的基本原理如图1所示。

从图1可以看出,当两个目标相距较近时,目标散射信息和天线方向图卷积的结果会在时域上叠加,接收的目标回波是经过带通天线方向图的调制结果,此时无法将两个目标进行区分。但是利用解卷积处理等信号处理手段,可以使得多个目标的回波信号波峰分裂,实现方位维上的多个目标分辨能力。

设目标方位信息为x(t),雷达天线方向图函数为h(t),雷达接收回波信号为y(t),接收机的高斯白噪声为n(t),雷达以T为周期对回波进行采样,则在时间域上满足如下关系

(1)

依据空时等效性,在空域上有(雷达角度扫描间隔为Δθ=vT)

(2)

式中：n=1,2,3,…,N；N为采样点数。容易看出式(1)与式(2)是一致的。设采样间隔为Δθ,通过对回波信号进行采样,雷达接收回波信号建模为

y(nΔθ)=x(nΔθ)·h(nΔθ)+n(nΔθ)

(3)

因此,雷达前视回波数据y(θ)是目标角度信息x(θ)与天线方向图h(θ)的卷积结果,即

y(θ)=x(θ)·h(θ)+n(θ)

(4)

对式(4)进行傅里叶变换,可以得出

Y(ω)=X(ω)·H(ω)+N(ω)

(5)

根据逆滤波原理求得目标方位向信息为

IFFT{[Y(ω)-N(ω)]/H(ω)}

(6)

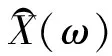
接着,可用常见解卷积方法,如CID[11],FCID[12],FCID-CID[13]算法求解式(6),进而得出角度维目标信息,但这些方法的测角效果在信噪比较低情形下通常并不理想。

2 基于范数正则化约束的测角技术研究

本节将求解方位角度信息转化成线性方程的求解。首先基于最小二乘求解方式分析了噪声条件下求解该线性方程组存在不适定性问题。接着提出了基于TSVD及Tikhonov正则化方法的测角技术,可以较好地修正不适定性问题的同时,获得对原始解的逼近值。最后基于实际场景中目标个数有限的情形(即利用目标稀疏先验信息),引入稀疏重构技术。提出基于OMP算法的测角方法,既能克服其病态性问题,又具有较快的重构速度及较小的重构误差。

2.1 不适定问题分析

将式(4)转换成矩阵形式,即

y=Hx+n

(7)

为讨论方便,这里假设回波测量值y∈CN×1,系统观测矩阵H∈CN×M,待重构目标矢量x∈CM×1,噪声矢量n∈CN×1。

已知y和H,对x进行求解,可以得出式(7)对应的最小二乘解为

x=(HTH)-1HTy

(8)

对H进行奇异值分解如下式所示

(9)

(10)

下面首先介绍不适定问题的定义[7],若观测矩阵H的奇异值满足

1)奇异值逐步逼近于零。

2)最大奇异值跟最小奇异值的比值非常大。

则称为不适定性(ill-posed)问题(或病态性问题),其中最大奇异值与最小奇异值的比值定义为条件数。因此H的条件数越大,则病态性越严重,由噪声引起的解的扰动也越大。

正则化约束是一种可以较好地解决不适定性问题,并获得稳定真实解的近似值的重构方法。下面介绍本文采用的两种正则化技术——TSVD和Tikhonov。

2.2 基于正则化技术的角度信息提取方法

1)TSVD正则化方法

2)Tikhonov正则化方法

正则化方法的一般形式如下所示

Tikhonov正则化方法就是引入的稳定泛函为P(x)=‖x‖2(后续简称为L2范数方法),此时式(7)应转换为下式

(11)

接着,对式(11)进行广义奇异值分解,可以得到

(12)

由前面分析可知,选择合适的正则化参数对最终求解结果是非常重要的。正则化参数的选取方法目前主要包括3种[20]:离散偏差准则法,广义交叉验证法和L曲线法。由于篇幅限制,这里就不再展开介绍。

2.3 结合目标稀疏先验约束的角度信息提取方法

针对角度维高分辨问题,在观测量y含有噪声的情况下,当所求的解具有稀疏性时,基于最小二乘原理的L2范数正则化方法中的稳定泛函项只能体现解x的光滑性(也称连续性),不能反映出解x的稀疏性,因此利用L2范数正则化方法恢复结果存在较大的误差。

对该类稀疏目标恢复的情形,文中考虑引入稀疏重构算法,实现方位向稀疏目标的高分辨角度信息提取。具体做法为:利用过完备字典方法将式(7)转化为稀疏信号表示问题,并利用近年来流行的压缩感知技术(compressed sensing,CS)[14],将角度信息提取转化为稀疏信号恢复优化问题,可以得到更高的信号重构精度。总所周知,CS技术采用非自适应测量方式,能够大大减少了实际系统的数据测量值,目前已广泛应用至雷达成像、谱估计、目标检测等多个领域。

文中采用正交匹配追踪(orthogonal matching pursuit,OMP)算法,这是因为OMP本身属于贪婪算法的一种,具有非常快的重构速度,其本质是基于稀疏分解的思想:即在每次迭代中通过匹配找到与残余回波最相似的元素,并通过最小二乘方法去除之前所找到的所有元素的影响,再对正交残余回波进行迭代匹配,直至算法收敛。该算法的具体流程参见文献[10]。

3 仿真结果与分析

仿真实验采用辛格(Sinc)型天线方向图,3 dB波束宽度为1.2°,两个目标角度相差0.606°(详细见图2～图4中的红点),天线扫描范围:-10°～10°,扫描速度为40°/s,脉冲重复频率RPF为2 000 Hz。

图2是最小二乘法在信噪比(signal to noise ratio,SNR)为60 dB和30 dB时结果的对比图。可以看出其在高信噪比的情况下反演效果很好,但是在信噪比降低至30 dB后,噪声对解的影响明显能够看出,这体现出之前陈述解的不适定性问题,因此在求解过程中加入一定的约束限制是非常必要的。

图3为在信噪比为20 dB下使用最小二乘法、TSVD(包括仅截断较小的奇异值和同时截断两端过大过小的奇异值两种情形),以及Tikhonov得到的重构结果。

可以看出:在噪声较大时,最小二乘法的反演误差很大;利用TSVD截断过小的奇异值一定程度上可以抑制噪声的影响,利用TSVD同时截断过大和过小的奇异值的方法可以很好的抑制噪声,但是在两目标之间积累噪声,一定程度上会降低角度维分辨率。相比而言,Tikhonov方法展示了较为稳健的重构效果,但恢复的目标散射系数存在一定的偏差。

仿真条件与之前保持一致,图4为OMP方法的测角结果,可以看出加入目标稀疏约束先验之后,基于稀疏重构技术的测角技术具有最好的分辨效果。

下面采用蒙特卡洛方法(共实验50次,然后取平均)获取以上几种方法的性能曲线。图5是反演结果与真实解的均方误差(mean squared error,MSE)随信噪比变化的曲线图,容易得出:1)所有曲线的趋向均是下降,这是由于随着信噪比的提高,反演结果更加接近真实解。2)TSVD的误差曲线与最小二乘法的误差曲线变化相似,但是始终处于其下方,这很好地验证了范数正则化的优势。3)在信噪比为25 dB时,各方法的反演效果优劣排序为OMP算法,L2范数,FCID算法,TSVD,最小二乘法,维纳滤波。

图6则是在信噪比为15 dB情形,OMP和L2范数方法的误差函数随着目标数目(稀疏度)变化的情况,很明显OMP具有更高的测角精度,这与之前的分析也是一致的。

4 结论

文中首先对经典雷达测角技术——基于解卷积技术的测角方法和单脉冲雷达和差波束测角方法的优缺点进行了讨论。接着详细分析了求解原始信号模型时存在不适定性问题,并提出基于TSVD及Tikhonov范数正则化约束的测角技术,使得修正后的信号模型在保证解的真实性同时,较好地克服传统解卷积技术带来的不适定性问题。最后考虑目标场景的稀疏先验约束,提出了基于OMP算法的测角技术。仿真结果验证了所提方法的方法能够提高雷达测角的精度,并且具有较好的抗噪性能。