一种改进的机载武器传递对准中杆臂效应动态补偿方法*

谷 雨,司 帆,赵 剡,张亚崇,3

(1 西安飞行自动控制研究所,西安 710065;2 北京航空航天大学仪器科学与光电工程学院,北京 100191;3 飞行器控制一体化技术国防科技重点实验室,西安 710065)

0 引言

传递对准是机载武器在发射之前的一项重要的初始化工作,其对准精度在很大程度上决定了武器的使用效能[1]。在以往的研究工作中,通常将杆臂矢量看作是固定值,直接在主惯导信息上进行刚性杆臂补偿后作为子惯导的导航参数,当机翼发生结构挠曲变形时,主惯导的精度再高,也会被淹没在由挠曲变形引起的误差中[2],显然该方法没有考虑杆臂效应的产生机理,不能满足高性能的应用需求;此外,很多研究文献将机翼结构动态变形理想化为二阶或三阶马尔科夫过程[3],模型的有关参数全凭经验设定,缺乏实用性[4]。

针对传递对准中杆臂效应动态补偿这一技术难题,文中提出了一种杆臂效应的动态补偿方案:利用挠曲变形估计出杆臂矢量的变化情况,进而对杆臂速度进行补偿,消除由杆臂效应对传递对准的影响。通过“速度+姿态”匹配的仿真结果表明,该方法可有效提高传递对准的精度,并且具有良好的工程实现上的便利性。

1 机翼挠曲变形模型

1.1 挠曲变形

由于实际飞行环境的复杂多样性,机翼的挠曲变形具有时变特征且与机型强相关,是无法准确预测的。由于挠曲变形角可看作是随机作用力影响下的随机变量,为了研究的方便,文中将挠曲变形角建模为白噪声激励下的二阶马尔科夫过程,其模型如下[5]:

(1)

(2)

式中:θ=[θx,θy,θz]T为挠曲变形角;ω=[ωx,ωy,ωz]T为挠曲变形角速率;β=diag(βx,βy,βz)为参数矩阵;ηf=[ηfx,ηfy,ηfz]T为白噪声,其频谱密度Qη为:

Qη=4β3σ2

(3)

1.2 挠曲位移

受挠曲变形角的影响,子惯导会偏离其标称杆臂矢量位置,从而产生挠曲位移。下面以XOZ平面为例,分析挠曲变形角与挠曲位移的关系。图1为机翼挠曲变形示意图。R为子惯导的实际杆臂矢量,Rf为子惯导的挠曲位移向量,OmXmZm为主惯导处的载体系,OsXsZs为子惯导处的载体系,Lx为主、子惯导标称杆臂矢量的X轴分量,θy为绕机体纵轴的挠曲变形角。当θy为小角度时,机翼可看作是一段均匀的圆弧,一般可将B点视作线段OA的中点。

根据图中几何关系可得:

θy=2∠BOmOs

(4)

(5)

∠BOmOs+∠BOsOm+∠BOsA+∠BAOs=180°

(6)

联立式(5)、式(6)可得:

∠BOsOm+∠BOsA=90°

(7)

即∠OmAOs为直角,则挠曲位移向量Rf可表示为:

(8)

取小角度近似条件sinθ≈θ,cosθ≈1,则式(8)可简化为:

(9)

同理,扩展到XOY和YOZ平面,Rf可表示为:

(10)

经过挠曲位移补偿后,实际杆臂矢量可表示为:

R=L+Rf

(11)

以上建立了机翼挠曲变形影响下杆臂矢量的变化模型,通过式(11)可对传递对准中的杆臂效应进行补偿。

2 动态杆臂效应的分析

如前所述,由于杆臂矢量不再是常值,杆臂效应也变得更加复杂。为了能够精确补偿,这里对动态杆臂矢量影响下的杆臂效应进行详细分析。

图2中,Rm和Rs分别为主、子惯导在地球系的位置矢量,R为杆臂矢量。根据图中矢量关系可得:

Rs=Rm+R

(12)

由于惯导输出的速度是相对于地球的,将式(12)相对于地球系求一阶导数,并根据哥氏定理可得:

(13)

式中:e表示地球系;m表示主惯导载体系。将式(13)投影至地理系(t系)可得:

(14)

将式(12)相对惯性系求二阶导数,可得到主、子惯导的比力关系:

(15)

(16)

(17)

式中:fm和fs分别为主、子惯导加速度计的比力;gm和gs分别为主、子惯导处的重力加速度。

将式(15)投影至主惯导载体系,并考虑到gm与gs近似相等[6],可得:

(18)

3 速度+姿态匹配对准模型

本节以“速度+姿态”匹配传递对准为例,详细说明如何在对准模型中对挠曲变形进行处理的方法。

3.1 状态方程

系统状态变量取为:

(19)

则系统状态方程可写为[4,7]:

(20)

式中:系统矩阵F为:

(21)

系统噪声为:

(22)

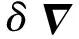
噪声矩阵为:

(23)

3.2 量测方程

由于主惯导的精度远高于子惯导,因此可认为主惯导是无误差的。取姿态匹配量测阵为[8]:

(24)

受挠曲变形角θ与安装误差角ξ的影响,主、子惯导坐标系之间的关系如图3所示。因此,姿态量测矩阵可分解为:

(25)

考虑到φ、ξ、θ都是小角度,则:

(26)

(27)

(28)

将式(26)～式(28)代入式(25),并忽略二阶小量,可得:

(29)

取姿态匹配量测量为:

(30)

则量测方程为:

(31)

速度匹配的量测量为:

(32)

(33)

联立式(14)和式(33),可得:

(34)

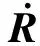
联立式(31)和式(34),可得速度+姿态匹配的量测方程:

Z=HX+v

(35)

式中：Z=[φ,δV]T为量测向量;v为量测噪声;量测矩阵H为:

(36)

4 仿真结果与分析

4.1 仿真条件

文中所采用的仿真轨迹如图4所示。起点的经纬度和高度为:116.11°E、40.05°N、5 000 m。初始俯仰角、横滚角和航向角分别为:0°、0°、30°。初始速度为200 m/s。AB段为S型转弯,飞行时间60 s;BC段匀速平飞,飞行时间120 s;CD段U型转弯,飞行时间90 s;DE段匀速平飞,飞行时间240 s。

主惯导数据由轨迹发生器直接得到。在主惯导基础上,考虑到主、子间安装误差角、挠曲变形角,并叠加器件误差后得到子惯导的实际数据。子惯导陀螺仪常值漂移和随机漂移均为0.1°/h,加速度计常值零偏和随机零偏均为100 μg,安装误差角为ξ=[1°,1°,1°]T,挠曲变形角在3个轴向上的方差为[0.2°,0.5°,0.2°]T,相关时间均为30 s。子惯导姿态误差初值为[1°,2°,3°]T,子惯导解算周期为10 ms,滤波周期为50 ms。

4.2 结果分析

仿真得到的姿态误差估计曲线如图5～图7所示。图中实线表示未补偿杆臂效应时的姿态估计误差,虚线表示补偿了杆臂效应后的姿态估计误差。从图中可看出,经过补偿后,姿态误差明显减小。在完成S型转弯后(60 s)的误差统计结果如表1所示。无论是均值还是均方根误差(RMSE)均得到了明显的改善。尤其是对于航向角,其误差均值由-7.8′减小到了-3.8′。

表1 姿态误差统计结果

5 结论

文中针对机翼挠曲变形影响下的杆臂矢量变化,详细推导了杆臂效应的产生机理,并提出了一种改进的杆臂效应动态补偿方法。与传统方法相比,该方法中杆臂矢量不再是一常值,而是随着挠曲变形不断变化。在此基础上,结合“速度+姿态”匹配传递对准模型对文中所提出的方法进行了验证。仿真结果表明,在补偿杆臂效应后,子惯导姿态误差估计精度明显提高,同时该方法也便于工程实现。