卡尔曼弹道滤波状态初值的最优估计方法研究*

范 旭,陈国光,白敦卓,朱宜家

(1 中北大学机电工程学院,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)

0 引言

对于弹道测量,其测量数据中包含着干扰或噪声引起的误差,直接用测量数据进行分析计算将会带来很大的误差,甚至是错误,而必须从量测数据中滤取所需要的信息,这种数据处理方法称为滤波。目前工程技术中使用较多的是最小二乘滤波、最大似然估计和卡尔曼滤波,其中卡尔曼滤波在控制领域,在火箭、炮弹、导弹弹道和飞行状态以及卫星轨道观测的数据处理上得到广泛的应用。卡尔曼最初提出的滤波基本理论只适用于线性系统,并且要求量测也必须是线性的[1]。如果模型是非线性的,通常在推导滤波方程时,增加线性化步骤。在状态估计时,对系统方程在前一状态值处做实时的线性泰勒近似;在预测步骤中,对量测方程在相应的预测位置也进行线性泰勒近似;所得到的卡尔曼滤波被称为扩展卡尔曼滤波。处理非线性模型的这一思想是很自然的,且滤波过程简单有效。

常规的滤波初值选取方法虽然可使滤波过程及结果收敛,但滤波前期的残差较大且滤波收敛速度慢,需要计算一段时间才可应用,影响弹道修正的实时应用并且使修正过程出现不必要的大幅度修正。为解决此类问题,需提出较好的状态初值估计方法,使滤波过程快速收敛满足弹道修正的实时性需要。

1 外弹道滤波模型

弹道滤波即是根据在一段弹道上测得的弹箭飞行弹道数据(坐标,速度、加速度、姿态角和姿态变化率),利用数学方法从这些数据中提取当前飞行状态及弹道数学模型中的参数的最优估计。而弹道预测则是利用这种最优估计和弹道数学模型计算弹道,求取在所需点的弹道参数。弹道滤波是弹道预测的基础,而弹道预测是弹道修正的重要依据,所以滤波的收敛速度及准确度也是弹道修正的重要研究方向。

1.1 滤波状态模型

地面炮位侦察雷达对空中飞行的弹箭进行跟踪和探测,地面计算机对雷达实测到的弹道参数进行数据处理,获得较准确的弹道参数,与目标坐标比较,得到弹道偏差,并由雷达向弹载计算机传输指令,使修正控制机构实现一维或二维弹道修正。根据上述弹道修正弹的执行过程,在雷达量测数据的滤波的过程中,需要用到弹道模型,考虑弹道参数获取的快速性、实时性等,文中采用质点弹道模型作为弹道滤波的状态方程[2]:

(1)

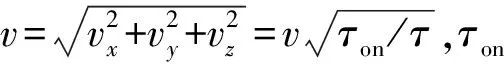
则有系统状态方程:

(2)

式中:W(k)是均值为零的高斯白噪声,且服从方差为Q的正态分布,W～N(0,Q)。

1.2 滤波量测方程

设雷达测量值为斜距r、方位角β和高低角ε,雷达坐标系为球坐标系,可得雷达测量值与地面坐标系的关系[3]:

β=arctan(z/x)

(3)

令:量测变量为Z,即Z=(r,β,ε)T,则得量测方程为:

(4)

式中:V是雷达的量测噪声,假定为零均值高斯白噪声,且服从方差为R的正态分布。即V～N(0,R),h(X)为三维矢量函数。

2 卡尔曼弹道滤波方程

卡尔曼滤波方程组分为两大部分,第一部分为卡尔曼滤波方程,这一部分负责向下一时刻推算轨迹状态;第二部分为卡尔曼滤波器的增益矩阵递推公式,这一部分用于反馈先验估计,并对预测进行修正[4]。

设k时刻的被估计状态Xk受系统噪声W驱动,驱动机理由下述状态方程描述

Xk=Φk/k-1Xk-1+Γk-1Wk-1

(5)

量测方程:

Zk=HkXk+Vk

(6)

式中:Φk/k-1为tk-1时刻的一步转移矩阵;Γk-1为系统噪声驱动阵;Hk为量测阵;Vk为量测噪声序列;Wk-1为系统激励噪声序列。

状态的一步预测

(7)

量测预测方程:

(8)

(9)

滤波增益:

(10)

一步预测均方误差矩阵:

(11)

估计均方误差

Pk=(I-KkHk)Pk/k-1

(12)

3 滤波初值的选取方法

工程运算中,对于滤波初值的选取一般为滤波时刻的量测数据,而协方差矩阵P0也是基于量测误差和时间间隔T所计算得出,进而形成主对角线矩阵[5-7]。设滤波开始时间为t,将量测数据rt,βt,εt转化为x,y,z3方向数据即xt,yt,zt。而vx,vy,vz可根据时间间隔T与xt,yt,zt。由式(3)得到。

(13)

此种方法存在较大的弊端:首先这种实时应用的初值具有较大的随机性,量测值受量测误差和系统误差影响,使位置状态初值以及计算速度的结果存在波动,及每次量测的状态初值均不相同使每次滤波过程不尽相同存在偶然性,不能满足实时性应用的要求。其次,这种求得速度初值的方法所得到的速度分量与实际弹道诸元相差较多,进而使协方差矩阵P0的数值过大,影响滤波收敛的快速性。针对这两类问题,提出如下方法。

3.1 滤波初始状态中速度分量与位置分量的估计方法

在实际情况下,弹体在空中的运动受到重力,空气阻力及横风等外界因素影响,其运动轨迹为曲线[8]。分析真实的弹道曲线,可发现弹道曲线形状与变化规律与抛物线类似,从实际情况与模型的相似性出发,可选择多项式进行曲线拟合。从上述两点分析,将采用线性回归模型进行弹道拟合并分析。在曲线拟合的计算过程中,常用到最小二乘法,高斯消去法,三次样条法和追赶法等方法,来对系数矩阵进行求解,进而得到多项式系数。基于弹道曲线的形状和拟合弹道多项式计算的快速实时性,选取最小二乘法进行进行弹道多项式拟合。

设拟合多项式的为n次幂多项式,其表达形式为

f(x)=A1·xn+A2·xn-1+…+An·x+An+1

(14)

取m次量测数据(xi,yi)(m>n),根据最小二乘法估计准则可得目标函数:

(15)

因目标函数为实际问题,其极小值必然存在,由极小值存在条件:

(16)

将上述条件方程转化为矩阵表达形式如下:

(17)

即:AX=b。

由数值分析方法可知,当系数矩阵A非奇异时,则上式有唯一解向量X。X向量中的参数就是多项式各次幂的系数。将拟合数据中xm=t代入完整多项式就可估计出滤波时刻弹箭所在的位置分量x,y,z。在已知完整多项式的情况下,对所在时刻的速度v估计应为所在时刻的多项式导数,即当x=xm时所对应的f′(xm)。

多项式f(x)的导数f′(x)表达式为:

f′(x)=nA1·xn-1+(n-1)A1·xn-2+…+An

(18)

将xm=t代入,便可获得滤波的速度分量估计初值vx,vy,vz。所以根据多项式拟合得到的曲线方程,代入滤波起始时间就可估计出弹箭所在的位置分量,进而求得速度分量,便可以此作为滤波分量的估计初值x,y,z,vx,vy,vz。

4 仿真校验

为验证此种初始状态选取方法的可行性和实用性,需进行计算机仿真计算。以某型火箭弹为例,通过6D弹道方程求解出弹道数据,将弹道数据转化为极坐标的雷达量测数据。并通过随机发生器产生均值为零的高斯白噪声作为要引入的雷达噪声,加入到原始量测数据,产生受噪声影响的雷达量测数据。

仿真计算中,取雷达数据刷新间隔为0.1 s,径向距离上的方差σr为10 m,方向角的噪声方差σr为0.001 5 rad,俯仰角的噪声方差σr为0.001 5 rad,即量测噪声矩阵R的主对角元素值。模拟在火箭弹发射3.5 s后雷达开始跟踪目标测量,在量测数据40 s,开始对弹道数据进行滤波处理,持续监控20 s左右至60 s时停止滤波处理。

多项式的拟合精度受拟合数据点个数及拟合模型与实际轨迹契合度等方面影响。所以将从采用数据点的时间长度,多项式阶数两方面来分析其变化对所估初值精度的影响。

图1可看出所估位置的残差随着拟合多项式阶数的增加先减少而后略有增加。虽然拟合数据时间长度不同,但一次多项式基本对应残差最大值,造成这种情况的原因在于直线模型与真实3方向轨迹情况存在很大差异,具有较大的模型误差,估计效果差。由一次多项式至二次多项式时,残差变化较大,证明拟合模型与真实轨迹状况的匹配度较高,估计残差速度减小。由二次多项式至五次多项式时,估计残差却略有增长。原因在于拟合数据是带有量测噪声的弹道测量数据,随着多项式阶数的增加,在拟合过程中数据点对拟合结果的影响将增大,也就是将量测噪声所引起的误差逐渐加入到了估计结果中,使得估计位置残差略有增长但较为平缓。由图2可知,随着拟合数据时间长度的增加,所估速度残差趋势基本为先减小后升高,在二次多项式的拟合模型下,所估速度残差最小并且数据长度为3 s和1 s时,基于二次多项式的速度估计残差变化不大。基于精度考虑,将选取二阶多项式作为拟合模型。

图3中可看出随数据点数的增加,基于二次多项式的估计残差逐渐减小,而到使用滤波前5 s数据时残差却有所增长。其原因在于,当数据时间长度在1 s和4.5 s之间时,随着数据点的增多,真实弹道与抛物线的相似度逐渐提高,使模型误差逐渐减小,残差随之下降。但真实弹道虽与抛物线相似,但其轨迹为非对称性,并不是二次多项式完全契合的抛物线,所以当数据时间长度再次增加时,这种差异性会逐渐凸显,造成残差增大。所以拟合数据时间长度选取为4.5 s。

从图4-图6可看出应用多项式法估计状态初值与量测数据直接应用相比,其3方向上滤波前期的残差幅值大幅度缩减,滤波收敛速度增加,残差波动平缓,证明此种方法具有较高的实用性和精度。

5 结论

文中针对雷达量测的火箭弹弹道数据,通过对滤波前期的量测数据进行坐标转换,对所量测的3个方向数据进行多项式拟合,进而估计滤波起始时刻的位置分量与速度分量,以其作为滤波初始状态。选取滤波前期拟合数据长度和拟合多项式阶数作为变量,通过计算机仿真分析其对弹道参数估计精度的影响,最后选取最优组合确定其为滤波初始状态估计的最优方法。通过滤波仿真,验证此种初始状态选取方法的可行性。由仿真结果可看出,量测数据直接应用后,3个方向滤波收敛时间在滤波开始后5.5 s左右,而应用此种估计方法的滤波过程基本在2.5 s收敛,滤波收敛时间减少一半且滤波幅值大幅度减少,满足快速准确的要求,具有实用性应用。