基于Bayesian-Fisher混合模型改进的交互式多模型算法*

包守亮,程水英

(电子工程学院,合肥 230037)

0 引言

长期以来,机动目标跟踪是跟踪领域研究的热点和难点[1-2]。经过半个多世纪的研究,较为典型的算法模型主要有:变维滤波(variable dimension filter,VDF)、Singer模型、Jerk模型、CS模型以及多模型(multiple model,MM)算法。由于目标的机动特性未知,采用单一模型通常难以全面准确的描述目标的运动状态,多模型算法则较好地弥补了这一缺陷,其中以IMM算法应用最广。IMM算法由多个模型并行滤波,通过交互,对各滤波器的输出进行概率加权,通常被认为是最有效的混合估计方式[3-4]。

由于目标机动特性未知,要提高跟踪精度,必须增加模型数量以覆盖其可能存在的各种机动状态。然而,过细的建模可能会破坏Bayesian推理的完备性和模型的独立性,造成模型之间的过分竞争,反而降低跟踪精度[5-6]。传统的IMM算法主要基于匀速(CV)、匀加速(CA)、协同转弯(CT)设计模型集,如:CVCA[7]、CVCT[8]以及CVCACT[9]。随着目标机动能力的提升,又提出利用相关噪声模型与CV模型进行组合,如:CVCT-Singer[10],CVCS[11-12]等。然而相关噪声模型通常是基于Bayesian准则下的模型自适应算法,存在对初始参数依赖性强,对不确定状态鲁棒性差的缺陷。鉴于此,Khaloozadeh等将Fisher方法与Bayesian方法进行有机融合,提出了Bayesian-Fisher混合模型[13-14]。

文献[15]基于Bayesian-Fisher混合模型对匀加速模型进行改造,提出了修正的输入估计算法(modified input estimation,MIE)。文献[16]将MIE与强跟踪算法结合,融入概率密度假设滤波器,用于多机动目标跟踪。文献[17]将强跟踪MIE算法与CV组合,作为IMM算法的模型集,取得了优异的跟踪效果。考虑到匀加速模型的结构是固定的,不能随着目标机动进行自适应调整。因此,文中提出利用Bayesian-Fisher混合模型对相关噪声模型(CS)进行改进,并基于类似的原理改进CV模型,并在IMM算法的框架进行交互,用于跟踪机动目标。通过两个连续机动场景验证了算法的有效性。

1 Bayesian-Fisher混合模型

Bayesian模型是一种常用的不确定性模型,其模型的不确定性来源于将噪声以及相关参数作为随机过程进行建模(如卡尔曼滤波器认为过程噪声v、量测噪声w为零均值白噪声序列;机动目标跟踪中,将未知的加速度作为马尔可夫或半马尔可夫过程进行建模),但是这种不确定性通常又可以由初始设定的参数值或统计特征来确定(如高斯噪声可以由其一、二阶矩精确描述),造成基于Bayesian模型的自适应滤波算法对初始参数依赖性强,在目标状态与初始参数不匹配时,滤波精度显著下降。Fisher模型通过对模型中的部分不确定性因素进行实时估计,可以较好地解决上述问题。

对于机动目标,假设其离散状态方程与量测方程可表示为:

(1)

式中:Fk为状态转移矩阵;Gk为输入控制矩阵;Γk为过程噪声分布矩阵;Hk+1为量测转移矩阵;uk为机动输入项;vk、wk分别为零均值的白色过程噪声和量测噪声序列,其协方差矩阵为Qk和Rk,且任意时刻的vk与wk不相关。由于Fk、Gk、Γk、Hk+1通常为时不变矩阵,故省略时间下标,简记为F、G、Γ、H。

由于机动输入项uk未知,故将其增广到状态向量中进行实时估计,把状态方程改写为:

(2)

同时,对量测方程进行改写:

zk+1=Hxk+1+wk+1=

H(Fxk+Guk+Γvk)+wk+1=

(3)

(4)

E[(HΓvk+wk+1)(HΓvk+wk+1)T]=

HΓQkΓTHT+Rk+1

(5)

至此,便建立了完整的Bayesian-Fisher混合模型。该模型通过将未知的机动输入项uk增广到状态向量中进行实时估计,削弱了模型的不确定性,增强了算法的鲁棒性。同时,不难发现,式(4)与标准的卡尔曼滤波形式相同,因此,可以在线性卡尔曼滤波器框架下进行最优Bayesian估计。

2 改进的当前统计模型及匀速模型

2.1 当前统计模型及其改进算法

当前统计模型采用修正的瑞利分布描述机动目标加速度的统计特性,认为目标机动时,下一时刻加速度的变化范围有限,只能在当前加速度的邻域内。以一维空间为例,CS模型的离散状态方程为:

(6)

(7)

(8)

(9)

(10)

step1 时间更新

(11)

(12)

step2 量测更新

(13)

(14)

式中:

(15)

(16)

(17)

2.2 匀速模型及其改进算法

匀速模型又称非机动模型,常与机动模型组合,用于IMM算法的模型集设计。其状态方程及量测方程可表示为:

(18)

为将其统一到Bayesian-Fisher混合模型的框架中,需要对CV模型进行相应的改写。由于其状态方程不涉及未知输入项,因此,对状态方程不做处理,只对量测方程按式(3)进行改写。改进后的CV模型状态方程及量测方程为:

(19)

3 基于Bayesian-Fisher混合模型改进的IMM算法

IMM算法由多个滤波器并行滤波,通过概率加权得到最终输出结果,是一种效费比高、性能优异的结构自适应算法。但是其包含的各个滤波器又是基于模型的,最终融合输出结果的好坏,更大程度上取决于各滤波器跟踪性能的优劣。因此,对模型集的设计尤为重要。过少的模型不能全面覆盖目标的机动特征,容易导致模型失配;过多的模型会造成模型间的过度竞争,增加算法复杂度,降低效费比。一种较好的设计方式是将相关噪声模型与匀速模型相结合,通过CV对非机动状态跟踪的高精度以及相关噪声模型对机动状态的自适应调整,达到对目标运动状态的全面覆盖,取得较高的跟踪精度。因此,文中将改进的CS模型(MCS)以及改进的CV模型(MCV)相结合,提出基于Bayesian-Fisher混合模型的IMM算法,简记为IMM-BF。

IMM算法是递推进行的,一个完整的递推过程包含四个步骤,即模型条件重初始化、模型条件滤波、模型概率更新和估计融合。

step1 模型条件重初始化

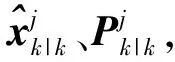
(20)

(21)

(22)

式中：上标i或j代表第i或第j个模型,下同,i,j∈{1,2,…,r}。

step2 模型条件滤波

由步骤1得到k+1时刻MCS和MCV子滤波器的初始状态和协方差后,两个滤波器均依据式(11)-式(17)的滤波步骤进行递推更新。

step3 模型概率更新

(23)

(24)

step4 估计融合

(25)

(26)

4 仿真校验

为充分测试算法的有效性,选取两种典型的连续机动场景,利用IMM-CVCA、IMM-CVCACT、IMM-CVCS、IMM-CVSTMIE[17]以及文中提出的IMM-BF算法分别进行跟踪。采用均方根误差(root mean square error,RMSE)作为性能评价指标,各场景下Monte-Carlo仿真100次。

4.1 仿真实验一

假设目标在二维平面内运动120 s,初始位置z0=[10000 m,2000 m]。分别在0～20 s、40～60 s、110～120 s进行匀速运动,vx=-160 m/s,vy=50 m/s,20～40 s、60～80 s进行转弯机动,角速度分别为π/18 rad/s、-π/20 rad/s,80～110 s进行匀加速运动,ax=ay=5 m/s2。

参数设置:各算法均采用三点初始化,量测噪声协方差R=diag(1002,1002),过程噪声协方差为:

利用文中提出的IMM-BF算法以及上述的四种算法对目标进行跟踪,其位置、速度均方根误差曲线如图1、图2所示。同时,对观测时间内的平均均方根误差以及稳定后(20 s以后开始统计)的峰值误差进行统计,结果由表1给出。

表1 各算法跟踪性能比较

由图1、图2以及表1易知,在非机动段,各算法均能取得较好的跟踪效果,而在机动段,跟踪误差迅速上升。但总体上讲,基于Bayesian-Fisher混合模型框架下的文中算法IMM-BF以及文献[17]的IMM-CVSTMIE算法具有更高的跟踪精度和更低的峰值误差,且对状态变化的响应速度更快。其原因在于,将未知的机动输入进行在线实时估计,使得子滤波器在目标状态改变时能及时进行调整,减小了模型失配。而相比文献[17],文中通过对CS模型的改进,一方面提高对加速度均值的估计精度,使模型与实际运动更加匹配,另一方面保留了CS模型对机动的自适应调节能力。因此,文中算法具有更强的机动适应能力。这一点可从图2中在目标进行转弯运动时看出,由于IMM-CVSTMIE其本质是一种改进的IMMCVCA算法,不能很好地匹配转弯运动,因此其跟踪精度有所下降。

4.1 仿真实验二

选择文献[19]中的机动场景来测试文中算法的有效性。这些机动场景被广泛用于测试多模型算法的稳态误差、峰值误差、以及响应速度[19-20]。目标初始状态为x0=[8 000 m,25 m/s,8 000 m,2 000 m/s],然后按照表2所示的加速度跳变进行机动。

表2 目标机动跳变过程

仿真条件不变,仍利用上述算法对目标进行跟踪,图3、图4分别为位置、速度均方根误差曲线。

对仿真场景二的跟踪结果与仿真场景一类似,进一步验证了文中算法在各种机动场景下的实用性。无论是机动还是非机动段,文中算法均取得了更高的跟踪精度。尽管目标机动时,误差迅速增大,但是相比同类算法,其收敛速度更快,峰值误差更小,这都得益于对未知机动输入的实时估计。

一个好的跟踪算法要应用于工程实际,除具有较高的跟踪精度外,还必须考虑硬件条件的限制,如算法的计算复杂度。文中通过单次Monte-Carlo仿真所需的平均时间来评价各算法的计算量。在处理器Intel(R) Core(TM) i3-2350 CPU @ 2.3 GHz,RAM为4 GB的计算机上采用Matlab2014做500次Monte-Carlo仿真实验,两种场景下,各算法单次实验的平均用时如图5、图6所示。

仿真结果表明,两种场景下各算法相对耗时是一致的,场景二目标运动时间更长,因此单次仿真耗时更多。容易看出,IMMCVCA、IMM-CVCS具有最好的实时性,但是其跟踪效果比较差。IMM-CVCACT通过增加模型集,性能有所提升,但实时性最差。IMM-CVSTMIE由于引入了强跟踪因子,而强跟踪因子的计算量约为相应卡尔曼滤波算法的1/3[21],因此,其计算量接近三模型交互的IMM算法。而文中算法尽管扩维时增加了一定的计算量,但是不及文献[17]的IMM-CVSTMIE,其跟踪精度却是所有算法中最高的,故文中提出的IMM-BF算法是一种性能优异、效费比高的多模型算法

5 结论

通过引入Bayesian-Fisher混合模型对CS模型以及CV模型进行改进,并将改进的CS、CV用于IMM算法的模型集设计。借助CV对非机动状态的高精度跟踪,以及MCS对机动状态的快速自适应调节,在没有任何先验信息的条件下,文中改进的IMM算法不仅具有较好实时性,而且相比其他通用型机动跟踪算法精度更高,具有一定的工程实际价值。