基于GPS/地磁组合弹体滚转姿态测量方法
2018-11-09袁丹丹李新华易文俊
袁丹丹, 李新华, 易文俊, 管 军
(1. 南京理工大学瞬态物理国家重点实验室, 江苏 南京 210094; 2. 西北工业集团有限公司, 陕西 西安 710043)
0 引 言
弹丸姿态信息测量的准确与否将在很大程度上影响弹丸制导控制系统的性能,因此,准确获取弹体的飞行姿态对制导控制系统的可靠性、精确性、快速性具有重要的意义。目前,在弹丸姿态测量的方法中,惯性测姿方法是常用的技术手段,但该方法存在误差累积等缺陷[1-5]。且对于声管发射的制导炮弹,其具有高动态、高发射过载、高转速等特点,惯性器件难以满足上弹应用要求[6]。磁阻传感器[7-8]可测量与磁场强度有关的参数,且计算误差不随时间累积,并具有体积小[9-10]、成本低和抗高过载等优点,在姿态测量领域中得到了广泛的应用[11-12];根据地磁场特性,地磁强度和方向是位置的函数[13],由国际地磁参考场(international geomagnetic reference field,IGRF)计算得到我国地磁场总量在各处变化较小或基本相等。由相关文献可知经纬度每变化1°,地面距离大概变化110 km,目前声管发射武器的射程基本在100 km以内,故可认为在弹丸的射程范围内,当地磁场的大小和方向基本不变。此外,全球定位系统[14-17](global positioning system, GPS)具有全天候、高精度、连续定位等优点,可为弹体实时提供时间、位置和速度等信息。若单独采用某一种方法进行姿态测量,均会受到自身条件的限制从而影响测量精度,因此国内外很多学者对组合测姿方法进行了大量的研究,如GPS/加速度计组合、磁/陀螺仪组合等[18-22]。
结合GPS和磁阻传感器的特点,本文对GPS/地磁组合测姿方法进行了相关研究,利用GPS提供的速度信息进行弹道倾角和偏角的解算,再结合地磁输出信息进行弹体滚转姿态测量求解。文献[23]建立了以俯仰角为误差的仿真模型,进行了系统误差计算,在排除了某一区域的情况下,验证了该组合测量弹体滚转角的可行性,故而在忽略磁探测过程中可能出现的磁盲区的影响,该组合不失为一种有效的弹体滚转姿态测量解算方法。本文在GPS/地磁组合测量方法的基础上,对地磁测量盲区问题进行了研究分析。针对可能出现的磁盲区的情况提出了解决方法,建立了相应的解算模型,根据GPS输出的速度信息估算出加速度,进行速度倾斜角的解算,用于在磁盲区情况下出现滚转姿态解算不准确时进行替代,并对采用弹丸的速度倾斜角代替滚转姿态输出的可行性进行了理论验证。通过6自由度外弹道计算仿真验证了该解决方法的可行性,有效地弥补了磁阻传感器在地磁测量盲区出现时组合滚转姿态解算误差较大或无法解算不足,提高了GPS/地磁组合弹体滚转测量姿态解算的精度。
1 GPS/地磁组合测量弹体滚转姿态
1.1 组合测量原理


表1 地面坐标系与弹体坐标系之间的方向余弦表
本文中磁阻传感器捷联安装在弹体上,其敏感轴方向与弹体坐标系一致,因此当弹丸在空中运动时,磁阻传感器可以敏感到弹体3个轴上的地磁数据。记地磁场强度矢量B在地理坐标系oNED(北东地)下的地磁分量分别为BNx、BEy、BDz,用Bx、By、Bz表示其在地面坐标系三轴上的投影,用Bx1、By1、Bz1代表其在弹体坐标系下的分量。用φ描述地面坐标系ox轴与地理坐标系oN轴之间的夹角,向东偏为正方向。结合当地地磁场矢量和磁阻传感器的输出,由坐标系之间的转换关系可得
(1)
在弹丸发射时,夹角φ是确定的已知参数。为方便计算文中取地面坐标系ox轴沿地理坐标系oN轴,即φ=0,将式(1)整理简化可得
(2)


(3)

1.2 磁探测盲区分析
作为地球的基本场,地磁场属于地球的固有资源,地球表面任意点的磁场都可以通过地磁场强度表示,均由地磁要素确定,这为导航提供了良好的外部基准。根据我国各地的地理位置信息:经度、纬度和高度,通过世界地磁模型(world magnetic model,WMM)可查得该地的3个地磁要素:北东地3个方向上的地磁分量BNx、BEy、BDz,磁偏角D和磁倾角I由如下公式计算得到,即
D=arctan(BEy/BNx)

(4)
在弹丸飞行过程中,安装在弹体y1轴和z1轴向的磁阻传感器的输出是取决于地磁场强度矢量与弹体轴两者的位置关系的。当在飞行过程中出现弹体轴与地磁场强度矢量平行或接近平行时,那么地磁强度矢量在弹体纵向面的投影为0,此时磁阻传感器的敏感轴在纵向面上的输出只有噪声,将会导致滚转解算结果不可信。也就是说在弹丸的某一段飞行过程中会出现这样的情况,以地磁强度矢量为中心的小范围内,磁阻传感器的敏感轴输出为0或者很小,根据GPS/地磁组合方法无法进行滚转姿态的解算或者解算误差很大,被称之为磁探测盲区。本文分两种情况对磁盲区情况进行分析,具体如下。
(1) 在出炮口之际,分析出现磁盲区的情况
当地磁强度矢量恰巧位于射击平面oxy内,对于D<0时,φ=D或φ=D+π;对于D>0时,φ=D或φ=D-π。此时地磁强度矢量在地面系侧向轴分量为0,即BDz=0。
对于I>0,在φ=D+π或φ=D-π时,若射角为I时,则弹体轴与地磁强度矢量近乎重合,此时基于GPS/地磁组合的滚转姿态解算方法出现了局限性。
对于I<0,在φ=D时,若射角为-I时,则弹体轴与地磁强度矢量近乎重合,此时基于GPS/地磁组合的滚转姿态解算方法出现了局限性。
(2) 在弹丸飞行中,分析出现磁盲区的情况
在地面系与地理系的关系确定后,地磁强度矢量与地面系之间的关系用两个角度来描述,记地磁强度矢量与水平面oxz间的夹角为磁俯仰角θI,指向水平面上方为正,θI=-I。记地磁强度矢量在水平面的投影与地面系ox轴之间的夹角为磁偏航角ΨD,左偏为正,ΨD=φ-D。在飞行过程中,当弹丸的俯仰角、偏航角与磁俯仰角、磁偏航角非常接近或绝对值互补时,即弹体轴与地磁强度矢量平行,此时基于GPS/地磁组合的滚转姿态解算方法将无法解算弹丸的滚转信息。当弹体轴与地磁强度矢量不在同一条直线,但是存在较小的夹角时,也会带来较大的滚转角解算误差。
因此若弹体恰好处在磁测量盲区时, 通过GPS/地磁组合测量弹丸滚转姿态将会具有较大的误差。根据在出炮口之际出现磁盲区的情况分析,在允许的范围内可以对射角射向进行合理的选择来有效地避免出炮口磁盲区的出现;而对在弹丸飞行过程中出现磁探测盲区的情况,提出了利用GPS输出信息进行速度倾斜角(伪滚转姿态)的解算来弥补GPS/地磁组合无法解算滚转姿态或者解算误差较大的缺陷,建立了相关的解算模型,并对采用弹丸的伪滚转姿态代替滚转姿态输出的可行性进行了理论验证。
1.3 弹体轴与地磁强度矢量夹角的计算

2 GPS伪滚转姿态解算

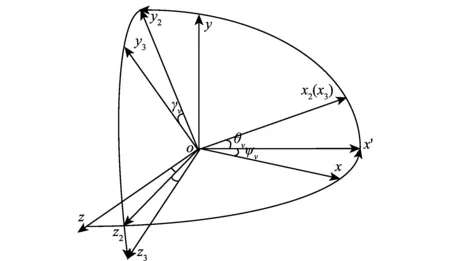
图1 3个坐标系之间的关系Fig.1 Relations between three coordinate systems
2.1 伪滚转姿态的解算原理
伪滚转姿态角描述的是弹道坐标系跟速度系之间的关系,位于包含速度v的铅垂面oy2z2内,也在垂直于速度的oy3z3平面内。通过计算oy3z3平面内的升力与oy3轴的夹角,以及与oy2轴的夹角,由几何图形分析可知伪姿态角即为上述两个夹角之差。
用i、j、k分别表示北东地坐标系3个轴向的单位矢量,那么弹丸在北东地坐标系下的速度分量和加速度分量可分别表示为v=vNxi+vEyj+vDzk和a=aNxi+aEyj+aDzk。加速度信息可以通过GPS输出得到的速度信息(vNx,vEy,vDz)进行估算得到,此处以北向加速度为例说明。记k时刻和k+1时刻的速度为vNx(k)和vNx(k+1),则k+1时刻的北向加速度为aNx(k+1)=(vNx(k+1)-vNx(k))/(tk+1-tk)。伪滚转姿态的解算步骤如下。
步骤1速度坐标系oy3z3平面内的加速度分解


法向加速度an以及法向重力加速度gn都位于垂直于速度的纵向平面oy3z3内,而法向加速度an则是由gn跟另一矢量(记为l)合成的总法向加速度,故矢量l=an-gn。
步骤2速度坐标系oy3z3面内合力的方向解算
由外弹道理论可知,弹丸在飞行过程中由于攻角的存在,使得其速度方向与弹体轴的方向是不重合的,则总的空气动力不仅包含沿速度反方向的阻力,还有垂直于速度方向的升力,位于速度坐标系oy3z3平面内,由牛顿第二运动定律可知升力方向与加速度矢量l的方向是一致的。将升力fy3z3在oy3z3平面内分解到oy3轴和oz3轴上,记为fy3和fz3,如图 2所示。
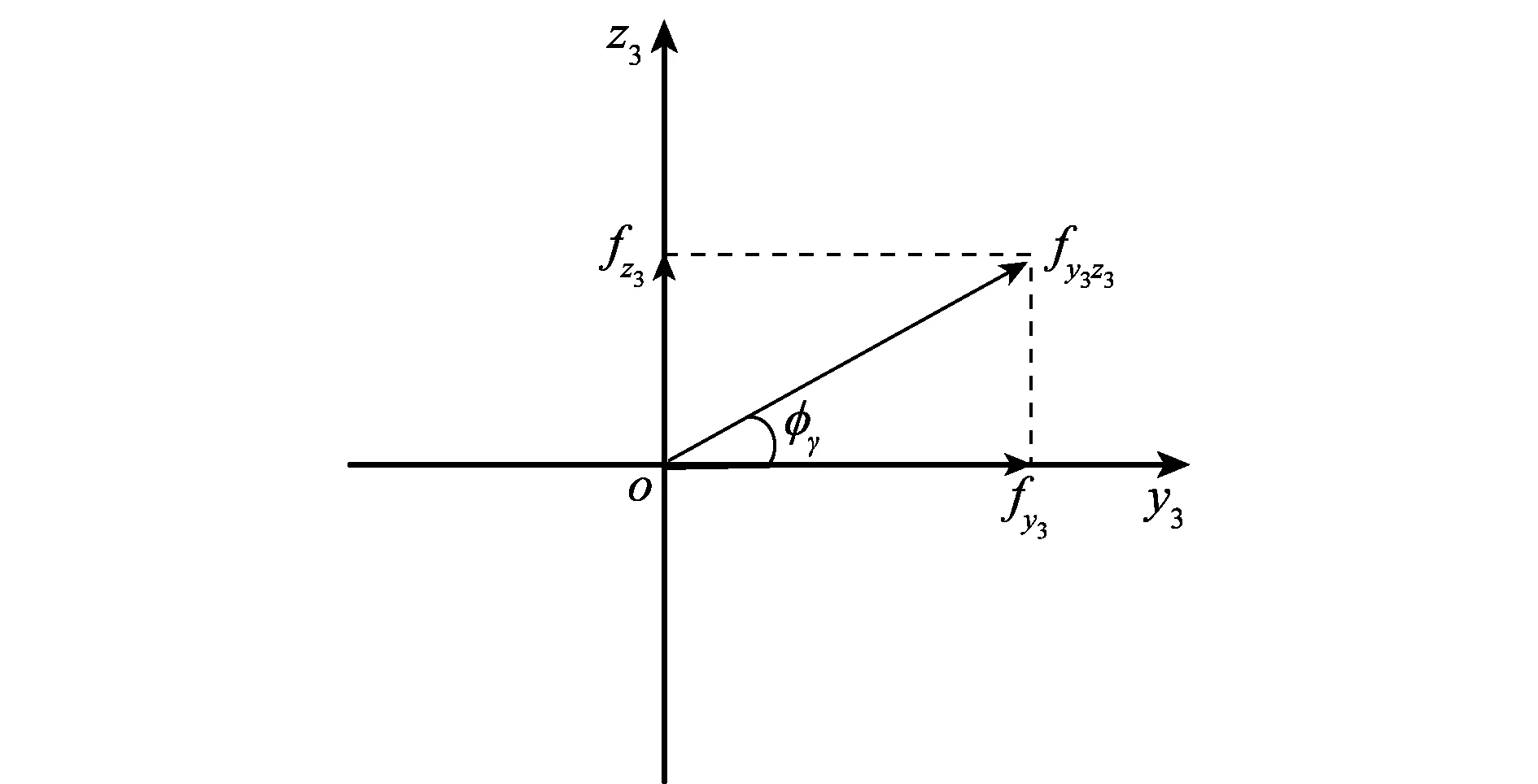
图2 速度系纵面oy3z3内升力的分布Fig.2 Distribution of lift in longitudinal plane oy3z3
计算升力与oy3轴两者之间的夹角φγ,解算如下,其中升力由文献[25]给出的方法计算得到,即

步骤3构建水平参量
由重力加速度矢量和速度矢量之间的关系,可以构造出水平参照矢量p,记p=g×v,该矢量位于水平参照面内,方向沿弹道坐标系的oz2轴方向,如图 3红虚线所示。

图3 水平参量方向Fig.3 Direction of horizontal parameters
步骤4矢量l与包含矢量v的铅垂面的夹角

步骤5伪滚转姿态的解算
φγ、φs、γv3个角度之间的关系如图 4所示,故伪滚转姿态γv=φs-φγ。
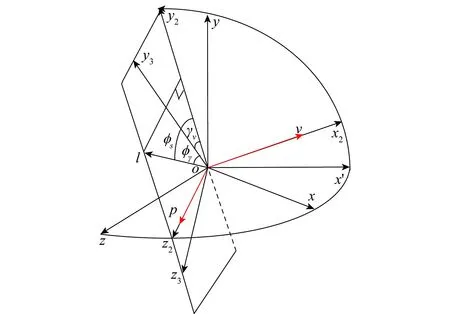
图4 3个角度之间的关系Fig.4 Relations among three angles
2.2 伪滚转姿态替代滚转角的可行性检验

sin(γv)=(cos(α)sin(β)sin(θ)-
sin(α)sin(β)cos(γ)cos(θ)+cos(β)sin(γ)cos(θ))/cos(θv)
(5)

sin(γv)≈(βsin(θv)+αβcos(θv)-αβcos(γ)cos(θv)+
α2βcos(γ)sin(θv)+sin(γ)cos(θv)-αsin(γ)sin(θv))/cos(θv)
(6)
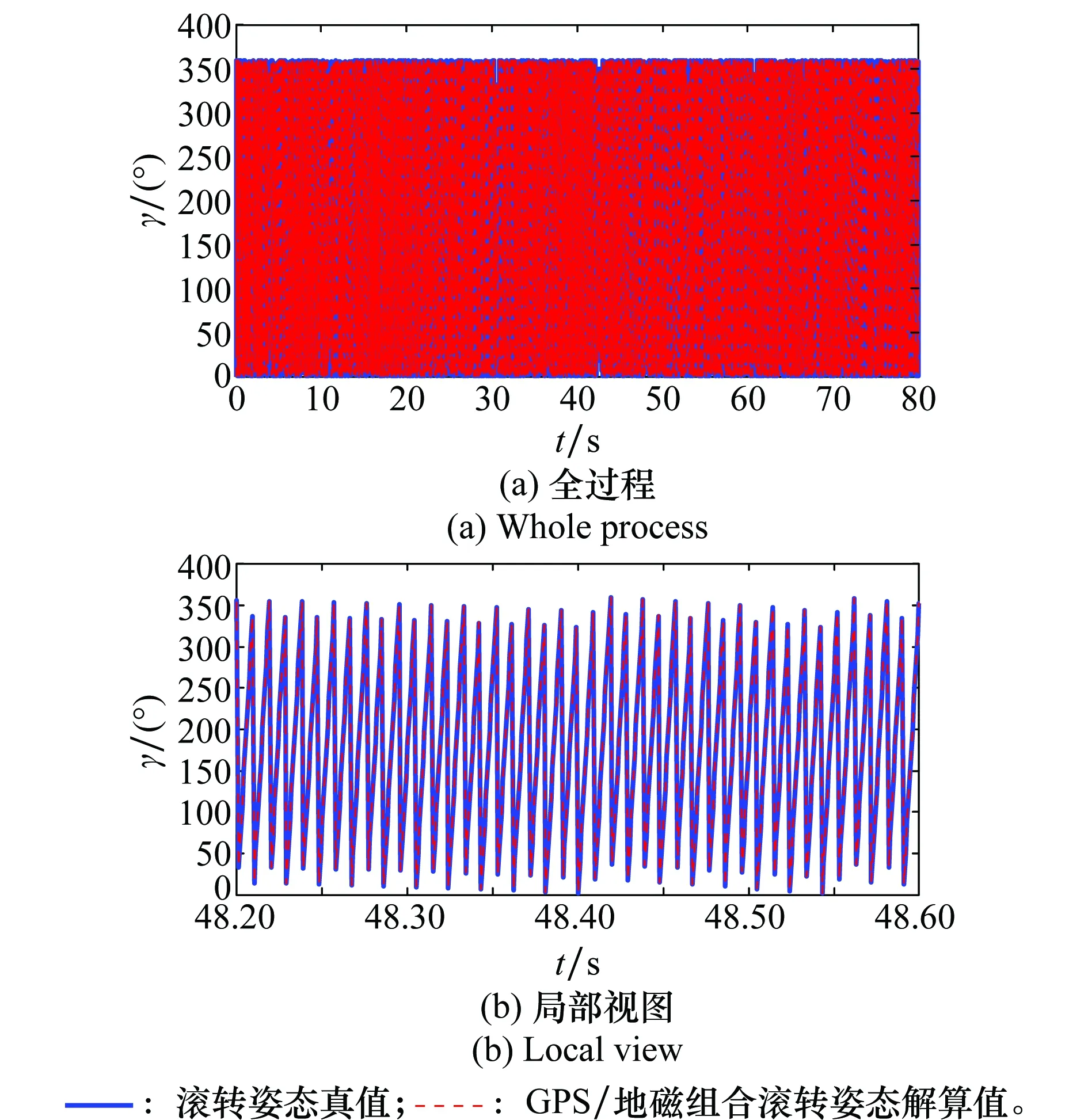
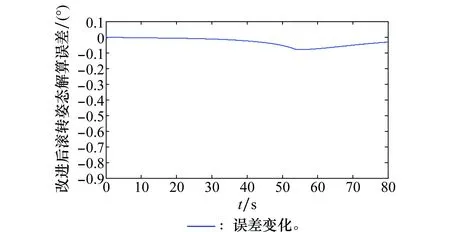
通常弹道倾角的范围为(-π/2,π/2),所以有:-1 γv)cos(θv)=sin(γv)cos(θv) α2βcos(γ)sin(θv)+sin(γ)cos(θv)-αsin(γ)sin(θv))= 所以,sin(γv)cos(θv)≈sin(γ)cos(θv),即sin(γv)≈sin(γ)。 所以,γv≈γ+2kπ或γv≈(2k+1)π-γ,k为整数。 由地面、弹道、速度、弹体4个坐标系的定义可知,同一时刻的伪滚转姿态和滚转角是处在相同的范围区间内,排除了多值的情况,所以γv≈γ,上述即为用伪滚转姿态替代滚转角的可行性验证。 针对文中所采用的GPS/地磁组合弹体滚转姿态测量方法,以及本文提出的利用GPS输出信息进行伪滚转姿态解算的方法,通过数值仿真验证其可行性。本文基于六自由度弹道模型方程进行了数值计算,模拟生成全过程弹道参数。WMM每5年发布一次,最新发布的会在2019年底到期[27],根据南京的地理位置为北纬32.028°、东经118.854°以及海拔高度24.03 m查得地磁要素BNx=32 827.3 nT,BEy=-3 153.2 nT和BDz=37 268.2 nT,通过计算得到南京的磁偏角D=-5.487°,以及磁倾角I=48.495°。 数值计算初始条件:弹丸初速v=750 m/s,初始射角θv=45°,取地面坐标系ox轴沿地理坐标系oN轴,即地面系与地理系夹角为0。根据理论弹道参数模拟GPS输出的飞行速度信息以及磁阻传感器三轴的输出信息,并进行磁探测盲区的分析。最后根据文中提出的算法进行伪滚转姿态的解算,并与滚转姿态角理论值进行比较分析,计算仿真结果如图5~图8所示。 图5给出了文中所采用方法的仿真结果与滚转姿态角理论值之间的对比关系,图5(a)是飞行弹丸全过程滚转姿态对比曲线,而图5(b)是全过程对比曲线的局部呈现,方便更清晰地看出两者的吻合程度。从图中可以看出GPS/地磁组合测量弹体滚转姿态解算的方法能有效解算出弹丸滚转角。 基于GPS/地磁组合滚转姿态解算误差曲线如图6所示,通过误差的大小来检验该组合解算滚转姿态的精度高低。 从图6可以看出,在0~54 s时,误差绝对值很小,而且误差曲线的变化很平稳,可见此段飞行过程中基于GPS/地磁组合滚转姿态解算方法的精度高;从54 s开始往后,误差绝对值在逐渐增大,并在68.8 s时达到最大;从68.8 s开始往后到飞行结束,误差绝对值又在逐渐减小,并在最后有趋于平稳趋势。 图5 滚转角姿态解算值与真实值Fig.5 Calculation result and actual value of roll attitude 图6 组合姿态解算误差Fig.6 Calculation error of the combination method 图7描述了弹体轴与地磁矢量夹角随时间的变化以及组合姿态解算误差随时间的变化。 图7 夹角变化与解算误差变化对比Fig.7 Comparition of the variation between angle and thecalculation error with time 由图7可以看出,弹体轴与地磁矢量的夹角先逐渐在减小,在68.8 s时达到最小值,从68.8 s往后到飞行结束逐渐增大。对比夹角曲线和误差曲线,从0~54 s时,夹角始终大于20°,此时组合姿态解算误差值很小且变化平稳;从54 s往后到68.8 s时,夹角逐渐减小并达到最小值,而组合姿态解算误差绝对值在逐渐增大并达到最大值;从68.8 s到飞行结束,夹角在逐渐增大,误差绝对值在不断减小。在68.8 s处,根据GPS输出的速度信息计算得到此时的弹道倾角为-48.5°,弹道偏角为-1.219°,与磁倾角和磁偏角比较可知,此时弹道倾角非常接近磁倾角,而弹道偏角和磁偏角相差不大。因此,当弹体轴与地磁矢量夹角大于20°时,此时基于GPS/地磁组合滚转姿态解算方法精度高;而当弹体轴与地磁矢量夹角小于20°时,且夹角越小,组合姿态解算误差越大;在弹道偏角与磁偏角相差不大时,若弹道倾角比较接近磁倾角,弹体轴与地磁强度矢量的夹角达到最小,此时基于GPS/地磁组合滚转姿态解算误差最大或无法解算,夹角小于20°这一区域即为磁探测盲区。此处得出夹角小于20°作为磁探测盲区的判断是根据文中仿真实验分析出来的结果,并不具有一般性。针对具体情况,可如文中所述,根据弹体轴与地磁矢量的夹角变化与组合姿态误差变化对比,进行磁探测盲区的判断。 针对磁探测盲区情况,利用GPS输出信息进行伪滚转姿态的解算替代组合解算输出,改进后滚转姿态解算误差变化如图8所示。 图8 改进后滚转姿态解算误差变化Fig.8 Variation of calculation error after improvement 由图8可以看出,改进后的弹体滚转姿态解算误差减小,提高了弹体滚转姿态解算精度。 文中在GPS/地磁组合测量方法的基础上,对磁探测盲区问题进行了研究分析。通过选择合适的射角射向,可以避免出炮口磁探测盲区的出现;在弹丸飞行过程中通过计算弹体轴与地磁强度矢量的夹角来判断磁探测盲区的出现。针对磁探测盲区的情况,建立基于GPS弹丸伪滚转姿态的解算模型,利用GPS量测信息进行伪滚转姿态的解算来弥补GPS/地磁组合无法解算滚转姿态或者解算误差较大的缺陷,并对弹丸伪滚转姿态替代滚转姿态的等价性进行了理论验证。通过六自由度外弹道仿真进行验证,从仿真结果看,基于GPS伪滚转姿态的解算方法可以有效弥补磁探测盲区出现时GPS/地磁组合方法的不足,提高了弹丸滚转姿态解算精度。此外,弹体轴与地磁强度矢量的夹角越大,基于GPS/地磁组合弹丸滚转姿态测量解算的误差越小,解算精度越高。

3 仿真验证


4 结 论
