飞行器栖落机动切换控制设计及其吸引域计算

王 月, 何 真, 张建兰, 袁 亮, 陆宇平

(1. 南京航空航天大学自动化学院, 江苏 南京 211106; 2. 航空机电系统综合航空科技重点实验室, 江苏 南京 211106)

0 引 言

与旋翼机相比,小型固定翼无人机在续航能力、飞行范围以及巡航速度等方面具有明显的优势。但旋翼机可以做到垂直起落,而固定翼无人机一般通过滑行减速、撞网和伞落等方式进行降落。这几种降落方式有场地空间需求大、地面辅助降落装置复杂和落点不确定等缺点,限制了固定翼无人机的应用场合。人类从鸟类栖落过程中发现了灵感,如果固定翼无人机能像鸟类那样实现栖落,就能突破固定翼飞行器降落条件的限制,从而扩大固定翼无人机的应用场合。我们观察金雕的栖落过程,金雕在接近目标的前一刻,迅速拉起身体、张开翅膀并且双腿前伸,这一套动作使金雕的飞行状态从平飞进入过失速状态,迅速减速并且实现精确栖落,整套动作敏捷而精准。固定翼无人机如果能模仿鸟类的栖落机动[1-5],利用大迎角产生的高阻力快速减速并实现精确地栖落,那么飞行器就可以随时随地栖落,这样无人机就能提高续航能力和提升作战性能。因此,栖落机动的研究具有重要的应用价值。

近年来,固定翼无人飞行器的栖落机动得到了越来越多的关注。文献[6]设计了一种小型滑翔机,用实验验证了固定翼飞行器栖落在电线上的可能性。文献[7]研究了变体无人机栖落机动纵向运动的多体动力学建模与仿真问题,并分析了变体结构对栖落机动性能的作用。文献[8]为栖落机动设计了一种滑模控制器。

上述文献主要讨论了栖落机动的轨迹控制器设计,没有探讨所设计控制器的局部稳定区域(即吸引域)的计算方法。对栖落机动而言,计算吸引域一方面可以确定飞行器偏离参考轨迹的容许范围,另一方面可以保证容许范围内的飞行器能够在有限时间内准确地栖落在目标区域内。因此,吸引域计算对栖落机动的实现具有重要的意义。近年来,对局部稳定的非线性系统计算吸引域的问题得到了学术界的关注。文献[9]利用线性矩阵不等式(linear matrix inequality,LMI)凸优化方法计算了Lyapunov函数,解决了光滑非线性系统的吸引域计算问题。文献[10]提出运用平方和(sum-of-squares, SOS)的方法计算局部稳定系统的吸引域。文献[11]运用基于仿真的方法计算局部稳定的系统的吸引域。与平方和最优化算法相比,这种方法更简单更直接,并且不要求系统模型是多项式形式,但是这种方法计算量大,效率较低。以SOS方法为基础,文献[12]提出了一种固定翼飞行器栖落机动控制器综合设计方法——LQR-Trees控制方法,并探讨了该方法的鲁棒性。

本文针对固定翼无人机栖落过程的非线性特性,以切换控制理论为基础展开了栖落机动轨迹控制研究,并针对所设计的栖落机动切换控制律,设计了相应的SOS优化算法,计算了吸引域。首先沿着参考轨迹将栖落机动的非线性动力学模型线性化,构造出分段线性模型;然后结合最优控制理论与切换控制理论,对分段线性系统设计切换控制律。随后针对所设计的栖落轨迹跟踪切换控制律,改进设计了SOS优化算法以计算栖落轨迹吸引域Ω。这样,只要系统的状态量X∈Ω,则在所设计的轨迹跟踪控制器的作用下,飞行器能够准确地栖落在目标区域里。最后,对固定翼飞行器的栖落机动控制过程进行了仿真验证。

1 栖落机动中飞行器的气动模型与动力学模型

以发动机的推力和升降舵的偏转作为控制输入。固定翼飞行机的纵向运动方程为

(1)

式中,V,μ,α,q分别表示飞行速度、航迹角、迎角和俯仰角速度;x和h分别表示飞行器的水平位置和高度;m是飞机的质量;Iy是转动惯量;T是推力;L是升力;D是阻力;M是空气动力矩。

飞行器的纵向空气动力和力矩为

(2)

式中,CL、CD和CM分别是飞行器升力、阻力和力矩系数;ρ是空气密度;S是飞行器的空气动力表面积。

飞行器栖落过程中的空气动力学系数由平板模型方法[13-15]得到,升力和阻力系数可由式(3)逼近。

(3)

俯仰力矩系数为

.8cosαsin(2α+2δe)+

1.4sinαsin2(α+δe)+0.1sinα)

(4)

式中,Se为升降舵的空气动力表面积;δe是升降舵偏转角;le是升降舵空气动力重心到飞行器质心的距离。

2 栖落机动轨迹跟踪控制律设计

飞行器栖落机动是迎角大范围变化的非常规机动方式,因此需要设计控制器改善飞行器的栖落机动性能,保证飞行稳定,并实现定点栖落。在设计控制器之前,需要给定一条参考轨迹,优先设计参考轨迹的目的是将飞行器定点栖落控制问题转化为轨迹跟踪问题。参考轨迹可以利用GPOPS工具箱进行设计[16-17]。本小节主要对原非线性动力学模型作线性化处理,并且结合最优控制与切换控制对处理后的线性切换系统设计轨迹跟踪控制器。

2.1 分段线性化模型

设飞行器栖落机动非线性模型为

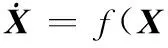
,u)

(5)

针对非线性模型(5),应用GPOPS工具箱优化得到参考轨迹,记为(Xr,ur)。Xr与ur满足飞行器栖落动力学模型(5),即Xr=f(Xr,ur),其中Xr=[vr,μr,αr,qr,xr,hr]T为状态变量参考轨迹,ur=[Tr,δer]T为与状态变量参考轨迹Xr相对应的参考输入(在不引起混淆的情况下,本文将ur称为参考输入)。

将非线性模型(5)沿着参考轨迹(Xr,ur)进行泰勒展开,具体形式为

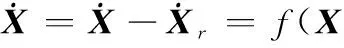
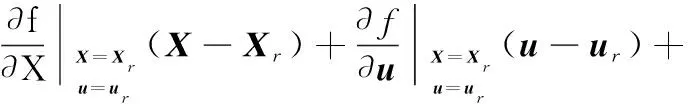
Ar(t)(X-Xr)+Br(t)(u-ur)+Ο=

Ar(t)ΔX+Br(t)Δu+Ο

(6)

为了得到Ar(t)与Br(t)的具体表达式,并且减轻计算量。定义[t0,tf]为整个栖落机动的时间范围,在整个栖落过程中均匀地取N个时刻点。在每个时刻点对应的参考轨迹上的参考点附近,对栖落系统的非线性模型(1)进行线性化。例如,在ti时刻所对应的参考轨迹中的参考点附近进行线性化,计算得到线性化模型为

(7)

那么在整个栖落机动的时间范围[t0,tf],栖落机动的线性时变模型为

(8)

(9)

则式(8)为栖落机动的分段线性化模型。

接下来设计切换系统跟踪参考轨迹的切换控制律。

2.2 切换控制律设计

直接设计切换系统控制律的工作复杂,可以从切换系统的子系统入手,设计每一个子系统的最优控制律,这种方法大大降低了工作难度。因此,可以借鉴线性时不变(linear time invariant,LTI)系统的最优控制律理论,对切换子系统设计轨迹跟踪切换控制律。令(tf-t0)/2N=Δt,在ti-Δt时刻,式(8)描述的切换系统切换到子系统为

(10)

针对式(10)描述的线性系统,需要寻找一个最优的控制uc,使得X能跟踪上Xr。为了实现控制目标,引入关于系统状态和控制参量的二次型性能指标，即

ΔuTRΔu+ΔXTQΔX)dt

(11)

设计控制律使J取极小值,其中R和Q是根据设计要求选定的权重矩阵,一般取对角常值矩阵。这是典型的线性二次型问题,设计系统的线性二次型调节器(linear quadratic regulator, LQR)。

为了计算满足条件的控制输入u*(t),引入哈密顿函数，即

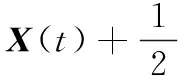
λ(t)TAiΔX(t)+λ(t)TBiΔu(t)

(12)

根据驻值条件

(13)

得

(14)

由正则方程得

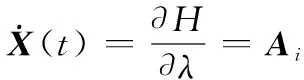
(15)

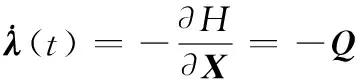
(16)

令协态方程(16)的解为

λ(t)=SiΔX(t), ∀t∈[t0,tf]

(17)

式中,Si待定。结合式(14)～式(17),得Si应满足矩阵方程,即黎卡提方程

(18)

设计最优控制输入为

u*(t)=kiΔX(t)

(19)

其中控制增益为

ki=-R-1BiSi

(20)

以上设计了切换系统中每一个子系统的最优控制律,在此控制器作用下,每一个子系统稳定并且状态量能收敛至参考点。然而,每一个子系统的稳定并不能保证整个切换系统的稳定,因此需要分析整个切换系统的稳定性。

切换系统的稳定性不仅取决于子系统的稳定性,还与切换规则息息相关。根据栖落机动的分段线性化过程可知其切换规则是受约束的,因此本节分析受约束作用下切换系统的稳定性。

对受约束作用下切换系统稳定性分析的方法主要包括:分段连续二次Lyapunov函数法(piecewise quadratic lyapunov function,PQLF)[18-19],类Lyapunov函数法[20],多重Lyapunov函数法(multiple lyapunov functions,MLFs)[21-22]。本文参考类Lyapunov函数法分析切换系统的稳定性。

对于线性切换系统的N个子系统,如果能找到每一个线性子系统对应的Lyapnov函数,并且满足切换前时刻的Lyapunov函数值不小于切换后时刻的Lyapunov函数值这一条件,那么对应的线性切换系统全局稳定。因此,如果能找到式(10)描述的线性切换子系统的Lyapunov函数Vi(ΔX)=ΔXTPiΔX,满足

(Ai+Biki)TPi+Pi(Ai+Biki)≤-Qi

(21)

Pi-1≥Pi

(22)

式中,Pi和Qi是正定对称矩阵。那么满足式(21)、式(22)的控制律ki(由式(20)得到)就是能保证切换系统稳定的子系统切换控制律。

在计算ki时,先根据式(20)确定ki,再由式(21)与式(22)核算此ki是否满足切换系统的稳定性要求。如果不满足,则调整式(18)中的权值Q与R,再次核算在此权值计算出的最优控制律ki是否满足式(21)与式(22)。直到找到满足式(21)、式(22)与式(20)的控制律ki。

同理,可分别计算出整个时间历程N个切换子系统的控制律ki。则整个时间历程的切换控制律的形式为

(23)

3 栖落轨迹跟踪控制律的吸引域计算

系统的吸引域即为系统的局部渐近稳定区域。第2节设计了栖落轨迹跟踪控制器。此控制器是根据分段线性近似模型设计得到的,因此该控制器只能保证分段线性系统(8)全局稳定,而在此控制作用下的闭环非线性栖落系统是局部稳定的,因此分析系统的吸引域是重要问题。本小节运用SOS最优化方法[23-24]计算该闭环非线性栖落系统的吸引域Ω。即计算参考轨迹附近的特定区域Ω,当系统的状态量X∈Ω时,则在所设计的轨迹跟踪控制器作用下,飞行器最终能栖落在目标落点区域Ωf里。下面在第3.1节介绍切换控制的轨迹吸引域的计算方法;为了降低SOSTOOLS[25-26]计算轨迹吸引域的难度,提高准确度,第3.2节提出了计算栖落轨迹吸引域的一种降保守性的方法;第3.3节引入了基于质点模型计算吸引域的方法。

3.1 栖落轨迹吸引域算法

为了描述沿着参考轨迹的吸引域,我们定义时变区域为

(24)

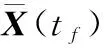
(25)

式中,Ωf表示栖落终点的目标范围。则此时的Ω(ρ,t)即为所求吸引域。

Ωf的具体定义为

(26)

式中,ρf是根据栖落终点的容许误差范围人为设定的。

为了保证条件(25)成立,需要满足

(27)

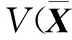
,ti)≤ρ(ti)

(28)

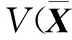
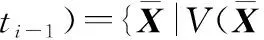
同样,如果系统在整个栖落时间[t0,tf]都满足上述条件,那么式(24)表示的Ω(ρ,t)就是栖落系统在参考轨迹附近的吸引域,吸引域计算过程整理成为

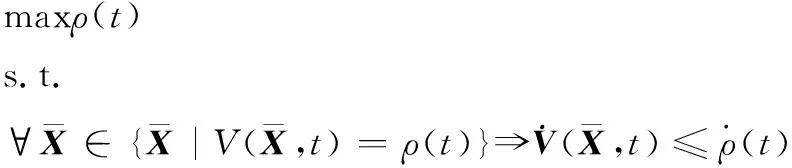
(29)

为了将非线性系统(1)的轨迹吸引域求解条件转化为SOS形式,先将式(29)表示的条件转化为

(30)

进而,条件(30)等价于

(31)

为了将条件(31)转化为SOS最优化问题,给出引理1。

引理1[27-28]给定多项式集{f1,…,fs},{g1,…,gt},{h1,…,hu}∈Rn,下面的两个条件是等价的:

(2) 存在多项式f∈p{f1,…,fs},g∈M{g1,…,gt},h∈I{h1,…,hu}满足f+g2+h=0,其中,Rn表示所有实数域上n元多项式的集合。

再根据引理1,条件(31)可转化为

(32)

式中,s1,s3∈Σ，Σ表示平方和多项式。取s3=1,将条件(32)简化,得到SOS最优化算法为

(33)

由于并不是所有的非负多项式都能用平方和的形式表示,因此算法(33)是算法(32)的充分条件。

因为SOS最优化方法适用于多项式系统,所以我们需要对式(1)中的f(X)进行泰勒展开,用泰勒展开的多项式系统去估计原非线性系统。

考虑算法(33)中的表达式为

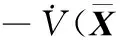
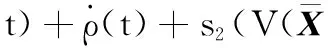
(34)

式中,s2的系数是变量;ρ(t)是与t相关的变量。而SOS最优化方法要求约束条件中的未知量之间是线性关系,所以将算法(33)转化为

(35)

为了简化问题,在计算吸引域时,以时间取样,将整个栖落时间[t0,tf]分为N段,比如计算时间范围内[tf-1-Δt,tf-1+Δt]的吸引域,将[tf-1-Δt,tf-1+Δt]范围内的ρf-1(t)用线性形式估计。因为ρf是由栖落终点的容许误差范围而人为设定的,所以ρf已知。设在[tf-1+Δt,tf]这一段时间内,吸引半径不变等于ρf,那么只需要计算tf-1这一时刻的ρf-1,就可以计算出ρf-1(t)。按照上述方法,以t=ti时刻取样,算法式(35)可简化为

(36)

其中

(37)

3.2 切换控制吸引域计算的降保守性方法

∀i∈[0,N](Ai+Biki)TSx+Sx(Ai+Biki)<0

(38)

为了解决由于Ω(ρ,ts)跳变带来的吸引域计算失真的问题,需要保证式(39)成立。

(39)

此时解出的在ts这一时刻前后的吸引域才是符合要求的[29]。

(40)

最后,ρi(t)以分段线性形式估计表达为

, ∀t∈[ti-Δt,ti+Δt)

(41)

ρi(t)即为系统在[ti-Δt,ti+Δt)这一时间段的吸引半径。进而得到整个栖落时间范围的分段线性表达式ρ(t)。

3.3 基于质点模型的栖落轨迹吸引域计算

(42)

式中,av表示加速度;ωμ表示航迹角速度。

简化后的质点模型输入是加速度av与航迹角速度ωμ。为了使这两个控制量符合实际六维系统的物理规律,需要添加输入饱和约束。将此约束加入到SOS算法式(36)中,约束具体表达式为

(43)

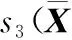
4 仿真结果与分析

4.1 栖落机动轨迹跟踪控制仿真

仿真中固定翼飞行器的质量与转动惯量分别为:m=0.8 kg,Iy=0.1 kg·m2。飞行器的其他物理参数见文献[8]。仿真中采用的飞行器动力学模型为式(1)所表示的栖落机动非线性模型,其中,气动参数由式(2)、式(3)和式(4)计算获得。在设计控制律时,将整个栖落时间区域[0,2 s]均匀分为20段,在{0 s,0.1 s,0.2 s,0.3 s,…,1.9 s,2 s}这21个时刻的参考点处分别得到线性化模型以便于控制律设计。在计算最优控制律时,设定式(11)中的权重矩阵为Q=diag[1.5,8,1.5,1.5,20,15],R=diag[1,50];进而联立式(20)～式(22)求解获得控制律。将所设计的控制律应用于栖落运动非线性动力学模型(1)进行仿真。

飞行器栖落机动理想初始飞行状态X*(t0)=[9.973 6,0,0.245 5,0,0,0],为了检验设计的控制律的状态量跟踪效果,设计实际的初始飞行速度具有偏差1 m/s,航迹角偏差为0.1 rad,迎角偏差为0.05 rad,俯仰角速度偏差为0.1 rad/s,高度与水平位置偏差都为1 m。仿真结果如图1～图3所示。其中,图1对应状态变量跟踪曲线,图2对应控制输入曲线,图3对应飞行器位置跟踪曲线。图1中蓝色虚线对应参考轨迹,红色实线对应切换控制响应曲线。可见,在切换控制器作用下,速度、航迹角、迎角、俯仰角速度、水平位置和高度均能跟踪参考曲线,并在终点时刻收敛到满足要求(|Δv|<0.5 m,|Δμ|<0.35 rad,|Δα|<0.35 rad,|Δx|<0.1 m,|Δh|<0.1 m)的范围内。验证了基于LQR与切换控制综合设计的控制器的有效性。

控制输入曲线如图2所示,图2中蓝色虚线表示参考输入曲线,红色实线表示切换闭环控制输入。可见,推力与升降舵偏转量虽然没有收敛到标称值,但是与理想输入值偏差范围合理。

图3描述了飞行器栖落机动位置跟踪曲线。其中蓝色虚线对应参考轨迹,绿色点划线对应开环响应曲线,红色实线对应切换控制闭环响应曲线。在栖落机动飞行结束时刻,参考栖落位置为(14.05,2.103),未加控制器的栖落位置为(13.6,2.518),切换控制下的栖落位置为(14.01,2.035)。

由此可见,在切换控制作用下,尽管初始位置偏差很大,但响应曲线最终能收敛到指定位置附近,符合栖落位置精度要求。而未加控制器的栖落位置与指定位置偏差较大,不符合栖落要求。验证了设计轨迹跟踪控制器的必要性与基于LQR与切换控制综合设计的轨迹跟踪控制器的有效性。

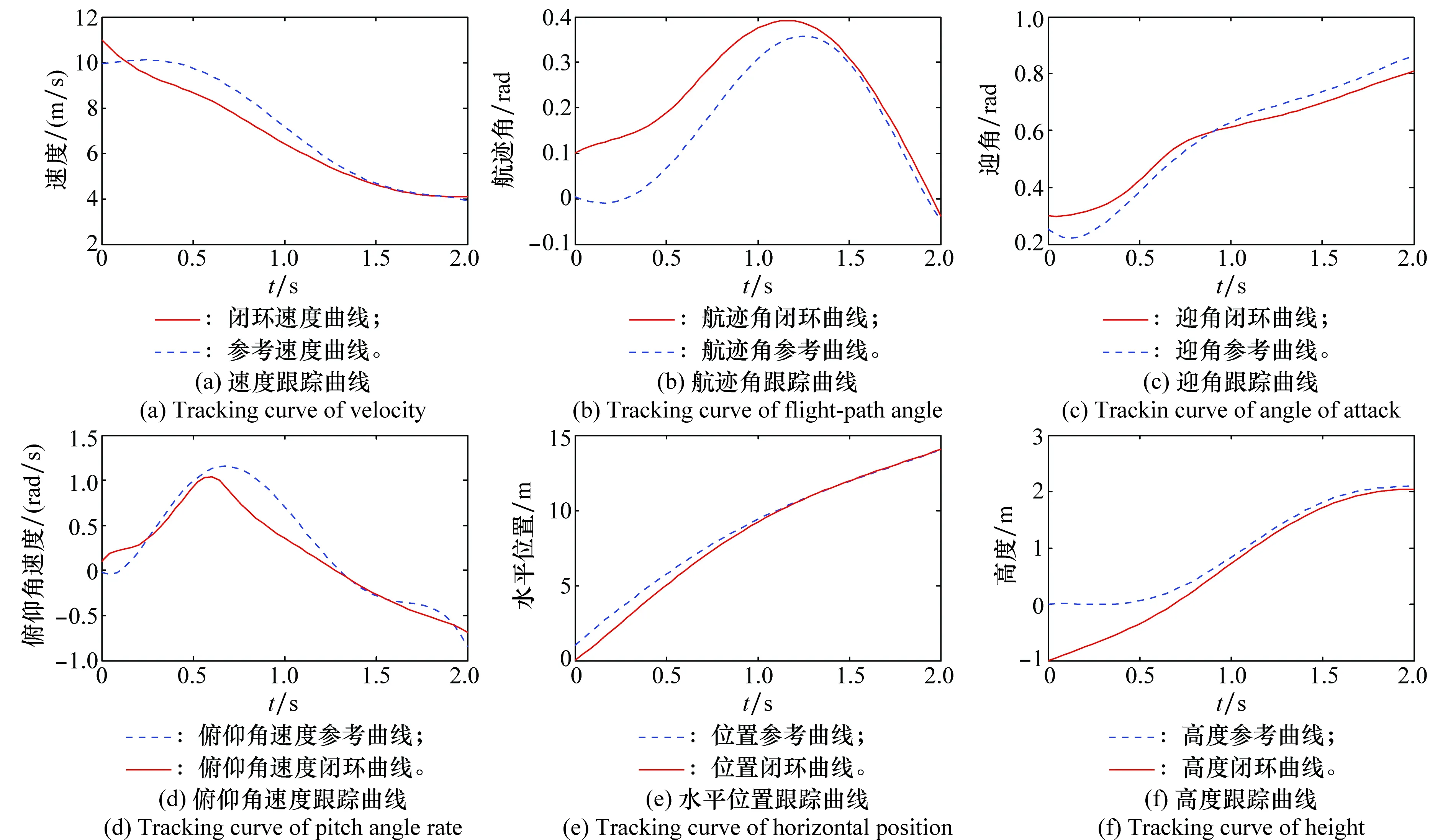
图1 状态变量跟踪曲线Fig.1 Tracking curve of state variables

图2 控制输入曲线Fig.2 Tracking curve of control input

图3 位置跟踪曲线Fig.3 Tracking curve of position

4.2 栖落机动轨迹吸引域仿真

，z=[ΔxΔhΔvΔμ]T

(44)

式中,U是4×4的实对称矩阵,由10个决定变量构成[30]。

接着将控制输入的约束条件(43)加入到SOS算法(36)中。根据六维模型仿真结果,对整个栖落机动过程的质点模型输入量进行了分段约束,具体约束范围如表1所示。

表1 栖落机动过程控制输入约束范围

Table 1 Scope of constraint of control input in perching process

在整个栖落时间[0,2 s]每隔0.1 s取一个时刻点,共取21个时刻点,联立式(43)与式(36)分别算出21个时刻点的吸引域,注意计算是从终点时刻的收敛半径计算开始的。对2 s这一终点时刻,期望终点误差0≤Δv≤0.5 m/s,|Δμ|≤0.35 rad,|Δx|≤0.1 m和|Δh|≤0.1 m。根据期望误差范围,并结合式(26),设置ρf为0.15。定下ρf之后,联立式(36)、式(37)与约束条件(43)算出1.9 s这一时刻的收敛半径ρf-1,同理递推计算出整个栖落过程的收敛半径。最后根据式(41)写出分段线性吸引半径,为了形象直观地表示吸引域,将其投影在xh平面,结果如图4所示,其中绿色椭圆表示吸引域。

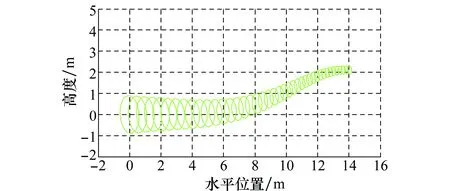
图4 吸引域在xh平面的投影Fig.4 Projection of the domain of attraction in xh plane

图4描述了分段线性吸引域在xh平面上的投影。每个椭圆代表对应时刻的吸引域,在轨迹跟踪控制器的作用下,前一个时刻椭圆内的所有状态量都会收敛到下一个时刻对应的椭圆吸引域内,进而可以推知,只要初始状态在0 s对应的椭圆吸引域内,最终位置都会收敛到设置的目标栖落域Ωf内。

图5描述了质点模型采样栖落轨迹与吸引域在xh平面的关系。仿真时,选取了5个在0 s对应的椭圆吸引域内不同的初始状态,仿真结果显示,栖落轨迹全都在所求吸引域内,且终点位置都收敛到所设的目标栖落域Ωf内,验证了对质点模型计算出的吸引域的有效性。

图5 质点模型栖落轨迹与吸引域在xh平面的投影Fig.5 Perching trajectory of particle model and the projection of thedomain of attraction in xh plane

图6描述了原六维非线性栖落机动模型栖落轨迹与吸引域在xh平面的关系。仿真时根据第2.2节相关内容设置切换控制器,使原六维模型的状态变量(x,h,v,μ)快速跟踪质点模型的状态变量(xr,hr,vr,μr)。已知质点模型的栖落机动仿真曲线在吸引域内,则原六维非线性模型栖落机动仿真曲线也应在吸引域内。仿真结果显示,原六维非线性模型的栖落轨迹全都在所求吸引域内,且终点位置都收敛到所设的目标栖落域Ωf内。

图6 六维非线性模型栖落轨迹与吸引域在xh平面的投影Fig.6 Perching trajectory of 6-d nonlinear model and the projection of domain of attraction in xh plane

5 结 论

本文采用基于切换控制与最优控制相结合的综合控制算法,设计飞行器栖落机动轨迹跟踪控制律。然后,运用SOS最优化算法,计算了栖落轨迹吸引域。针对切换系统的特性,研究了降低吸引域计算保守性的方法。最后对飞行器栖落机动过程进行了仿真验证。仿真结果表明,基于切换控制与最优控制设计的控制器使得飞行器可以跟踪上参考轨迹,验证了所设计的轨迹跟踪控制器的有效性。仿真结果还表明,基于SOS算法沿着参考轨迹计算的吸引域Ω,当X∈Ω时,飞行器能栖落在目标范围内,验证了所计算的轨迹吸引域的正确性。