基于步进加速退化建模的剩余寿命在线预测
2018-11-09蔡忠义郭建胜陈云翔董骁雄项华春
蔡忠义, 郭建胜, 陈云翔, 董骁雄, 项华春
(空军工程大学装备管理与无人机工程学院, 陕西 西安 710051)
0 引 言
随着状态监测技术的发展,以设备退化状态监控信息为依据,及时准确预测设备的剩余寿命是制定设备最优维护方案、备件订购策略和健康管理的重要依据[1]。剩余寿命预测主要是求解各监测时刻上目标产品的剩余寿命分布函数。基于Wiener过程的剩余寿命预测分为两个环节:
一是进行退化建模,利用同类产品的退化信息,求解出反映总体退化特征的固定系数估计值和反映个体退化特征的随机系数先验值。由于产品退化过程中受随机不确性、测量不确定性等因素的影响,在退化建模时需要考虑以下退化特征:
(1)非线性特征。对具有非线性特征的退化数据处理,一般可采用两种方法进行处理。一是对非线性数据进行线性化处理。Whtimore[2]首次提出时间尺度模型,将非线性退化数据转化为线性退化数据,给出产品概率密度函数(probability density function,PDF)表达式。由于计算过程简单,使得该方法得以广泛应用[3]。二是直接建立非线性Wiener退化过程建模,给出退化产品寿命的PDF近似表达式。文献[4-5]提出了非线性Wiener退化过程建模,给出了相应的PDF近似表达式。相关的模型误设研究[6],表明后者进行建模评估的精度要高于前者,但后者建模和计算过程较为复杂。
(2)随机效应。随机效应是指同类产品中个体差异在退化过程中的具体表现。将描述随机效应的随机变量称为随机系数。一般做法是将Wiener过程参数进行随机化处理。文献[7]将漂移系数和扩散系数都看作是随机变量并作为先验分布,通过贝叶斯推断,得到随机系数的后验均值,但由于涉及复杂推导,并未给出含有双随机系数的PDF表达式。文献[8-9]认为同类产品中个体差异主要受Wiener过程中漂移系数的影响,只将漂移系数看作为正态分布随机变量。这种做法能较好地处理总体退化特征与个体退化差异之间的关系,所建的模型具有良好的模型拟合性。
(3)测量误差。由于测量过程中受噪声、扰动、不稳定测量设备的影响,测量数据中含有一定误差。一般做法是将测量误差看作为均值为零的正态随机变量且与实际退化过程之间相互独立[10]。文献[11-12]建立了同时考虑随机效应和测量误差的线性Wiener退化模型,给出了相应的PDF近似表达式。文献[13]综合分析了带非线性特征、随机效应和测量误差的模型误设问题,指出模型中考虑测量误差可以有效提高评估精度。
二是进行剩余寿命预测建模。剩余寿命建模实际上给出目标产品剩余寿命的PDF。文献[14]给出了含有测量误差的线性Wiener过程的目标产品剩余寿命的PDF近似表达式。对于带测量误差的剩余寿命预测的关键是对剩余寿命PDF中随机系数或当前实际退化状态进行实时更新,以体现目标产品的个性特征。一般有以下两种方法:
(1)随机系数的贝叶斯更新方法。文献[15]首次将贝叶斯推断方法用于剩余寿命分布模型中随机系数的更新,给出了先验信息与目标产品退化信息之间的更新公式。文献[13]应用贝叶斯推断方法,进一步推导出了考虑测量误差和随机效应的非线性Wiener过程的目标产品剩余寿命中随机系数的更新公式。这种方法充分利用了同类产品退化先验信息,使得目标产品剩余寿命预测结果能反映其个体退化特征,但由于目标产品实际退化状态未知,可能存在一定误差。
(2)随机系数和实际状态的联合更新方法。常用的更新方法有随机滤波模型[16]、隐马尔可夫模型[17]等。其中,随机滤波模型将随机系数、当前实际状态都作为隐含状态,建立了观测过程与随机系数、当前实际状态之间的状态空间模型,实现对隐含状态的估计和更新。这种方法具有较高的预测精度,但计算过程较为复杂。
因此,本文针对SSADT下具有非线性、随机效应、测量误差等特征的退化数据,建立加速退化模型,给出总体观测增量数据的轮廓对数似然函数,得到模型中固定系数估计值和随机系数先验值;建立与目标产品个体退化特征相匹配的剩余寿命PDF,引入随机系数更新贝叶斯方法,求出剩余寿命模型中随机系数后验值。
1 步进加速退化建模
1.1 模型假设
(1)受试产品的关键性能参数仅有一个,其退化过程X(t)可用Wiener过程进行描述
X(t)=λΛ(t;θ)+σBB(t)
(1)
式中,λ为漂移系数;σB为扩散系数;B(t)为标准布朗运动;Λ(t;θ)为时间t的连续非减函数(θ为未知参数向量),表征非线性特征。
(2)选择温度为加速应力、Arrhenius模型为加速模型。
(3)受试产品在各加速应力下发生的退化不可逆且退化机理不变,满足累积退化模型要求;
(4)受试产品的性能退化数据在观测中会产生测量误差(在寿命预测性能约束的可行域内),其观测过程Y(t)表示为
Y(t)=X(t)+ε=λΛ(t;θ)+σBB(t)+ε
(2)
式中,ε表示测量误差,一般认为ε~N(0,σ2)且与λ,σB相互独立。
1.2 步进加速退化模型
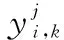
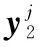
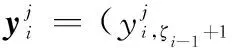
由SSADT过程可知,当前加速应力下产品观测初值是前一应力下观测末值。根据式(2),建立各加速应力下观测数据Y(t)的关系模型为
yi,k=
(3)
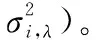
1.3 加速模型
一般认为Wiener过程的漂移系数与应力有关。采用Arrhenius模型来描述漂移系数与温度应力之间的关系,即
λi=aexp(-b/Si)
(4)
式中,a和b为待定参数;Si为第i个应力;λi为应力Si下产品的漂移系数。
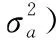
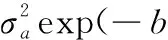
(5)
2 参数估计
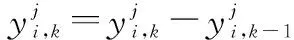
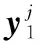
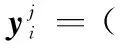
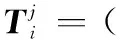
根据多元Wiener过程性质,观测增量数据向量Δyj服从n元正态分布[4]。
(1)当给定λi时,则有
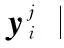
(6)

(7)
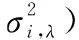
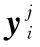
(8)
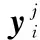

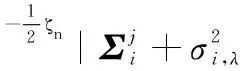

(9)
根据式(9),基于m个产品观测数据集Δy={Δy1,Δy2,…,Δym},建立未知参数集Θ的对数似然函数为

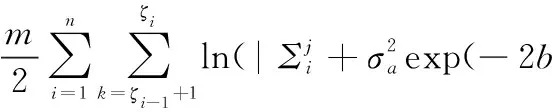
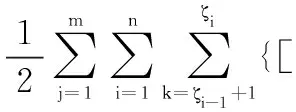
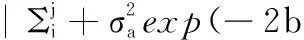
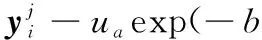
(10)
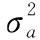
(11)

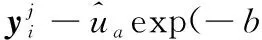
(12)
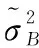
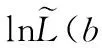


(13)

3 剩余寿命预测模型
3.1 剩余寿命分布函数

将目标产品在当前观测时刻ti,k处的剩余寿命Li,k定义为
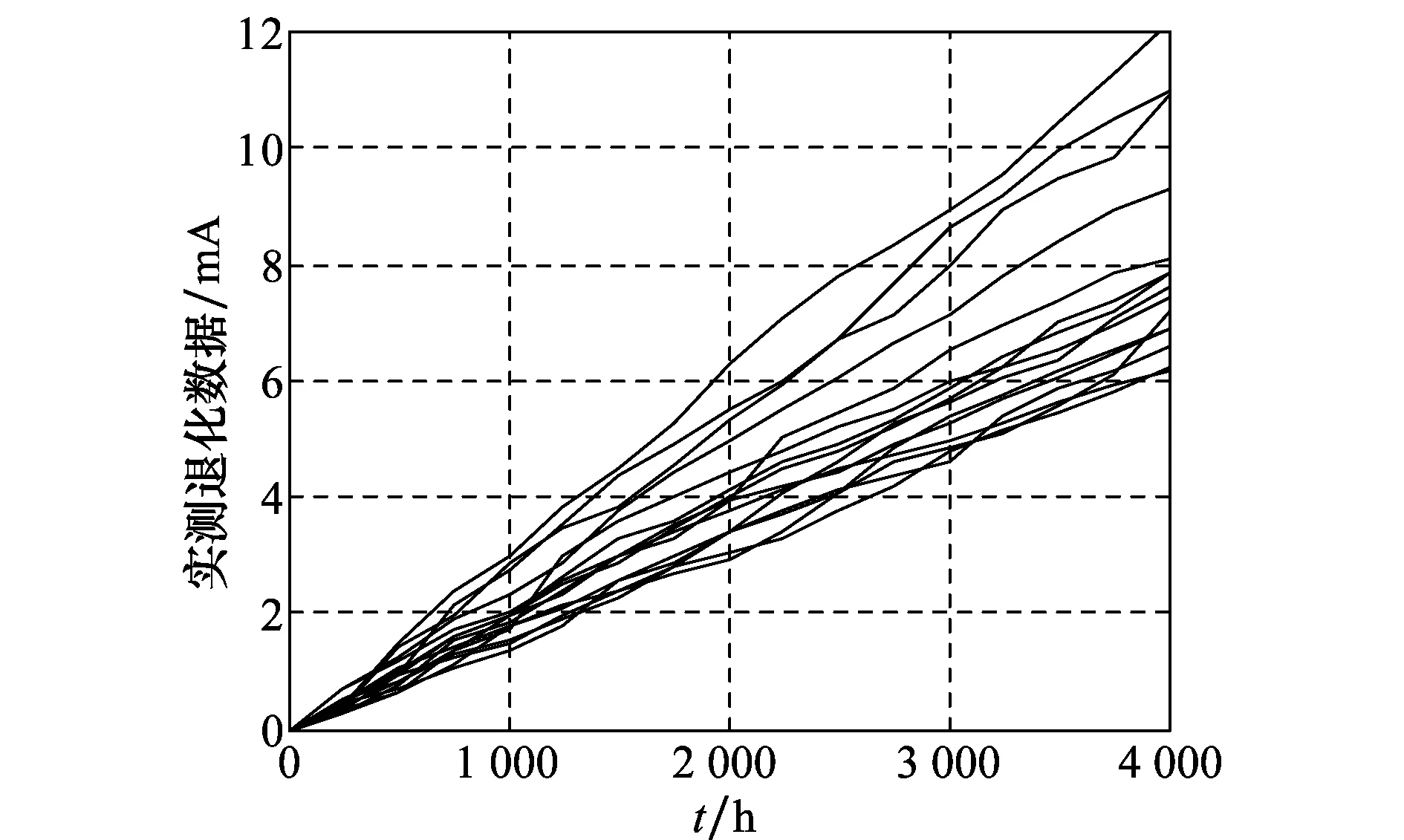
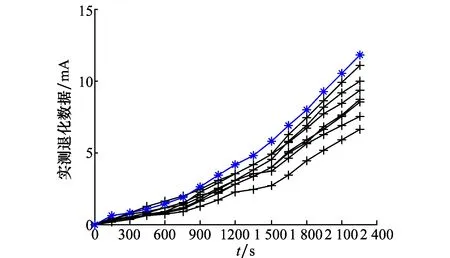
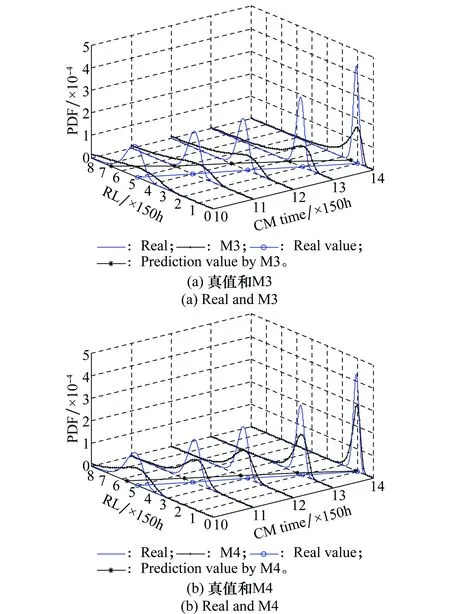
Li,k=inf{li,k:X(ti,k+li,k)≥w|X(ti,k) (14) (15) 式中 β(li,k)=(li,k+ti,k)c-(ti,k)c-c(li,k+ti,k)c-1li,k (16) φ(li,k)=(li,k+ti,k)c-(ti,k)c (17) ε,ε~N(0,σ2) (18) ≅ (19) 当前时刻ti,k处目标产品剩余寿命的期望为 (20) (21) 其中 (22) (23) (24) (25) 本文依据文献[18]给出的激光器实测退化数据,仿真得到激光器在步进加速应力下的退化数据,以验证所提出方法的正确性。文献[8,19]也是基于该激光器数据仿真得到的加速退化数据,研究加速退化建模问题。 已知该激光器的性能参数为工作电流(单位:mA),正常工作温度为25 ℃。激光器的工作电流会随着时间的延长而出现递增的退化现象。图1给出了15组激光器的实测退化数据。 图1 15组激光器的实测退化数据Fig.1 15 sets of lasers measured degradation data 已知该激光器受温度影响较为敏感,其性能退化速率与温度之间的关系符合Arrhenius模型。引用文献[8]中给出的激光器退化模型参数真值如表1所示。引入测量误差,设定σ=0.08。采用蒙特卡罗仿真方法,设定步进应力为25 ℃、50 ℃、75 ℃,每个应力下测量5次,测量间隔为150 h,得到8组仿真的步进应力下实际退化数据(不带测量误差,此时σ=0)和观测数据见图2、图3(图中蓝线为目标产品的退化轨迹)。 图2 仿真的SSADT实际退化数据Fig.2 Simulated SSADT actual degradation data 图3 仿真的SSADT观测数据Fig.3 Simulated SSADT observed data 利用仿真得到的激光器SSADT观测数据来验证本文所提出方法的正确性和优势。将文献[19]中未考虑测量误差的非线性加速退化建模方法记为M1;将带测量误差的线性加速退化建模方法(即c=1)记为M2;本文提出的带测量误差的非线性加速退化建模方法记为M3(由此可见,M1和M2是M3的特殊情况)。采用赤池信息准则(AIC)和均方误差(MSE)来判别各模型之间的拟合优劣性。 表1 不同模型的参数估计结果 以SSADT中第8个样本为目标产品,其在第2 250 h处的实际退化数值为11.81 mA。为了验证本文在剩余寿命中引入随机系数更新贝叶斯方法的有效性,假设该激光器的退化失效阈值为11.81 mA,在2 250 h处刚好失效。将M3的剩余寿命预测模型中加入随机系数在线更新方法记为M4。通过对比M3、M4与真实值剩余寿命预测结果来验证M4的优势。 表2 观测末期随机系数后验值 由表2可知,M4计算出的随机系数均值和方差的后验值介于其先验值与真实值之间;而M3计算出的随机系数均值和方差的后验值离真值较远。这是因为M4在M3的基础上引入随机系数更新方法,能更好地反映出目标产品的个体退化特征,具有更好的估计优势。 分别将M3、M4的随机系数后验值以及真值,代入式(19)和式(20),计算出目标产品的剩余寿命PDF如图4所示。 由图4可知,M4的剩余寿命PDF比M3的剩余寿命PDF更窄且更接近真值的PDF;同时M4的目标产品剩余寿命点估计值较M3更接近于真值的剩余寿命点估计值。这是因为M4的剩余寿命PDF采用随机系数更新方法,使得目标产品在剩余寿命预测过程中不断以自身观测数据来更新随机系数,使得预测结果更逼近于其真实退化过程。说明本文所提出的带测量误差的退化模型和基于随机系数贝叶斯更新的剩余寿命预测模型具有更好的预测精度。 图4 不同方法下剩余寿命的PDFFig.4 Remaining lifetime PDF by different methods (1)本文建立了带测量误差的非线性步进加速退化模型,给出了基于Fminsearch函数的轮廓似然函数求解方法,得到了固定系数估计值和随机系数先验值,为解决退化模型中多参数估计提供了可行途径; (2)引入随机系数贝叶斯更新方法,推导出了目标产品剩余寿命的PDF近似表达式,利用目标产品退化信息来更新剩余寿命的随机系数后验值,实现了目标产品剩余寿命预测结果在线更新; (3)结合仿真实例分析,与现有算法对比分析,验证了本文所建模型在估计误差和预测精度上具有一定优势。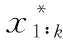



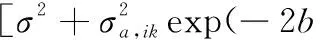
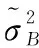
3.2 随机系数在线更新



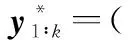


4 仿真实例

4.1 退化模型的参数估计
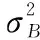

4.2 随机系数在线更新
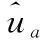

4.3 目标产品剩余寿命预测
5 结 论
