有限任务间隔时间内的装备选择性维修决策研究

王少华, 张仕新, 李 勇, 刘宏祥

(1. 陆军装甲兵学院装备保障与再制造系, 北京 100072; 2. 陆军装甲兵学院科研学术处, 北京 100072)

0 引 言

在军事装备保障领域,保持和恢复装备的战备完好性、确保装备在任务期间的可靠性是维修保障工作的最主要目标,但是受维修保障任务强度、任务间隔时间以及可用保障资源等诸多因素的影响,往往无法对装备实施“应修尽修”[1],特别是在相邻任务周期内,在给定维修时间的条件下,必须实施选择性维修,即对有限的维修工作进行组合,以满足相关约束,并尽量提高下次任务周期内的装备可靠度,为确保任务成功提供支撑[2-4]。

选择性维修决策主要包括维修对象的选择以及维修行为的选择,研究者已经对选择性维修进行了一定的研究。Bris[5]以系统可用度为约束,以费用最小化为目标,提出了复杂系统的选择性维修决策方法,Laggoune[6]和Wang[7]等采用与Bris同样的假设,采用不同的求解算法对选择性维修方法进行了研究。但上述模型假设系统各部件皆为随机失效并且只进行换件修理,不适于描述拥有劣化期的复杂系统。Moghaddam[8]等考虑了系统役龄,以维修费用为约束,以系统可靠性最大化为目标,研究了选择性维修决策方法,但该模型未考虑最小维修等情况。Cassady[9]等以威布尔模型描述部件可靠度,以维修时间为约束,以系统可靠度最大化为目标,考虑了最小维修和换件维修,建立了多部件系统的选择性维修决策模型。但并未提出有效的优化求解算法。为此,本文以最小维修和换件修理构成部件待选方案,为多部件系统在有间隔任务过程中的选择性维修决策建模和求解算法进行研究[10-11]。

1 多任务间隔的装备状态变化模型

对于装甲装备来说,其系统构成往往十分复杂,根据系统功能与任务之间的映射关系,可将装备简化为复杂的串并联系统。为了便于分析,将装备视为由子系统i(i=1,2,…,m)串联而成的复杂系统,子系统i由ni(i=1,2,…,m)个相同部件并联组成,将子系统i中第j个部件表示为Si,j,各部件、子系统、系统状态为正常或故障[12-13]。

根据军事装备运用规律,假设装备系统连续执行多个作战任务,各任务之间存在一定的时间间隔,在有限的任务间隔期内可以对系统内部件进行事后维修或预防性维修,以提高后续任务的可靠度[14]。假设系统内各部件具有唯一的故障模式,部件的维修行为包括:事后维修和预防性维修,其中故障后可采用最小维修或事后更换,预防性维修为预防性更换。从合理性上分析,预防性更换时间应低于最小维修时间,而最小维修时间应小于事后更换时间,最小维修的成本低于预防性更换,而预防性更换的成本应低于事后更换。

在作战任务之间,维修行为将改变各部件的状态,影响任务周期内的系统可靠性。这里以k(k=1,2,…)表示系统的任务周期数,分别以Xi,j(k)和Yi,j(k)表示部件Si,j在第k次任务开始前和结束后的状态,则

(1)

同样,分系统i的状态也标识为{0,1},其中,0表示故障,1表示正常,则

(2)

由多个分系统串联而成的整装可靠度为

(3)

当任务k完成后,装备系统以及其子系统的状态同样可采用相同方式进行计算，即

(4)

(5)

(6)

采用可靠度函数来表示装备系统内各部件的状态,假定系统内部件Si,j在任务k开始时处于正常工作状态,将部件Si,j在第k次任务期间未发生故障的概率表示为

rij(k)=P(Yij(k)=1|Yij(k)=1)

(7)

假设部件的可靠度函数已知,则ri,j表示为部件Si,j的条件可靠度,部件Si,j在任务k开始前、结束后役龄和任务周期长度分别表示为Pi,j(k)、Qi,j(k)和L(k),显然有Qi,j(k)=Pi,j(k)+L(k),即

rij(k)=R(Qij(k)|Pij(k))=

R(Pij(k)+L(k))/R(Pij(k))

(8)

假设系统内各子系统内部件的可靠度都符合威布尔分布模型,且同一子系统内部件可靠度函数相同,第i个子系统内部件的威布尔分布形状参数和尺度参数分别为βi和ηi,即

(9)

部件Si,j在任务k结束时处于可用状态的概率Ri,j(k)取决于任务周期内的条件可靠度rij(k)和任务初始状态Xi,j(k),即

Rij(k)=P(Yij(k)=1)=rij(k)Xij(k)

(10)

则装备系统在任务k结束后的可靠度可表示为

(11)

2 多任务间隔的装备维修行为

作为序贯执行多项任务的军事装备,在有限的任务间隔期内通过选择性维修最大限度地提高装备的任务可靠度是维修决策的关键。当某次任务结束后,系统内部件Si,j(i=1,2,…,m;j=1,2,…,ni)可能处于正常或故障状态,对于故障部件,维修行为集合为{最小维修,事后更换};对于正常部件,维修行为集合为{不维修,预防性更换}。假定第k次任务已经结束,针对部件状态进行相应的维修,不同的维修行为对部件状态和役龄产生的影响如表1所示。

表1 维修行为及其效果

由表1可知,不维修和最小维修在执行前后并不改变部件的可靠性,只是通过维修达到排除故障的目的,部件在下个任务周期内不发生故障的概率并未发生改变;事后更换和预防性更换则能够通过换件将部件役龄归零,对于威布尔分布形状参数βi>1的部件,更换能够提高部件在任务周期内的可靠度。

对于给定的子系统i,其中部件Si,j(j=1,…,ni)的维修时间是相同的,将最小维修时间表示为tmi,事后更换时间表示为tfri,预防性更换时间表示为tpri,由于事后更换易造成较大的保障延迟,因此通常tri的值最大,为了简化模型,这里假定上述3个参数取值皆为常数。

这里以Wi,j(k)表示任务k结束后部件Si,j的最小维修决策变量,即

(12)

则在任务k结束后装备进行最小维修的总时间可以表示为

(13)

同样,可以得到任务k结束后部件Si,j的更换决策变量为

(14)

在任务k结束后装备进行部件更换的总时间TR(k)可以分为事后更换时间TFR(k)和TPR(k),TFR(k)的计算式为:

(15)

TPR(k)的计算式为

(16)

则在一个任务间隔期内,对装备进行维修的总时间为

T(k)=TM(k)+TFR(k)+TPR(k)

(17)

3 多任务间隔的装备选择性维修决策

3.1 选择性维修决策模型

在执行多任务的间隔期内,可在任务间隔期约束条件下结合部件状态进行相应的选择性维修决策,以最大限度地提高系统在下一任务周期保持正常状态的概率。由于装备在多任务间隔期内进行维修决策,因此维修决策是序贯决策问题,假定在任务k结束后系统内部件Si,j(i=1,2,…,m;j=1,2,…,ni)的状态已知,则系统维修决策问题即为Wi,j(k)和Vi,j(k)(i=1,2,…,m;j=1,2,…,ni)的赋值问题,决策目标是使第k任务周期内装备可靠度最大化,决策问题可视为0-1非线性优化问题,则

maxR(k+1)=

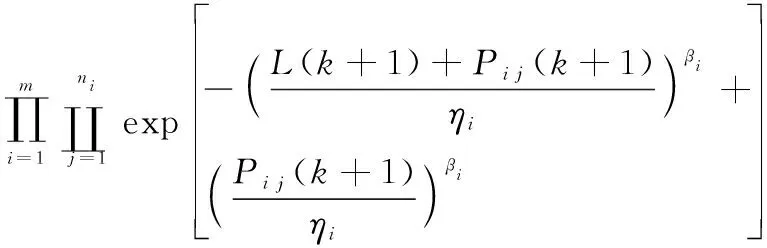
(18)

s.t.

T(k)≤MaxT

(19)

Wij(k)+Vij(k)≤1;∀i,j

(20)

Yij(k)+Wij(k)≤1;∀i,j

(21)

Xij(k+1)=Yij(k)+Wij(k)+

Vij(k)(1-Yij(k));∀i,j

(22)

Pij(k+1)=(Pij(k)+L(k))(1-Vij(k));∀i,j

(23)

式中,MaxT为相邻任务之间的时间间隔,即维修周期长度;式(20)能够保证一次维修中被修部件不同时进行最小维修和更换;式(21)保证正常工作部件不进行最小维修;式(22)用来更新下一任务开始时系统各部件的状态,若维修或更换则置部件状态为0,若无维修则保持修前状态;式(23)用来更新下一任务开始时部件役龄,若不更换,则延续第k次任务结束时的役龄,若更换,则役龄置0。

3.2 选择性维修决策优化

对于第2.1节确定的决策模型,当部件数量较少时,可以采用枚举法等进行优化求解[15],但随着部件数量的增加,决策解空间将随之成指数递增。为了提高求解效率,这里采用遗传算法进行维修决策优化,采用遗传算法工具箱GAOT进行优化求解,具体步骤为:

步骤1构造染色体,由Wi,j(k)和Vi,j(k)的定义可知,直接采用二进制编码,每部件占用两个二进制位,因此每个染色体长度为2 m;

步骤2确定种群规模、最大迭代次数、初始交叉率、变异率等参数;

步骤3计算各染色体的适应度。按照式(18)计算各染色体对应的装备任务可靠度R,适应度函数f取值越低,被选中概率越大,因此令f=-R,由于约束条件的存在,可能出现不可行解,将此类染色体f置0,以降低其遗传概率;

步骤4遗传操作。(a)选择操作:将随机遍历抽样与基于适应度重插法相结合,以保持种群的多样性,防止算法过早收敛,使最优个体获得更高的繁殖概率;(b)交叉操作:采用基于交叉算子的重组策略,采用多点交叉算子,以提高算法对解空间的搜索效率;(c)变异操作:为了增加种群的多样性,采用时变的变异概率,即在迭代前期取较大值的变异率,以扩大搜索范围,随迭代次数的累加逐渐缩小变异概率,以加快收敛速度。

步骤5终止条件。当迭代次数满足终止条件,输出最优解。

通过上述遗传迭代计算,即可得到当前选择性维修的最优解。max(-f)的值越大表明参数估计效果越好,因此可利用该指标检验上述参数估计方法的有效性。

4 案例分析

假设某型抢修装备分别配备有两套发电机和电焊机,发电机为电焊设备提供能源,在战时保障时要求至少有1套发电机和电焊设备正常工作。该型装备可视为两个并联系统串联而成的系统,将发电机标识为S11和S12,将电焊机标识为S21和S22。假设发电机和电焊机的可靠度服从威布尔分布,设备的可靠度参数与维修时间参数如表2所示。

表2 可靠度参数与维修时间参数/h

假设在任务k完成后,该系统以及内各部件状态和役龄如表3所示。

表3 系统内各部件状态和役龄(任务k完成后)

如表3所示,系统中S12和S21发生损坏,S11和S22正常工作,系统也能正常工作。假设下一任务在8 h后开始,即MaxT=8,下一任务周期长度L(k)=50,决策者需要在下次任务开始前进行选择性维修,以提高装备在任务周期内的可靠性。由第2节中求解模型可知系统中4个部件各有2个决策变量,有28=256个理论解,采用本文提出的基于遗传算法的求解方法进行优化决策。

设置种群规模NIND=30,最大迭代次数MaxGen=50,代际保留比率GGap=0.95,交叉几率px=0.7,变异概率pm=0.02;运行Matlab求解程序,可得到最优决策解为W=[0,1,1,0],V=[1,0,0,1],即S12和S21实施最小维修,S11和S22实施换件维修,由约束条件可知,S11和S22实施的换件维修为预防性更换,修后下次任务可靠度R=0.808 3。

迭代求解过程如图1所示。由图1可知,选择维修决策的遗传算法求解过程呈现较强的一致性,最优解和求解均值都能够快速收敛,表明求解结果是可信的。采用枚举法检验遗传算法求解结果的有效性,在256个理论

解中按照式(18)～式(22)求得所有的决策可行解,如表4所示。

图1 遗传算法迭代求解过程Fig.1 Iterative calculation process of genetic algorithm

可行解W11W12W21W22V11V12V21V22R(k+1)T(k)/h1011010010.808 382010000110.800 483010010100.798 374011000010.752 665010000100.743 356000001010.707 587010010010.703 968001010010.683 479001001000.679 3710011010000.675 9511000010100.675 0612010000010.655 4413011000000.629 3314000010010.595 1515000000110.581 6716001010000.571 5417001000010.546 9518000000100.540 2419000000010.476 3320001000000.457 3221000011000.446 1722000001000.429 1523010010000.426 9324010000000.397 5125000010000.361 0226000000000.288 90

由表4中的数据可知,由遗传算法得到的即为可行解中最优解,本次维修耗费8 h,满足约束条件。完成修理后,系统状态为X(k+1)=[0,1,1,0],役龄为P(k+1)=[0,1,1,0],开始执行第k+1次任务,系统状态发生随机变化,并在任务周期后依据系统该状态进行序贯的维修决策。假设在第k+1次任务后执行30次任务,任务周期长度L和任务间隔期MaxT保持不变,分别为50 h和8 h,通过多次仿真,得到了在任务周期之间序贯维修条件下装备任务可靠度的变化曲线,如图2所示。

图2 装备任务可靠度变化曲线Fig.2 Reliability curve of equipment task

由图2可知,在装备系统随机劣化和选择性维修条件下,装备系统的任务可靠度能够保持在0.75～0.85,任务可靠度相对稳定。如果系统可靠度不满足需求,可通过增加装备数量或增加任务间隔期的方式提高系统可靠度。以任务间隔期为例,间隔期越长,可选的维修策略越多,从而提高装备系统的任务可靠度,分别置MaxT为5 h、6 h、7 h,通过仿真计算装备的任务可靠度,结果如图3所示。

图3 不同MaxT下装备的任务可靠度变化曲线Fig.3 Reliability curve of different MaxT equipment mission

对比图3中不同MaxT条件下装备任务可靠度的变化曲线,可知随着MaxT的降低,系统任务可靠度也呈下降的趋势。当MaxT降低时,当系统内部件发生故障时,执行耗时较大的事后更换和预防性更换的机会被限制了,降低了序贯任务开始时系统的可靠度,以第k次任务为例,当MaxT=8时,可对S12和S21实施最小维修,S11和S22实施预防性更换,修后役龄为[0,60,40,0],当MaxT=4时,则只能对S12实施最小维修,S22实施预防性更换,修后役龄为[50,60,40,0],导致任务可靠度降低。因此从决策角度看,可通过调整任务间隔期的长度来确保任务可靠度达到可接受的程度。从图3的仿真分析结果也可以看出,本文提出的选择性维修优化求解算法是有效的。

5 结 论

由于军事复杂装备系统等对任务可靠性偏好程度较高,为了在序贯任务过程中，在有限维修时间约束条件下,提高装备的任务可靠度,本文建立了复杂串并联系统任务可靠度模型,以最小维修、预防更换和事后更换为维修策略,建立了以总维修时间为约束,以任务可靠度最大为目标的选择性维修决策模型。采用遗传算法建立了选择性维修决策优化求解算法,解决了求解空间爆炸问题。案例分析表明,本文建立的有限任务间隔时间内装备选择性维修决策模型是有效的。由于选择性维修决策往往面临着备件、工具等时间之外的约束条件,下一步有必要针对这一问题展开进一步的研究。