基于深度学习和集成学习的辐射源信号识别

黄颖坤, 金炜东, 余志斌, 吴昀璞

(西南交通大学电气工程学院, 四川 成都 610031)

0 引 言

雷达辐射源信号(radar emitter signal,RES)识别是雷达对抗信息处理的重要内容,它是在分选的基础上,提取信号中雷达的工作参数和特征参数,然后利用这些参数获取该雷达目标的体制、用途和型号、载体平台等信息,进而对战场态势、威胁等级、活动规律、战术意图等进行推理,为己方决策提供重要情报支持[1]。作为一个典型的模式识别过程,RES识别的性能依赖于有效的分类特征。然而,面对当前广泛应用的新型复杂体制雷达,基于常规五参数的RES识别方式已难以胜任现代战场复杂的电磁环境。为弥补五参数对RES识别能力的不足,国内外学者从时域[2-4]、频域[5-7]、时频域[8-14]等多角度进行分析,研究提出了多种新的RES特征,并取得了较好的识别效果。但是,截获的雷达信号分布往往是未知的,而有效特征组合的选择通常要依赖于专家的经验,识别的准确率难以保证。因此,寻求一种基于数据的自主特征学习方法对提升RES识别性能具有重要的意义。随着近几年人工智能技术的快速发展,雷达对抗信号处理朝智能化发展已成共识。其中,深度学习及其应用是人工智能领域的一个研究热点。

当前,深度学习已经在一些模式识别领域得到了很好的效果[15-19],诸如语音识别、图像分类、自然语言处理等。同时,国内外学者致力于将深度学习引入到RES识别上来[20-24]。如文献[21]实现栈式编码器(stacked auto encoder, SAE)对RES时频图像的特征提取,并通过仿真实验验证方法的有效性;文献[22]提出了基于深度信念网络(deep belief network, DBN)限制玻尔兹曼机的RES识别;文献[23-24]首先对RES进行时频分析,提取信号的时频特征作为卷积神经网络(convolutional neural network,CNN)的输入,训练CNN进行RES识别。SAE、DBN和CNN都是一种较为常见的深度神经网络(deep neural networks,DNN)模型,它能对底层特征进行非线性组合,形成更为抽象、有效的特征。因此,本文采用文献[25]提出的栈式降噪自编码(stacked denoising autoencoders,SDAE)模型来学习RES的特征。同时,考虑到利用集成学习的思想能构建一个有效的组合分类器模型,可以用来替代大多数深度学习应用中采用的Softmax分类器。基于此,本文提出了一种结合深度学习和集成学习的RES识别方法,该模型的具体流程如图1所示。首先,在预处理阶段对信号进行去噪。由于瞬时频率携带着大量表征RES调制特征的有效信息,且抗干扰性强。因此,利用Morlet小波变换来获得RES的时频图像。然后,创建一个含有多个隐含层的DNN模型提取时频图像的深度特征。最后,在分类器设计阶段,构造一个多SVM线性组合分类器(multi-SVM linear Combination Classifier,MSVMLC)进行分类识别。

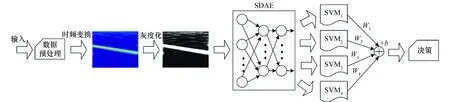
图1 基于深度学习和集成学习的RES识别流程图Fig.1 Flow chart of RES recognition based on deep learning and ensemble learning

1 降噪自编码

自编码器(autoencoder,AE)通过编码和解码两个过程实现对输入的复现,这个过程是一个自主特征学习的过程。自编码器可以看成是含有一个3层的神经网络,包括一个输入层、隐含层和输出层。隐含层的输出就是编码器学习到的特征,是输入不同层面的描述。AE的学习过程如图2所示。

图2 AE模型Fig.2 Model of AE

隐含层和输出层通常选用Sigmoid作为激活函数,通过梯度下降法最小化输入和输出的损失函数,一般选择交叉熵作为其损失函数WE:

该训练过程没有用到输入的标签,是一个无监督的过程。在经典AE的基础上,一些“增强”的模型相继提出,如降噪自编码器(denoising AE, DAE)、卷积自编码器(convolutional AE, CAE)[26]等。其中,DAE的思想是通过随机的“擦除”输入的某些特征,迫使模型学习这些“破损”的输入数据进而获得更具泛化能力的模型。

图3是文献[25]中关于DAE模型的原理图。为了学习出一个更具鲁棒性的识别模型,本文选用“堆叠”多个DAE的SDAE模型对雷达信号进行自主特征学习。该DNN模型通过将前一层的DAE输出作为下一层DAE的输入,依次训练各DAE直到最后一层结束,则可以在顶层学习到输入的更抽象表示。

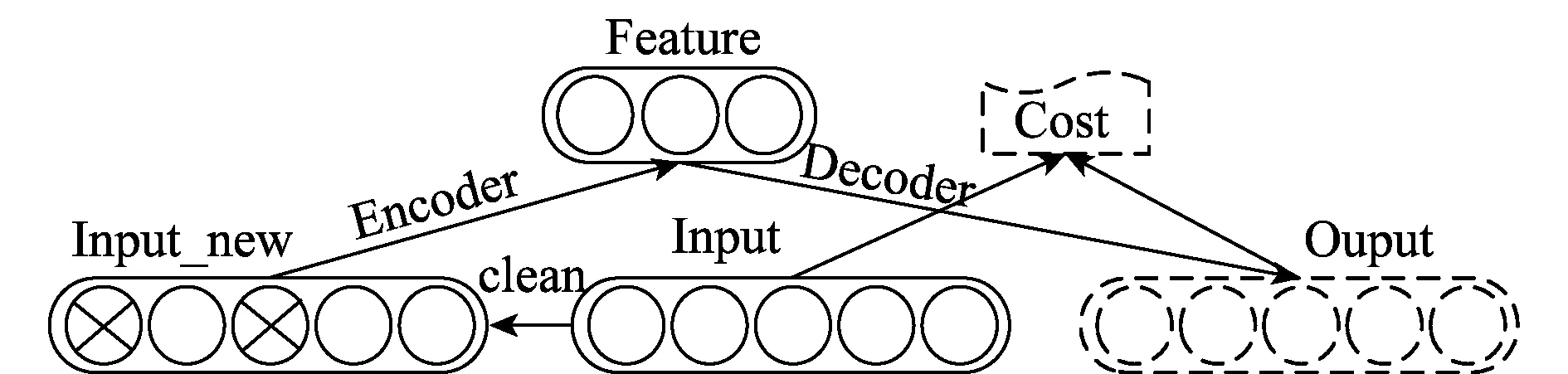
图3 DAE模型结构Fig.3 Model of DAE

2 多SVM分类器组合算法

SVM是一种基于统计学习理论的分类算法,它在许多模式识别和数据挖掘任务中被广泛应用。SVM分类器不仅具有较强的泛化能力,并且,对于线性不可分数据,可以通过核函数将数据映射到高维空间进行分类。常用的核函数有,线性核函数、高斯核函数、多项式核函数等等。目前,对于一个给定的分类任务,SVM核函数的选择仍然是一个研究的难点,而多SVM组合是解决这个问题的一个有效方法。因此,本文采用组合SVM分类器具有如下的优点:

(1) 根据上面的分析,组合SVM分类器可以避免核函数选择的问题;

(2) 基于不同核函数的SVM在相同的训练集上具有不同的性能,对它们的输出结果进行组合可以提高分类的性能。

2.1 分类器线性组合算法

多分类器组合算法是一种模型融合方法,它的基本思想是假设不同的分类器能为结果提供不同侧面的信息,通过融合这些信息就可以对最终的决策提供更好的支持。文献[27]提出了一种深度模型的线性集成的方法,该方法通过组合不同DNN模型的输出来训练一个HMM分类器,以此来获得比单一DNN模型更好的结果。本文在文献[27]的基础上,构造了一种基于后验概率的多分类器线性组合模型,具体描述如下。

考虑一个模式分类任务z,其中z可以被分配到c个模式类别中的一个,则待分类对象有c个模式类别{ω1,…,ωj,…,ωc}。令P=[p(x1),…,p(xi),…,p(xN)]T∈RN×c为N个样本的真实后验概率,p(xi)∈R1×c表示样本xi的真实后验概率为

p(xi)=[p(ω1|xi),…,p(ωc|xi)]

显然,xi属于某一类别的后验概率为“1”,反之为“0”。假设有M个分类器,可以用Pk=[pk(x1),…,pk(xi),…,pk(xN)]T∈RN×c来表示第k个分类器对N个样本的后验概率。其中,pk(xi)∈R1×c表示分类器k对样本xi的后验概率输出为

pk(xi)=[pk(ω1|xi),…,pk(ωc|xi)]

多分类器线性组合策略的基本思想是:组合模型判定样本属于某一模式类别的决策值是由多个分类器的输出决策值进行线性组合来获取的,可以形式化的描述为

p(ωj|xi)≈α1p1(ωj|xi)+…+αMpM(ωj|xi)+bi

进一步,多分类器的线性组合模型就可以描述为

(1)

式中,Wk∈Rc×c表示分类器的权值矩阵;bT∈Rc×1为偏置向量。对式(1)的参数进行估计使组合模型的输出值与真实值之间的差异最小,这个差异可以采用最小平方误差来衡量,即

∑i‖pcom(xi)-p(xi)T‖2

(2)

在参数估计问题中,为了避免模型过拟合,通常在其损失函数中加入正则化项[28]。考虑到模型参数的便于求解,为损失函数增加L2-正则化项,所以式(2)改写为

∑i‖pcom(xi)-p(xi)T‖2+

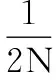
(3)

式中,γk是正则化参数,可以使用交叉验证的方法进行选择。式(3)是一个多元函数求极值问题,可以用最小二乘法进行求解。首先,通过求解W、bT的偏导数,即

则

解方程组可以解得:[WbT]=BA-1。其中,A和B的值分别为

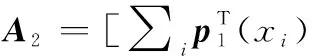
A3=[∑ip1(xi),…,∑ipM(xi)]

B=[PTP1,…,PTPM,∑ipT(xi)]

本文选择4种不同的SVM模型,分别是基于线性核的SVM(记为SVM_LK)、基于多项式核的SVM(记为SVM_PK),基于高斯核的SVM(记为SVM_GK),基于Sigmoid核的SVM(记为SVM_SK)。从效果上看,组合多SVM分类器可以在一定程度上避免了SVM核函数选择的问题。但是,标准SVM无法给出样本的后验概率输出,为了使用本文的线性组合算法,需要寻求一种SVM后验概率输出的方法。

2.2 SVM的后验概率输出

对于模式分类而言,标准SVM可以得到样本属于某一类别的决策值,却无法给出其相应的后验概率。但是,决策值和后验概率之间存在一定的关联性,样本的决策值绝对值越大表明其属于某一类别可信度越高,因此可以考虑用决策值获取样本的后验概率。可以采用Platt[29]提出的方法获得SVM的后验概率。该方法的本质是通过训练数据拟合出一个Sigmoid模型,该模型可以实现SVM的决策值到后验概率的映射。Sigmoid模型可以表示为

式中,f是SVM输出的决策值;参数A、B可以通过训练得出。应当注意的是,该方法只适用于二分类问题,对于多分类问题可以将其划为多个二分类问题,分别求出相应的后验概率后进行归一化处理[30]。

3 仿真实验和结论分析

通过仿真8种常见的RES信号来验证本文方法的有效性,包括具有恒定频率的常规信号、线性调频信号(linear frequency modulation, LFM)、非线性调频信号(nonlinear frequency modulation, NLFM)、二相编码信号(binary phase shift keying, BPSK)、二进制频率编码信号(binary frequency-shift keying, BFSK)、Chirp子脉冲步进频率信号(CSF)、多相编码信号(multiple phase shift keying, MPSK)和Costas编码信号。信号载频为100 MHz,采样频率为500 MHz,脉宽为1.8 μs。其中,BPSK和BFSK采用13位Barker码;CSF的步进频率10 MHz;MPSK采用16位Frank码;NLFM采用正弦波调制;Costas编码信号包含10个子码;BFSK的两个频率分别是100 MHz和20 MHz。在20～30dB的信噪比范围内,每种信号样式每隔5 dB产生10个脉冲信号,总计160个脉冲信号作为SDAE模型的训练样本。同时,分别在-5 dB、-2 dB、0 dB、2 dB、5 dB信噪比下各仿真800个脉冲信号作为测试样本,每一信号样式各100个脉冲。本次实验都是在MatlabR2015a+LibSVM 3.12平台下完成的,同时使用DeepLearnToolbox工具箱搭建所需的SDAE模型。选择LibSVM工具箱除了便于SVM模型的搭建外,并且该工具箱采用文献[29]提出的方法获得SVM的后验概率输出。

实验1为了验证SDAE特征学习的有效性,本文选用几种传统的人工提取的特征进行比较。如文献[3-4]提取了RES频域的复杂度特征,包括盒维数(box dimension, BD)、范数熵(norm entropy, NoEn)和稀疏度(sparseness factor, SF);文献[8]提取了RES的小波脊频级联特征(wavelet ridge-frequency cascade-feature, WRFCCF),该特征向量由小波脊频上的7维统计特征组成的。对于复杂度特征和WRFCCF,分别选择基于线性核函数的SVM和基于高斯核函数的SVM来获得最佳的识别效果。然后,构造含有3层隐含层的SDAE模型(784-100-100-100-8),模型的参数设置采用DeepLearnToolbox工具箱默认值,最后使用Softmax分类器进行分类。其中,SDAE模型的输入特征是RES的时频图像。各方法的分类平均正确率如表1所示。

表1的结果可以看出,基于SDAE模型提取的特征在较低SNR下表现出良好的性能,并比基于文献[3-4,8]提出的特征获得更高的正确率,其中在SNR=-2 dB条件下仍有大于83%的准确率;基于复杂度参数的方法效果较差,主要原因是复杂度参数刻画信号波形的信息,在较低SNR下波形失真较为严重;同样的,基于WRFCCF特征的方法在SNR=5 dB也只有69%左右的准确率,表现出对噪声的敏感性。

实验2为了验证多SVM组合模型能有效提升RES识别正确率,本文提取实验1中SDAE模型的最后一个隐含层的输出值作为各对比分类器(SVM_LK、SVM_PK、SVM_GK、SVM_SK)的输入特征(参数设置采用LibSVM工具箱默认值)。同时,依据第2节描述的算法,组合这4种不同SVM进行对比,实验结果如表2所示。

表2 不同SVM的分类正确率比较

从表1和表2可以看出,基于线性核函数的SVM相较于传统的Softmax分类器在分类正确率上均有一定程度地提升(除了SNR=-2 dB的情况),而本文提出的组合模型能获得了比其他4种SVM分类器具有更好的效果。图4是不同分类模型在不同信噪比下对8种雷达信号的分类正确率曲线,容易看出SVM_PK、SVM_PK、SVM_LK和SVM_SK这4个不同的SVM分类器在分类性能上非常相近,其中,SVM_LK的分类性能最好。同时,通过对比图4中的性能曲线可以看出,组合这4种SVM的集成模型获得了更好的分类正确率。

图4 不同SNR下8种RES的识别率Fig.4 Recognition result of 8 types of RES in different SNR

最后,为了进一步对各分类模型的性能进行对比,构造一个测试集进行测试,包含上述实验中信噪比在-5～5 dB的所有信号。表3是6种不同分类模型对测试集的分类正确率,从表中可以看出,相较于SDAE+Softmax模型,本文的组合模型可以提高2个百分点的分类正确率。并且,该组合模型也能获得比单独使用SVM进行分类更好的性能。

表3 分类正确率比较

4 结 论

本文提出了一种基于深度学习和集成学习的融合模型,并应用于RES的分类识别,并通过仿真8种常见RES信号进行验证。实验1的结果表明了相较于文献[3-4,8]提取的传统人工特征,本文基于SDAE模型提取的RES特征获得更高的正确率。根据实验2的结果可以得出:MSVMLC模型能进一步提升RES识别性能。另外,值得注意的是,基于DNN模型提取的特征参数难以解释其物理意义,并且DNN模型的训练通常需要大量的有标签数据,因此需要完备的RES数据作为支持。