不同注浆阶段矩形盾构隧道衬砌结构的力学性态研究
2018-11-09王新新
王新新
上海建工集团工程研究总院 上海 201114
近年来伴随城市地下空间开发的迅猛发展,盾构法施工应用越来越广泛。特别是矩形盾构隧道因相比圆形隧道具有显著的空间断面利用率高、安全埋置深度浅、土地占用率低等优点,在工程中得到了越来越多的应用。然而,矩形盾构隧道受力相比圆形隧道存在受力较不均匀的缺点,在各种施工荷载作用下局部会产生较大弯矩与剪力。因此,研究施工期各种施工荷载对矩形管片结构受力特性的影响已迫在眉睫[1-2]。
目前,对矩形盾构管片施工期受力特性的研究较少,主要采用模型试验法和现场实测法。张冠军等[3]通过国内首台6 m×4 m大断面矩形隧道拼装式管片结构承载力试验,分析了大断面矩形管片的受力情况,得到矩形管片在结构设计荷载下管片的弯矩和变形规律。杨方勤等[4]建立了考虑衬砌接头刚度的梁-弹簧计算模型,为了验证矩形管片刚度、强度是否满足设计要求,进行了矩形衬砌管片1∶1三环结构试验。孙巍等[5]系统性研究了大断面矩形盾构法隧道衬砌受力的影响因素,其中注浆荷载对矩形盾构法隧道受力影响较大,需要与施工工艺结合来合理地确定注浆荷载。王东方等[6]以结合宁波类矩形盾构隧道研究了施工同步注浆对衬砌结构力学特性的影响。
施工阶段隧道衬砌管片的约束条件复杂,且存在较多影响因素[7]。因此,本文结合现场工程采用理论分析、数值仿真与现场实测相结合的方法研究不同注浆阶段矩形盾构隧道衬砌结构力学性态,为后续施工提供指导。
1 工程概况
某地下通道工程全长470 m,其中下穿高架段采用矩形隧道施工法,盾构段长度为83.95 m。隧道衬砌结构每环由6块复合管片拼装而成,在管片的纵向与环向都采用直螺栓的连接形式通缝拼装,其具体的结构参数为:结构内部净空宽8.65 m、高3.85 m,扁平率0.44,衬砌厚度0.55 m,拱顶起拱量0.15 m,拱腰起拱量0.10 m(图1)。

图1 矩形衬砌结构单元效果图
2 矩形隧道衬砌内力理论解析
2.1 矩形盾构隧道计算模型
考虑矩形盾构隧道衬砌由若干管片拼装通过螺栓连接而成,接头具有非连续性的特点,为模拟管片接头刚度,降低对衬砌环整体刚度的影响,本文采用隧道设计中常用的荷载结构模型(梁-弹簧模型)。其中,管片被离散为梁单元,管片环向接头由转动弹簧kθ、轴向弹簧kn、剪切弹簧ks三部分组成(图2)。图2中H0为地下水位至地面的距离;H为隧道顶部覆土厚度;q1为隧道顶部的水土荷载;q2为隧道底部的水反力(水土分算时);e1,e2分别为隧道顶部与底部的侧向水土压力;g为衬砌自重;kr为地层抗力综合系数,包括径向和剪切刚度系数。

图2 梁-弹簧模型
2.2 地质参数及理论分析参数
2.2.1 地质参数
隧道覆土厚度为7 m,位于②3灰色粉砂、③灰色淤泥质粉质黏土、④灰色淤泥质黏土之中,土层分布及力学特性如表1所示。

表1 隧道周边土层分布及力学特性
根据地质报告,工况中假定地下水埋深为地表下0.5 m。
2.2.2 理论计算参数
1)管片材料弹性模量E=2.5×108kPa,转动惯量I=1.4×10-2m4,截面面积A=0.546 m2。
2)管片接头采用线性接头模式,弯曲转动刚度kθ=4×104kN·m/rad,轴向压拉刚度kn=104kN/m,剪切刚度ks=2×104kN/m。
3)地层弹簧系数:地层法向刚度Kn=2.4×104kN/m,切向刚度Ks=1.2×104kN/m。
2.3 理论解析结果
为简便计算考虑,理论计算中将计算截面近似等效于9.75 m×5.00 m的矩形截面,不考虑衬砌断面的起拱(图3)。
理论解析结果如表2所示。

图3 内力解析截面

表2 衬砌理论解析结果
3 矩形隧道衬砌内力有限元数值分析
3.1 矩形衬砌模型
采用通用有限元分析软件Plaxis进行隧道开挖过程中衬砌变形的有限元数值模拟,土体采用Mohr-Coulomb弹塑性模型,衬砌采用线弹性模型(图4)。为确保与理论分析时研究对象的一致性,模型尺寸取宽56 m、深30 m,矩形衬砌尺寸取9.75 m×5.00 m(不考虑衬砌断面的起拱)。

图4 矩形隧道开挖模型
3.2 工况设置
3.2.1 未注浆阶段
未注浆阶段主要分析衬砌环安装完毕,在水土压力情况下的变形(图5)。
3.2.2 注浆阶段
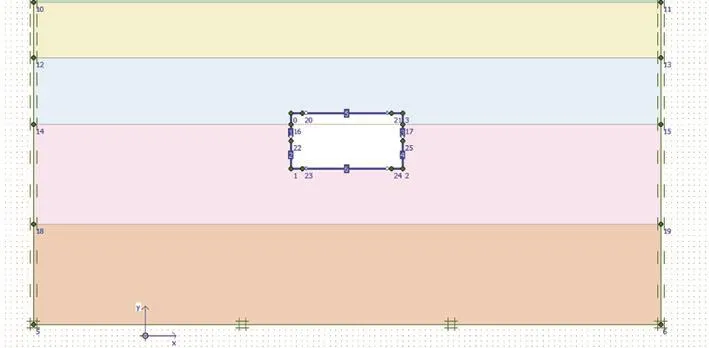
图5 未注浆阶段模拟
研究衬砌环注浆过程中在外界水土压力和注浆压力作用下的变形。目前,针对注浆压力的研究有很多,但相关设计规范并没有对其进行具体规定。在日本盾构隧道设计规范中,壁后注浆压力一般比泥水压力大50~ 100 kPa。在上海长江隧道工程设计中,采用的荷载分布模式为三角形分布,国际隧道协会也同样推荐采用三角形分布模型。在综合以上研究及考虑矩形盾构注浆设备能力的基础上,注浆荷载采用三角形分布进行模拟,以注浆孔为中心两边分布宽度取1 m,注浆压力取实际值0.08 MPa(图6)。

图6 注浆模拟
3.2.3 浆液凝固阶段
在注浆完毕12~20 h,浆液开始凝固,注浆压力逐渐消散。在浆液凝固后,衬砌环只承受水土压力作用。然而需要注意的是,衬砌环周围土体由于水泥浆的掺入,其抗剪强度及本身重度将明显增加,本身体积也会有所膨胀。在本次模拟中,通过改变盾构周围土体力学性质来模拟土体抗剪强度和重度的增加,通过对注浆影响土体设置膨胀率来模拟土体体积的膨胀。对于注浆影响土体范围,相关研究不少,同济大学白云教授通过室内模型试验,认为同步注浆影响范围集中在注浆孔周围2~3 m范围内。本次模拟假定注浆影响范围为开挖面之外2.5 m(图7)。鉴于现场每环注浆量为6 m3,土体膨胀率为6%左右。

图7 浆液凝固模拟
3.3 计算结果分析
3.3.1 未注浆阶段
从矩形盾构土体开挖后周边土体沉降变化〔图8(a)〕可以看到,盾构周边土体最大隆起32 mm,地表沉降36 mm。衬砌管片〔图8(b)〕下边隆起约28 mm,呈现中间隆起大于两边隆起的特征,衬砌上边隆起约8 mm,呈现两边隆起大于中间隆起的特征。衬砌最大弯矩位于衬砌下边中央,约857 kN·m/m,衬砌上边中央弯矩为838 kN·m/m〔图8(c)〕。最大剪力为衬砌的四个角部,下面两角剪力为532 kN/m,上面两角剪力为523 kN/m〔图8(d)〕。
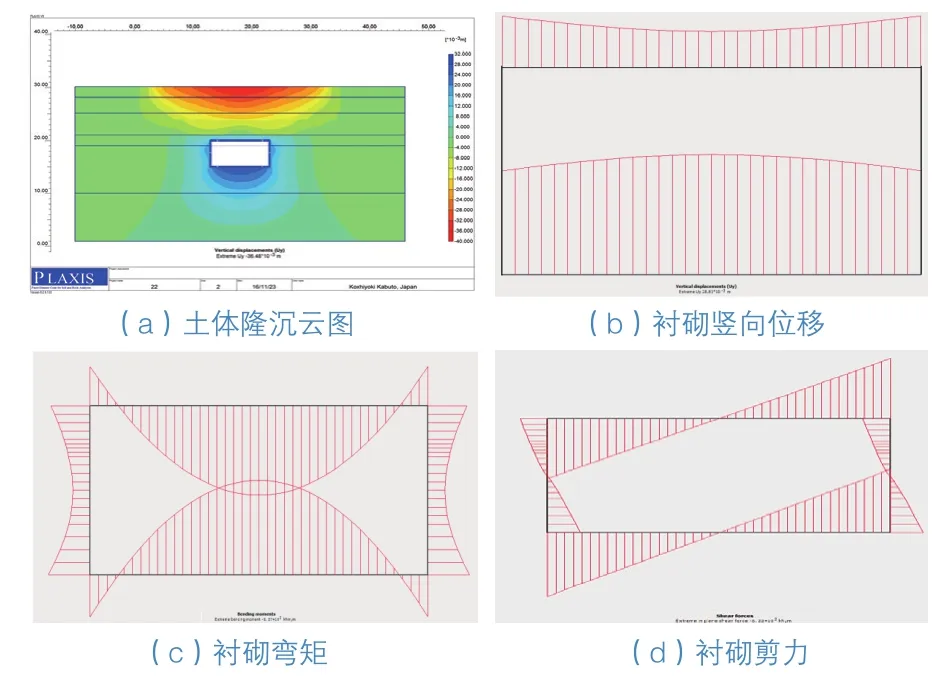
图8 未注浆阶段数值模拟
3.3.2 同步注浆阶段
同步注浆过程中衬砌管片下边缘衬砌中央隆起约29.66 mm,上边缘衬砌中央隆起9.1 mm,与未注浆阶段比较,可以得到同步注浆使得衬砌下边发生1.66 mm变形,上边发生1.1 mm变形;衬砌下边呈现中间隆起大于两边隆起的特征,上边呈现两边隆起大于中间隆起的特征〔图9(a)〕。衬砌最大弯矩位于下边缘衬砌中央,约912 kN·m/m,与未注浆相比,增加了55 kN·m/m,上边缘衬砌中央弯矩为901 kN·m/m,增加了63 kN·m/m〔图9(b)〕。最大剪力为衬砌的四个角部,下面两角剪力为614 kN/m,增加了82 kN /m,上面两角剪力为603 kN/m,增加了80 kN/m〔图9(c)〕。

图9 注浆阶段数值模拟
3.3.3 浆液凝固后
浆液凝固后,盾构周边土体最大隆起24 mm,地表沉降32 mm〔图10(a)〕。注浆过程中衬砌管片下边缘中央隆起约22.7 mm,上边缘衬砌中央隆起8.3 mm,与注浆阶段比较,可以得到浆液凝固使得衬砌下边发生6.96 mm下沉,上边发生0.8 mm下沉;衬砌下边呈现中间隆起大于两边隆起的特征,上边呈现两边隆起大于中间隆起的特征〔图10(b)〕。衬砌最大弯矩位于下边缘衬砌中央,约855 kN·m/m,与注浆阶段相比,下降了57 kN·m/m,上边缘衬砌中央弯矩为832 kN·m/m,下降了69 kN·m/m〔图10(c)〕,最大剪力为衬砌的四个角部,下面两角剪力为580 kN/m,下降了34 kN/m,上面两角剪力为573 kN/m,下降了30 kN/m〔图10(d)〕。

图10 浆液凝固后数值模拟
4 矩形盾构隧道装配式衬砌变形反分析
由于管片制作误差等因素影响,将实际衬砌变形监测值和设计图纸尺寸进行比较从而计算衬砌变形量是不严谨的。因此,采用基于三维激光扫描技术的矩形盾构隧道全截面监测方法,将三维扫描监测数据和三维虚拟拼装数据进行了比较,获取了注浆阶段和浆液凝固阶段的衬砌实际变形,并通过数值模拟进行了位移反分析,从而排除了管片制作误差导致的衬砌尺寸偏差,更能反映衬砌受力后的真实变形状态。
4.1 不同注浆阶段矩形隧道衬砌实测变形对比
4.1.1 管片未注浆阶段
从预拼装尺寸和未注浆阶段管片实际尺寸比较(图11)可以看到,在实际安装后,衬砌上下边与预拼装尺寸基本一致,误差仅2 mm左右,但由于存在橡胶止水和施工误差因素,实际尺寸均比预拼装有所增大,整体呈现外扩状况。
4.1.2 管片同步注浆阶段
从预拼装尺寸和注浆阶段管片实际尺寸比较(图12)可以看到,在承受注浆压力后,衬砌上下边发生明显内弯。由于并非对称注浆,衬砌变形并不对称,衬砌上下边左半部分变形量大于右半部分,下边变形量大于上边,上下边最大变形量分别14 mm和15 mm,两侧有1~3 mm外扩。

图11 安装阶段管片尺寸偏差(管片安装完3 h)

图12 注浆阶段管片尺寸偏差 (管片出盾尾阶段)
4.1.3 浆液凝固后
从预拼装尺寸和浆液凝固后管片实际尺寸比较(图13)可以看到,在注浆结束后,衬砌上边左部和下边有2 mm左右回弹,两侧变化不明显。
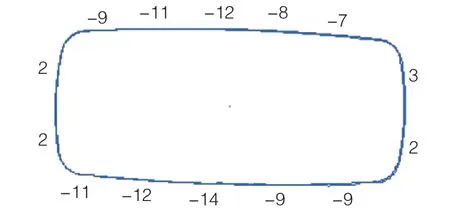
图13 浆液凝固阶段管片尺寸偏差(管片安装完3 d)
4.2 矩形盾构隧道装配式衬砌管片力学反分析
考虑到本工程采用同步注浆,管片出盾尾和注浆同时发生,故在反分析中不考虑单纯承受水土压力的工况,仅计算注浆阶段和浆液凝固后2种工况。
4.2.1 计算模型
采用通用有限元分析软件Plaxis进行隧道开挖过程中衬砌变形的有限元数值模拟。本构模型、单元模型、模型边界条件、转动刚度的设置与3.1节一致。
将4.1节中监测得到的实际管片变形作为限定位移施加在衬砌梁单元上(图14)。

图14 衬砌位移限定(注浆阶段)
4.2.2 衬砌管片力学性态反分析
1)管片注浆后,最大弯矩位于衬砌下边靠左0.7 m左右,大约为980 kN·m/m,最大剪力位于衬砌左下角,大约为677 kN/m(图15)。与有限元数值计算结果进行比较,弯矩值增大了约7.5%,剪力值增大了10.2%。弯矩最大值也向左偏离0.7 m左右。分析其差异原因,主要有2条:

图15 注浆阶段衬砌管片应力反分析
① 实际过程中并非对称注浆,注浆压力及浆液量衬砌左右两边有明显差异,从而导致衬砌环受力不对称,最大弯矩值位置发生偏移。
② 理论分析中管片之间转角刚度采用经验值,实际工程中转动刚度受螺栓直径、材料以及紧固力影响。两者之间会有一定区别。
2)浆液凝固后,最大弯矩位于衬砌下边靠左0.7 m左右,大约为922 kN·m/m,最大剪力位于衬砌左下角,大约为623 kN/m(图16)。同样,由于注浆位置和管片间转动刚度因素,反分析结论与有限元数值计算结果有所差异,弯矩值增大了约7.8%,剪力值增大了7.4%。弯矩最大值也向左偏离0.7 m左右。
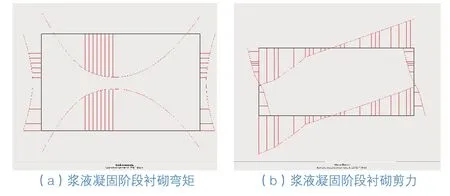
图16 浆液凝固阶段衬砌管片位移反分析
4.3 结果对比分析
将矩形盾构施工期的弯矩和剪力计算结果进行汇总,如表3所示。
1)有限元数值计算结果与理论解对比结果如下:
① 在只考虑水土压力情况下,理论解析和数值模拟结果基本相符,使用梁-弹簧模型能较为准确地反映衬砌受力情况。两者比较而言,角部剪力值相差较小,中央弯矩有5%~10%的区别。
② 注浆阶段由于受到注浆压力作用,衬砌所受弯矩和剪力有所增加,弯矩增加幅度为8%左右,剪力增加幅度为15%左右。
③ 浆液凝固后,注浆压力逐渐消散,衬砌所受弯矩和剪力有所减少,但由于浆液填充效果的存在,衬砌所受弯矩和剪力仍比开挖阶段的大。
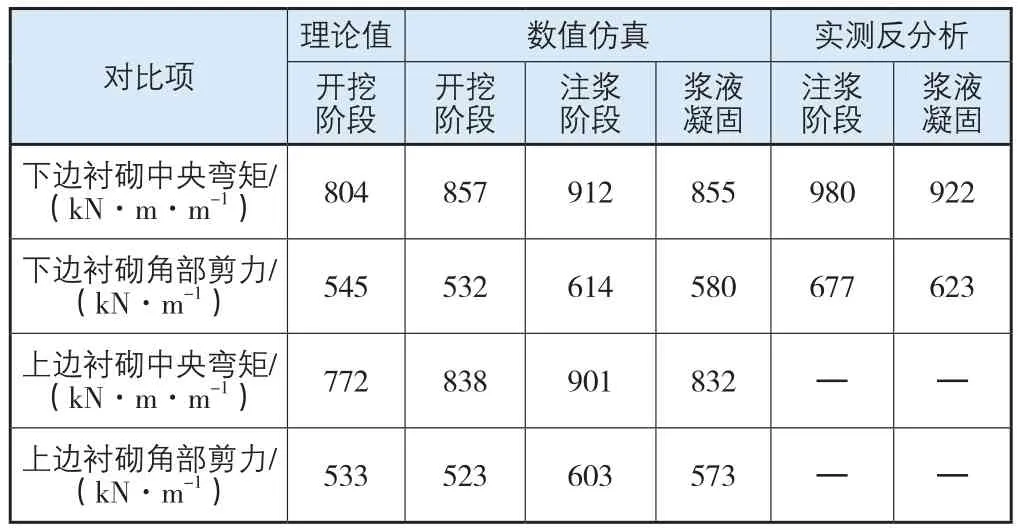
表3 施工期矩形衬砌结构受力对比汇总
2)现场实测数据及其位移反分析结果与有限元数值计算结果对比如下:注浆阶段最大弯矩位于衬砌下边靠左0.7 m左右,大约为980 kN·m/m,最大剪力位于衬砌左下角,大约为677 kN/m。浆液凝固阶段最大弯矩位于衬砌下边靠左0.7 m左右,大约为922 kN·m/m,最大剪力位于衬砌左下角,大约为623 kN/m,与有限元数值计算模拟结果相比,均增大了7%~10%,这一差异应当是注浆孔位不对称及转动刚度设置有所偏差所致。
5 结语
本文结合现场工程采用理论分析、数值仿真方法和现场实测研究不同注浆阶段矩形盾构隧道衬砌结构的力学性态。研究表明,梁-弹簧模型能较为准确地反映矩形衬砌施工期的受力情况,由于注浆作用导致衬砌所受的弯矩和剪力增大,施工中应注重注浆阶段衬砌管片力学性态的监控,确保施工安全。
