基于改进PID控制的折弯送料机器人运动轨迹误差仿真研究

2018-11-09

佳木斯大学学报（自然科学版） 2018年5期

(安徽中佳自动化科技有限公司，滁州 239000)

0 引言

钣金折弯加工是现代机械制造的重要环节，广泛应用于机床、汽车、家电及航天等领域。传统钣金折弯送料采用人工操作，导致加工效率下降、定位不准确、产品性能差等许多问题[1～2]。折弯机在进行钣金折弯时，需要和机器人密切配合，建立实时通讯和感应，完成一系列动作。折弯机构需要机器人自动化取料和送料、板材定位和板材翻面等功能，使压力机构快速的完成折弯动作，从而完成钣金件的加工。因此，研究折弯送料机器人运动轨迹精度对于促进钣金件加工的发展具有重要的意义。

文献[3]研究了折弯送料机器人折弯运动模型，通过MATLAB软件对运动模型进行仿真验证，能够提高折弯送料机器人加工效率。文献[4]研究了折弯送料机器人路径规划控制方法，通过MATLAB软件对理论运动轨迹进行仿真验证，提高了折弯送料机器人运动轨迹跟踪精度。但是，对于高精度定位要求的钣金件，折弯送料机器人运动轨迹的误差很难满足设计要求。对此，通过遗传算法优化折弯送料机器人增量式PID控制器参数变量，通过MATLAB软件对跟踪误差进行仿真验证，输出角位移误差变化曲线，为深入研究折弯送料机器人送料定位误差提供参考价值。

1 机器人简图

折弯送料机器人简图如图1所示，机器人末端执行器将板材吸住，然后送到下模上面，冲压机床带动上模上下运动，完成对板材的折弯工序。

图1 折弯送料机器人简图

在图1中，q1、q2、q3为连杆运动的角位移，m1、m2、m3为连杆的质量，l1、l2、l3为连杆的长度。

2 改进PID控制

2.1 增量式PID控制

在控制系统应用中，最常见的控制方法是PID控制，PID控制根据误差的比例、积分和微分对受控对象进行在线控制。采用增量式PID控制[5～6]规律公式为：

(1)

式中：Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

2.2 改进PID控制

PID控制过程中，会产生滞后和超调现象。对此，对PID控制参数进行优化。通过在线检测系统输出误差决定控制参数，其控制结构如图2所示。

图2 遗传算法优化PID控制过程

自适应遗传算法通过选择、交叉和变异概率可以对PID控制参数Kp、Ti、Td进行在线优化，具体优化过程如下所示：

1)编码：采用二进制对参数Kp、Ti、Td进行编码，将优化参数转换为编码方式。通常选择10位无符号二进制表示，对控制器参数进行寻优，编码后基因的长度为30，控制器参数编码[7～8]后如下所示：

[Kp1,Kp2,…,Kp10,Ti1,Ti2,…,Ti10,Td1,Td2,…,Td10]

(2)

2)初始化种群：在取值区间内随机生成M个字符串，每个字符串表示一个个体。生成的M个个个体组成种群，遗传算法通过M个字符串进行迭代。初始种群为：

(3)

3)适应度函数：适应度函数反应个体对环境适应能力的强弱，与选择目标函数相关。控制系统指标主要包括稳定性、准确性和快速性。因此，采用的目标函数[9]为：

(4)

式中：e(t)为理论值与实际值误差；u(t)为控制器输出；tu为上升时间；ω1、ω2、ω3为权值。

适应度函数为：

(5)

4)选择：选择操作是对群体进行筛选，选择适应度好的个体遗传到下一代。选择操作采用比例选择算子运行，每个个体选中的概率为：

(6)

5)交叉和变异：交叉概率和变异概率会影响到遗传算法搜索结果。交叉概率较大会导致适应度个体结构损坏，交叉概率较小会带着搜索速度变慢。变异概率较大，遗传算法收敛慢，变异概率较小，获得最优解较男。因此，调整公式[10]如下：

(7)

(8)

式中：fmax为种群适应度最大值；favg为种群适应度平均值；fc为交叉个体适应度值；fm为变异个体适应度值；k1、k2、k3、k4为概率系数。

6)解码：搜索到最优解后，进行解码。以Kp为例，解码操作[12]如下所示：

(9)

式中：X1为遗传空间的比例系数。

PID控制参数调优流程图如图3所示。

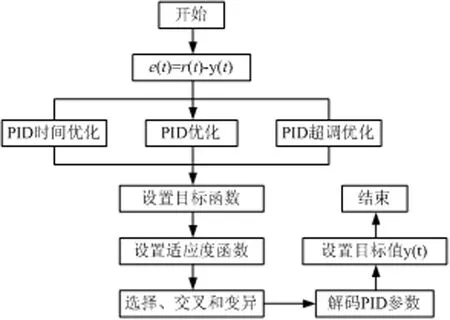
图3 PID参数调优流程

3 仿真与分析

折弯机器人控制参数变量采用遗传算法进行优化，设样本个数为30，遗传代数为100，交叉概率和遗传概率初始值为Pc=0.8，Pm=0.02，仿真时间为8s。优化前与优化后，其运动轨迹误差仿真结果如图4所，图5和图6所示。

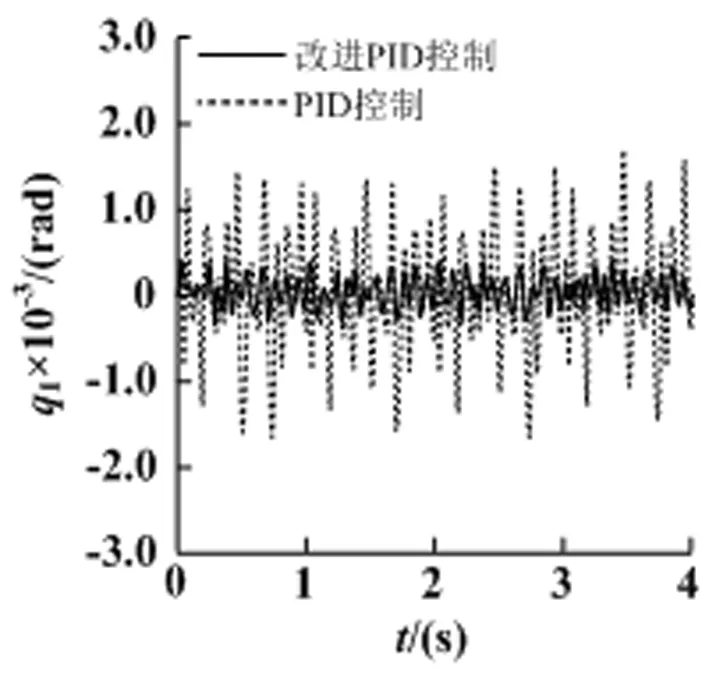
图4 连杆1角位移误差

图5 连杆2角位移误差

图6 连杆3角位移误差

由图4、图5和图6可知：优化前，连杆1、连杆2和连杆3运动角位移产生的最大误差为1.73×10-3rad、1.91×10-3rad和2.03×10-3rad；优化后，连杆1、连杆2和连杆3运动角位移产生的最大误差为0.42×10-3rad、0.48×10-3rad和0.55×10-3rad，角位移最大误差分别下降75.7%、74.9%和72.9%。另外，误差整体波动幅度较小。因此，采用遗传算法优化折弯送料机器人控制变量参数，能够提高机器人运动轨迹跟踪精度，从而提高了送料板材的定位精度。