初中数学习题教学与创新思维培养

常 青

(江苏省南京市雨花台中学 210000)

一、发挥出习题的思维示范作用

教师在对习题内容与方法进行安排时，首先应当考虑到习题对于思维创新的示范作用.无论是例题还是习题，均需要展示出其在知识和技能应用方面的通用处理办法，以便使学生可以借此实现思维的引申拓展，收到举一反三的效果.当然，在提供并讲解这类习题时，初中数学教师需要充分考虑到学生所处的实际认知状态，以面向全体学生为基准，同时不能忽略学生之间存在的客观个性差异，使习题既少且精，以鲜明的代表性突出教学的重点和难点，特别是要考虑到示范思路的引领效果，方便融入情境、启迪于设问，让学生走向对知识的更深刻、更全面认知境界.例如当接触到相似三角形有关内容时，教师可以给学生提供如下典型习题：现在已知△ABC里面，点D与点E分别为边AB与边AC上的点，请再补充一个条件，从而使△ADE相似于△ABC.这个问题非常具有典型性，因为它一方面注意到了习题的示范作用，同时也考虑到了学生的个性化要求，即可以是△ADE与△ABC相似，也可以是△AED与△ABC相似，补充条件时可以是角对应相等，还能够让边对应成比例.当教师给出类似的习题以后，一定要给学生提供充分的审题与思考时间，以便使学生更主动思考问题与基础知识的关联，并保证学生的思维个性张扬.

二、展现出习题的变式可能性

在对学生创新思维进行培养时，教师需要注意到学生的思维广度与多维度的同时训练，也就是要让学生在富有想象力激发可能性的环境下，尝试从不同多角度进入问题，从而使问题解决过程更富探究效果.为此，教师需要注意到习题的变化，将原题变为富有开放性色彩的问题，或者是借助恰当变式训练，增加一题多变训练机会，以此增加知识迁移的可能性，促进学生求知欲望的增加.比如下面的问题：已知二次函数y=x2+mx+m-2，求证：不管实数m取何值，二次函数的图象始终经过定点.对于这样的论证问题，如果依照传统的思维方法，关注重点应当在于对过定点的证明方面，这样会限制学生的思维创新发展，而若是依拓展解题的新思路进行引导，则学生会得到思维潜能的激发.具体解决过程中，首先提出问题，已经明确与x相关的二次函数y=x2+mx+m-2，在x所取实数值不同时，其二次函数的共同特征是怎样的？接下来使学生随机代入实数值，并深入观察分析，从中总结出相应的规律性内容，之后学生可以给出结论：所有图象都具有开口向上的特点，且均和x轴有两交点，与此同时，全部图象均过定点.因为这些结论来源于学生自己的观察和思考，因此其对于问题的求知欲望得到了强化.

三、促进习题应用作用的发挥

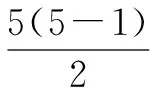
在初中数学教学过程中，习题教学是相当关键的环节所在，对于教学质量的提升以及学生能力的进步具有非常重要的作用，特别是如果应用得当，可以保证学生在此期间得到思维创新方面的有效培养.为此，教师一定要充分关注习题教学的优化问题，一方面注意到习题的示范作用，另一方面注意到习题的变式应用，除此以外还应当使学生将习题与实际应用相结合，借以增强习题的典型性与针对性，从而为巩固课程教学成果服务.