Feigenbaum-Kadanoff-Shenker方程带双参数的推广

刘好斌， 石勇国 *

（1.内江师范学院数学与信息科学学院，四川内江641100；2.内江师范学院数据恢复四川省重点实验室，四川内江641100）

在 1978 年，Feigenbaum［1］研究发现在含参数区间映射进行迭代时，出现了周期倍增的现象.为了解释这种普遍现象，Cvitanovic和Feigenbaum提出了函数方程

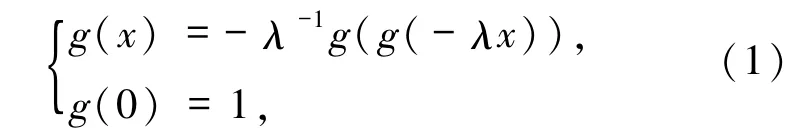
其中，λ∈（0，1）是参数，g：［-1，1］→［-1，1］是未知函数.该方程后来被称作Cvitanovic-Feigenbaum方程或简称Feigenbaum方程.诸多学者对该方程进行了研究：Feigenbaum［2］证明了解的存在性，Campanino等［3］扩大参数的取值并证明了方程有C2凹解，Lanford［4］利用不动点定理证明了解析解的存在性等，但这些证明方法都是非构造性的.在1985年，杨路等［5］提出了第二类Feigenbaum函数方程

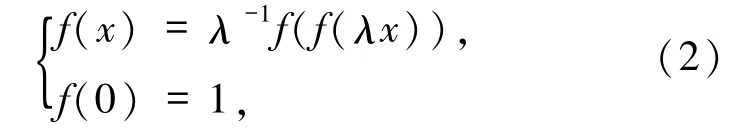
其中，λ∈（0，1）是参数，f：［0，1］→［0，1］是未知函数，并论证了方程（1）与（2）的等价性和给出了2种构造其单谷连续解的可行方法.在此基础之上，廖公夫［6］探讨了方程（2）由单谷映射扩充所能得到的一切连续解的形态，并给出了这类解的可行方法；唐元生［7］讨论了Feigenbaum函数方程的单峰偶解，并获得了方程（1）的单峰偶解是连续可微解，

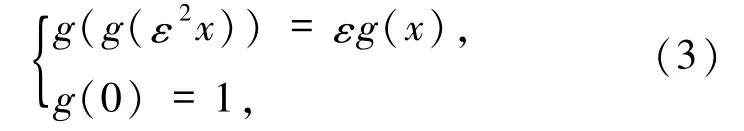
其中，ε∈（-1，0）是参数，g：［0，1］→［-1，1］是未知函数，他们讨论了FKS方程的解析解和奇异解.本文在文献［9-10］的基础上，讨论FKS方程带2个参数形式的推广以及Ck解的一些较文献［5］更为广泛的条件；司建国等［8-9］研究了第二类 Feigenbaum函数方程的C2凸的单谷解，并利用新的构造性方法讨论推广后的方程的单谷连续解的存在性与唯一性.此外，Briggs等［10］研究了 Feigenbaum 方程与 Feigenbaum-Kadanoff-Shenker方程（简称FKS方程）

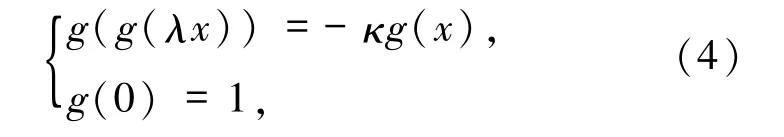
其中，0 ＜ κ2≤λ ＜κ ＜1，g：［0，1］→［-1，1］是未知函数.显然，方程（3）是当κ2＝λ时的特例.本文将利用迭代构造法，给出所有这类推广的KFS方程的连续严格递减解.

1 预备知识

关于这类推广的KFS方程的连续严格递减解，有如下的性质.

引理 1.1 设 g是方程（4）的连续严格递减解，且0＜κ2≤λ ＜κ ＜1，则：

（i）g（1）＝ - κ，g2（λ）＝ κ2；

（ii）g有唯一零点 α∈（0，1），且 g（λα）＝ α，α≥λ；

（iii）设 ψ（x）＝g（λx），x∈［0，1］，有唯一的周期点 α，即 ψ（α）＝α，且 g（λα）＝α；

（iv）g（x）＝ -κx在［λ，1］上有唯一解 x＝1；

（v）g（λ）≥λ2.

证明 对于（i），将 x＝0代入方程（4）中，得g（1）＝ -κ.再将 x＝1代入方程（4）得

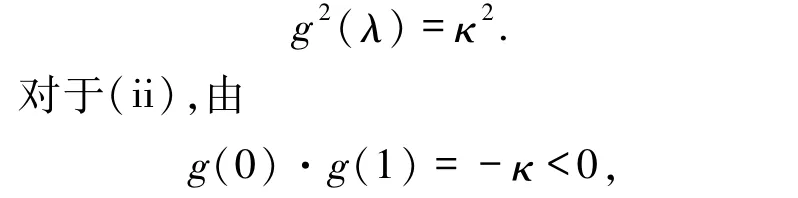
g为连续严格递减函数，故有唯一零点α∈（0，1），g（α）＝0.将x＝α 代入方程（4）得

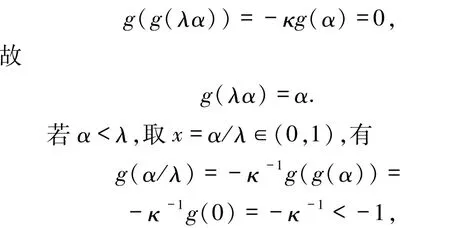
矛盾.故α≥λ.

对于（iii），假设 x0∈［0，1］有

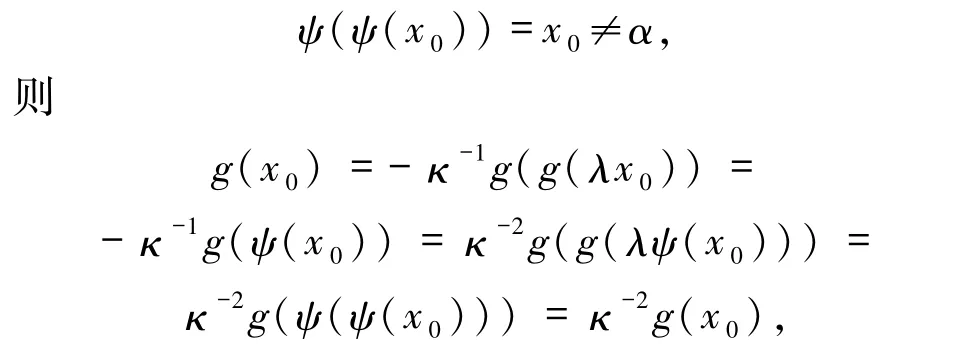
所以 κ2＝1，矛盾.因此 x0＝α，故 （iii）成立.

对于（iv），显然 x＝1是 g（x）＝ -κx的解.

假设 x＝ξ∈（0，1）也是方程

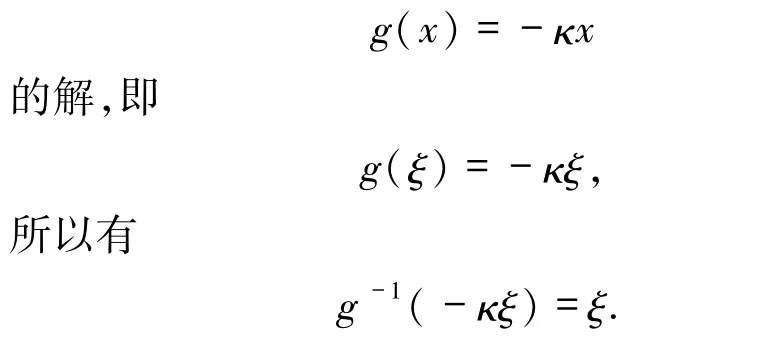
由g（0）＝1，g（1）＝ -κ，g是连续严格递减函数，则存在 γ∈（0，1），使得 g（γ）＝ ξ.由方程（4），取x＝γ，则

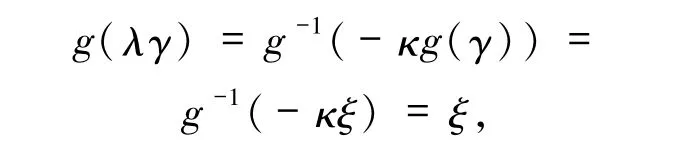
而g是连续严格递减函数，这与g（γ）＝ξ矛盾，因此（iv）成立.

对于（v），由 α≥λ ＞0，则 αλ≥λ2.由 κ2≤λ，g是连续严格递减函数，则

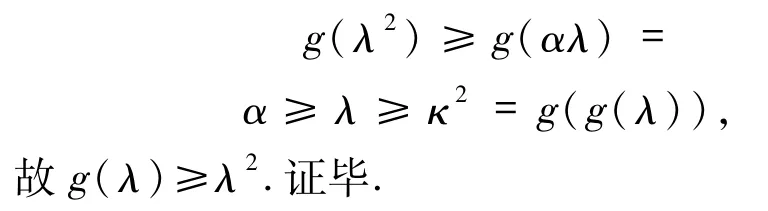
2 连续的严格单调递减解的构造方法

先考虑λ≤g（λ）.下面定理给出了连续严格单调递减解的构造方法.

定理 2.1 设 a＝g（λ），λ≤g（λ）.设

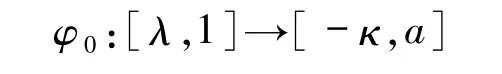
的连续严格单调递减的函数，满足：

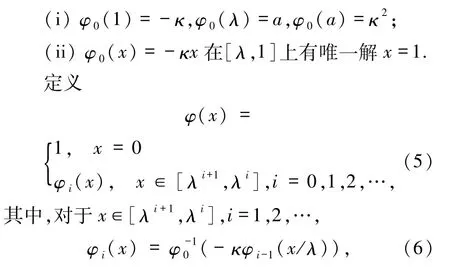
则φ是方程（4）的连续严格单调的递减解.反过来，如果φi是方程（4）的严格单调递减解φ在区间［λi+1，λi］上的限制，则条件（i）、（ii）以及（5）和（6）式均成立.

证明 由（i）可知

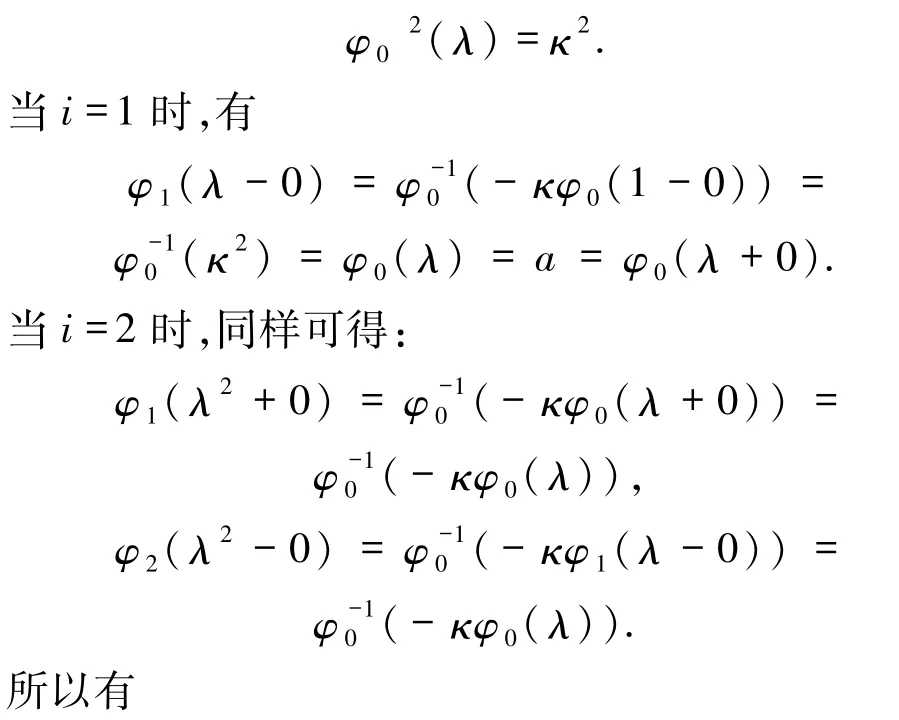
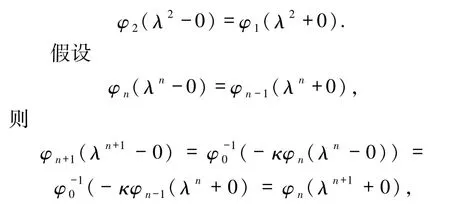
则 φ 在（0，1］上是连续的.根据 φ 在（0，1］上是连续严格单调的有界函数，则φ（x）存在，设为 ξ，所以有

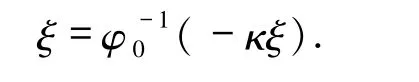
由（ii）可知 ξ＝1.故 φ 是方程（4）的连续的严格单调递减解.

反过来，如果φi是方程（4）的严格单调递减解φ 在区间［λi+1，λi］上的限制，根据引理 1.1，则条件（i）、（ii）以及（5）和（6）式均成立.证毕.

根据引理1.1（v），讨论满足条件

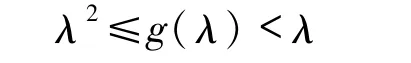
的连续严格递减解的构造方法.

引理2.2 设g是方程（4）的连续严格单调递减解，并且 κ2≤λ，λ2≤a＜λ，其中 a ＝g（λ）.令

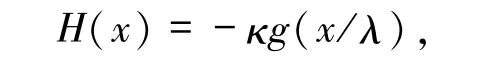
有如下事实：

（i）g（a／λ）＝ -g（κ2）／κ；

（ii）H在区间［0，λ］上是连续的严格单调递增的映射，并且 H（0）＝ -κ，H（λ2）＝ -κa且H（λ）＝κ2≤λ；

（iii）若x＝b＜λ是H最小的不动点，则λ2＜b＜λ，且H是从区间［b，λ］上严格递增的自映射.

证明 根据方程（4）有

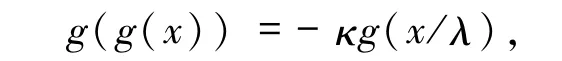
将x＝a代入这个方程，得

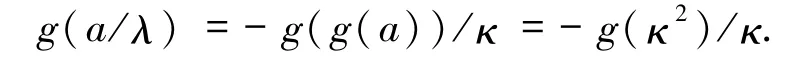
于是（i）成立.根据条件直接可以得到（ii）.若 x＝b＜λ是H最小的不动点，根据（ii）得

λ2＜ b ＜ λ， H（b）＝ b， H（λ）＝ κ2，且 H 是从区间［b，λ］到区间［b，κ2］⊆［b，λ］的严格递增的映射.证毕.

定理 2.3 任取实数 λ、a、κ∈（0，1）使得

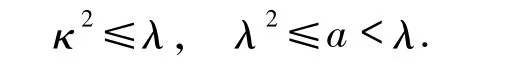
定义任意一个严格单调递减连续函数

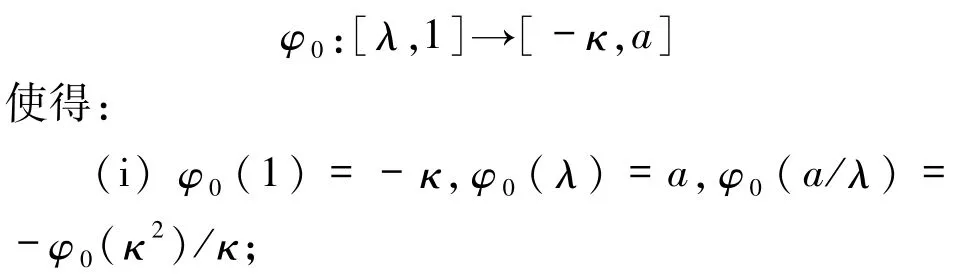
（ii）φ0（x）＝ -κx在［λ，1］上有唯一解 x＝1.则φ0能够被唯一延拓为方程（4）的严格单调递减的连续解.

证明 令

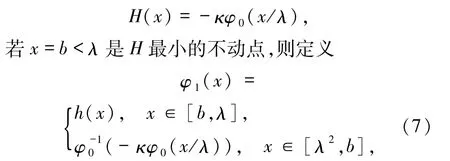
其中h为方程H的二次迭代根，即

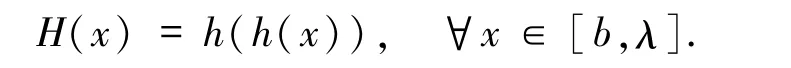
关于 H的二次迭代根，直接可以根据 Kuczma等［11-13］的方法得到.若 H 在［0，λ）上无不动点，则定义

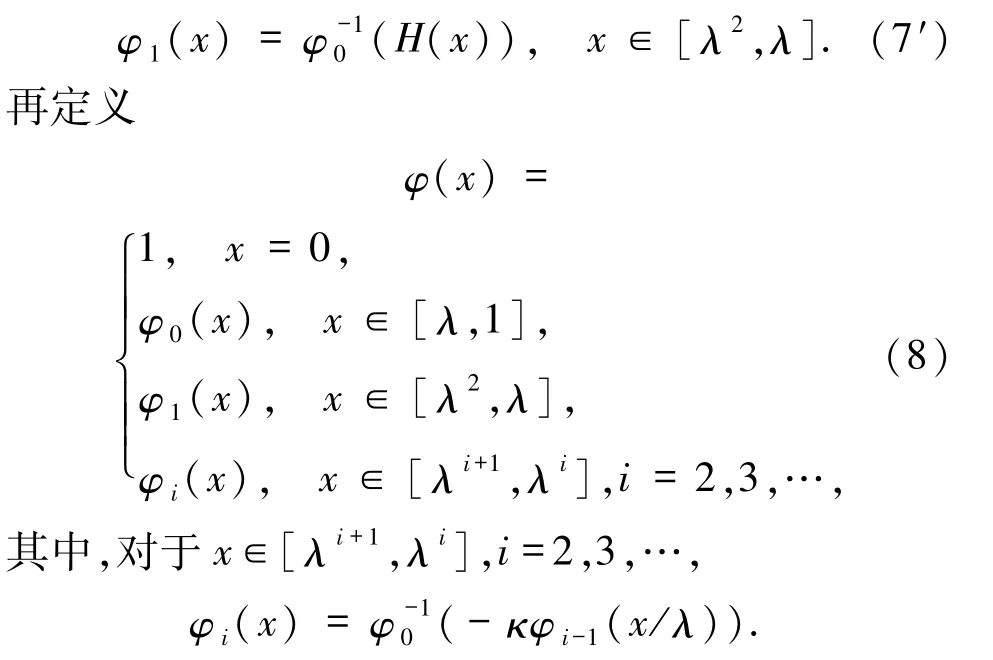
由类似于定理2.1的证明，φ是方程（4）的连续严格递减解.相反地，如果φi是方程（4）的严格单调递减解 φ 在区间［λi+1，λi］上的限制，则条件（i）、（ii）以及（7）或（7′）和（8）式均成立.证毕.