基于改进PSO算法的混合核SVM算法
2018-11-06徐中宇苏明玉姚庆安
徐中宇, 苏明玉, 姚庆安
(长春工业大学 计算机科学与工程学院, 长春 130012)
支持向量机(support vector machine, SVM)[1-2]是一种能在极其有限的信息条件下学习到最优预测结果的算法, 如何确定函数中相关参数对于增强混合核SVM的预测准确率非常重要[3-5]. 粒子群优化(particle swarm optimization, PSO)算法[6-7]是一种基于种群的全局并行优化方法, 具有收敛速度快并易于实现等优点. 本文通过PSO算法对混合核SVM[8]的参数进行寻优. 由于普通粒子群算法在进行优化选择时具有收敛慢和易陷入局部极小值等缺点, 因此目前已有多种改进粒子群优化算法[9-11]. 本文在粒子群算法的基础上通过改进并限制其速度和搜索范围等参数, 得到了性能更好的改进限制范围粒子群优化(improved limit particle swarm optimization, ILPSO)算法. 结果表明, 该算法能更好地提高粒子的搜索性能, 提升了粒子群的收敛速率, 达到了最优的效果及精确优化混合核SVM参数的目的.
1 方法描述
1.1 混合核函数的SVM分类模型
SVM能对非线性特征进行线性分析[12], 并在该高维空间内建立一个具有最大类间隔[13]的分类超平面, 即最优超平面. 使用混合核函数[14-15]取代单核, 不仅具有两个单核模型的优势, 而且有更佳的学习和泛化等能力. 基于单核的优势把多项式核和径向基核进行线性组合[16], 构造混合核函数Knew为
Knew=λ1Kpoly+λ2Krbf,
(1)
其中:
λi(i=1,2)为权重系数, 满足λ1,λ2∈(0,1), 且λ1+λ2=1.
1.2 改进的PSO算法
1.2.1 基本粒子群优化算法 PSO算法用于优化非线性函数, 设粒子群中第i个粒子在空间的位置为Xi, 其相应粒子速度为Vi, 此时局部极值为pbesti, 全局极值为gbesti. 在每次的粒子迭代中, 粒子从一个位置迭代到另一个位置, 每个粒子位置Xi根据不同因素的规则移动, 公式如下:
其中Vi为第i个粒子的速度, 定义为

其中:wmax,wmin分别为初始和最终的权重因子; itermax为最大迭代次数; iter为当前迭代数.
1.2.2 ILPSO算法设计 在PSO算法的实现中, 参数wi0,wi1,wi2,rnd1和rnd2都是该算法收敛的重要影响因子. 虽然普通的PSO算法有较快的收敛速度, 但在后期收敛速度较缓慢. 为使PSO算法加快收敛速度并提高求解质量, 本文通过以下3种策略对PSO算法进行改进.
1) 粒子速度限制.
初始化粒子随机位置在其限制范围内, 定义为
(2)
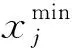
(3)
其中:
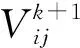
2) 减少搜索空间.
减少搜索空间有利于加快收敛速度. 在这种情况下, 搜索空间是动态调整的, 以达到预期的范围内. 首先, 在粒子i中对控制变量j搜索限制的最小和最大控制变量为
(4)
迭代(k+1)次, 搜索空间限制为
(5)
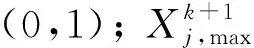
(6)
其中:Xij,min为粒子的最小位置;Xij,max为粒子的最大位置.
3) 交叉算子.

(7)
且
(8)
其中: randij为一个在[0,1]内的随机数;CR为交叉概率, 经验确定的最佳值为0.5.
2 基于ILPSO算法的混合核SVM参数优化
本文的混合核SVM需要提前给定的参数分别为正则化参数C、 相应核参数中的σ及不敏感损失函数参数ε. 通常选取合适的C值有利于避免由误差而引起的泛化能力减弱;ε用于控制拟合的管道, 有利于避免训练样本脱离管道壁;σ帮助SVM调解输入参数的敏感程度. 因此, 必须为混合核SVM选择最优的参数[16]. ILPSO算法优化参数的适应值可采用能直接反应SVM性能的均方差函数:
(9)
其中:fi为预测值;yi为实际值;m为样本个数. 改进的限制性粒子群优化算法对多核SVM的参数选择流程如图1所示.
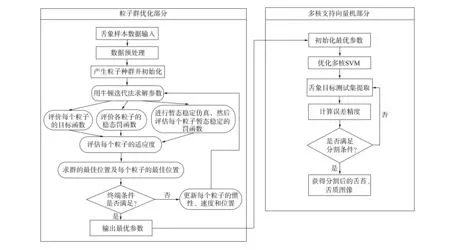
图1 基于ILPSO对混合核SVM参数寻优的流程Fig.1 Flow chart for optimization of hybrid kernel SVM parameters based on ILPSO
ILPSO算法描述如下.
输入: 粒子的维数和个数;
输出: SVM最佳参数组合(C,σ,ε,λ).

2) 用牛顿迭代法求解各个参数, 通过评价各个粒子的目标函数、 稳态罚函数及进行暂态稳定仿真, 评估每个粒子的暂态稳定的罚函数, 并对粒子的当前参数值进行评价.
3) 计算每个粒子的适应度. 重新定位粒子的最新位置为极值ibesti.
4) 重新确定粒子的初始速度和位置, 根据式(9)确定为新的适应度值Ffitness, 令ipresenti=Ffitness.
5) 比较更新后的ipresenti和全局最优位置gbesti. 若ipresenti>gbesti, 则gbesti=ipresenti.
6) 判断当前是否完全符合迭代终止的要求, 若符合, 则停止迭代, 并输出最适合的SVM参数组合; 若不符合, 则重新计算粒子的权重、 位置和速度, 并转2) . 若得到的最优解为多组时, 则取wi最小的一组.
7) 获得优化后的多核权重参数后, 开始优化多核函数, 并应用于舌象的舌苔、 舌质分割测试集提取中.
8) 计算误差精度, 并判断是否符合分割条件, 如果不符合, 则转7), 直至分割成功为止.
3 实验结果与分析
选用山西医科大学第一医院生物图像数据库中的100例舌象样本作为实验样本, 其中80例为训练样本, 20例为测试样本. 实验环境为CPU主频2.8 GHz, 内存8 GB的计算机, MATLAB 7.10平台.
将实验数据中的测试样本输入到构造的SVM中进行性能测试, 以计算得到的均方根误差函数值Frmse作为预测精度的参考值:
(10)
其中:xi为训练样本;yi为xi训练样本下的目标值;n为当前实验中的样本数量;C,σ,ε,λ为输入参数.
3.1 不同方法优化混合核SVM的性能比较
为比较不同优化算法对参数优化的效果, 本文实验中分别运用了十折交叉验证法、 PSO算法、 CPSO算法和ILPSO算法对混合核SVM参数求最优解, 经过100次实验, 分别用不同的优化方法对混合核SVM参数(C,σ,λ)进行优选, 其中λ,C和σ分别在[0,1],[0.01,1.1]和[1,1 000]内取值, 所得比较结果列于表1. 由表1可见, 相对于其他几种优化方法, 改进后PSO算法的平均测试误差和平均预测误差均有所降低, 达到了理想的实验结果.

表1 不同方法优化参数性能比较
3.2 舌苔、 舌质分割的SVM预测模型比较
本文实验通过不同的PSO算法对混合核SVM参数优化结果进行对比, 从而验证改进的PSO算法对舌苔、 舌质的分割具有较好的性能.
实验中的测试样本如图2所示. 通过改进的PSO(improved limit PSO)多核SVM算法(ILPSO-SVM)、 ILPSO单核SVM算法(ILPSO-SVM)、 一般的PSO(normal PSO)多核SVM算法(NPSO-SVM)、 一般的PSO单核SVM算法(NPSO-SVM)、 遗传算法(GA)多核SVM算法(GA-SVM)和普通的SVM算法对舌象的舌苔、 舌质分类进行仿真实验, 实验结果列于表2. 由表2可见, 遗传算法的种群规模与ILPSO算法相同, 交叉概率为0.8, 变异概率为0.037, 代沟为0.9. 在分割实验中, 本文的ILPSO-SVM多核和单核分割舌苔、 舌质结果如图3所示.
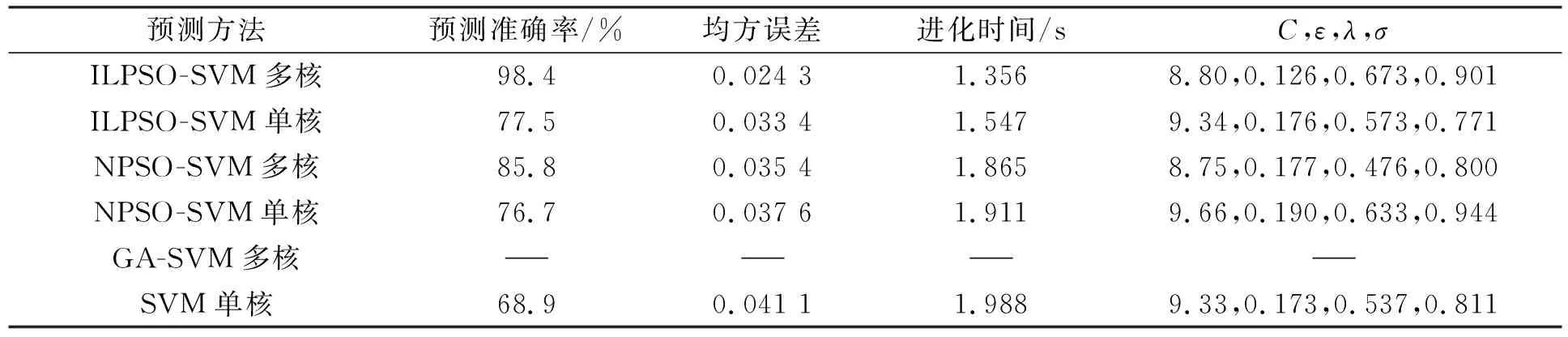
表2 各种预测方法仿真结果对比
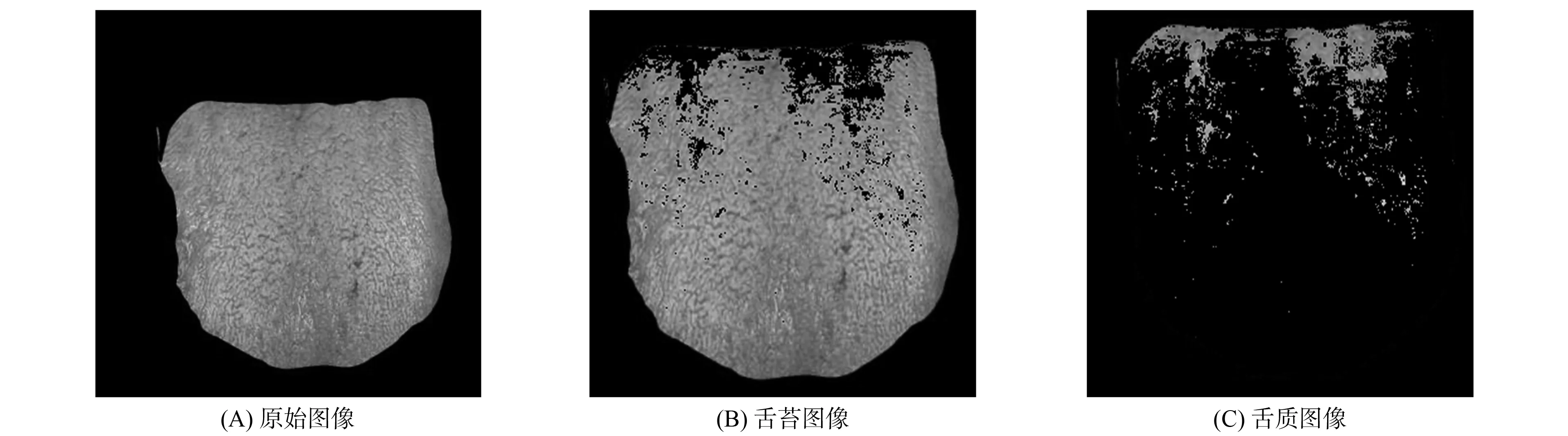
图2 基于粒子群的混合核SVM舌象分割图像样本Fig.2 Hybrid kernel SVM tongue image segmentation image sample based on particle swarm

图3 ILPSO算法的多种核SVM舌象分割图像Fig.3 Multiple kernel SVM tongue image segmentation images of ILPSO algorithm
由图2和图3可见, ILPSO-SVM多核和单核分割的舌苔和舌质差别较大, 且多核的分割效果更接近于标准结果. 由表2可见, 本文改进的PSO优化多核SVM所生成的预测模型在很大程度上逼近于理想模型, 不仅能获得较精确的全局最优解, 且具备较高的寻优效率(较短的进化时间); 遗传算法(GA)由于进行速度无法满足要求, 最终收敛到局部极小值, 寻优失败. 相比其他预测方法, 本文算法的预测准确度有所提升, 且误差率明显降低.
综上所述, 本文算法较好地结合了单核模型的优势, 运用组合的方式生成多核SVM模型, 并通过改进的PSO算法进行参数选择, 克服了人工选取参数的主观性. 实验结果表明, 在舌象中的舌苔和舌质颜色交错融合的特性中, 通过本文算法可得到更逼近理想的分割效果, 相比其他优化算法, 优化的核参数对于舌苔和舌质的分割有更高的分割精度和泛化性能.
