分布式离散事件系统的安全可诊断性算法
2018-11-06欧阳丹彤罗知雨耿雪娜张立明
欧阳丹彤, 罗知雨, 耿雪娜, 张立明
(1. 吉林大学 计算机科学与技术学院, 符号计算与知识工程教育部重点实验室, 长春 130012; 2. 长春理工大学 计算机科学与技术学院, 长春 130022)
基于模型诊断(model-based diagnosis, MBD)方法具有设备独立性、 易更新和维护等特点, 因此已逐渐成为故障诊断领域的核心方法, 很多领域都使用该方法进行系统诊断[1], 而且MBD问题可以转换为可满足性(SAT)[2-3]问题, 或使用文献[4]的方法进行求解. 文献[4]给出了可诊断性的充要条件. 在MBD中, 模型是否正确影响诊断的效果及效率, 不同模型条件下的可诊断性主要针对不同系统下的可诊断性问题. 常见的系统模型有离散事件系统(discrete event systems, DES)[5]、 模糊DES[4]及分布式DES[6]等. 由于系统的复杂性逐渐增加, 模型的规模也逐渐增加, 为了降低模型规模及复杂系统的计算量, 人们提出了分布式系统. 在分布式系统中, 为了解决对大规模系统的全局模型进行可诊断性分析的困难, 全局模型被分割成多个有相同通信事件的局部模型或组件, 每个局部模型独立分析其可诊断性, 由于硬件原因, 局部可诊断性与全局可诊断性不一定相同, 因此分布式系统通过通信事件进行同步, 以获得全局模型的可诊断性. 一些经典的DES诊断方法同样在分布式系统诊断中使用, 如诊断器[4]、 同步[7]等方法. 同时, 对分布式系统的诊断方法进行了许多改进[8-10], 从而更快速、 更准确地判定系统的可诊断性.
尽管在故障发生一段时间后可诊断的系统才能检测到该故障发生, 但如果没有及时完成检测, 则发生的故障可能会危害系统本身及人身财产安全. 为了避免安全事件的发生, 人们希望在系统执行被禁止事件序列前检测到故障的发生, 基于此, Paoli等[11]提出了判定DES的安全可诊断性. 在文献[11]的基础上, 刘富春等[12-14]提出了判定模糊DES、 随机DES的安全可诊断性问题及对DES安全可诊断性的改进算法.
本文提出一种分布式DES的安全可诊断性算法. 对于给定的分布式系统及被禁止事件序列集合, 首先使用同步[4]的方法得到系统的全局模型, 然后判断系统对给定故障是否可诊断, 确定系统对给定故障可诊断后, 构建系统对给定故障及相应被禁止事件集合的安全诊断器来判断系统在故障发生后是否发生被禁止事件序列, 假设未发生故障或故障发生后未发生被禁止事件序列, 则系统是可诊断的且是安全可诊断的, 否则系统不是安全可诊断的.
1 预备知识
1.1 分布式离散事件系统及其可诊断性

图1 由3个局部模型构成的系统S1Fig.1 System S1 composed of three local models
定义1(局部模型)[6]第i个局部模型Γi定义为一个有限状态自动机Γi=(Qi,Ei,Ti,q0i), 其中:Qi为有限状态的集合;Ei为事件的集合, 包含3个互不相交的集合, 分别为故障事件集合Fi、 可观测事件集合Oi和通信事件集合Ci;Ei,Oi,Fi只发生在Γi中;Ti为转移函数集合,Ti⊆Qi×Ei×Qi;q0i为系统的初始状态.

其中:ψ表示同步事件集合且ε∉ψ;ev(ti)表示ti的事件标签.
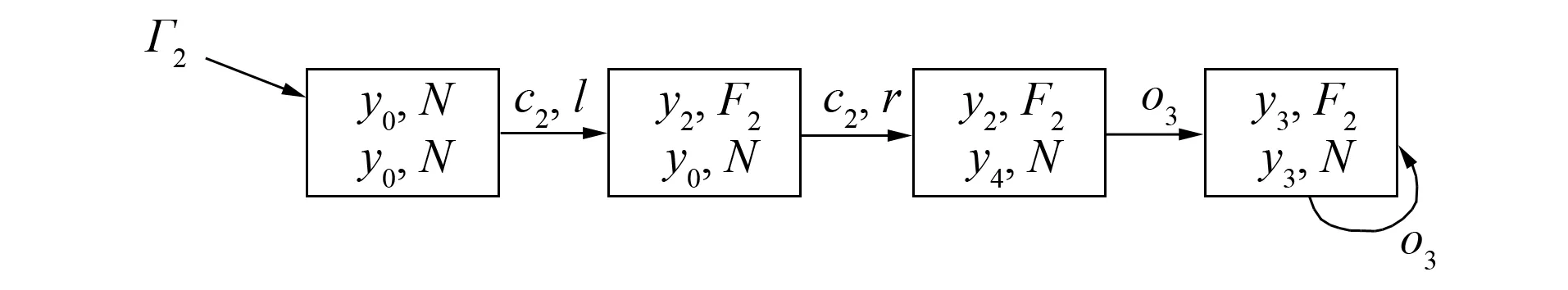
图2 局部模型Γ2自同步得到的系统GFig.2 System G obtained by self-synchronizing local model Γ2
图2为图1中Γ2的诊断器以可观测事件为同步事件, 自同步得到系统G. 系统内不同的局部模型间通过两个局部模型间相同的通信事件进行同步转换, 可得到系统的全局模型. 假设系统由n(n≥1)个局部模型组成, 则系统{Γ1,Γ2,…,Γn}的全局模型定义如下.
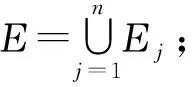
Cj为通信事件.
定义3(局部可诊断性)[6]若局部模型Γ中发生故障fi后又发生了有限个可观测事件, 则fi在该局部模型中是可诊断的, 即fi是局部可诊断的, 即
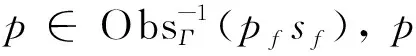
其中:pf表示以初始状态p0为起点, 以fi发生后的状态为终点的路径;sf表示pf的后续路径; Obs表示可观测投影的映射函数; Obs-1表示可观测投影的逆映射函数[2].
由文献[6]知, 如果fi是局部可诊断的, 则fi是全局可诊断的.
1.2 离散事件系统的安全可诊断性
系统中可以发生多类故障事件, 每类故障事件包含多个故障事件, 假设对于第i类型故障fi的被禁止事件序列集合为Φi,Φi∈E*, 其中E*为E的闭包[2]. 为了满足安全性, 在某类故障fi发生后, 避免系统执行Φi.
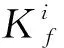
其中[s∈Ψ(Efi)](i=1,2,…,m)}([v∈Φi,v为u的子序列]),
其中:Ψ(Efi)表示以第i类故障事件结尾的路径;L/s表示语言L中发生在事件s的后续路径.
如果一个系统是安全可诊断的, 则该系统首先是可诊断的.
定义5(可诊断性)[4]语言L可诊断的条件如下:
(∀i∈Πf)(∃ni∈)(∀s∈Ψ(Efi))(∀t∈L/s)(‖t‖≥ni⟹D),
其中D为ω∈Obs-1[Obs(st)]⟹Efi∈ω.
定义6(Fi确定与不确定性)[4]若诊断器中存在状态q, ∀(x,l)∈q满足Fi∈l, 则称q是Fi确定的. 反之, 若诊断器中存在状态q,∃(x,l),(y,l′)∈q且Fi∈l,Fi∉l′, 则称q是Fi不确定的.
定义7(安全可诊断)[11]语言L安全可诊断的条件如下:
1) 可诊断性条件同定义5;
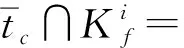
2 安全诊断器的构造

定义8(非法语言标签)[11]非法语言的标签函数为
其中:Bi表示故障发生后又执行了相应的被禁止事件串;S表示无故障事件发生或故障事件发生后未执行相应的被禁止事件.
通过非法语言的标签函数能构造系统的非法语言识别器.
定义9(非法语言识别器) 对系统Γi中发生的故障fi及对应的被禁止事件集合Φi构造的非法语言识别器Gr为有限状态自动机Gr={Qr,E,Tr,q0r}, 其中:Qr为状态空间,
Qr∈Q×πl(s),πl(s)=π(s)×l(s),
l(s)为故障标签,
q0r=(ε,N-S);Tr:Qr×E×Qr为状态转换函数,
Tr((s,πl(s)),σ)=(t,πl(t)),s,t∈Qr,σ∈E,
转换规则为
通过非法语言识别器可获得添加安全标签的自动机:
Γm=Γi×G1×…×Gm=(Qm,E,Tm,q0m),
其中Γm中的一个状态
z=[q,(s1,π(s1)),…,(sm,π(sm))].
图3为G对f2,{o3}构造的非法语言识别器Gr.
定义10(安全诊断器) 若存在自动机γ=(Q,E,T,q0), 则该自动机对fi和Φi的安全诊断器为
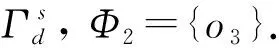

图3 非法语言识别器GrFig.3 Illegal language recognizer Gr

图4 安全诊断器

1)q为Fi不确定状态;
2)q,q′状态如下:
①q为Fi确定状态;
②q′为Fi不确定状态.
因图4中存在F2不确定状态[(y3,F2-B2),(y3,N-S)], 因此由定理1知该系统不是安全可诊断的.
3 分布式离散事件系统判定安全可诊断算法
3.1 分布式离散事件系统的安全可诊断性
判断系统是否安全可诊断前, 首先需将局部模型通过同步操作构成系统的全局模型, 根据定义2, 可由下列算法构建系统的全局模型.
算法1构建全局模型算法.
Function: GS( );
Input: 局部模型{Γ1,Γ2,…,Γn};
Output:Γ;
if 系统安全可诊断, return系统可诊断;
if系统不可诊断, return 系统不可诊断;
Begin
1) Initialization:A←{Γ1,Γ2,…,Γn}{Γi};
2) whileA≠Ø do
3) 从A取出与Γ1有相同通信事件Ci的Γi;
4)Γi←Synch(Γi,Γj,Sync(ti,tj),Ci);
5) end while
6) AbstractKeyPath(Γi);
7)Γ←Γi;
8) DR(Γ);
9) Check1(Γ);
End.
算法1中步骤4)使用函数Synch(Γi,Γj,Sync(ti,tj))先将两个局部模型同步获得一个新的模型, 再将结果保存在Γi中; 步骤6)中AbstractKeyPath(Γi)为对系统剪枝保留关键路径, 即只保留包含故障的语言及可诊断性与其相同的语言; 步骤8)中DR(Γ)为构建诊断器; 步骤9)中Check1(Γ)为检查系统是否安全可诊断, Check1( )可能有两种结果:
1) 若系统包含Fi不确定状态环, 则返回系统不可诊断;
2) 若系统不包含Fi不确定状态环, 则返回系统可诊断.
若系统可诊断, 则根据定义8和定理1构建系统的安全诊断器, 用以判断系统是否安全可诊断.
算法2安全可诊断性判断算法.
Function: SDR( );
Inputs:Γ;
故障事件fi;
被禁止事件集合Φi;
Outputs: if 系统安全可诊断, return系统安全可诊断;
if 系统不可安全诊断, return系统不可安全诊断;
Begin
1) Lable(Γ);
2) DeleteUnobEvents(Γ);
3) Check(Γ);
End.
算法2中步骤1)函数Lable(Γ)为使用前状态与相应事件, 根据定义9计算非法语言标签; 步骤2)中函数DeleteUnobEvents(Γ)为删除系统中的不可观察事件, 只保留可观测路径; 步骤3)中函数Check( )为检查系统是否安全可诊断, Check( )可能有两种结果:
1) 若系统不满足定理1, 则返回系统不可安全诊断;
2) 若系统满足定理1, 则返回系统安全可诊断.
3.2 复杂性分析
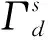
设全局系统最大状态数量为
(|Q1|×|Q2|×…×|Qm|×…×|Qn|),
最大转换数量为
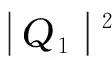

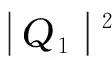
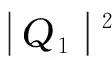
4 实验及实例分析
4.1 实 验
实验采用的测试环境为: Dell Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz, Windows 64位系统, 8 GB内存, 920 GB硬盘, eclipse编译器.


图5 系统模型S2Fig.5 Model of system S2

图6 系统模型S3Fig.6 Model of system S3


表1 诊断前后状态数对比
4.2 实例分析
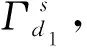

图7 全局模型G1Fig.7 Global model G1
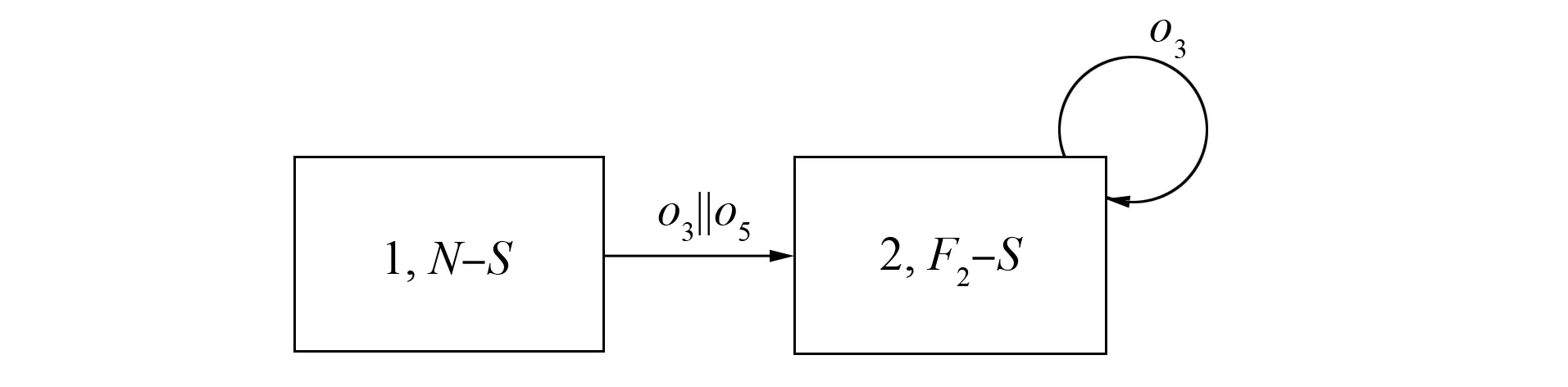
图8 安全诊断器
综上所述, 本文提出了一种分布式DES安全可诊断性的判断算法, 通过使用非法语言识别器, 添加安全标签获得安全诊断器, 从而得到诊断结果. 实验结果表明: 用该算法进行安全可诊断性判断的时间在可接受范围内; 在空间上, 最好的实例状态数缩减到7倍, 平均状态数缩减了5.45倍.
