一种薄壁件柔性多点加工工装布局优化技术

陈禹至，陈蔚芳，施圣杰

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

飞机大型薄壁件轮廓尺寸大、刚度低、精度要求高、加工工艺性差。在切削力、装夹力等作用下极易产生加工变形[1]。近年来，随着自动化水平的不断提高，研制数字化支撑单元多点柔性工装系统能够有效地解决大型薄壁件在铣削加工中的变形问题。其中比较完善的有西班牙MTorres 公司研发的TORRESTOOL 柔性工装系统和美国CAN 制造系统公司研发的基于POGO 柱单元的柔性工装系统，已被多家航空制造企业应用到生产中[2-4]。

传统的装夹方案确定依赖于直观判断和经验积累，或者有针对性地对工件弱刚度部位进行加固。其缺陷主要在于：弱刚度部位的针对性加固需长时间地尝试和调整。为此，大量研究围绕着工件装夹定位布局的优化展开。张晓峰、冯婷等[5-6]通过有限元方法对薄壁件多点柔性加工变形进行分析，并总结相关变形规律；陆俊百等[7-8]提出了自适应优化的方法和遗传算法两种方法优化装夹布局，经过优化分析得到了最优布局；王少峰等[9]提出了基于变形敏感度的思路通过改善工艺系统刚度进行布局优化，可以有效抑制加工变形。

本文在以上研究的基础上，利用有限元计算和迭代算法，提出了一种快速满足加工要求的工装布局优化方法。该方法为多点柔性工装高效合理地选用支撑单元布局以控制薄壁件加工变形提供了有效途径。

1 多支承/定位点布局优化模型

1.1 多点支承/定位阵列工装的数学简化

本文的模块化柔性工装采用自行设计的独立十字滑台结构如图1所示，每个定位/支承具有3个方向的自由度，这在一定程度上提高了工装的柔性。与大型滑枕滑座结构的柔性支承通用模型图2(a)不同，独立十字滑台型柔性工装系统的通用模型可简化为图2(b)所示。

图1 独立十字滑台型柔性工装系统结构

图2 两种柔性工装简化图

假设柔性工装由k个柔性柱组成，柔性柱分布在底板上，分布位置可根据工件形状、工作空间等具体情况布置，则工装的支承/定位阵列可用数学表示为：

P=P(P1，P2,…Pk) (i=1,2,…,k)

(1)

1.2 优化模型

多支承/定位点布局优化方法的研究关键在于：找出1个合适的多点支承/定位布局P，在满足所有约束时，使工件加工载荷下的工件加工变形最小。

1) 构建目标函数

将加工轨迹离散成n个点，以加工轨迹上最大加工变形最小为目标，数学描述为：

Min[max(|δ1|,|δ2|,…,|δk|,…,|δn|)] =f(P)

(2)

式中：δk为加工路径上第k个点的变形量。

2) 构建约束条件

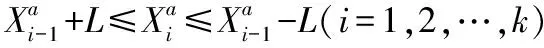
(3)

(4)

式中i为每行的柔性柱数目。

(5)

(6)

(7)

而在优化过程中，主要根据绝对坐标计算，在确定各柱的绝对坐标后根据基准坐标即可计算出各方向的相对坐标，从而控制各轴动作。

2 工装布局快速优化算法

在优化过程中为简化计算量，近似认为最靠近刀具作用点的支撑对工件在作用点处的变形影响最大。优化过程实现的具体步骤如下:

1) 根据实际情况安装十字滑台并将柔性柱3个方向分别回零，确定优化初始布局；

2) 构造工件的有限元模型，并根据布局定义约束条件；

3) 将刀位轨迹离散成点，分别计算切削力加载在轨迹上各点处的最大变形，取出1次走刀过程中的最大变形值及其位置坐标，并计算出距离最大变形处最近的支撑点位置坐标；

4) 将支撑点沿x方向向靠近刀位轨迹方向移动1个特定距离，再次计算改变支撑位置后的最大变形，返回至步骤2)；

5) 当步骤3) 出现沿x方向的震荡时，说明仅仅沿移动x方向并不能取得想要的效果，此时开始移动y方向。过程与步骤3) 一致，直到出现在y方向的震荡，此时返回至步骤3) 继续调整x方向；

6) 判断结果是否满足允许的最大变形要求，若满足则退出优化，表示优化完成；若不满足要求，继续优化，若循环次数超过最大设置时，强制退出，此时优化失败。

上述多点支承/定位布局优化流程如图3所示。

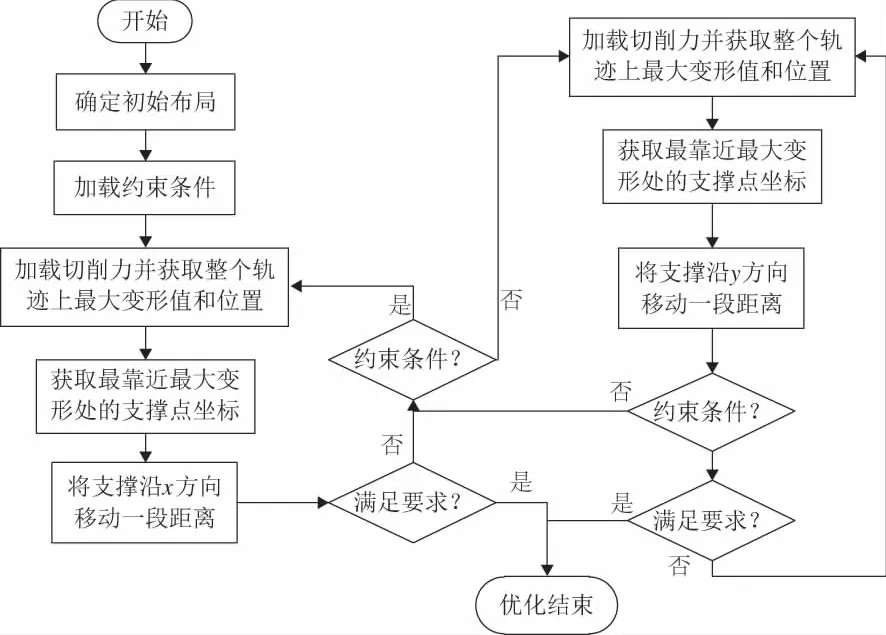
图3 多点支承/定位布局优化流程

3 实例计算

为了验证本文方法的实际效果，实例中薄壁件选用7050-T7451铝合金，尺寸为1 200 mm×800 mm，厚度为3 mm,其弹性模量为70.3 GPa，泊松比为0.33。多点支承/定位初始布局坐标见表1。

一般薄壁件铣削切边等加工路径多为直线或折线，本实例中以典型的折线加工轨迹为例，将加工轨迹离散成58个点，每2个点之间相隔20mm，切削路径离散点坐标如表2所示，初始布局与加工轨迹如图4所示。沿工件加工路径依次施加350N法向加工载荷分量，将走刀轨迹上最大变形设置在工艺要求0.7mm内，按照前面所述算法进行布局优化。

表1 多点支承/定位初始布局坐标

表2 切削路径离散点坐标

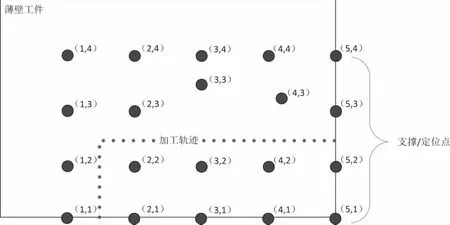
图4 初始布局与切削路径

首先，程序计算在现有约束条件下刀轨各离散点的变形值，此时最大变形出现在支撑点(2,1)附近，因此将支撑点(2,1)沿x轴负方向移动一段固定距离(20mm)，再根据新的约束条件计算变形值，此时仍然是(2,1)附近变形较大，因此继续移动(2,1)，再次计算，此时最大变形位置转移至(5,3)附近，将(5,3)沿x负方向移动固定距离，继续计算。当循环一定次数后点(5,3)会出现沿x轴的震荡，此时程序转入调整y方向继续优化。当y方向也出现震荡时，程序返回调整x方向，直到满足优化目标后退出。在优化过程中不断检测支撑点是否满足行程条件。

最终经过18次循环优化，优化后走刀轨迹上最大变形为0.679mm，对比优化前最大变形1.685mm减小了59%，如图5所示。优化前后支撑点的位置如图6所示，优化后加工路径附近的支撑点分布密度变大，这在一定程度上提高了工件的刚度。

4 结语

本文结合薄壁件加工过程中多支承/定位布局优化这一基础理论问题，提出了一种以最小化最大加工变形为目标函数的薄壁件加工布局优化方法，并通过不断调整最大变形处附近最近点的支撑位置来实现。以常见的大型薄壁件为实例进行分析，对优化前后的工件加工轨迹变形计算结果进行了比对，发现最大加工变形被控制在0.679mm，相对优化前的1.685mm减小了59%，由此验证了该优化方法的正确性和合理性，为实际生产中多支承/定位点布局的快速优化提供了指导。

图5 优化前后走刀轨迹加工变形对比

图6 优化前后支撑点位置图