钛合金波纹夹芯结构高应变速率下压缩行为研究
2018-11-05王文涛陶杰
王文涛, 陶杰
(1. 南京航空航天大学 材料科学与技术学院,江苏 南京210016; 2. 江苏先进无机功能复合材料协同创新中心,江苏 南京 210016)
0 引言
波纹夹芯结构无论服役于航空航天领域还是舰船火车领域,都不可避免要承受冲击载荷。相比于静态载荷下的力学性能,波纹夹芯结构在动态载荷下可能有应力波、惯性和应变率效应,因而表现出和静态载荷下不一样的性能。波纹夹芯结构承受的动态载荷可以分为高应变速率冲击和低速冲击,高应变速率冲击主要的试验手段是霍普金森压杆试验和爆炸冲击试验。
霍普金森压杆试验作为1种比较常用的测试材料动态力学性能的方法,目前应用在泡沫夹芯结构中最多,尤其是泡沫铝。研究的重点集中在泡沫铝结构应变率效应是否明显以及泡沫铝的相关参数对其吸能性能的影响[1-2]。霍普金森压杆在蜂窝夹芯结构上同样有较多的应用[3-4],但结果发现蜂窝结构的应变率效应同样存在争议。通过霍普金森压杆试验研究波纹夹芯结构的应变率效应目前鲜有报道。Klçaslan等[5-6]利用霍普金森压杆试验对单层和双层铝合金梯形波纹夹芯结构的动态力学性能进行了研究,结果表明结构的屈曲应力随着应变速率的提高而增加,作者将其归因于微惯性效应改变了结构的屈曲模式,并通过有限元模拟发现三角形波纹夹芯具有更高的微惯性效应。然而对于钛合金波纹夹芯结构,尤其是多层多取向排列的波纹夹芯结构的高速冲击性能,目前研究甚少。
考虑到钛合金波纹夹芯结构在空间飞行器上的服役环境中可能受到动态冲击载荷的作用,如空间碎片撞击航天器,强烈气流对飞行器的冲击,导弹攻击航天器目标等,而材料在准静态载荷和动态载荷作用下的力学性能存在着显著的差异。因此研究其动态力学性能及相关机理,对该类波纹夹芯结构的设计与开发以及工程应用等方面具有重要意义。
1 材料和试验方法
1.1 材料和试样制备
波纹夹芯层材质为0.3 mm厚的TA2工业纯钛,面板材料为1 mm厚的Ti-6Al-4V,面板和夹芯层之间通过钎焊连接在一起,夹芯层的详细几何参数如图1(b)所示,试样直径32 mm。试样分为5种,分别命名为MD、MD/MD、 MD/CD、MD/MD/MD 和MD/CD/MD如图2(a)所示。MD和CD方向的定义如图2(b)所示。
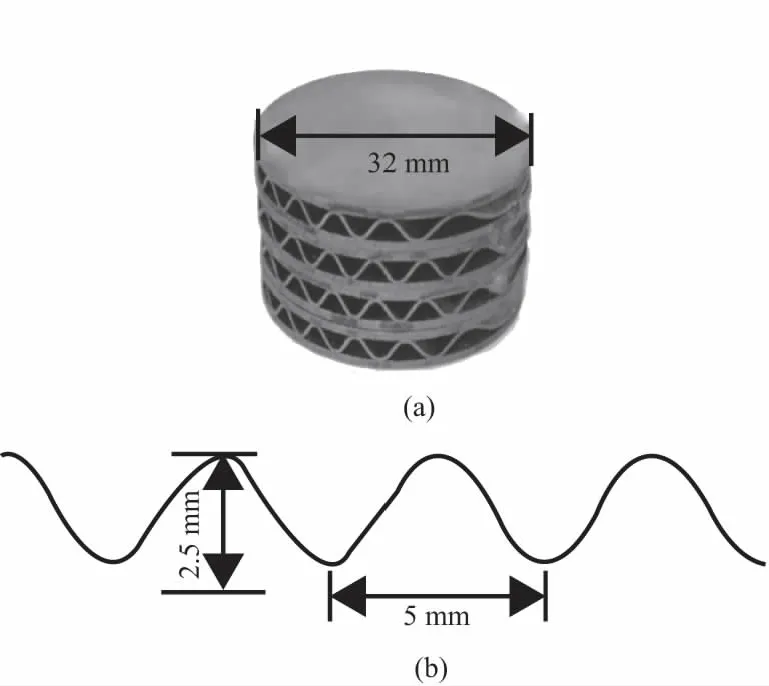
图1 试样及夹芯层几何尺寸

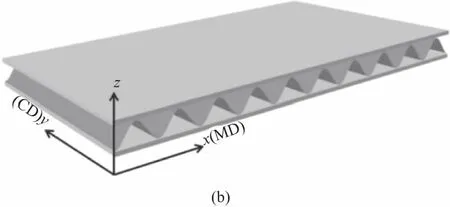
图2 试样类型及MD、CD方向定义
1.2 试验方法与参数
SHPB实验装置主要有子弹、入射杆和透射杆组成,如图3所示。当子弹以一定的速度沿轴向撞击入射杆时,在入射杆中产生一压缩应力脉冲εi,试样在该脉冲作用下高速变形,与此同时将反射1个脉冲εr回到入射杆中,并经过试样透射1个脉冲εt进入到透射杆中。压杆中的脉冲信号通过应变计来测量,入射杆表面的应变计测量入射和反射信号εi和εr,透射杆表面的应变计测量透射信号εt。
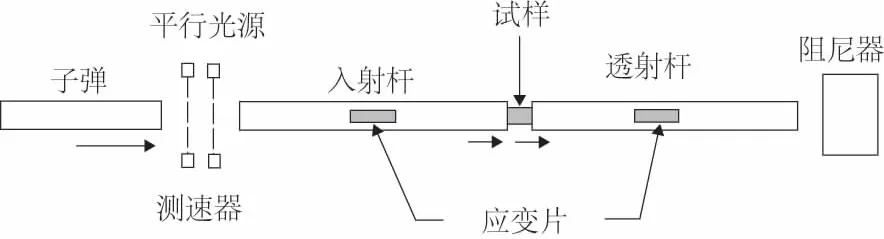
图3 霍普金森压杆示意图
霍普金森实验装置中的压杆(包括入射杆和透射杆)材料为LC4铝合金,直径37 mm,波速C0为4 500m/s,弹性模量72GPa,子弹长度600mm。为减少试件端部与入射杆、透射杆之间的摩擦,在试件的两个端面接触处涂抹含二硫化钼的润滑油。实验通过调节高压气瓶释放气压值来控制撞击杆的冲击速度,从而实现不同的应变速率。本文所选的气压值分别为0.1MPa、0.15MPa、0.25MPa和0.4MPa,共对应4种冲击速度,每种冲击速度下共做3组重复试验。
2 试验结果与讨论
2.1 压缩应力-应变曲线
5种波纹夹芯结构在高应变速率下及准静态下的应力-应变曲线(如图4所示)相似,尽管在高速变形下无法捕捉到其变形过程,但是推断其变形过程应有类似之处。从应力-应变曲线上还可以发现不仅峰值应力与应变速率之间呈正相关关系,即便在峰值应力之后,应力水平仍随着应变速率的增加而提升,这说明波纹夹芯结构在其塑性变形阶段,即主要的吸能阶段,具有明显应变率效应。目前对波纹夹芯结构应变率效应的研究比较少,主要集中在泡沫铝及蜂窝夹层结构,波纹夹芯结构的应变率效应的原因主要有以下几点:局部变形、微惯性效应及密实化压缩。首先,对于波纹夹芯结构的夹芯层,由于其几何结构是正弦形,不同于蜂窝结构,从几何结构上来说正弦形在受压的时候必然存在一个或几个薄弱点。由于正弦形状的规则性,这些薄弱点位于同一个面上,在受到高速冲击时,变形会突然集中在薄弱面及其附近,造成局部迅速压实且应变速率远高于名义应变速率,应力水平也会很高。峰值应力的应变率效应可以由此解释。当然除了几何结构引起的局部变形之外,试样中存在的初始缺陷同样会引起局部化变形。其次,波纹夹芯结构的夹芯层壁板在变形过程中发生扭转、弯曲等会引起微惯性效应,以阻止夹芯层壁板的进一步发生塑性屈曲,而且应变速率越高,这种效应越明显,从而提高了应力水平。最后当波纹夹芯结构进入密实化阶段之后,应变速率越高,撞击的力越大,应力水平必然会提高。
2.2 本构方程
用于描述材料动态力学特性的本构模型大致可分为两类,即理论型和经验型本构模型,理论型模型最具代表性的有Perzyna提出的三维应力状态下的过应力弹粘塑性理论模型,这类模型虽有较好的理论和数学基础,但过应力与粘塑性应变率之间函数关系、内变量和内变量演化方程、自由能等参数的确定较繁锁,使其在实际应用中受到很大的限制,最常用的经验模型则有Johnson-Cook 本构方程[7]:
(1)
此外Perzyna也提出了1个经验模型[8]:
(2)
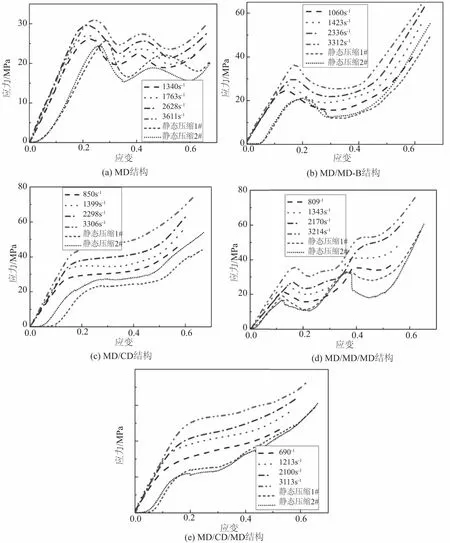
图4 钛合金波纹夹芯结构准静态及高应变速率下压缩应力-应变曲线
式(2)没考虑温度因素,但考虑了应变速率的影响,其中C和m是应变速率系数,σ0(ε)是静态条件下的应力。
Perzyna提出的经验模型在经典弹塑性理论的基础上给出的单轴率相关本构模型,这种模型避免了屈服面的概念,本构方程得到简化,在实际中得到了广泛的应用。考虑到5种结构的压缩应力-应变曲线并不都是单调的,而是有波动的,因而不满足Johnson-Cook 本构模型,所以本文将利用Perzyna经验模型研究波纹夹芯结构的应变率效应。
1) Perzyna经验模型
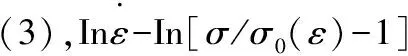
(3)
对于每1种波纹夹芯结构,分别取其4个不同应变速率下某一应变对应的应力值,对这4个点用最小二乘法作线性拟合,即可求得相应的m值和C值,每1个应变条件下都可以求得1组m值和C值,最终取不同应变下的平均值。以MD结构的压缩应力-应变曲线为例,求解其Perzyna经验本构模型。
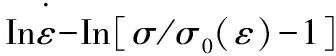
(4)
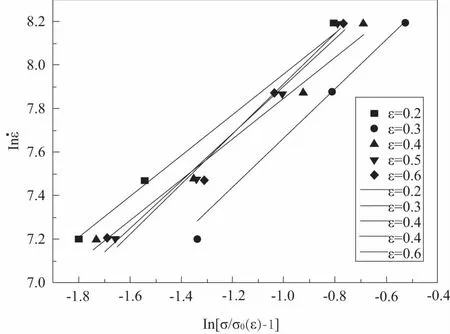
图5 MD结构高应变速率下关系曲线
同样的方法可以获得MD/MD、MD/CD、MD/MD/MD以及MD/CD/MD结构高应变速率下的Perzyna经验本构模型。
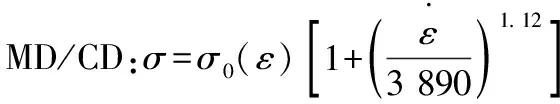
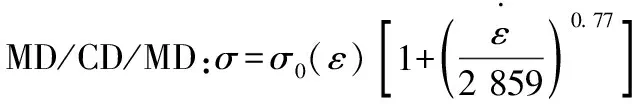
2) Perzyna经验模型误差比较
5种结构的m值和C值的标准差如表1所示,标准差能反映1个数据集的离散程度,但是由于各种结构的m值和C值并不相同,单纯比较他们之间的标准差并不合理,因此引入变异系数(C·V)(变异系数C·V=(标准差/平均值)× 100%),从而消除尺度不同的影响,实现客观比较。
从表1中可以看到MD/CD结构m值和C值的变异系数最小,表明其拟合线的斜率和截距值离散程度最小。MD/MD结构m值的变异系数超过了20%,C值的变异系数也达到了15.40%,在所有结构中离散程度最大,其次MD/MD/MD结构的m值和C值的变异系数均超过了15%,离散程度也较大。MD和MD/CD/MD结构m值和C值的变异系数均在10%左右,处于可以接受的离散程度范围之内。
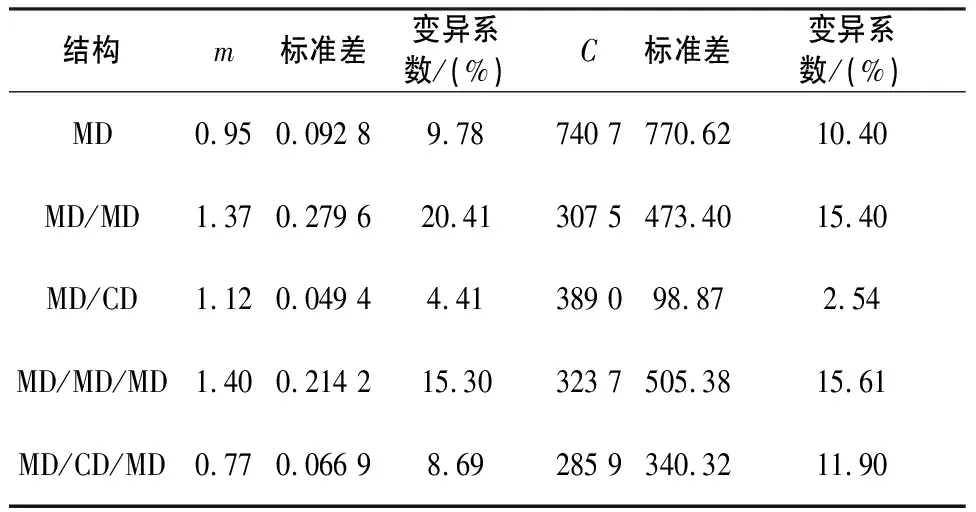
表1 5种结构Perzyna经验模型中m值和C值离散度
3) Perzyna经验模型验证
利用所建立的Perzyna本构模型可以计算出各种结构在每一个应变值下的应力值,在此选取建立模型时所用到的应变值,通过各种结构的本构模型计算出相应的应力,并与试验值相比较,如图6所示。可以发现,对于MD结构,应变<0.3范围内,试验值与预测值相差较大,而当应变超过0.4之后,试验值与预测值之间的吻合度较高。MD/MD结构在大应变及高应变速率下试验值和预测值差距明显。MD/CD结构则在所有应变及应变速率下试验值与预测值显示了高度的吻合性,这也说明所建立的Perzyna本构模型可以准确地描述MD/CD结构在高应变速率下的应力-应变行为及应变率效应。MD/CD/MD结构则在应变为0.25和0.4时试验值与预测值有较明显差距,在高应变速率下尤其如此。MD/CD/MD结构试验值与预测值之间的差距基本上保持一致。整体来看,大应变和高应变速率处的试验值与预测值之间最容易出现明显误差。
为了定量地评价本文所建立的本构方程的准确性,引入了相关系数r和平均相对误差AARE等2个标准统计学参数,其表达式如式(5)-式(6)所示。
(5)
(6)
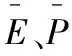
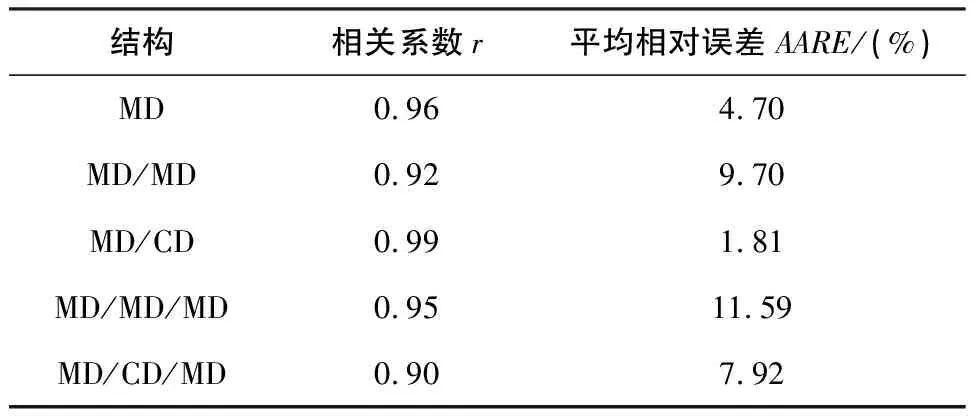
表2 试验值与预测值之间的相关系数和平均相对误差
3 结语
1) 在高应变速率下,单层MD结构、双层MD/MD、MD/CD结构和三层MD/MD/MD、MD/CD/MD结构都表现出了明显的应变率效应,即应力水平随应变速率增加而提高。
2) 5种波纹夹芯结构在高应变速率下应力-应变曲线的Perzyna经验模型精度不一,其中MD/CD结构的Perzyna经验模型精度最高,其次是MD/CD/MD和MD结构,夹芯层呈相同方向排列的多层波纹夹芯结构的Perzyna经验模型精度较差。
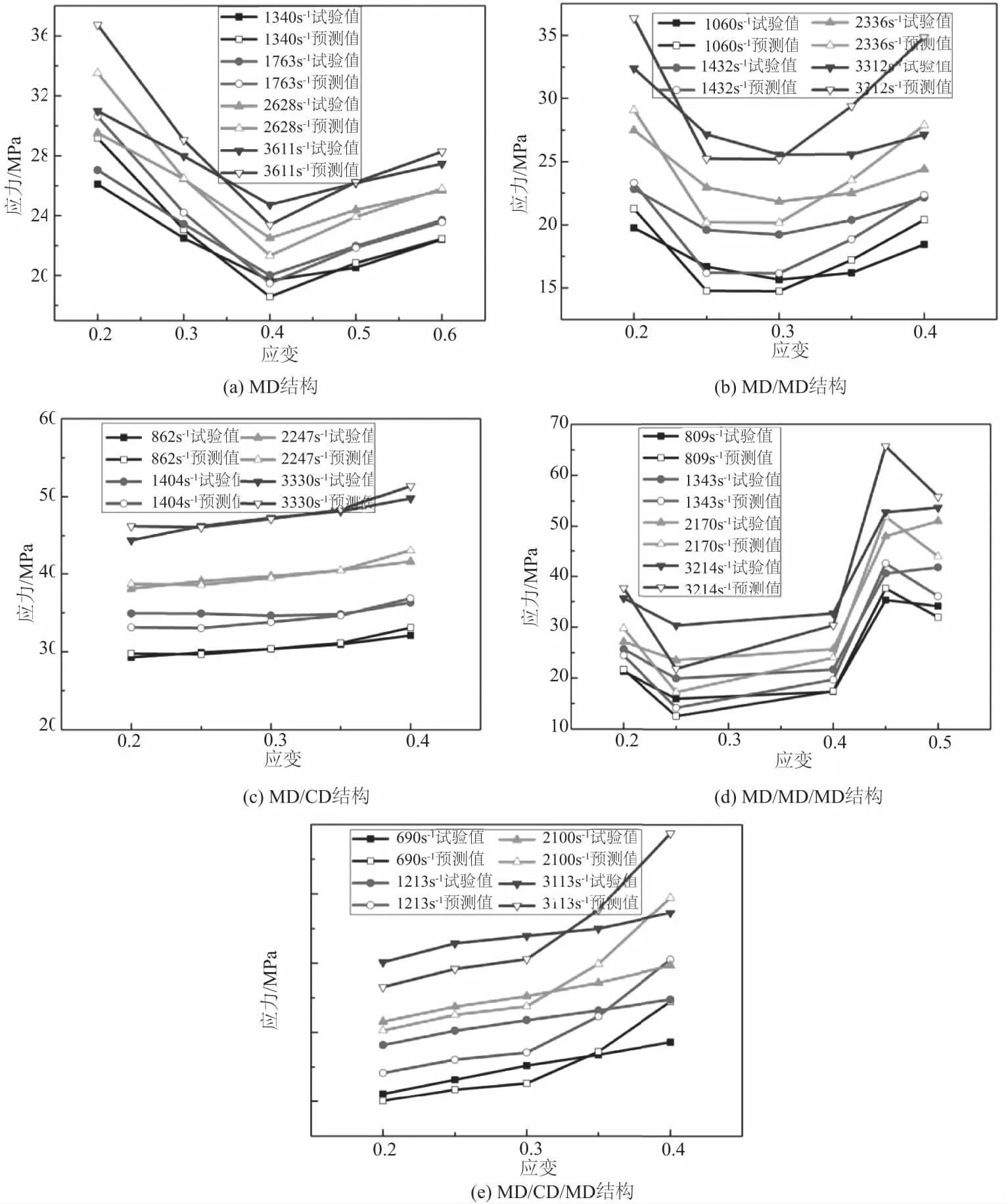
图6 Perzyna经验模型预测值与试验值比较
3) 利用Perzyna经验本构模型计算的应力值与试验值作比较,MD/CD结构最为接近,MD/MD结构相差最大。
