基于模糊控制的数控机床几何误差补偿控制研究

栗江 ，张慧 ，曾祥苹

(1. 广州南洋理工职业学院 机电系，广东 广州 510925 ； 2. 宁夏职业技术学院 工业工程学院，宁夏 银川 750021)

0 引言

随着我国科学技术的不断进步，机械制造业正面临着巨大的挑战。机床是机械制造业最主要的设备之一。机床由于运动过程中经常存在误差，导致机床的加工精度达不到加工要求。时至今日，机床的几何误差的研究逐渐受到专家学者的青睐，并进行了大量的研究。郭世杰等人对数控机床几何误差的相关性分析方法进行了研究[1]；齐继宝等人基于微分变化构造法提出了数控机床几何误差的补偿方法[2]；邹华兵等人基于三轴数控机床的几何误差进行了测量并且对数控机床的几何误差的辨识进行了一定的研究[3]；黄克等人基于检验试件的方法对五轴机床的几何误差进行了分析并对其精度预测进行了研究[4]；郭然等人基于切比雪夫多项式对数控机床几何误差进行了参数化建模[5]；丁小瑞等人对机床切削力和机床的几何误差进行了有限元分析[6]；韩飞飞等人对精密数控机床的几何误差进行了理论建模并通过实验研究验证了可行性[7]；刘宝俊等人对龙门铣床的几何误差模型进行了构建，并且基于所建立的模型提出了补偿策略[8]；王维等人对数控机床几何误差与工作过程产生的热误差进行了综合建模[9]；程强等人基于敏感度分析对机床关键性几何误差进行了识别方法的研究[10]；王金栋等人基于激光跟踪仪对数控机床几何误差的辨识方法进行了研究[11]；刘焕牢等人重点研究了数控机床几何误差测量方法及几何误差的补偿技术[12]；张虎等人基于软件补偿技术研究了多轴数控机床几何误差的补偿方法[13]。虽然国内外对机床的几何误差的研究逐年增多，但是大都集中在机床的几何误差的识别等方面，关于几何误差补偿的研究大都集中在基于数学模型的补偿方法，基于模糊控制的补偿方法的研究稍微成熟，因此，本文基于模糊控制理论对机床的几何误差进行补偿研究，将对机床的几何误差的补偿有着较强的指导意义。

1 数控机床的几何误差模型

描述机床的几何误差的模型有很多，但大都是针对机床的运动位姿标定的模型，并不能对机床的综合误差进行补偿，因此，本文基于模糊控制建立数控机床的几何误差的模型，可以有效地对数控机床的几何误差进行补偿。机床由刀具、主轴及其他部件组成，是1个典型的多体系统，针对多体系统一般采用低序体阵列进行描述，具体的低序体阵列的过程如式(1)-式(10)所示。

将典型的多体系统中的Bj的n阶低序体定义如式(1)所示。

Ln(j)=i

(1)

其中，L为算子，并且n阶高序体与n阶低序体的关系定义如式(2)所示。

Ln(j)=[Ln-1(j)]

(2)

定义L0(j)=j,L0(0)=0当Bj和Bi为相邻低序体时，

L(j)=i

(3)

考虑机床运动是3个方向的转动和平动，为了更准确地研究机床的几何误差，首先将相邻低序体的转动位姿矩阵沿3个坐标轴进行其次变换，分别如式(4)-式(6)所示。

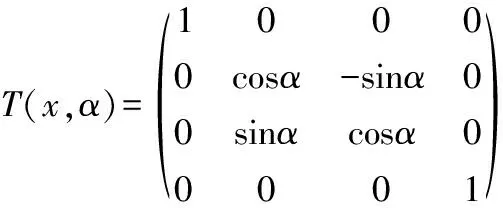
(4)

(5)

(6)

机床的平动的位姿矩阵如式(7)-式(9)所示。

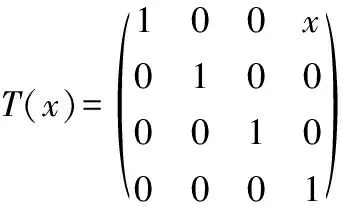
(7)

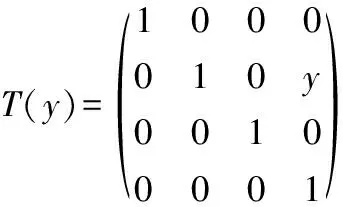
(8)

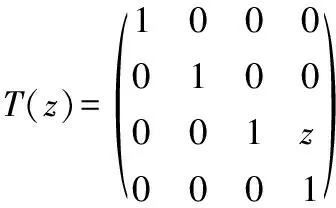
(9)

考虑机床的综合误差由沿x方向的误差、y方向的误差及z方向的误差共同构成，定义沿x方向、y方向及z方向的平动误差分别为δxx、δyx及δzx，沿x方向、y方向及z方向的转动误差分别为εxx、εyx及εzx，综上所述，基于误差叠加原理，建立相邻低序体沿x轴的位置误差如式(10)所示。

(10)

同理可以求得沿y轴和z轴的位置误差，本文不再赘述。

2 基于模糊控制的几何误差的补偿

图1描述了基于模糊控制的机床的控制系统的架构形式。通过图1可以看出：机床的主体部分由逻辑算数单元及单片机构成，控制系统中添加了反馈回路，反馈回路的控制主要是基于模糊逻辑控制理论构成的模糊控制器。

基于本文所建立的机床控制系统对机床的运动位置进行仿真，仿真重点探究基于模糊控制的机床的平动几何误差在不同阵型的误差精度。考虑z轴的平动较小，在进行仿真之前首先定义仿真的y轴和z轴的输入阵型如式(11)和式(12)所示。

(11)

(12)

仿真过程基于MATLAB12.0进行，仿真完成后通过非线性回归得到输出的y轴和z轴的阵型如式(13)-式(14)所示。

(13)

(14)

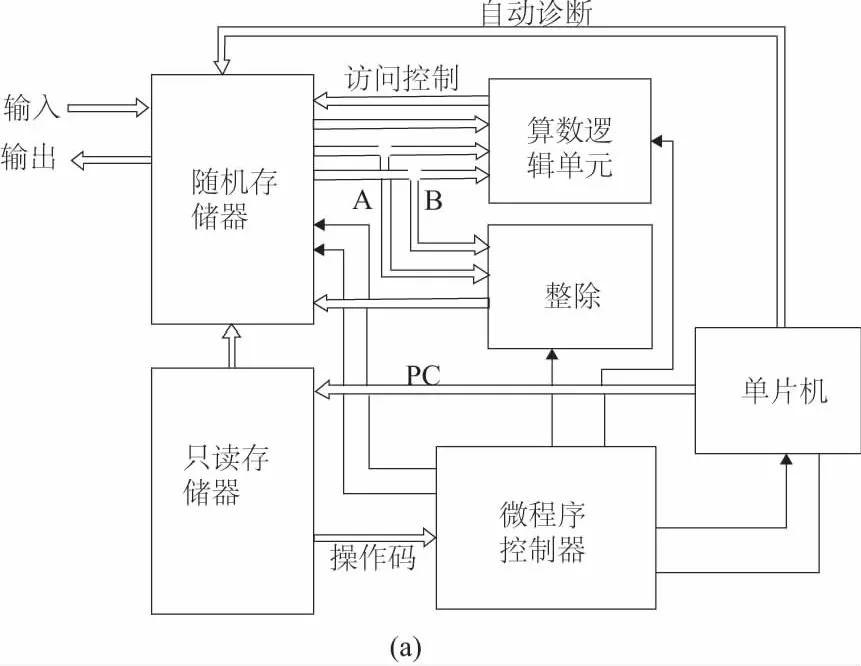
图1 机床控制系统架构形式

通过比较y轴和z轴的输入和输出可以看出：基于模糊控制的y轴和z轴的输出阵型多了z2项，基于MATLAB12.0的仿真结果绘制基于模糊控制的机床的沿y轴和z轴的运动误差系数的变化趋势如图2(a)和图2(b)所示。

通过图2可以看出：不同的激振频率下的y轴的误差系数值基本保持恒定，仅有当激振频率为b2时误差的系数值存在一定的跳跃，并且跳跃程度较小，并且当激振频率较低时，y轴的误差系数基本不受激振频率的影响；通过图2(b)可以看出：不同激振频率下的z轴的误差系数值存在较大的区别，说明激振频率对z轴的误差系数的影响较y轴大，并且误差系数随着激振频率的增大呈现出先增大后减小的现象。

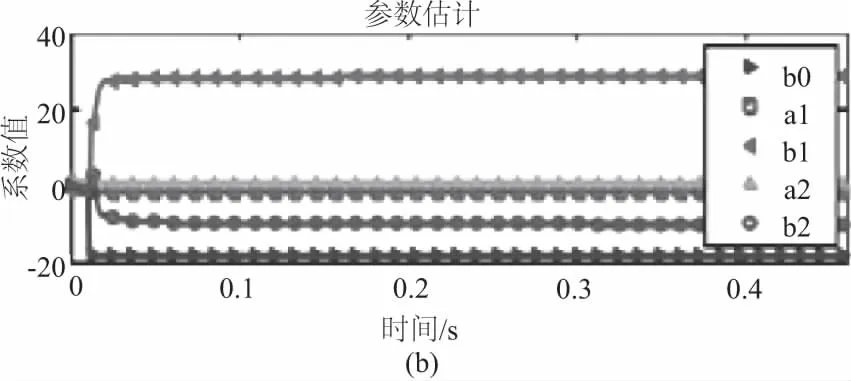
图2 仿真结果

为了验证仿真结果的准确性，本文基于模糊控制理论对数控机床的运动位姿进行实验验证，实验原理如图3所示，图4为基于模糊控制理论的y轴和z轴的运动误差的系数实验结果。

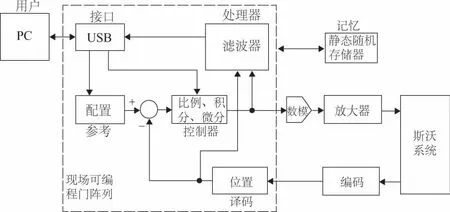
图3 实验原理

图4为基于模糊控制理论建立的机床误差补偿控制系统的y轴和z轴的误差系数的关系图。通过图4(a)可以看出：实验下的y轴的误差系数值存在一定的波动，究其原因认为：机床在工作过程中，激振频率易和机床的固有频率引起共振[14]，因此，会导致误差的系数值存在一定程度的波动；通过图4(b)可以看出：z轴的误差系数值存在的波动程度较低。比较图4和图2的实验结果和仿真结果可以看出：基于模糊控制的机床误差补偿控制系统可以有效地减小机床因运动位姿的改变导致的机床几何误差，实验值和仿真值有着极高的一致性。

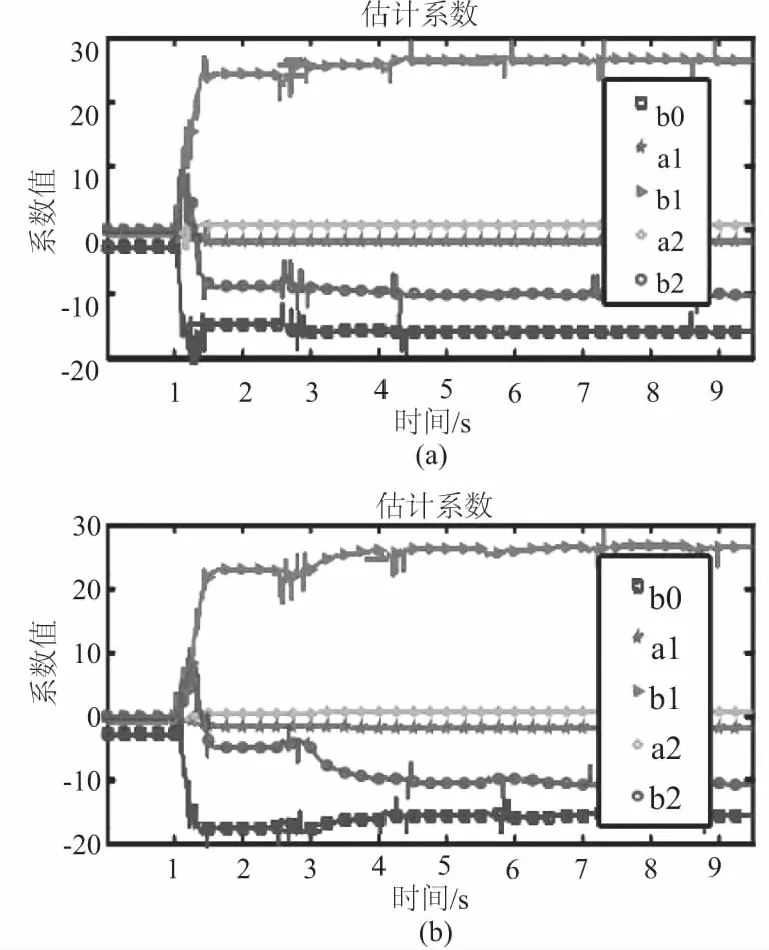
图4 实验结果

3 结语

本文以传统机床的几何误差为研究对象，考虑机床为多体系统，建立了相邻低序体和高序体的沿x轴、y轴及z轴平动和转动的位姿误差矩阵；基于模糊控制理论和所建立的沿x轴、y轴及z轴平动和转动的位姿误差矩阵，建立了基于模糊控制的机床控制系统构架体系，使用MATLAB12.0对不同激振频率下的y轴和z轴的误差系数进行了分析，最后通过实验对仿真所得的误差系数进行验证。通过验证发现：基于模糊控制的机床误差补偿控制系统可以有效地减小机床因运动位姿的改变导致的机床几何误差，实验值和仿真值有着极高的一致性，说明本文所建立的基于模糊控制的机床误差补偿控制对机床的几何误差的补偿等方面的研究起着较强的指导意义。