基于多尺度模糊熵和主成分分析的轴承故障特征提取

李生鹏，韦朋余，丁 峰，竺一峰，姜朝文，周舒豪

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

轴承是船用旋转机械系统中的重要组成部分，诸如主机、尾轴、泵系、锚机等众多设备中，轴承是

收稿日期：2018-07-30必不可少的机械零件。轴承起着承受载荷和传递载荷的作用，其能否正常工作直接影响着整机系统的运行状态。轴承在实际运转过程中承受着复杂交变的外部载荷，致使其成为最容易损坏的零件之一，转动类船舶机械系统发生的故障大约有30%是由轴承损坏引起的[1]，如果能够有效地识别、处理轴承故障，对整机的维护具有重要意义[2]。现有的振动信号分析方法根据定量确定故障的类型以及发展趋势，可以有效防止“维修不足”和“维修过度”[3]。

定量状态下的轴承故障特征与故障类型一般为非线性关系，而能够表征该特征的向量具有数据量大、变量多等特点，如何有效提取不同故障类型轴承振动信号的特征向量成为目前众多学者的研究方向[4]。传统的频谱分析方法已不适用于分析非平稳、非线性的轴承振动信号，而短时傅里叶变换、小波分析等新方法也没有摆脱傅里叶变换的局限性[5]。EMD方法根据自身的时间尺度特征进行分解，具有自适应、完备性和正交性等特点，无需设定基函数，解决了信号在分解过程中瞬时频率难以确定的问题[6-7]。模糊熵利用指数函数的连续性和非突变性进行时间序列的求解，保证了结果的平滑性[8]。轴承故障振动特征频段和复杂程度在不同尺度下均表现出一定的差异性，在多尺度下提取信号的模糊熵值可以提高特征向量的准确性[9]。PCA是一种多元统计方法，可以有效地消除数据之间的相关性并对其进行压缩，实现了降低维数的目的[10-12]。

本文提出了一种多尺度模糊熵和主成分分析相结合的滚动轴承故障特征提取方法。首先利用EMD将原始振动信号分解成若干个IMF，并根据相关系数和峭度值准则剔除虚假IMF分量；然后在不同尺度下求取真实IMF分量的模糊熵值，利用PCA对其进行降维处理，形成能表征不同轴承故障的特征向量；最后借用支持向量机对轴承故障进行诊断验证。

1 轴承特征向量提取

1.1 IMF多尺度样本熵特征提取

EMD方法用于把非线性、非平稳的时间序列分解成有限个IMF，并且每个IMF分量中都含有不同时间尺度的振动信息，其分解过程如图1所示。

1.2 基于峭度准则和相关系数的IMF筛选

EMD分解过程中根据原始信号的局部最大值和最小值点分别拟合成相对应的上下包络曲线，但在实际分析时因为误差、边界效应等原因致使上下包络曲线并不会完全对称。这就会造成实际的EMD运用和理论的EMD分解存在偏差，而这种偏差的存在导致了原始信号中能量的泄露，即得到的IMF存在虚假分量。由EMD分解得到的IMF分量具有正交性，不同分量之间的重合率不超过1%，特殊情况下不超过5%，但由于能量泄露的原因，分解出的虚假分量会与真实分量出现重合，如果不予以剔除则会增加所提取特征向量的维数，带来很大的计算量。在此结合先前学者的研究成果和轴承故障诊断的特点，提出两条准则以剔除EMD分解过程中出现的虚假分量。

图1 EMD算法流程图Fig.1 Algorithm flow chart of EMD

准则1：相关系数准则

根据EMD分解定义可知不同IMF分量都是从原始信号中剥离而来，真实IMF分量与原始信号的关系最为密切，通过计算各阶IMF分量与原始信号的相关系数即可判断真伪，其公式为：

式中：RIMFj为各阶IMF通过公式（1）计算出的结果；N为信号的采样点数；j为IMF分量的阶数。在分析两个时间序列的相关程度时，当ρ（）j的值大于0.5即可认为两者之间的相关程度性较好，即判定为真实分量。

准则2：峭度准则

峭度的定义是描述振动信号波形尖峰度的无量纲参数，其计算公式为：

式中：μ、σ分别表示信号x的均值和标准差。

信号的峭度值和机器的运行状态有关，在轴承平稳工作时采集的信号属于正态分布信号，此时的峭度值约为3。当轴承发生内圈、滚动体和外圈故障时，其波形尖峰会增加，造成信号明显偏离正态分布而使峭度值变大。EMD分解得到的IMF分量为不同频段的信号，每个部分所包含的振动冲击不一样，其峭度值越大则表示该IMF分量所携带的故障信息越多。因此本文选取峭度值大于3的IMF分量作为真实分量予以保留。

1.3 基于多尺度模糊熵的IMF特征提取

模糊熵用于衡量时间序列在维数变化时所产生新模式概率的大小，产生概率的值越大则模糊熵值越大。模糊熵通过选择指数函数e-（d/r）n（n，r分别为模糊函数边界的梯度和宽度）作为模糊函数来计算两个向量的相似性，使其具有连续和不突变性，且保证了自相似值的最大，其计算过程如下：

（1）对时间序列 ｛u（i）:1≤i≤N｝进行处理得到m维向量：

式中：i,j=1,2,…,N－m,i≠j。

（4） 定义函数

（5）根据以上步骤构造m+1向量：

（6）根据以上步骤可得模糊熵值为：

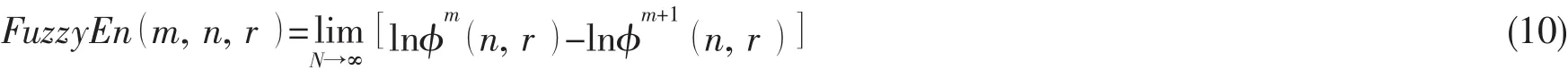
当N有限时，上式可变化为

轴承不同故障振动信号特征频段和复杂程度在不同尺度下表现出一定的差异性，在不同尺度下提取其振动信号的模糊熵值可以提高结果的准确性，其定义为对N点时间序列Xi=｛x1,x2,…,xn｝进行粗粒化处理，形成新的时间序列：

式中：τ=1,2,…,n为尺度因子。

多尺度模糊熵表示为在不同时间尺度下求取振动信号的特征模糊熵值，可以有效地克服单一模糊熵值用于衡量时间序列的缺陷。

2 基于PCA的特征向量降维

在上一节求取了轴承故障的特征模糊熵值，但尺度因子一般要取10以上，对多个IMF进行计算得到的特征向量会更多。但不是每个特征值对识别轴承故障类型的贡献率都是一致的。如果将所有特征值都用于故障识别，势必会增加运算的数量和时间，出现信息冗余和维数灾难的问题，在此利用PCA对其进行降维处理。

设提取的轴承特征信号列向量为Xk=［x1k,x2k,…,xnk］，每组特征信号中有n个特征值，则轴承当前的状态可以用xk描述，其协方差矩阵为：

式中：N为样本的数量，¯为各模式向量的均值。

求取Rx的特征值λi=（i=1,2,…,n）和特征向量vi，通过对λi进行排序形成相对应新的特征向量vi（i=1,2,…,n）。 计算样本xk投影vi即可得到对应的主分量：

所有的特征向量形成一个n维正交空间，x通过投影可以得到n维主分量，在投影过程中对应的特征值越大则在重构时的贡献率也越大，反之则越小。设正交空间的前m主分量为y1,y2,…,ym，其累计方差的贡献率为：

当前m主分量的贡献率足够大时就可直接利用该分量进行故障诊断，在保证信息完整性的前提下实现降维的目的，本文取累计贡献率大于90%的数个主分量作为故障诊断的特征值。

本文的轴承故障特征提取步骤如图2所示。

图2 轴承故障特征向量提取流程示意图Fig.2 The schematic diagram of extraction procedure for rolling bearing fault feature vector

3 实验装置及数据采集方式

本次实验采用的是美国西储大学轴承实验平台，如图3所示。实验平台的左侧为2马力的电机，中间部分为转矩传感器，右侧为功率计。

实验中电机的转速为17 501 rpm，采样频率为12 kHz，分别采集了正常状态、内圈故障、滚动体故障和外圈故障共4种轴承数据，其时域波形如图4所示。

图3 机械故障模拟实验台Fig.3 Simulation test-bed of the mechanical fault

图4 4种状态滚动轴承原始振动信号Fig.4 Original vibration signal of four states for the rolling bearing

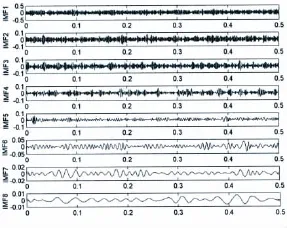
图5 轴承外圈故障EMD分解结果Fig.5 The EMD decomposition result of bearing outer ring fault

4 实验验证

该实验平台共有正常、内圈故障、滚动体故障和外圈故障4种类型。对每种类型的振动数据采集50组，随机挑选25组用于训练，剩余25组用于测试，每组数据包含6 000个采样点。对采集到的轴承外圈故障进行EMD分解得到8阶IMF分量，结果如图5所示。

对轴承不同状态下振动信号分解出的8阶IMF分量进行相关系数和峭度值计算，结果如表1、表2所示。

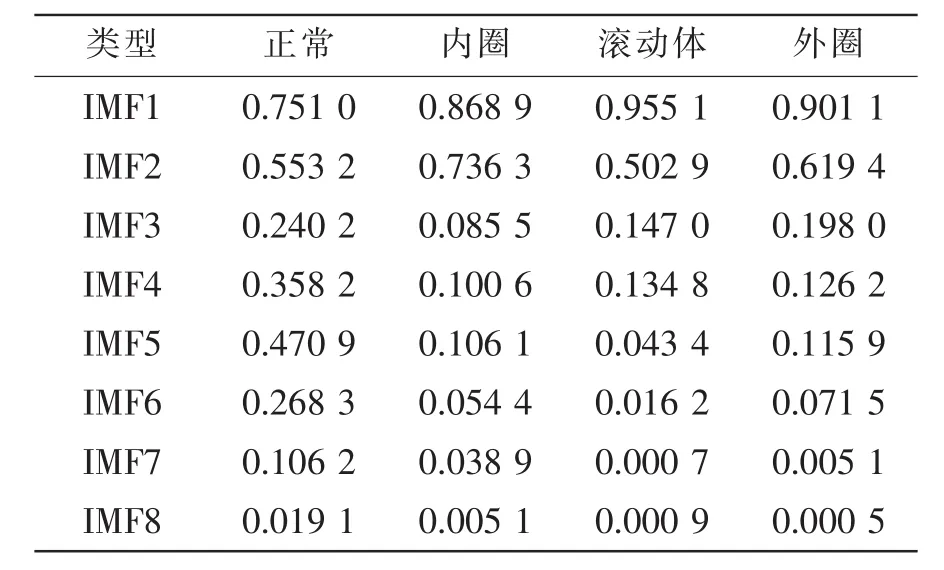
表1 四种状态轴承相关系数Tab.1 Four state correlation coefficients of the rolling bearing

表2 四种状态轴承峭度值Tab.2 Four states kurtosis value of the rolling bearing

由表中可知IMF分量峭度值和相关系数较大的主要集中在IMF1和IMF2分量中，但正常和滚动体故障的峭度值大于3的IMF分量不止2个，为了方便数据处理形成统一维数的输入向量，在此选取峭度值最大的2个IMF分量予以保留，将其余的分解剔除。在不同尺度下计算轴承不同状态IMF1和IMF2分量的模糊熵值，本文选择尺度因子为20，结果如图6、图7所示。

图6 IMF1多尺度模糊熵Fig.6 IMF1 multiscale fuzzy entropy

由上图可以看出，很多尺度因子对应的模糊熵值相差很小，而且并不是每个特征值对故障诊断都是有用的，如果不对其进行降维则会增加运算量，出现维数灾难等问题。在此基于PCA对其进行处理，由于篇幅有限，本文只给出了外圈故障IMF1降维的结果，如表3所示。

由表3可知，前3个主分量的累计贡献率已经超过了90%，故可以用这3个主分量作为轴承故障诊断的特征向量。在此借用支持向量机作为分类机器，每种类型的振动数据采集50组，随机挑选25组用于训练，剩余25组用于测试。对所有样本的IMF1、IMF2分量都进行多尺度模糊熵计算，然后利用PCA进行降维处理，将最终的特征向量输入支持向量机进行训练、测试，其结果如图8所示。

图8中1、2、3、4分别代表正常、内圈故障、滚动体故障和外圈故障4种状态，其中内圈故障有1个样本被识别为正常状态，滚动体故障有2个被识别为外圈故障，外圈故障分别有1个被识别为滚动体故障和内圈故障。分析原因可能是利用PCA对多尺度模糊熵进行降维时只采用了累计贡献率达到90%的主分量，在筛选IMF分量时根据准则值选取了2个，丢失了部分特征信息，不过总体分类精度达到95%（如图8中所示，错位点占5%），证明本文的方法是一种有效的轴承故障诊断途径。

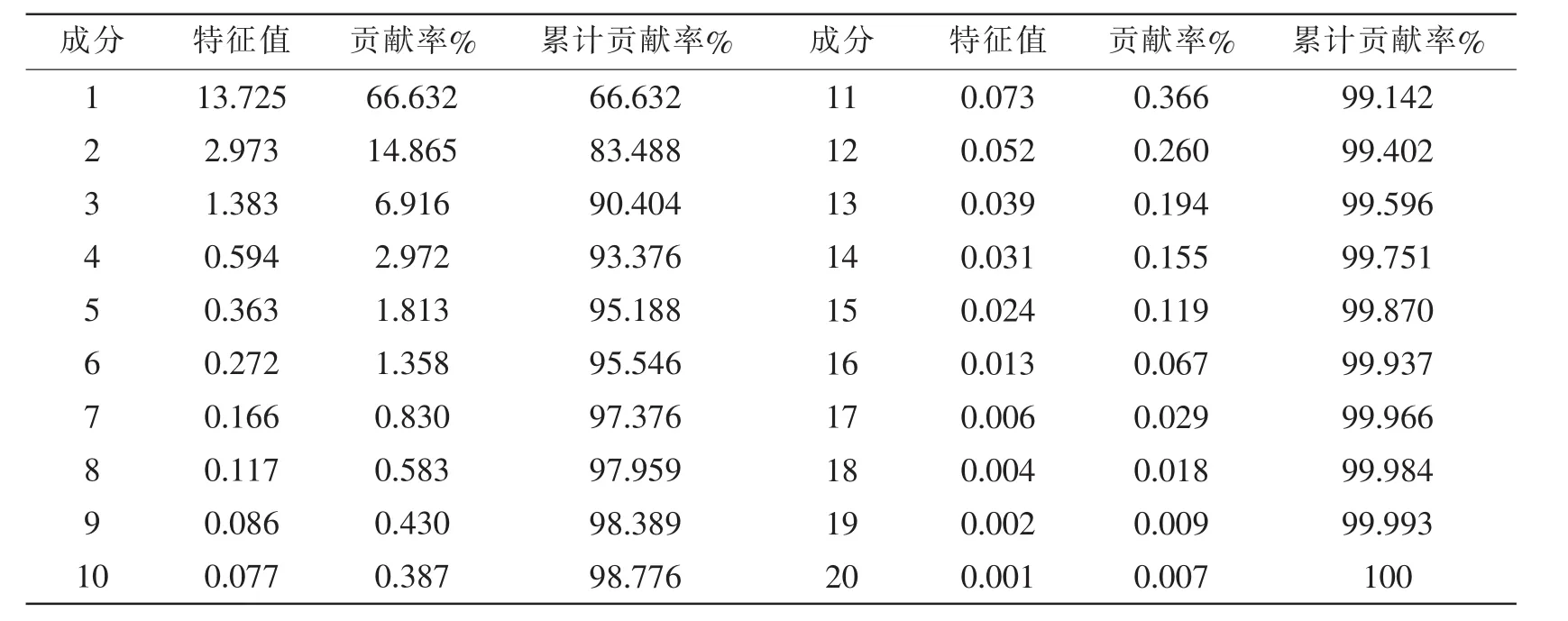
表3 外圈故障IMF1降维的结果Tab.3 The result of IMF1 reducing dimensions for outer race fault

为了证明虚假分量筛选的有效性，在此求取经EMD分解后的前8阶IMF分量模糊熵值，结果如图9所示。

图8 支持向量机诊断结果Fig.8 Diagnosis result using support vector machine

图9 IMF分量模糊熵Fig.9 The fuzzy entropy of IMF component

计算每种故障类型振动数据的特征模糊熵值，在此借用支持向量机作为分类机器，每种类型的振动数据采集50组，随机挑选25组用于训练，剩余25组用于测试，其结果如图10所示。

由图10可知，由8阶IMF分量求取模糊熵得到的特征向量识别准确率为88%（如图10中所示，错位点占12%）。分析其原因可能是由于虚假分量的存在，从第5阶IMF开始得到的模糊熵值非常小且趋近于0，不同故障类型之间的模糊熵值差别不大，从而分类界限不明显导致了识别正确率较低。

图10 未筛选IMF支持向量机诊断结果Fig.10 Diagnosis result using support vector machine for unfiltered IMF

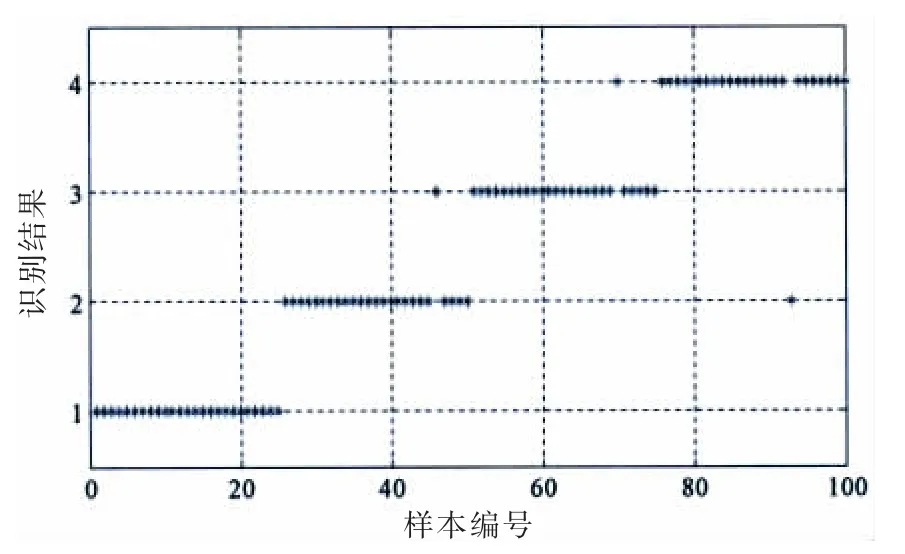
图11 未经PCA降维支持向量机诊断结果Fig.11 Diagnosis result using support vector machine for non-reducing dimension through PCA

为了证明PCA降维的有效性，在此将求取IMF1、IMF2共40个特征向量输入支持向量机进行验算，识别结果如图11所示。利用MATLAB的tic、toc组合函数测试分类所用的时间，仿真电脑参数如表4所示，其结果如表5所示。

由表5可知，未经PCA降维的支持向量机识别精度为97%，识别时间为17.361 s，而经过PCA降维处理后的特征向量识别时间为10.592 s。综上实验可以表明在牺牲少量识别精度的前提下可以大幅度减少识别所用的时间，证明了降维的有效性。

表4 仿真电脑参数Tab.4 The parameters of simulation computer

表5 仿真结果统计Tab.5 The statistics of simulation result

5 结 论

针对轴承故障特征难以提取的问题，本文提出了基于多尺度模糊熵和主成分分析相结合的滚动轴承故障特征提取方法。首先利用EMD将原始振动信号分解成若干个IMF，并根据相关系数和峭度值准则剔除虚假IMF分量；然后在不同尺度下求取真实IMF分量的模糊熵值，利用PCA对其进行降维处理，形成能表征不同轴承故障的特征向量，最后借用支持向量机对其进行诊断验证。主要结论归纳如下：

（1）EMD基于信号自身局部特征时间尺度分解非线性、非平稳轴承故障信号，得到的IMF分量能够突出原始信号的不同局部信息，有利于特征信息提取。

（2）实验结果表明，未经筛选的IMF分量识别精度为88%，低于最终识别精度95%。分析原因可能是阶数较大的虚假IMF分量差别较小，导致数据的相似度较高、难以区分，证明了筛选的必要性。

（3）轴承故障振动的信号特征频段和复杂程度在不同时间尺度下表现出一定的差异性，提取其振动信号的多尺度模糊熵值提高了识别结果的准确性。

（4）经PCA降维后的特征向量识别精度为95%，低于未经PCA降维的97%，但识别时间从17.361 s降低到了10.592 s，即在牺牲少量识别精度的前提下大幅度减少识别所用的时间，说明了降维对识别结果的有效性。