切口节点疲劳试验及损伤演化仿真研究

孙 迪 ， 甘 进 ， 吴卫国

（1.高性能舰船技术教育部重点实验室（武汉理工大学），武汉 430063；2.武汉理工大学 交通学院，船舶、海洋与结构工程系，武汉 430063）

0 引 言

船舶与海洋工程等钢结构由于长期处于波浪等循环载荷环境中，其结构很容易发生疲劳破坏的现象，因此在设计过程中考虑结构的疲劳强度是十分有必要的[1]。事实上，疲劳破坏经常发生在局部连接构件节点的位置，这些构件由于几何形状的突变、焊接残余应力等因素，往往最容易发生疲劳破坏[2]。所以结构连接节点处的疲劳强度应该给予更多的重视。由于船舶与海洋工程结构中的加工工艺原因，在构件的连接节点处肘板与骨材无法实现圆弧切线过渡，因此在肘板与骨材连接的端部会存在阶梯型的切口，而这样的切口由于几何形状的突变往往会造成应力集中从而在肘板与骨材连接的切口处发生疲劳裂纹萌生[3]。

在钢结构中疲劳破坏是一个损伤累积并且是不可逆的过程，其主要表现为材料内部特性的劣化过程，具体主要是裂纹的形核、微裂纹的扩展、脱粘、空洞等等[4]。目前国内外的专家和学者主要是基于疲劳试验和传统的疲劳分析方法对船舶与海洋结构进行疲劳性能研究。由于疲劳试验的研究成本高、周期长，理论分析在疲劳研究领域是一个重要途径[5]。众所周知，当材料或结构的S-N曲线、ε-N曲线及外载荷已知的情况下，预测疲劳寿命的准确度依赖于疲劳累积损伤准则的合理性，因此很多理论研究工作集中在疲劳累积损伤理论上[6-7]。基于连续损伤力学（CDM）的疲劳累积损伤理论研究是当前研究热点之一。将连续损伤力学中合理的疲劳损伤演化方程与有限元方法结合应用到疲劳问题中预测疲劳寿命是一种非常经济有效的应用手段，疲劳领域也是CDM最具有应用前景的领域[6]。1988年，Chaboche等[8]首次系统地将CDM方法用于疲劳寿命预测中，Lemaitre等[9-10]根据CDM理论，先后提出了3个疲劳损伤演化方程。Kim等[11]发展了Chaboche的损伤演化方程，并用于疲劳蠕变寿命预测。Xiao等[12]发展了一个可以考虑平均应力效应的高周损伤演化方程。

目前广泛应用于疲劳损伤演化的损伤力学模型主要有两类：一是Chaboche模型及其各种简化模型，它是基于疲劳损伤曲线直接构造损伤演化函数而建立的，有较好的普适性；另一类是Lemaitre模型，它从热力学耗散理论推导得到，实质上为一延性损伤模型，损伤与塑性应变直接相关[7]。

本研究中首先对材料进行标准试件拉伸试验得到材料的基本参数，然后对切口试件进行一系列典型工况下的疲劳试验，获得典型节点在不同载荷水平下的疲劳寿命值。在数值仿真方面，选取合适的损伤演化模型，并采用非线性拟合方法拟合试验数据得到模型相关参数。通过对ABAQUS软件进行二次开发，实现损伤演化模型与单元刚度耦合的子程序计算。最后将有限元仿真结果与疲劳试验结果对比，验证仿真的可靠性并对切口节点的疲劳损伤演化规律进行相关分析。

1 切口试验

1.1 切口试件模型几何尺寸

在船舶结构中存在着大量的肘板与骨材结构连接的节点部位，这些节点的典型连接方式有类似一个垂直的阶梯切口的连接形式[13]，如图1所示，这些地方由于几何的突变导致在垂直切口部位产生应力集中从而导致疲劳裂纹在该处产生。因此本实验基于船体肘板与骨材结构连接节点的垂直切口处为试验对象来设计疲劳试验模型。

图1 船体典型节点连接方式Fig.1 Typical joint of ship structure

图2 切口试件几何形状及尺寸Fig.2 The geometry and dimension of notched specimen

如图2所示，由于船体连接节点中存在大量垂直切口，因此本文设计了一个标准垂直切口试件用于疲劳试验。图2（1）中的切口试件的外形轮廓参照 GB/T 13816-1992[14]中的规定。试件采用线切割的加工方法，图2（2）中的红圈（A）处为模拟船体结构中的节点连接处垂直切口位置。

1.2 试验试件材料参数测试

用于试验试件的材料为Q345钢。如图3所示，为了获得Q345钢准确的材料性能相关参数，在疲劳试验前首先进行了一系列静力拉伸试验。静力拉伸试验规程参照GB/T228-2002[15]中进行测试。试验测得的材料性能相关参数如表1所示。

表1 Q345钢相关力学性能Tab.1 Mechanical properties of Q345D steel

图3 Q345钢标准试件拉伸测量试验Fig.3 Tensile tests and specimen

图4 切口试件疲劳试验Fig.4 The assembly of the notched specimen

表2 恒幅疲劳试验加载工况Tab.2 Loading conditions of CA loading tests

1.3 切口试件疲劳试验

试验在武汉理工大学交通学院结构实验室完成，采用MTS伺服液压试验机。如图4所示，切口试件两端由试验机的夹头进行固定，其中一个夹头固定在试验机平台上，另一个夹头为伺服液压控制的作动器进行循环载荷的加载。疲劳载荷采用恒幅正弦波加载，采用力控制的加载方式，应力比为R=0.1，加载频率固定为15 Hz。当试件完全疲劳断裂时停止试验。由于该试件疲劳裂纹扩展寿命与疲劳裂纹萌生寿命相比占很小一部分，因此本实验认为该切口试件的疲劳破坏寿命为疲劳裂纹萌生寿命。

表2为疲劳试验的试验工况，一共进行了11个工况的测试，每个工况进行了3次重复试验并取3次重复试验的平均值作为该工况下切口试件的疲劳寿命。

1.4 疲劳试验结果

试验结果表明，疲劳破坏发生在垂直切口处，其断口形式如图5所示。表3为试验测试结果，一般认为疲劳寿命大于107为无限寿命，因此当试件加载107次后仍然没有发生疲劳破坏时则停止疲劳试验。可以看出当应力幅值小于55 MPa时切口试件将不发生疲劳破坏。

图5 切口试件疲劳断口（A）及疲劳破坏处（B）Fig.5 The fracture surface （A） and failure spot（B）of notched specimen

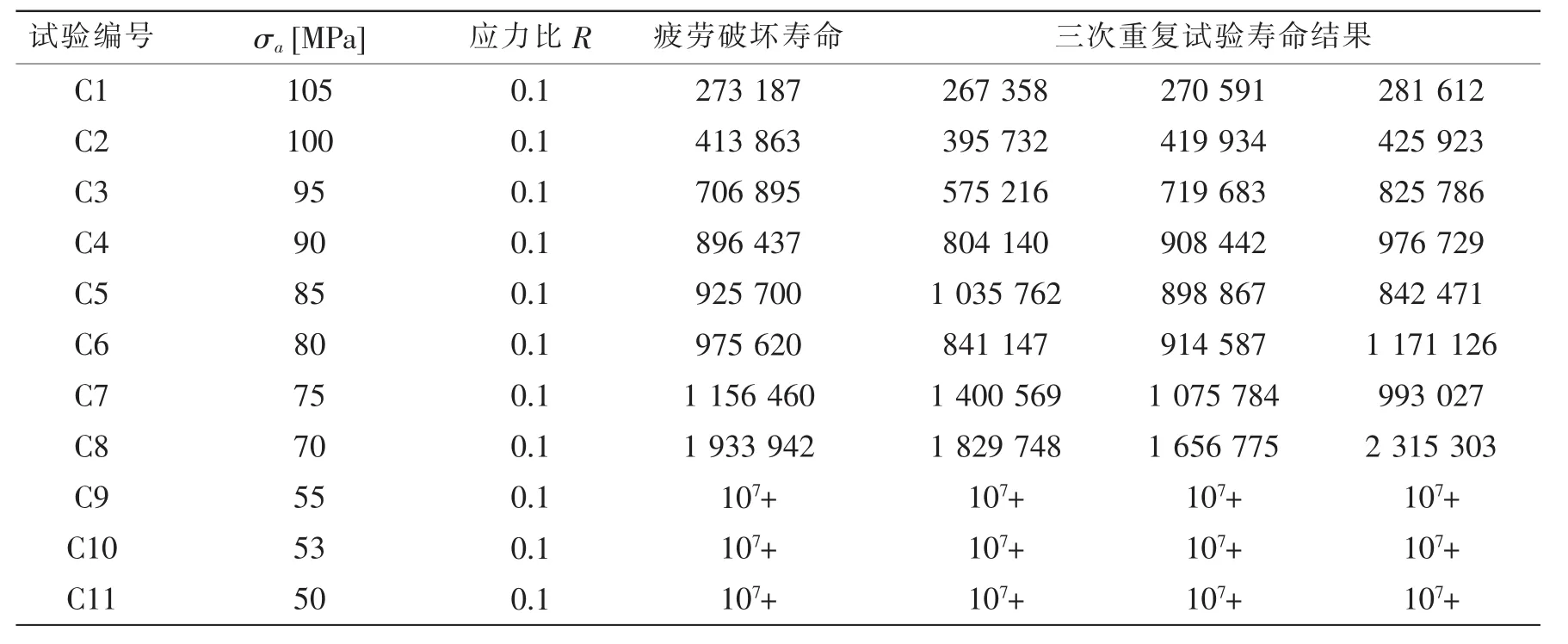
表3 恒幅疲劳试验结果Tab.3 CA loading tests of notched specimens

2 疲劳损伤模型

Chaboche等[8]建立了基于损伤力学理论的疲劳损伤演化方程，其具体形式如下：

其中：参数M0和b由材料疲劳性能确定；σmax和σmed分别是循环应力中的最大应力值和应力平均值；指数α由载荷（σmax，σmed）确定。指数α方程形式如下：

其中：参数a和H通过试验确定。

将疲劳损伤演化方程模型从D=0到D=1积分得到如下的方程形式：

为了便于有限元迭代计算，在损伤区间 ［Di,Di+1］对公式（4）进行积分可得

3 切口节点疲劳累积损伤有限元二次开发

目前应用损伤力学有限元方法分析疲劳损伤问题主要是采用全解耦的方法，将应力场与疲劳损伤场相互独立分开，这种做法随着疲劳损伤累计量逐步增大，会带来较大的误差。目前的大型通用有限元软件并没有一个系统的损伤力学-有限元全耦合的方法分析结构的疲劳累计损伤问题。因此需要对现有的大型通用有限元软件进行相应的二次开发，实现软件的损伤力学-有限元耦合的疲劳寿命计算方法。

损伤力学—有限元耦合方法是指在结构的应力应变场中引入损伤场并结合损伤演化模型对结构的累积损伤过程进行描述。本文采用的方法是将损伤引入到单元刚度矩阵中对平衡方程进行修正，每一个载荷步，程序计算损伤值并对单元刚度矩阵进行修正，通过非线性迭代的方法求出结果。单元刚度的逐渐变化可以用下式表示：

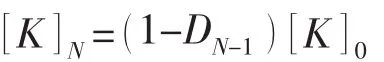
其中：DN-1为循环N-1次后单元产生的损伤；［K］N为修正后的单元刚度矩阵；［K］0为初始刚度矩阵。

为了准确实现损伤力学-有限元法的全耦合方法的疲劳寿命分析，需要每隔一定的应力循环次数后进行单元刚度矩阵的重新计算、组集，以反映疲劳损伤累积效应对单元刚度矩阵的影响。本文采用ABAQUS提供的用户子程序接口UMAT，将损伤演化模型嵌入，通过FORTRAN软件编写用户子程序以实现疲劳损伤对单元刚度的影响。计算每次循环后试件的损伤量，采用损伤力学—有限元法进行耦合疲劳损伤分析，并实现对试件的损伤状态追踪。

在柱坐标系中，对于三维问题，有效损伤弹性矩阵形式为：

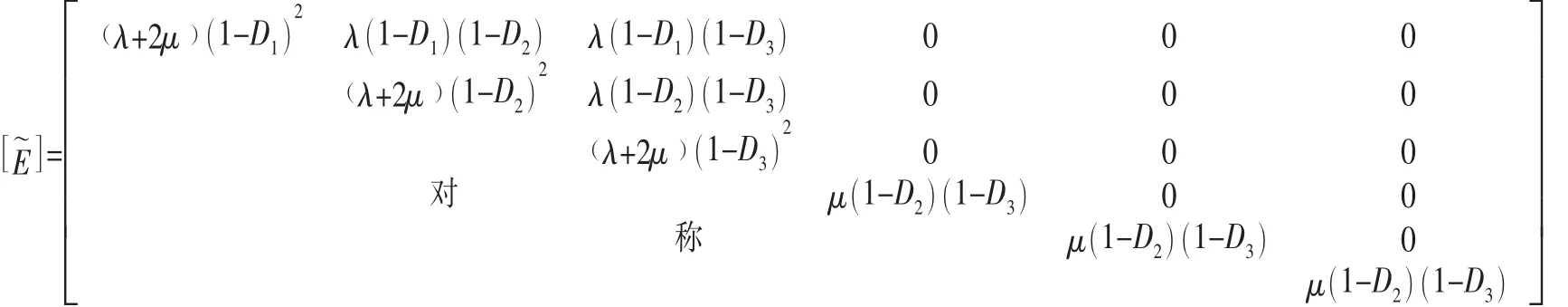
其中：λ，μ为拉梅常数。

设在任意直角坐标系xyz中x，y，z相对于材料主轴 1，2，3 的方向余弦为（l1,m1,n1），（l2,m2,n2），（l3,m3,n3）。设柱坐标系为x1，y1，z1，任意直角坐标系为xyz。对于三维问题，有效损伤弹性矩阵形式可以根据张量的坐标变换关系获得：

4 损伤力学—有限元全耦合切口试件疲劳分析

4.1 切口试件有限元静力计算

在进行切口试件疲劳寿命有限元计算之前首先进行切口试件的静力计算，观察切口试件的应力云图分布，确定有限元网格大小及损伤-刚度耦合计算的网格规模，从而在保证切口试件疲劳分析精度的情况下提高计算效率。

图6给出了切口节点静力计算结果云图，为了精确地建立切口试件的有限元模型，在切口试件垂直切口处通过高倍光学显微镜测量出垂直切口的半径为0.4 mm，因此在垂直切口处有限元网格大小为0.05 mm，逐渐过渡到在远离垂直切口处有限元最大网格大小为3 mm。从云图中可以发现应力最大处为切口试件垂直切口处，因此疲劳破坏发生在切口试件垂直切口处，计算结果与试验现象相符。

4.2 切口试件疲劳寿命计算机损伤演化分析

在进行疲劳有限元仿真计算之前先要获得疲劳损伤演化模型公式（3）的相关参数，假定各级应力范围水平下疲劳寿命分布为对数正态分布，并且在高周疲劳范围内应力幅与对应的疲劳寿命在双对数坐标系下为线性关系，因此采用非线性拟合方 法对试验数据进行拟合，得到公式（3）的相关参数，对于疲劳寿命大于107的工况则不考虑。拟合结果如图7所示。可以看出拟合结果的决定系数为0.94，说明拟合方程与试验数据非常吻合。

图6 切口试件静力分析云图Fig.6 Static simulation of notched specimen

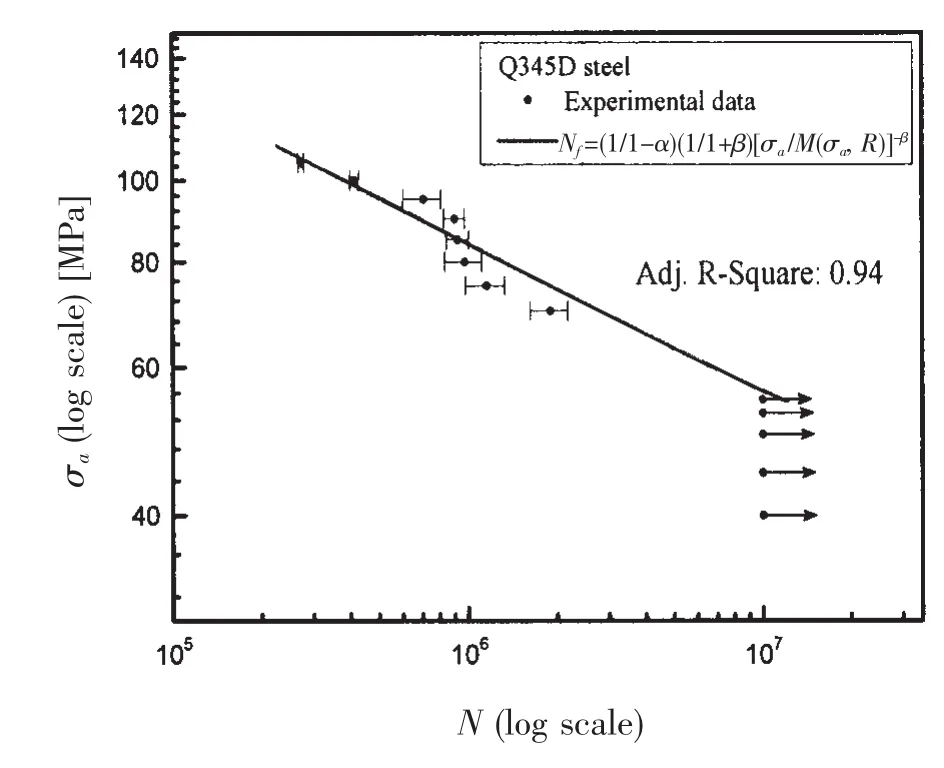
图7 切口试件疲劳试验数据及损伤演化模型拟合Fig.7 Results of experimental data and fitting curve

图8 切口试件疲劳分析边界条件（A）及疲劳分析区域（B）Fig.8 Boundary condition(A)and fatigue analysis region(B)of notched specimen

由于损伤—刚度耦合的有限元疲劳分析方法每一循环步都是非线性迭代，因此计算量大。在保证计算精度的情况下取试件的1/3作为分析对象，其两侧施加对称的边界条件如图8（A）所示，并且只考虑垂直切口周围一定范围区域进行损伤刚度耦合计算如图8（B）所示。材料的弹性模量和泊松比采用拉伸试验测得的值进行输入如表2所示。采用损伤力学—有限元法进行耦合疲劳损伤分析的具体流程如图9所示

为了缩短求解试件，根据实验寿命的大小以及有限元反复计算验证，确定每个计算步疲劳循环次数选取为ΔN=1 000进行试件损伤累计计算，并假设在循环次数步长计算范围内，材料的本构关系不发生变化。疲劳仿真结果如图10所示。图11分别给出了试件的疲劳加载工况下切口试件的疲劳仿真初始加载和疲劳破坏前的应力分布云图；图12给出了试件疲劳仿真加载过程中的损伤分布云图；图13给出了试件疲劳仿真的疲劳损伤演化曲线图。

图9 损伤刚度耦合疲劳分析计算流程图Fig.9 The flow chart of fatigue simulation analysis

5 结 论

本文通过试验和仿真方法研究了切口试件疲劳特性并建立了损伤-单元刚度耦合的仿真方法，实现了切口试件有限元疲劳损伤全耦合计算。通过分析疲劳仿真计算结果，可以得出如下结论：

（1）从图10可以看出仿真结果与试验拟合曲线整体符合较好，说明仿真结果真实可信。但可以发现加载应力幅大时仿真结果与拟合曲线偏差较小，加载应力幅小时仿真结果与拟合曲线偏差较大。

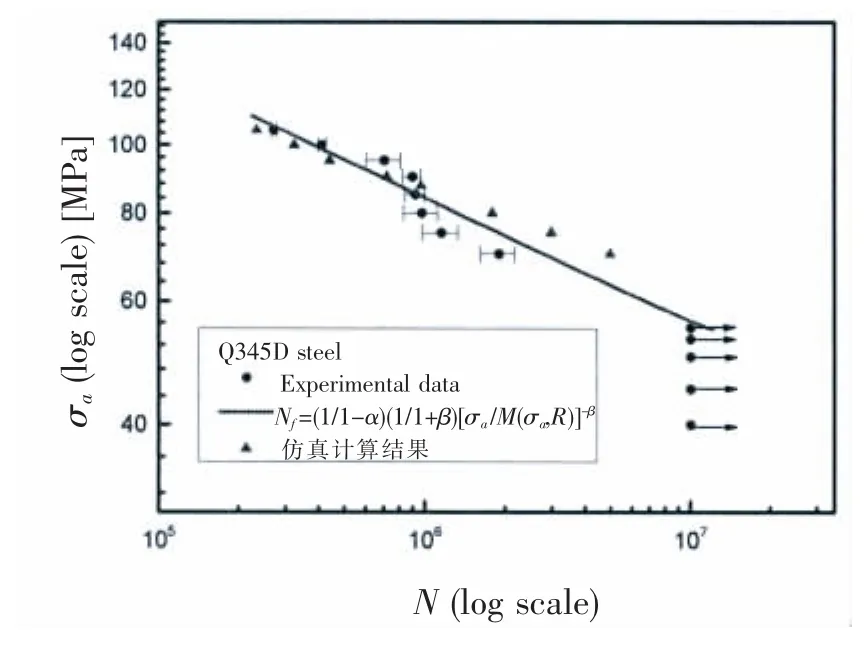
图10 切口试件疲劳仿真结果与拟合曲线对比Fig.10 The comparison of simulation results and fitting curve

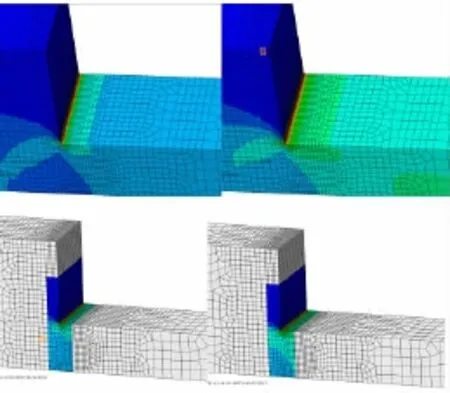
图11 切口试件初始状态与疲劳破坏应力云图对比Fig.11 The stress distribution difference between initial and final of simulation

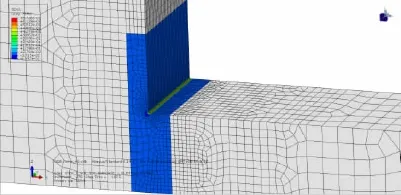
图12 切口试件疲劳损伤分布Fig.12 Damage distribution of notched specimen

图13 切口试件疲劳疲劳损伤演化曲线Fig.13 Damage evolution curve of notched specimen

（2）通过图11中的应力云图对比可以看出，由于切口处的应力较大因此在循环过程中疲劳损伤度增长较快导致切口处刚度下降较周围区域快，因此使得切口周围区域在疲劳加载过程中承载比初始加载较多的载荷，导致了切口周围应力重分布。

（3）通过图12可以看出疲劳损伤发生的主要位置是切口圆弧处以及周围很小的区域，其他区域几乎没发生疲劳损伤。因此切口试件的疲劳损伤只发生在切口局部区域。

（4）从图13可以发现在疲劳加载初期损伤值小于0.05时，疲劳损伤演化速率较大，疲劳损伤增长较快，然后疲劳损伤增长速率逐渐平稳。这是由于切口试件切口根部受到切口周围区域的边界控制，需要与切口周围区域满足变形协调，因此当切口根部损伤增长较快刚度下降较多应变增大时会受到周围区域的变形协调限制导致切口处承受的应力变小从而损伤增长速率又逐渐降低。直到疲劳破坏后期损伤值大于0.7时，疲劳损伤急剧增长直至疲劳完全破坏。