船舶开孔有限薄板横向弯曲振动问题研究

2018-11-02朱竑祯王纬波殷学文高存法

船舶力学 2018年10期

朱竑祯，王纬波，殷学文，高存法

（1.南京航空航天大学机械结构力学及控制国家重点实验室，南京210016；2.中国船舶科学研究中心船舶振动噪声重点实验室，江苏无锡214082）

0 引言

结构上开孔能够起到减重、侦查、维修、通风等作用，在工程中十分常见。带孔薄板在船舶上应用也相当广泛，如消声器内部穿孔板及水下航行器的外壳板等[1]。而圆孔因加工容易且孔边界无奇异点，在潜艇结构中是常用的开孔形状，如在舱壁上布置圆形孔以用于安装主机轴承及鱼雷发射管等装置[2]。静力学中，当结构承受拉伸或挤压时，孔洞附近的最大应力会高于平均应力好几倍，产生了静力学中的应力集中现象[3]，非常容易导致孔洞的变形及结构的破坏。而在动力学中，开孔后板的质量和刚度分布发生变化[4]，整体结构的动力学特性也必定会改变，因此关于含孔而导致的振动变化规律研究对于水下结构的振动控制及降噪设计、声学优化有重要的意义。

目前对于连续薄板的振动研究已经较为成熟，而含孔薄板由于形状复杂，难以用方程准确描述，因而对此的研究并不多，且主要集中于对中心位置含孔的研究。Paramasivam[5]利用差分法求解了正方形板中心含正方形孔的振动问题。Liew等[6]将差分法结合能量法求解了矩形板中心开孔的振动问题。差分法是通过划分区域单元来求解的，用于求解直线边界较为简便，对于曲线边界则难以模拟。Takahashi[7]通过Raileigh-Ritz能量法和由边界条件预设的位移函数求解了矩形板中含孔的振动问题，虽然可以适用于任意位置的孔，但是其对于位移函数的准确性要求较高，因此只能适用于少量有精确解的边界情况，且Hegarty等[8]证实了对于含圆孔方形板使用能量法求解的结果并不准确。Kwak等[9]提出了在孔洞位置和板中心位置分别建立坐标系的方法，对传统的Raileigh-Ritz能量法进行了改进，用于计算任意位置含孔洞的平板振动问题，不过仍然受到精确位移解的限制。而在国内，对于含孔的平板振动问题大多采用有限元法求解[1，10-12]，及沿用能量法求解矩形板的振动[13-14]，对于含偏心孔洞的多种边界的薄板振动理论研究并不多。

本文在比较各类方法后，采纳Hegarty等[8]的计算方法，在内孔的中心建立全局坐标系，使内边界条件精确满足，在外边界上取点，使外边界条件近似满足，并将Hegarty等的工作推广至适用于任意位置的孔洞和多种边界形状，通过算例验证了本文方法的正确性且分析了孔洞偏心对结构的影响。

1 基本方程

本文研究均质各向同性的薄板，薄板上含一个圆孔，圆孔的位置任意，半径为R。薄板的形状为曲线方程已知的规则图形（如圆形、矩形、椭圆等）。如图1所示，以圆孔的中心为坐标原点建立坐标系，基于Kirchhoff的经典薄板理论的平板弯曲自由振动方程为：

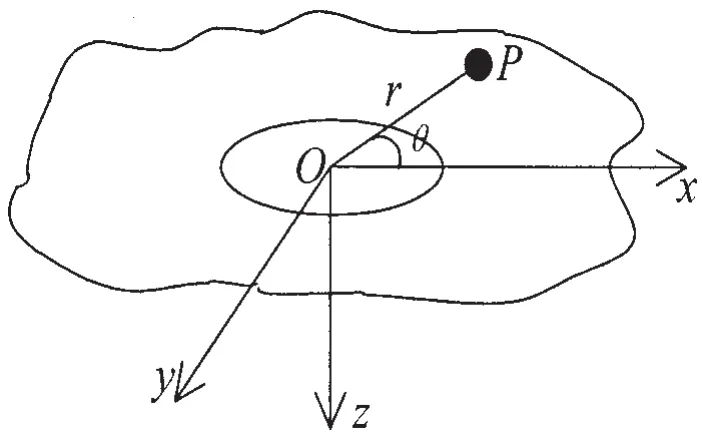
图1 含圆孔的薄板及其坐标系示意图Fig.1 Coordinate system of the thin plate with a circular hole

其中：w为z方向的位移，即挠度，ρ为平板的密度，h为板厚，D为弯曲刚度和μ分别为材料的杨氏模量和泊松比。

由于基于内部的圆孔建立坐标系，因此本文采用极坐标系求解该问题。如图1中平板上任意一点P，在平面直角坐标系下的坐标与极坐标系下坐标的关系为：

设挠度w具有如下形式：

其中：i为复数单位（i2=-1），ω为圆频率。代入（1）式即有：

Leissa[15]已求得极坐标系下（2）式的解为：

1.1 内边界条件

在薄板弯曲理论中，由弹性力学[16]可得圆板的转角φ、弯矩Mr、横向有效剪力Vr为：

若内边界固支，则满足：

以固支为例，将（3）式代入（5）式可得：

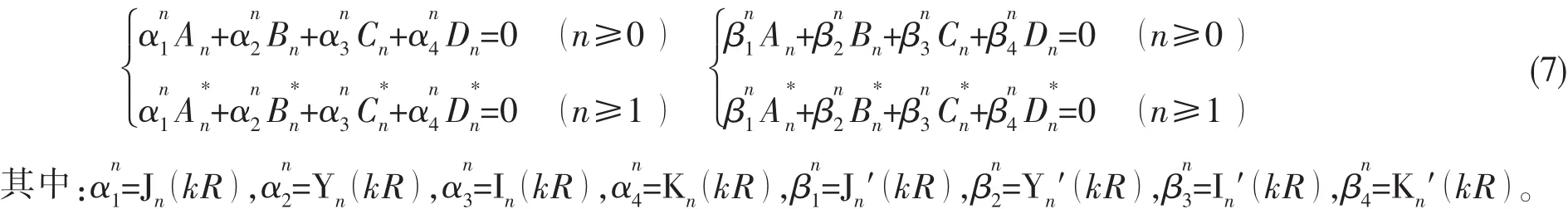
由（7）式可以求得：

对于三种边界情况，（8）式均成立，只是对应不同的边界情况，系数不同。

对于简支情况：

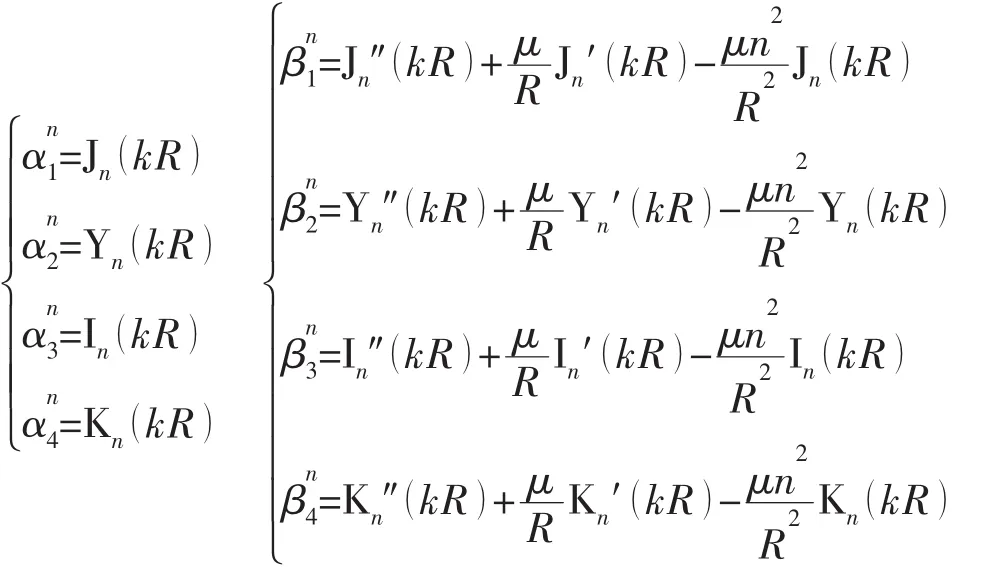
对于自由边界：

将（8）式代入（3）式，则挠度函数中未知量的个数减少，可以写为：

1.2 外边界条件

坐标系固定在圆孔中心位置，外边界的形状可任意，近似地用若干离散点取代外边界的连续曲线，使其各自满足对应位置的边界方程，从而使外边界条件近似满足。

如图2所示，P点为边界Г上的任意一点，对于曲线边界而言，三种边界条件分别表示为[17]：

自由，弯矩和有效剪力为零：（Vt）Γ=0，（Mt）Γ=0

其中：下标t表示P点所在位置的法线方向，m则表示切线方向。

图2 薄板外边界Fig.2 Outer boundary of the thin plate

图3 圆形外边界上取点Fig.3 Selected point of outer circular boundary

以外边界为圆形为例，如图3所示为一块含圆孔的圆形薄板，O点为圆孔的圆心，O′点为外圆板的圆心，考虑到圆形的轴对称性，以两圆心连线方向为x轴，O点为坐标原点建立坐标系，OO′的长度记为e，代表圆孔偏离圆板中心的距离，圆孔的半径为R。在外边界上取M个点使它们均满足边界条件，假设第i个点为P，其相对于坐标原点O的极坐标为（ri, θi），其相对于圆板圆心O′的极坐标为（r′ , θi′），显然r′为圆板的半径。对于P点，注意到P点的法线方向为，即圆板的半径方向。

若外边界固支，对于边界上任意一点P，应满足：

若外边界简支，则在P点有：

若外边界自由，则在P点有：

分别以O和O′为坐标原点建立的坐标系的坐标（r,θ）和（r′,θ′）之间的关系，根据偏微分的知识，可得：

且由图中的几何关系可得：

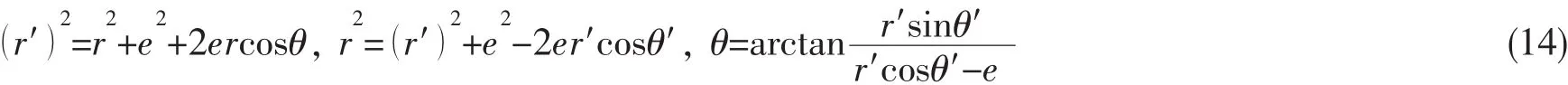
从而求得：

以固支为例，将以上结果代入（10）式则P点的边界条件如下所示，且对于边界上每个取点都需满足这两个方程：

再以矩形板为例，如图4所示，以圆孔的中心O为坐标原点，沿矩形板的长宽方向分别为x轴和y轴建立直角坐标系，矩形板的中心点为O′，其与O点的水平距离为e1，垂直距离为e2。矩形板的四条外边界分别记为l1，l2，l3，l4。设P点为在边界上取的第i个点，其直角坐标为（xi,yi），极坐标为（ri, θi）。

若P点在边界l1，l2上，则边界条件为：

若P点在边界l3，l4上，则边界条件为：

图4 矩形外边界上取点Fig.4 Selected point of outer rectangular boundary

其中：M，V为弯矩和剪力，分别可以由位移函数表示为：

其中涉及到的偏微分运算为：

而由极坐标与直角坐标的关系可知：

仍以固支为例，若P点在l2边界上，则满足的两个边界条件为：

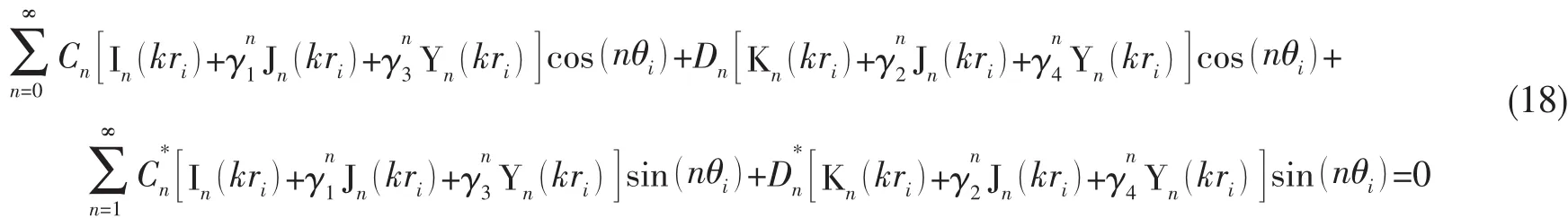
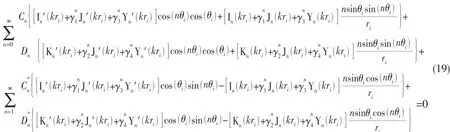
其他两种情况只需代入相应的边界条件即可，在此不作赘述。

2 求解分析

综合以上的分析，在（9）式中若取截断项数为N，则待定系数为：C，D，C，D，C*，D*，…，C，D，C*，

001111NNN D*N，共有（4N+2）个未知量。在外边界上取M个点，每个点满足各自的两个边界条件，则可得到2M个方程。最终获得的方程组表示为：

若2M=4N+2，即方程数与未知数个数相等，恰好能将未知数求解出，若2M＜4N+2，即方程个数少于未知数个数，所得解不唯一。若2M＞4N+2，即方程个数大于未知数个数，可以通过最小二乘法来求得唯一解。因此在选择截断项数和外边界上点数时，为确保求解的唯一性，应满足2M≥4N+2。

要由（20）式求自由振动固有频率只需使矩阵A的行列式为零，即由该方程求解得到的频率即为固有频率。但是首先矩阵A不一定为方阵，求解其行列式困难，因此可以转化为解，其中ATA为一个（4N+2）×（4N+2）的方阵。其次由边界方程可以看到，矩阵A中的项涉及贝塞尔函数，且表达式较复杂，并非关于频率的线性项，因此并不是一个线性方程，难以直接求得固有频率。参考文献中对非线性方程求根的做法[18]，转化为取值具体做法即是在频率域内循环，每个频率对应的行列式值的倒数取对数，当出现极大值时，认为该频率为固有频率的平方。

理论上，在边界上选择的点数越多，越能真实还原出边界的形状。截断项数越大，挠度函数越精确。实际上，M与N不可能取无限大，而且它们的取值关系到结果的准确性和运算的效率。为了确定M的取值，首先运用上述方法计算普通的不含圆孔的平板的自由振动频率。

表1和表2列出了Leissa在《Vibration of plates》一书中求解的周边固支圆板和周边固支正方形板的无量纲化自由振动固有频率与本文计算结果的对比。N为截断项数，M为外边界等距取点个数，括号内表示的是矩阵A的维数。由表1可见，N=3，M=8时，结果已经足够准确。而对于矩形板而言，因为有转角，形状比圆板更复杂，需要在边界上取更多的点以保证边界的形状（在此M均取为偶数以保证结构的对称性），因此相对应截断项数N也要取更大一些。表2中可见在N=5，M=12时，与N=4时的计算结果对比误差已经减小，而且在M=16时，由于A的维数差异较大，存在明显的漏频现象。由Hegarty等[8]和Ariman等[19]的研究可知，方程个数和边界取点个数有一定的比例，结果才更精确，而并非越大越好。由本文选取的算例可见，在本文的情况中方程数与未知量个数的比值大致为1时较为准确。因此为了运算的速度和结果准确性，N和M不需要再取得更大，在以下含圆孔的算例中，选取圆板参数N=3，M=8，选取矩形板参数N=5，M=12。

表1 周边固支的圆板的自由振动频率（无量纲参数=，泊松比0.3，a为圆板半径）Tab.1 Natural frequencies of clamped circular plate(Dimensionless frequencyPoisson’s ratio 0.3,radius a)

理论解（Leissa）[15]N=3 N=4 M=7（14×14）M=8（16×14）M=10（20×14）M=9（18×18）M=10（20×18）M=12（24×18）3.196 4.611 5.906 6.306 7.144 7.799 3.196 2 4.610 9 5.905 9 6.306 4 7.144 2 7.798 7 3.196 4.611 5.906 6.306 7.143 7.799 3.196 4.611 5.906 6.306 7.144 7.799 3.196 4.611 5.906 6.306 7.144 7.799 3.196 4.611 5.906 6.306 7.144 7.799 3.196 4.611 5.906 6.306 7.144 7.799

表2 周边固支的正方形板的自由振动频率（无量纲参数，泊松比 0.3，l为板宽）Tab.2 Natural frequencies of clamped square plate(Dimensionless frequencyPoisson’s ratio 0.3,edge length l)

理论解（Leissa）[15]（20×18） Error M=12 N=4 N=5 M=10（24×18） Error M=12（24×22） Error M=16（32×22） Error 5.924 5 8.538 1 10.366 8 11.473 4 12.844 8 14.503 4 14.809 5 5.927 8.248 10.564—12.779 13.952—0.04%-3.40%1.90%—-0.51%-3.8%—5.889—10.564 11.476——14.931-0.60%—1.90%0.02%——0.82%5.889 8.442 10.564 11.476 13.298 14.311 14.931-0.60%-1.13%1.90%0.02%3.53%-1.33%0.82%5.968——11.926 12.840——0.73%——3.94%-0.04%——

3 含孔平板算例分析

首先考虑含圆孔的圆板的振动问题。如图5所示，圆孔中心与圆板的中心距离为e，圆孔半径为b，圆板半径为a，显然应有b＜a，0≤e＜a-b，假设边界条件为外边界固支，内边界自由，计算无量纲化自由振动频率

若在圆板上含一个同心圆孔（e=0），即为一个圆环板的自由振动问题，则不同b/a比值下的结果与解析解的对比如表3所示。

表3 外周固支，内圆孔自由的圆环板自由振动频率 Tab.3 Dimensionless natural frequency，泊松比1/3of annular plate with clamped outer boundary and free inner boundary,Poisson’s ratio 1/3

阶数b/a=0.1 b/a=0.2 b/a=0.4 b/a=0.6 Leissa[15] 本文 Error（%） Leissa[15] 本文 Error（%） Leissa[15 本文 Error（%） Leissa[15 本文 Error（%）1 2 3 3.191 4.601 5.875 3.195 4.597 5.892 0.13-0.087 0.29 3.216 4.525 5.819 3.200 4.498 5.797 0.12-0.60-0.38 3.680 4.450 5.598 3.699 4.396 5.593 0.52-1.21-0.09 5.060 5.340 6.050 5.096 5.297 6.003 0.71 0.81 0.78

由表1可见，本文的计算结果与经典理论中的结果相比，误差小，基本一致，由此可验证本文理论的正确性和可行性。

图5 含偏心圆孔的圆板Fig.5 Circular plate with an inner eccentric circular hole

图6 不同孔洞尺寸下圆板基频随偏心距的变化Fig.6 The variation of fundamental frequency of circular plate with eccentricity under different hole sizes

当偏心距e不为零时，即圆孔相对圆板中心产生偏心。图6对比了五组不同的圆孔尺寸下，圆板的无量纲基频随偏心距的变化。显然可见，当内孔尺寸扩大，频率升高。随着偏心距的增大，基频均呈现降低趋势，孔径越大，偏心对于结构的影响就越大。如图7所示，本例计算含圆孔的正方形板，圆孔中心与矩形板中心x方向的距离为e1，y轴方向的距离为e2，圆孔半径为r，正方形板边长为L，显然 0≤e1＜L/2-r，0≤e2＜L/2-r，圆孔内边界自由，无量纲化频率取为

表4 含不同半径圆孔的四边固支正方形板前两阶频率，泊松比0.3Tab.4 The first two dimensionless natural frequenciesof clamped square plate with a central circular hole under different hole sizes,Poisson’s ratio 0.3

阶数2r/L 0 0.05 0.1 0.15 0.2 0.25 0.3 1 2 5.889 8.442 5.883 8.442 5.874 8.433 5.882 8.401 5.923 8.335 6.006 8.241 6.139 8.144

图7 含偏心圆孔的正方形板Fig.7 Square plate with an inner eccentric circular hole

图8 四边简支不同孔洞尺寸下方板基频随偏心距的变化Fig.8 Fundamental frequencies of simply-supported square plates with eccentricity under different hole sizes

首先考虑方形板正中含圆孔的问题，设e1=0，e2=0，计算了外边界四边固支情况下的固有频率，如表4所示。当圆孔不再位于板中心位置时，图8对比了在四边简支外边界下圆孔沿单方向偏心和沿对角线方向偏心的基频变化规律。

与圆板不同的是，由表4的数据可见，在四边固支的边界情况下，基频呈现先减小后增大的趋势，而第二阶频率则只有下降的趋势。而由图8可见，当孔径由2r/L=0.05变大为0.1时，固有频率略有下降，而变大至0.2时，又有明显提升，这与表4的结果是一致的。Hegarty等[8]认为这是由于开孔使应变能减少，及降低整板质量共同决定的，当质量减轻对固有频率的影响未超过能量对频率的影响时，固有频率就会降低，反之则会升高。此外，内孔仅沿一边偏心时固有频率变化幅度远小于内孔沿对角线方向偏心，尤其是在孔径较大或偏心距较大时，固有频率的下降非常明显。由此可知，具有较大开孔尺寸及较大偏心距的平板是较为不稳定的。

4 结论

本文基于经典薄板理论，结合数值计算方法，求解了含圆孔的薄板振动问题。坐标系建立于孔的中心，因此内边界方程能精确满足，通过对外边界上取点使其分别满足边界条件从而模拟外边界情况。与经典解析解的对比证明了本文方法是正确有效的，对于偏心孔洞的计算表明了孔洞偏心能使结构基频降低，且孔洞尺寸越大，其影响效果越显著。理论上本文的方法能够适用于计算多种规则孔洞和多种外边界形状，不过对于外边界点和待定系数的选取数量会直接影响计算效率，因此在计算其他形状的平板和孔洞时仍需进一步讨论和验证。