采用集中参数法的柔性衬里扩张室压力脉动衰减器滤波特性研究

杨 帆, 邓 斌

(西南交通大学 机械工程学院, 成都 610031)

随着液压系统向着高压、大流量、大功率方向发展，减振降噪逐渐成为一个迫切需要解决的问题，而压力脉动通常被认为是液压系统振动与噪声的主要来源[1]。当泵源、管路布局被限定的情况下，安装脉动衰减器衰减一定频率范围内的压力脉动，无疑是一种非常灵活有效的方法[2]。虽然压力脉动衰减器种类繁多，但大致可分为主动与被动两大类。被动式阻性结构中，采用软管代替液压钢管以及安装弹性管壁在液压系统中均有应用。针对软管、弹性管壁结构，国内外专家与学者都进行了大量的工作和研究[3]。Munjal等[4]对软管及管道壁泄漏噪声数学模型的有效性进行了实验验证；Yu等[5]发展了另一种软管数学模型；Johnston等[6]从实验的角度确定了软管材料的各向异性。除此之外，目前设计开发的一些加装衬里[7-9]、充气囊式衰减器结构[10-13]已陆续投放市场，但这些结构的测试实验数据还很少，并且用于预测脉动衰减性能的数学模型还无法完全建立。

除软管之外，加装柔性衬里也是一种灵活且有效的方式，Marek等认为这种方式具有以下优点：①柔性衬里比软管具有更大的容性，从而增加衰减器的插入损失；②在相同插入损失水平上，加装柔性衬里的衰减器整体结构尺寸会更小；③和软管相比，柔性衬里安装在衰减器壳体内部，并没有与外界环境接触，因此泄漏噪声的机率更低。Byrd等[14]利用脉动衰减器里安装柔性衬里来降低压力波的传播速度，设计了一种基于柔性衬里的H型脉动衰减器；Wheeler等[15]设计了一种可变阻抗层的压力脉动衰减器，并对其进行了滤波分析。本文研究了一种加装聚氨酯衬里的扩张室压力脉动衰减器，建立其等效电路的集中参数模型，并在研究频率范围内与分布参数模型做对比，验证了模型的正确性；采用老化和未老化两种聚氨酯材料，分析当液体静压力一定时，衬里材料成分对扩张室压力脉动衰减器脉动衰减性能的影响以及当材料成分不变，衰减器插入损失随液压静压力的变化。

1 集中参数模型建立

本文建立数学模型时，基于以下条件[16-19]：

(1)在脉动压力激励下，聚氨酯材料表现为均质、各向同性非晶态高聚物在小应变时的力学行为(即线性黏弹性)；

(2)脉动压力为小幅度信号(小扰动)，其马赫数很低，忽略液压油平均流的影响，信号为声学型；

(3)管路中的液压油为层流流动，没有切向速度分量；

(4)视液压油为理想流体，忽略黏性力、速度以及温度的轴向梯度影响；

(5)液压管路进出口边界条件具有轴对称性，周向模态不会被激发，本文研究频带范围小于平面波截止频率，高阶模态即使存在，也将按指数规律迅速衰减；

(6)液压管路中的脉动变化频率比较低，认为波幅仅是时间的函数而与空间位置无关。

填充聚氨酯柔性衬里的扩张室压力脉动衰减器结构模型如图1所示。衰减器进口位于x=0，出口位于x=l0。进出口液压管道半径为r。扩张室腔体内加装聚氨酯衬里，衬里内外半径分别为a,b，且聚氨酯材料长度为l0。

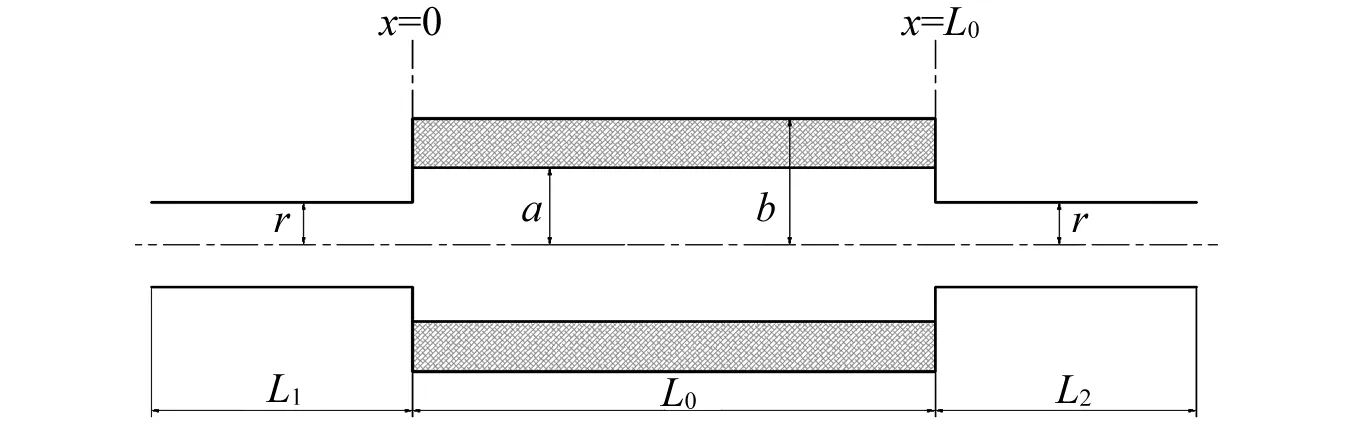
(l1=l2=74 mm,l0=175 mm,r=19.3 mm,b=34 mm,a=24 mm)图1 基于聚氨酯柔性衬里的扩张室压力脉动衰减器结构示意图Fig.1 Structural diagram of the expansion chamber hydraulic suppressor with a polyurethane compressible liner

对具有集中参数性质的流体系统，无须研究系统参数的连续变化情况，只须用若干个集中参数来描述它即可[18]。因此，建立图1所示脉动衰减器等效电路模型，如图2所示。

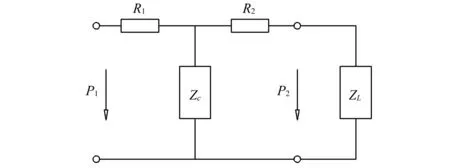
(a)

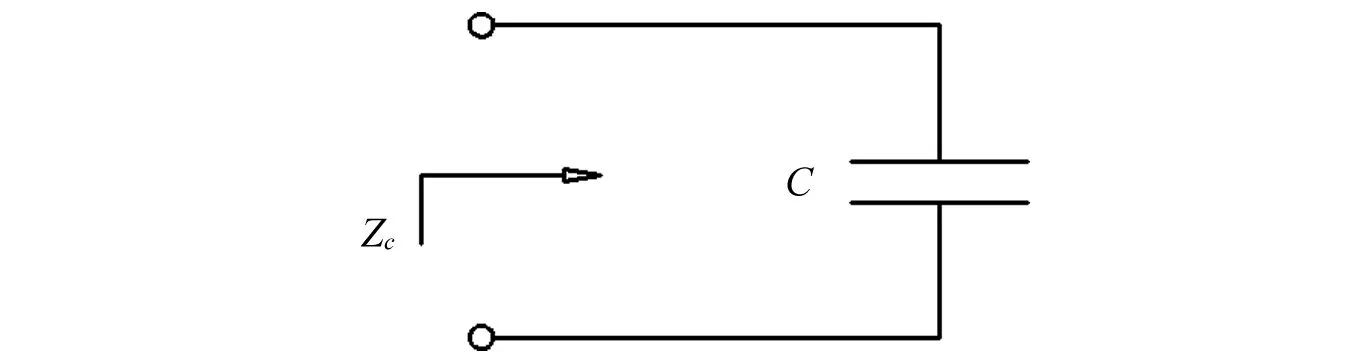
(b)图2 柔性衬里扩张室脉动衰减器等效电路模型Fig.2 Equivalent circuit model of the expansion chamber hydraulic suppressor with a compressible liner

图2中：R1,R2为管路动态流阻；Zc为扩张室等效阻抗；ZL为等效负载阻抗；C为等效流容。

扩张室结构的等效阻抗为

(1)

考虑容器壁弹性的组合体积弹性模量：

β=a2ρ

(2)

式中:a为液压管路中小扰动波的传播速度；ρ为流体密度。

聚氨酯衬里材料复模量表示为：

(3)

由于本文扩张室结构添加了柔性衬里，因此等效流容可以拆分成衬里和流体作用两部分流容的串联。

C=Cf+CL

(4)

(5)

(6)

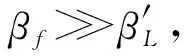
(7)

式中:Cf为液体流容；CL为衬里材料等效流容；βf为液体体积弹性模量；Vf为液体作用体积；VL为衬里材料所占体积。

2 集中参数流体四端网络

建立柔性衬里扩张室脉动衰减器液压消声系统流体网络模型，如图3、4所示。

图3 压力源表示的流体四端网络模型[16]Fig.3 The fluid four-terminal network model using pressure source

图4 速度源表示的流体四端网络模型[16]Fig.4 The fluid four-terminal network model using velocity source

当压力脉动源视为速度源时，认为Zn+1→∞，输出阻抗旁路近似为开路，得vn+1≈vn。将脉动源视为压力源时，认为Zn+1→0，对应于输出阻抗电路为短路，得到pn+1≈pn。根据线性网络理论[16,18]，得到流体网络传输方程：

pn+1=pn+Zn+1·vn

(8)

(9)

p0=Z0·v0

(10)

结合式(8)～(10)，得到柔性衬里扩张室压力脉动衰减器插入损失为[16]

(11)

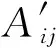
令声辐射阻抗等于流体管路特征阻抗：

(12)

式中:Y0为特征阻抗；Cf为脉动波传播速度；S为管道横截面积；ρf为流体密度。

本文研究频率范围为0～500 Hz，为了验证频带内集中参数建模的正确性，对无衬里扩张室结构分别进行集中参数和分布参数建模，采用图1几何尺寸，结果如图5所示。

图5 集中与分布参数模型结果对比Fig.5 Comparison of lumped and distribute parameter models

由图5可以看出，在500 Hz研究频带内，利用集中参数建模所得插入损失与分布参数建模结果吻合较好，证明了在该研究频率范围内，采用集中参数建模是可行的。随后，研究柔性衬里对扩张室压力脉动减器插入损失的影响，对三种结构：无衬里；衬里体积弹性模量为672 MPa；衬里体积弹性模量为15.97 MPa分别进行分析，结果如图6所示。

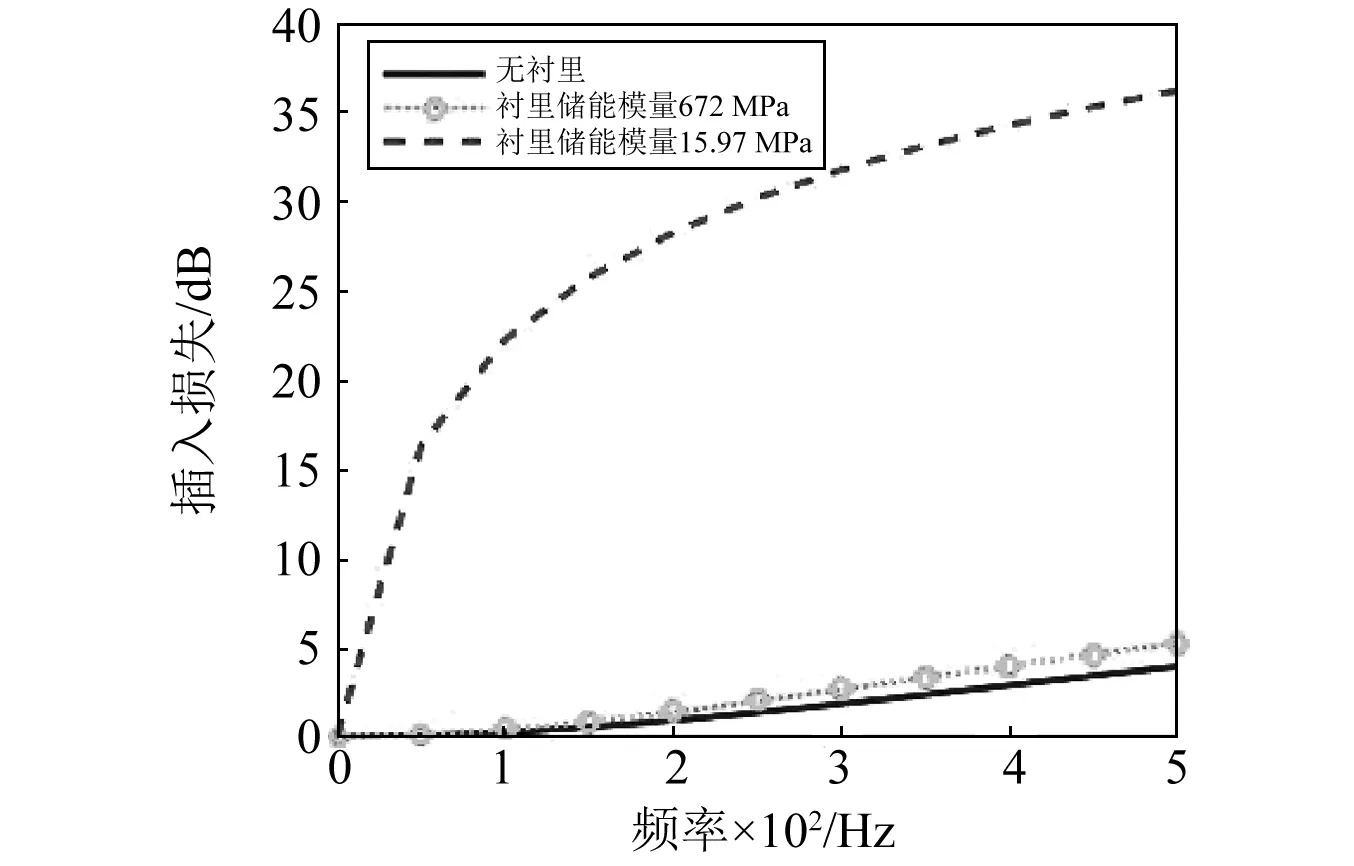
图6 衬里体积弹性模量对插入损失影响Fig.6 The effect of liner’s bulk modulus on insertion loss

由图6可知，当聚氨酯衬里材料储能体积弹性模量为15.97 MPa时，插入损失较衬里弹性模量672 MPa、无衬里结构得到明显提高。对扩张室压力脉动衰减器，假设Zn+1=Yn，Z0=Y1，Yn=Y1，得[19]：

(13)

式中:m为面积膨胀比；k为波数；Yn,Y1为上游、下游管道特征阻抗。

由式(13)结合图6可以得出，对于添加储能体积弹性模量为15.97 MPa的聚氨酯柔性材料做衬里时，可以大幅度减小扩张室的体积，有利于压力脉动衰减器的小型化与集成化。高聚物的损耗角正切，定义为[14,17]：

(14)

为了分析聚氨酯材料的损耗角正切对扩张室压力脉动衰减器插入损失的影响，由式(5)得：

(15)

(16)

研究这两种聚氨酯材料的损耗角正切对压力脉动衰减器插入损失的影响，如图7、8所示所示。

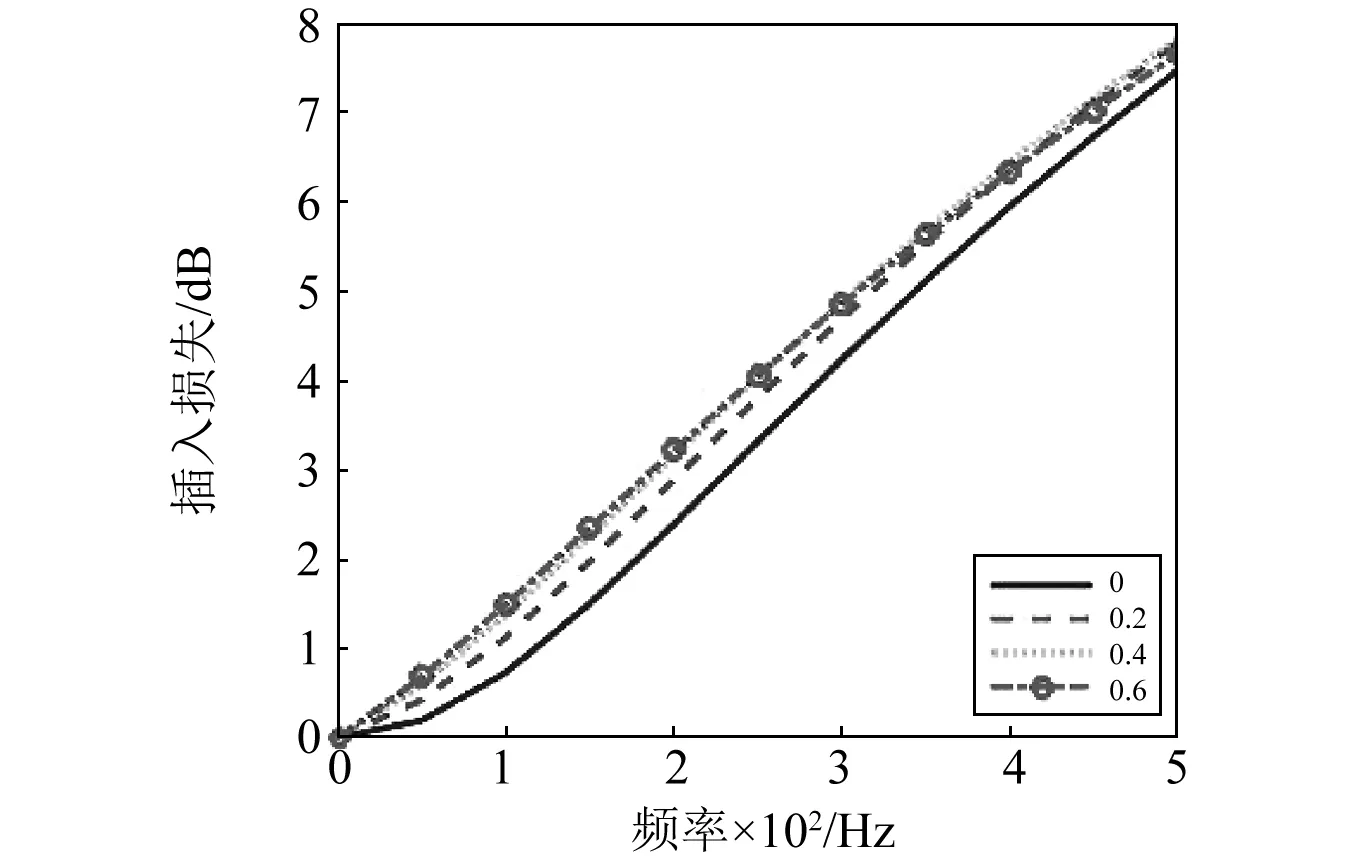
图7 损耗角正切对插入损失影响Fig.7 The effect of loss tangent on the insertion loss

图8 损耗角正切对插入损失影响Fig.8 The effect of loss tangent on the insertion loss

由图7、8可以看出，当聚氨酯材料储能体积弹性模量为672 MPa时，插入损失曲线随着损耗角正切的增大逐渐上移，且图7表明tanδ=0.4和tanδ=0.6两条曲线差异不大，即增大损耗角正切对扩张室压力脉动衰减器插入损失的影响有减缓的趋势；当储能体积弹性模量为15.97 MPa时，插入损失曲线随着损耗角正切的增大逐渐下移，并且曲线的走势大致相同。

3 实验分析与讨论

压力脉动测试平台以及扩张室压力脉动衰减器实验装置如图9、10所示。传感器采用西安微正电子科技有限公司生产的CYY28型脉动压力传感器，频响约10 kHz；变频器控制一个9柱塞斜轴式定量柱塞泵。

未安装柔性衬里的扩张室压力脉动衰减器理论插入损失(IL)与实验测量结果对比,如图11所示。

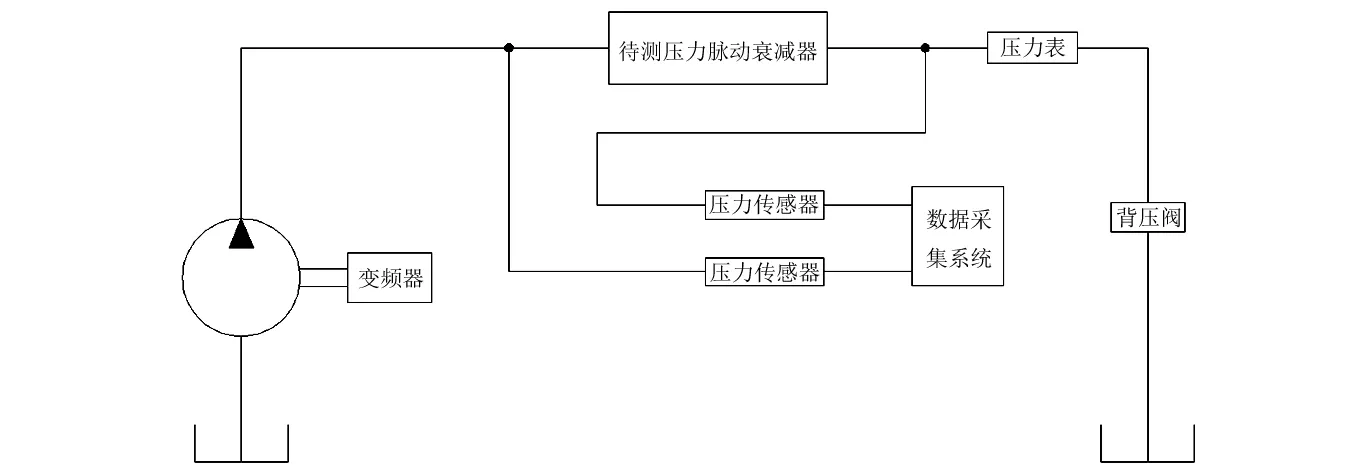
图9 压力脉动测试平台简图Fig.9 The schematic of the pressure pulsation test rig

1—扩张室腔体；2—内插管图10 扩张室压力脉动衰减器实验装置Fig.10 The experimental devices of the expansion chamber hydraulic suppressor

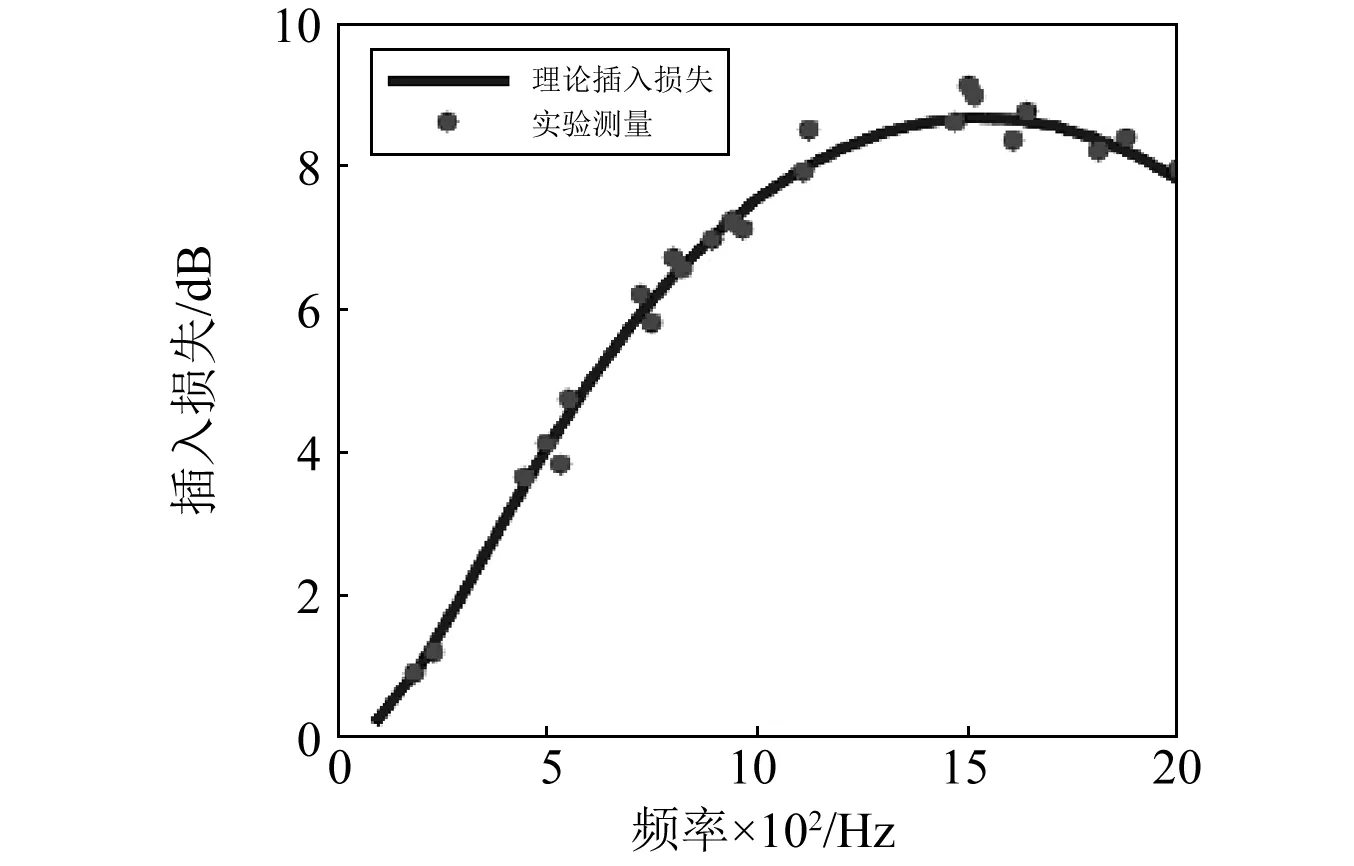
图11 理论插入损失与实验测量结果对比Fig.11 The comparison of the theoretical IL with the experimental measurements

由图11可以看出，在0～2 000 Hz研究频段内，未安装柔性衬里的扩张室压力脉动衰减器插入损失理论值与试验值吻合较好。Earnhart等[14]测得老化聚氨酯储能体积弹性模量和损耗角正切，如表1所示。

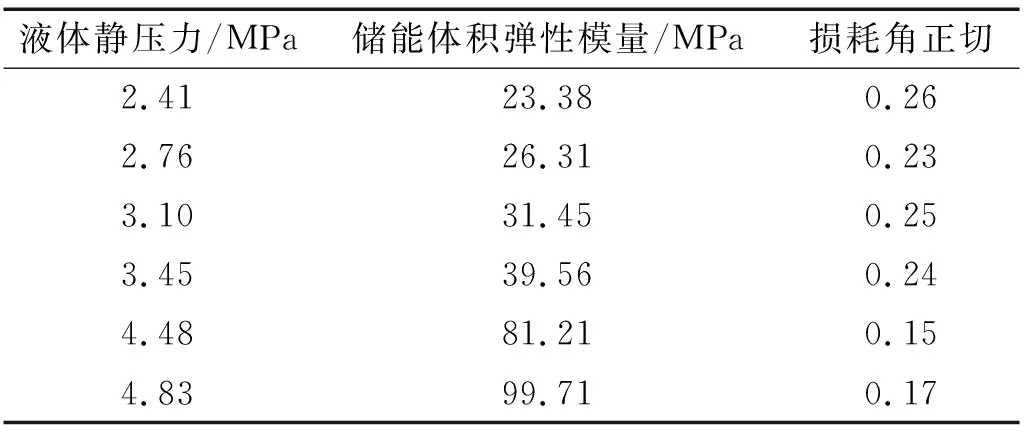
表1 老化聚氨酯储能模量与损耗角正切[14]Tab.1 Bulk modulus and loss tangent of voided polyurethane lining

由表1可以看出，随着液体静压力的增大，老化聚氨酯材料的储能体积弹性模量随之增大，即添加聚氨酯柔性衬里的扩张室脉动衰减器滤波特性与液压系统工作压力有关。当液体静压力分别稳定在2.76 MPa、3.45 MPa以及4.83 MPa，得到插入损失随脉动频率的变化曲线，如图12所示。

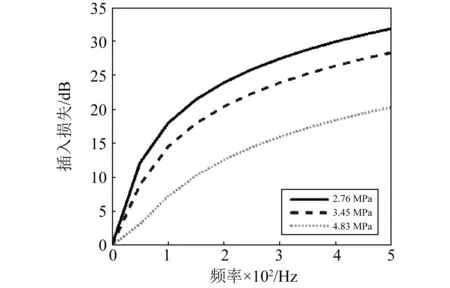
图12 不同压力下老化聚氨酯衬里对扩张室压力脉动衰减器理论插入损失的影响Fig.12 The effect of voided polyurethane lining to theoretical IL of expansion chamber hydraulic suppressor under different pressure

由图12可以看出，对同一种老化聚氨酯材料作为衬里的扩张室压力脉动衰减器而言，在不同工作压力工况下，会表现出不同的脉动衰减特性。Earnhart等的研究结果还表明，在液体静压力恒定工况下，改变聚氨酯材料内部声学结构会对衰减器滤波特性产生较大影响，其测得未老化聚氨酯材料储能体积弹性模量与损耗角正切，如表2所示。

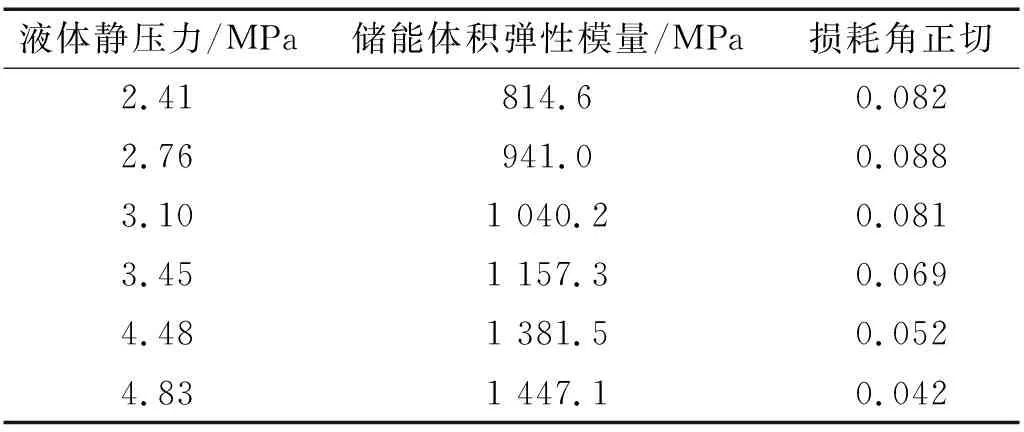
表2 未老化聚氨酯储能模量与损耗角正切[14]Tab.2 Bulk modulus and loss tangent of unvoided polyurethane lining

图13 不同压力下未老化聚氨酯衬里对扩张室压力脉动衰减器理论插入损失的影响Fig.13 The effect of unvoided polyurethane lining to theoretical IL of expansion chamber hydraulic suppressor under different pressure

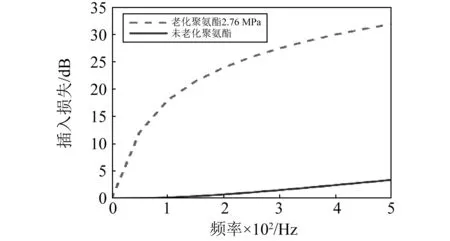
图14 两类聚氨酯衬里对理论插入损失影响(2.76 MPa)Fig.14 Influence of two kinds of polyurethane lining on the theoretical IL (2.76 MPa)

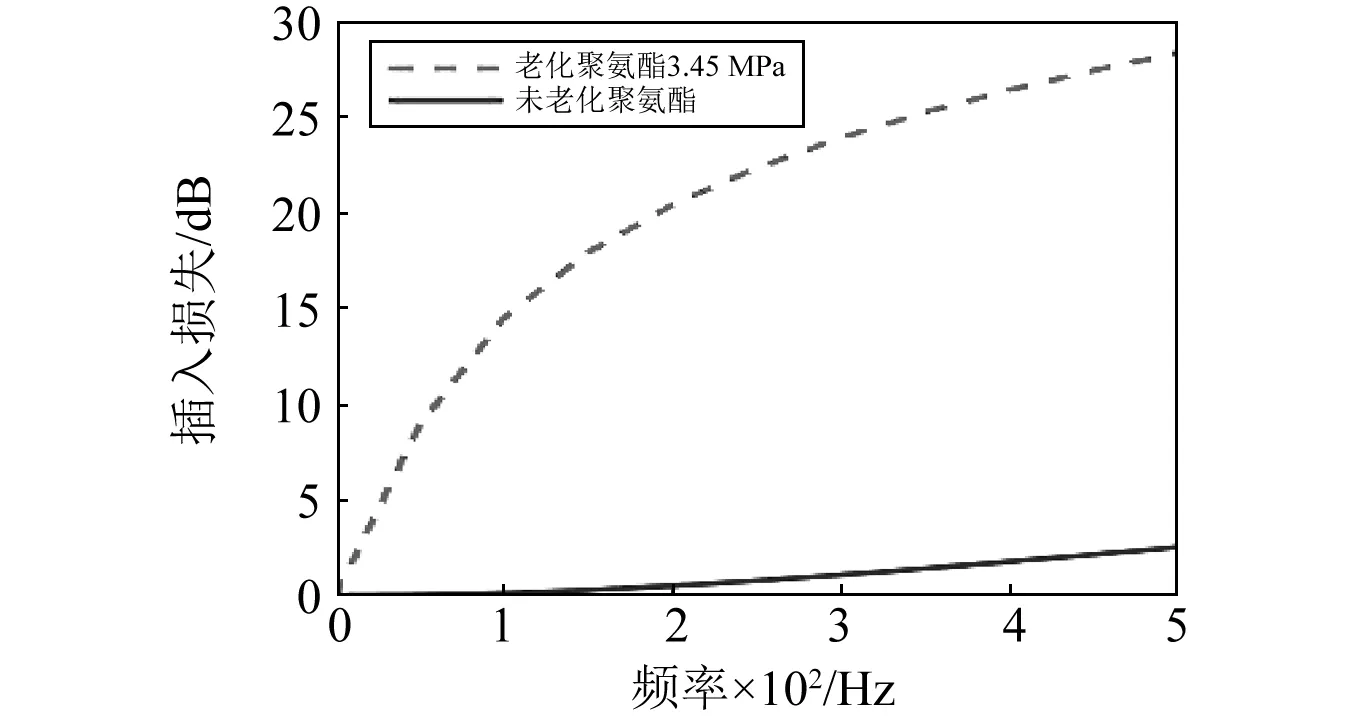
图15 两类聚氨酯衬里对理论插入损失影响(3.45 MPa)Fig.15 Influence of two kinds of polyurethane lining on the theoretical IL (3.45 MPa)

为了与老化聚氨酯材料做对比，仍然将系统压力定为2.76 MPa、3.45 MPa以及4.83 MPa，得到不同压力下未老化聚氨酯衬里对扩张室压力脉动衰减器理论插入损失的影响，如图13所示。

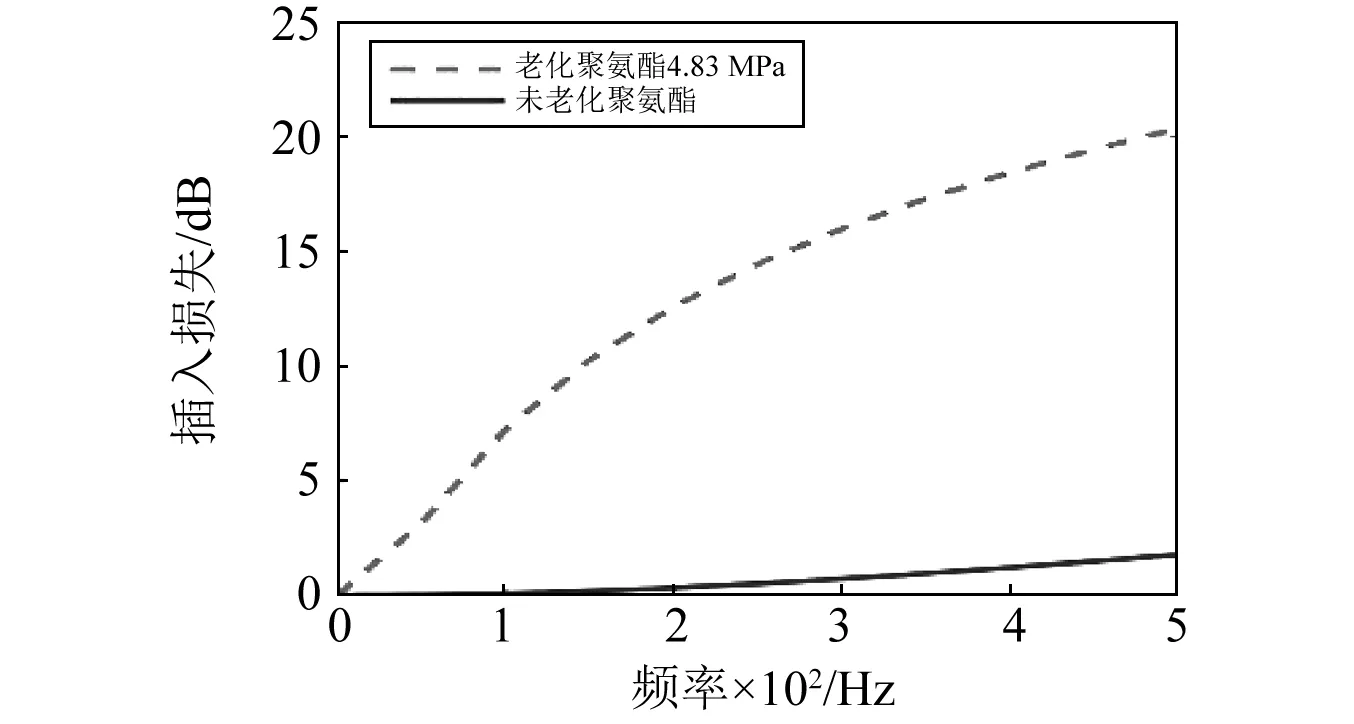
图16 两类聚氨酯衬里对理论插入损失影响(4.83 MPa)Fig.16 Influence of two kinds of polyurethane lining on the theoretical IL (4.83 MPa)

由图13～16可以看出，在一定液体静压力工况下，聚氨酯材料内部声学结构会对扩张室压力脉动衰减器插入损失产生较大影响。由于高聚物的内部结构可以进行人为控制，因此可以通过设计与选择合适的衬里材料性能以满足扩张室压力脉动衰减器不同的使用工况。

4 结 论

本文建立了聚氨酯柔性衬里扩张室压力脉动衰减器集中参数模型，计算结果表明：

(1)对同一种聚氨酯衬里材料而言，不同液体静压力工况下，具有不同的储能体积弹性模量和损耗角正切，会对扩张室压力脉动衰减器的插入损失产生影响。

(2)在液体静压力恒定工况下，老化与未老化聚氨酯衬里扩张室脉动衰减器具有不同的滤波特性，即高聚物衬里内部声学结构会影响衰减器的插入损失。

(3)与无衬里、未老化聚氨酯衬里相比，老化聚氨酯材料拓宽了衰减器的脉动衰减频带，有利于扩张室压力脉动衰减器的小型化与集成化。后期工作将集中于改变聚氨酯材料内部声学结构，研究其对扩张室脉动衰减器插入损失的影响，并逐步提高液体静压力等级，例如达到13～20 MPa。