舱内爆炸载荷下箱型梁结构提高舰船极限承载能力的研究

武少波， 张世联， 于海洋， 李 聪

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

现代海战中，半穿甲反舰导弹能够轻易地击穿舷侧板架，侵入并在舱内起爆，对舰船造成致命打击。因此，如何在舱内爆炸毁伤后，保证舰船具有更高的剩余总纵强度对于提高舰艇的生命力具有重要意义，因为它表征着船体在损伤状态下继续承受总纵弯曲载荷的能力，是维持船体生命力的基础。

国内已有一些研究[1-3]表明设置纵向箱型梁结构能够有效的提升船体在爆炸载荷作用下的剩余极限强度，这些成果均具有一定的指导意义。但上述研究都是基于外部爆炸工况来进行评估与分析，事实上，相同炸药量情况下舱室内部爆炸的破坏性要远大于外部爆炸，甲板结构变形损伤更大，将大大削弱船体结构的极限承载能力。另外，上述研究在进行与常规结构型式的比较时并没有考虑设置箱型梁所带来的结构重量增加问题。

为了探讨舱室内部爆炸载荷下纵向箱型梁结构的防护性能，本文选取常规结构和设置箱型梁结构舰船的完整舱段，借助MSC.DYTRAN软件分别进行舱内爆炸仿真计算，并将损伤结果作为初始大变形引入舱段剩余极限强度的计算中，通过分析两种结构的崩溃情况，为纵向箱型梁结构的抗爆机理作出解释。舱段剩余极限强度的计算采用准静态法[4]，借助ABAQUS软件进行。研究结果表明：在不增加结构横剖面积的前提下，箱型梁结构仍能显著提高舰船在舱内爆炸载荷下的剩余极限强度；在不同炸点位置的情况下，箱型梁结构对舱内爆炸载荷下剩余极限强度的提升效果是不同的。

1 舱段计算模型

1.1 计算模型的选取

纵向箱型梁防护结构运用的一个典型案例是德国的F124型护卫舰，该舰在强力甲板上设置3根纵向箱型梁结构。本文选取两个计算模型，一为常规结构舱段，另一为箱型梁结构舱段。其中箱型梁结构舱段参照德国F124型护卫舰设计，但布置形式作了变化，将中间箱型梁分成两根旁箱型梁分别布置在剖面中线两侧，位于舷侧的两个箱型梁被命名为舷侧箱型梁。常规结构舱段除01甲板外其他结构与箱型梁结构舱段基本相同。两种结构舱段的横剖面，如图1所示。

考虑到设置箱型梁会带来船体重量增加，为了能够比较，文中对常规结构舱段的01甲板做了适当的加厚，使两种结构舱段横剖面特征参数基本一致，如表1所示。

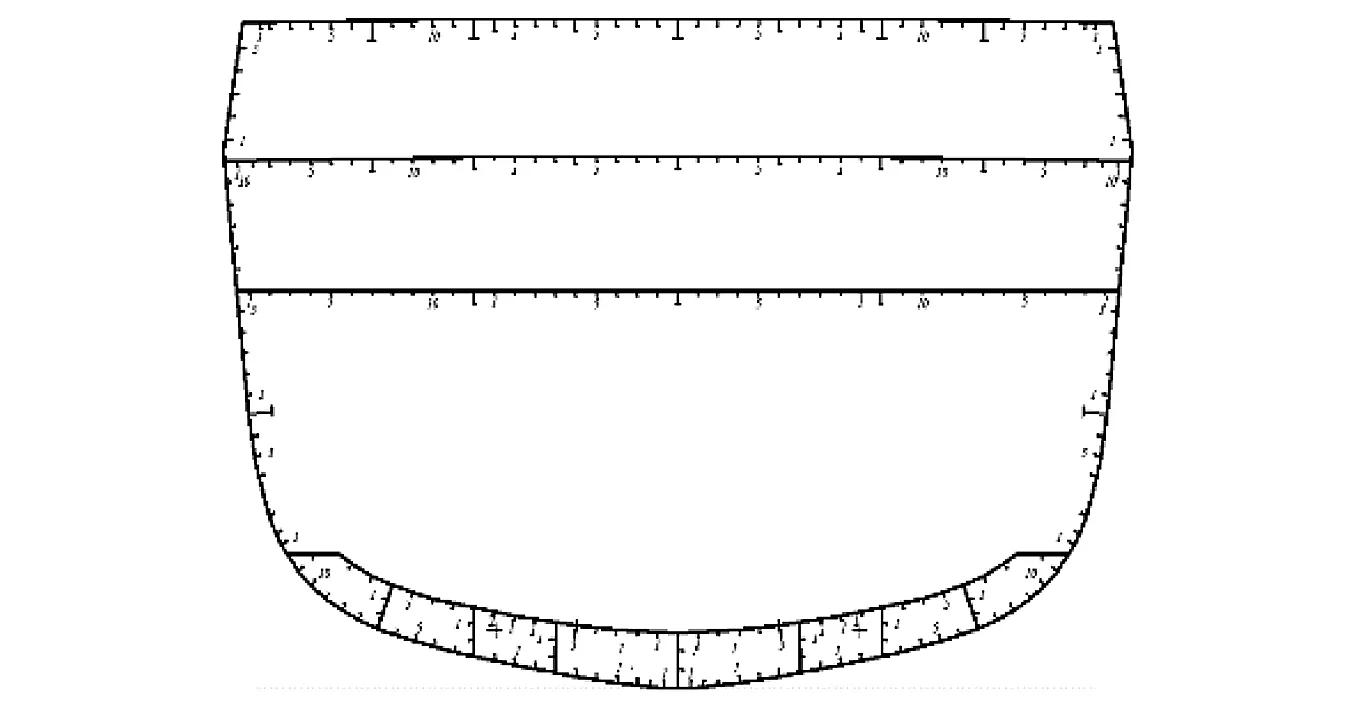
(a) 常规结构型式

(b)箱型梁结构型式图1 舱段横剖面剖面示意图Fig.1 Schemitic of hull structure section

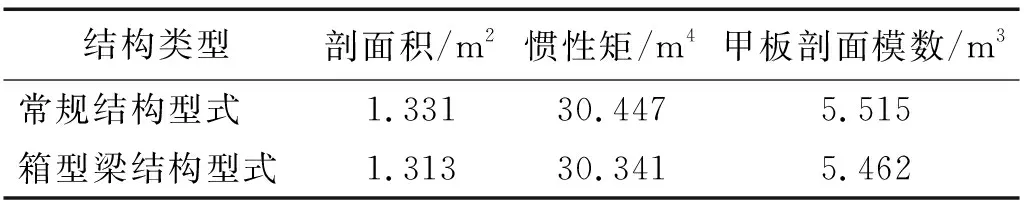
表1 舱段结构剖面特性表Tab.1 Section property of hull structure

1.2 本构关系和状态方程

结构材料的应力-应变关系近似的模拟为双线性弹塑性材料，弹性模量为2.07×105MPa，屈服极限为440 MPa，泊松比为0.3，硬化模量为4 GPa，失效应变为0.18。材料采用能考虑动态应变效应的Cowper-Symonds模型，同时考虑材料应变强化效应，其本构方程如下：

(1)

(2)

舱室内外空气采用理想气体状态方程描述，即Gamma方程：

p=(γ-1)ρe

(3)

式中：比热比γ=1.4、空气密度ρ=1.25 kg/m3、空气比内能e=2.1×105J/kg。

TNT炸药用高能高压的空气来模拟，同样采用Gamma方程，其中炸药密度取为正态分布随机变量，均值为ρd=1 630 kg/m3，炸药比内能ed=4.2×106J/kg。

1.3 计算工况的选择

舱内爆炸会给强力甲板带来显著的塑性变形，在船体承受中垂弯矩时，塑性变形将使甲板结构承受二次附加弯矩的作用，从而大幅降低结构所能承受的极限弯矩。纵向箱型梁的防护能力主要体现在其限制强力甲板变形的作用上。为了全面的衡量箱型梁对结构剩余极限强度的影响，本文选择不同的爆炸工况，对设置箱型梁舱段与常规结构舱段进行了数值仿真对比分析。

算例中共选取6个计算工况，工况汇总见表2；设置3个炸点位置，炸点位置分布如图2所示。炸点与01甲板的垂向距离均取为0.9 m。

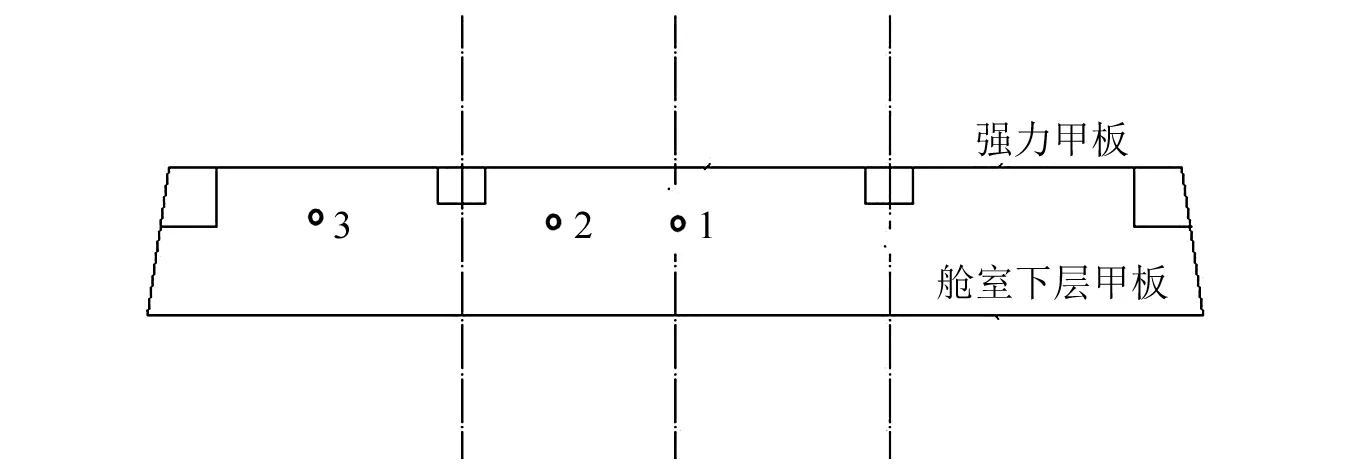
图2 炸点位置分布图Fig.2 Arrangement of explosion center

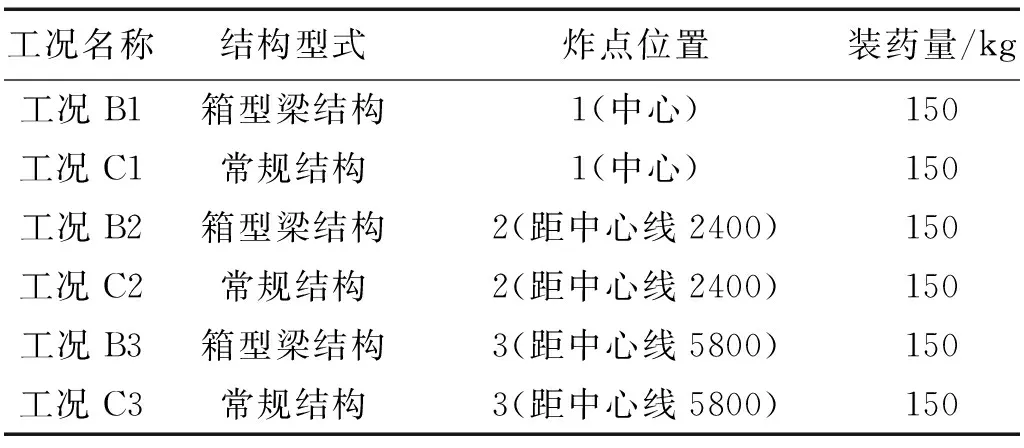
表2 计算工况汇总表Tab.2 Summaries of calculation load cases

设置舷侧两个炸点(位置2，3)是为了考虑舷侧爆炸对船体剩余极限承载能力的影响。表中各工况的数值模拟时间均取为0.2 s，以便能够得到舱段结构的稳定变形。

2 数值仿真计算

取上述两种结构的平行中体三舱段，分别建立有限元模型。利用MSC.DYTRAN软件中的流固耦合算法来模拟装药对舰船舱段结构的破坏作用，采用能够考虑耦合面破坏的快速耦合算法与Euler求解器求解。

本文中的剩余极限强度通过剩余极限弯矩值衡量。对于舱内爆炸，其引起的塑性大变形主要发生在01甲板，因此剩余极限强度计算主要针对使01甲板处于受压状态的中垂极限状态进行。将舱内爆炸数值仿真得到的塑性变形作为初始缺陷施加于舱段模型，利用ABUQUS软件中的Dynamic Explicit求解器，在模型两端设置多点约束，然后施加随时间平稳变化的强迫转角，记录端面形心处的弯矩转角曲线，通过准静态加载方式得到遭受舱内爆炸载荷作用后舱段的中垂极限弯矩。

为了对舱段爆炸前后的极限承载能力进行比较，还需计算舱段在完整状态下的初始极限强度。初始极限强度的计算使用Smith法，本文利用Mars2000软件分别计算常规结构和箱型梁结构型式危险剖面的完整极限强度。

3 数值仿真结果分析

3.1 强力甲板结构的塑性变形

仿真计算得到了6个计算工况下两种结构形式01甲板的变形图和变形云图。以计算工况B2和C2(表2)为例，其中间舱段01甲板的变形情况如图3所示。常规结构甲板变形的等值线呈矩形状由爆炸中心位置向外扩散，而箱型梁结构型式甲板则呈椭圆状向外扩散，这说明旁箱型梁对01甲板区域起到了有效的支持作用，从而限制了塑性变形的扩散。常规结构的01甲板变形几乎完全延伸到舷侧，而箱型梁结构靠近舷侧的甲板区域几乎没有变形，这是由于舷侧箱型梁对舷侧区域起到了有效的支持作用。工况B1、C1和工况B3、C3的01甲板变形具有类似的趋势。这说明设置纵向箱型梁可以有效的阻止01甲板塑性变形区域的扩散。

图3 计算工况B2、C2的强力甲板塑性变形情况Fig.3 01 deck plastic deformation pattern of cases B2 & C2

为了定量地比较01甲板的塑性变形情况，在所选舱段的01甲板上布置测点，测点1位于爆炸中心正上方，测点2位于旁箱型梁上方，测点3距离爆炸中心最远。计算结构在舱内爆炸载荷下的响应，分别输出结构在3个测点的垂向变形。

图4给出了计算工况为B1和C1时01甲板测点1和2处的垂向位移时历曲线，测点3处具有与测点2处类似的时历曲线。在位于爆炸中心正上方的测点1处，常规结构舱段的垂向位移略大于设置箱型梁结构舱段，这是因为对常规结构舱段的甲板厚度进行了调整，使得01甲板厚度大于设置箱型梁结构舱段。而对于测点2和测点3，虽然箱型梁结构舱段01甲板板厚较薄，但其垂向位移仍然比常规结构小90～150 mm，说明在横剖面面积大致相同的情况下，设置纵向箱型梁结构能有效的较小01甲板的塑性变形值。工况B1、C1和工况B3、C3的垂向位移时历曲线具有类似的性质。

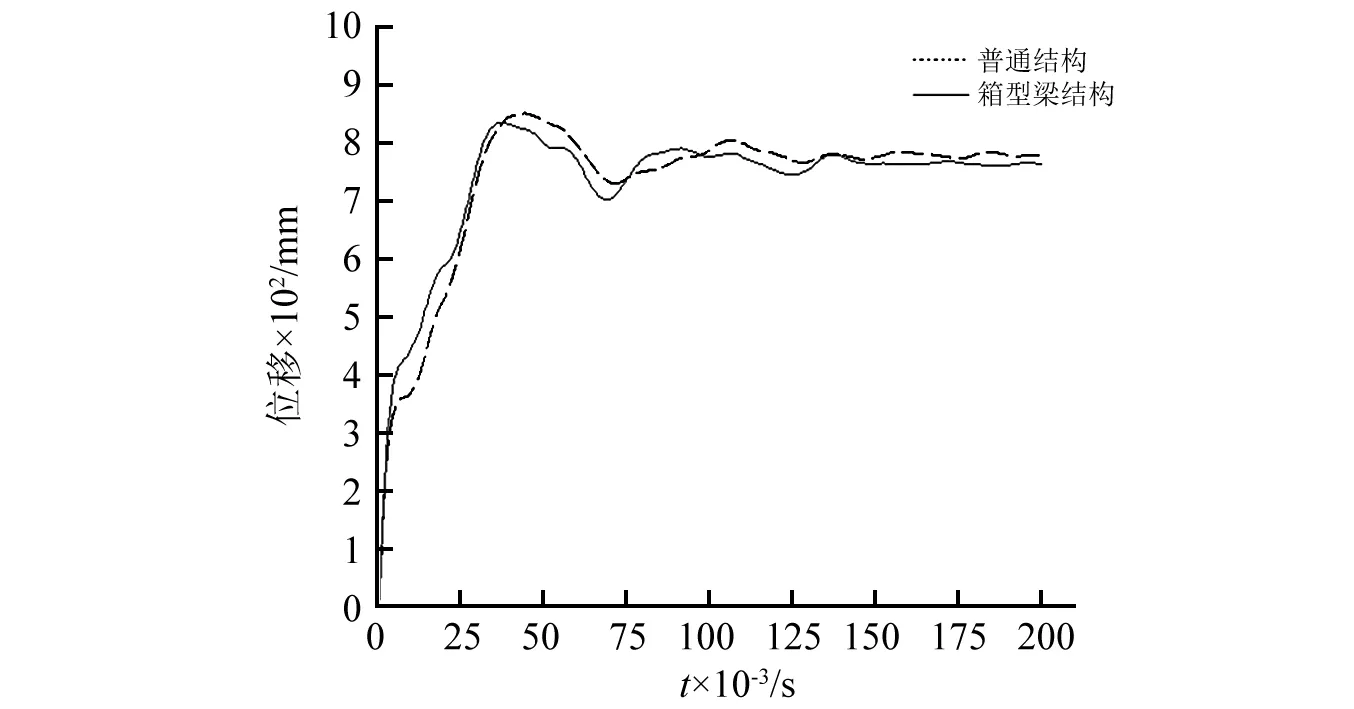
(a)测点1

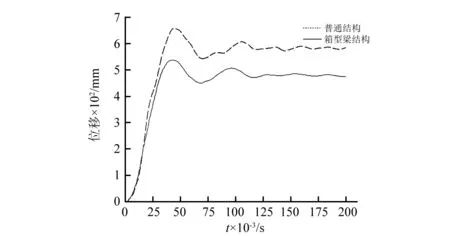
(b)测点2图4 计算工况B1、C1的测点位移时历曲线Fig.4 Deformation-time history of cases B1 & C1 at measuring point 1 & 2

分析结果表明：在不增加横剖面剖面积的前提下，纵向箱型梁结构能够对甲板板架和舷侧板架提供有力的支撑和约束，从而有效的阻止塑性变形区域的扩散，明显减小强力甲板塑性变形值。

3.2 舱段的剩余极限强度

利用Mars2000软件分别计算常规结构和箱型梁结构舱段危险剖面的完整极限强度，得到弯矩-转角曲线如图5所示。常规结构型式和箱型梁结构型式在完整状态下的中垂极限弯矩分别为2.20×106kN·m和2.06×106kN·m。

(a) 常规结构型式

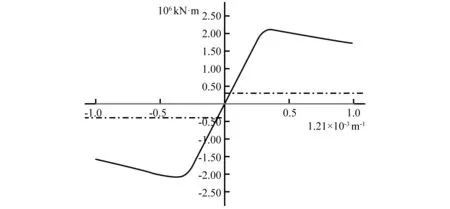
(b) 箱型梁结构型式图5 完整状态下剖面弯矩转角曲线Fig.5 Moment-rotation angle curve of section under complete state

仿真计算得到了6个计算工况下两种结构型式极限状态时的应力分布云图。以计算工况B2、C2和B3、C3为例，其应力分布云图如图6所示。可以看出，当结构处于极限状态时，箱型梁结构舱段01甲板的屈服区域大于普通结构舱段，说明箱型梁结构01甲板的可承载区域大于常规结构，这是因为箱型梁结构01甲板的塑性变形区域小于常规结构。另外，位于炸点一侧的01甲屈服区域小于另一侧，这是因为舷侧爆炸使强力甲板的塑性变形区域呈现非对称分布。

将剩余极限强度仿真计算得到的结果与计算得到的初始极限强度数据进行比较，可以定量地描述箱型梁结构提高舱内爆炸载荷下舰船剩余极限强度的效果以及在不同舱内爆炸工况下箱型梁结构对剩余极限强度的贡献。比较结果如表3所示。

图6 两种结构型式中垂极限状态应力分布云图Fig.6 Stress nephogram of two structure types under sagging ultimate state

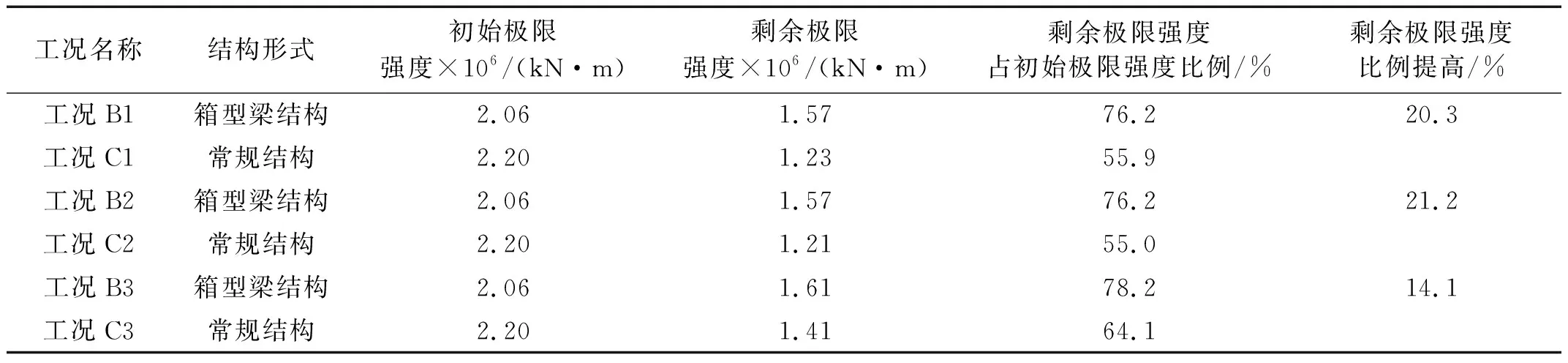
表3 剩余极限强度计算汇总表Tab.3 Summaries of remaining ultimate strength calculation

由表3中数据可知，在各组计算工况下设置箱型梁结构舱段的剩余极限强度无论在数值上还是所占比例上都较普通结构舱段有显著提高。在本文的设计中，箱型梁结构型式与常规结构型式有着大致相同的剖面积，这说明在不增加结构横剖面积的前提下，纵向箱型梁结构仍能够较为显著的提高船体的剩余极限强度。同时注意到，工况B1和工况B2中箱型梁结构型式的剩余极限强度所占比例的提高都达到了20%以上，而在工况B3中为14.1%，这是因为该工况的炸点位置靠近舷侧，内部爆炸对常规结构型式强力甲板所造成的整体塑性变形小于其他两个炸点位置，极限强度的损失也相应减少，因此纵向箱型梁的作用被一定程度的弱化。

图7给出了不同炸点位置的极限强度曲线。对于常规结构型式，舱内中心爆炸(工况C1)和近中心爆炸(工况C2)曲线的变化趋势基本一致，曲线峰值则明显低于舷侧爆炸(工况C3)，这说明就船体剩余极限强度指标而言，舱内中心区域爆炸比舷侧爆炸更加危险，原因在于靠近中心区域的爆炸会引起甲板结构的整体塑性大变形，而舷侧爆炸带来的是局部非对称的塑性变形。但对于箱型梁结构型式，三个炸点位置(工况B1、工况B2和工况B3)对应的极限强度曲线峰值基本上相同，舷侧爆炸(工况B3)略高于靠近中心区域的两个炸点位置(工况B1和工况B2)。究其原因，强力甲板上设置的旁箱型梁和舷侧箱型梁结构能对甲板结构起到了有效的支持作用，总可以将甲板的塑性变形区域有效的控制在两根箱型梁之间，因此爆炸位置对箱型梁结构型式舱段的剩余极限强度影响不大。

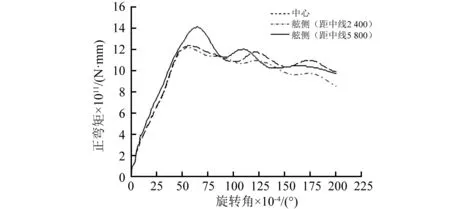
(a) 常规结构型式

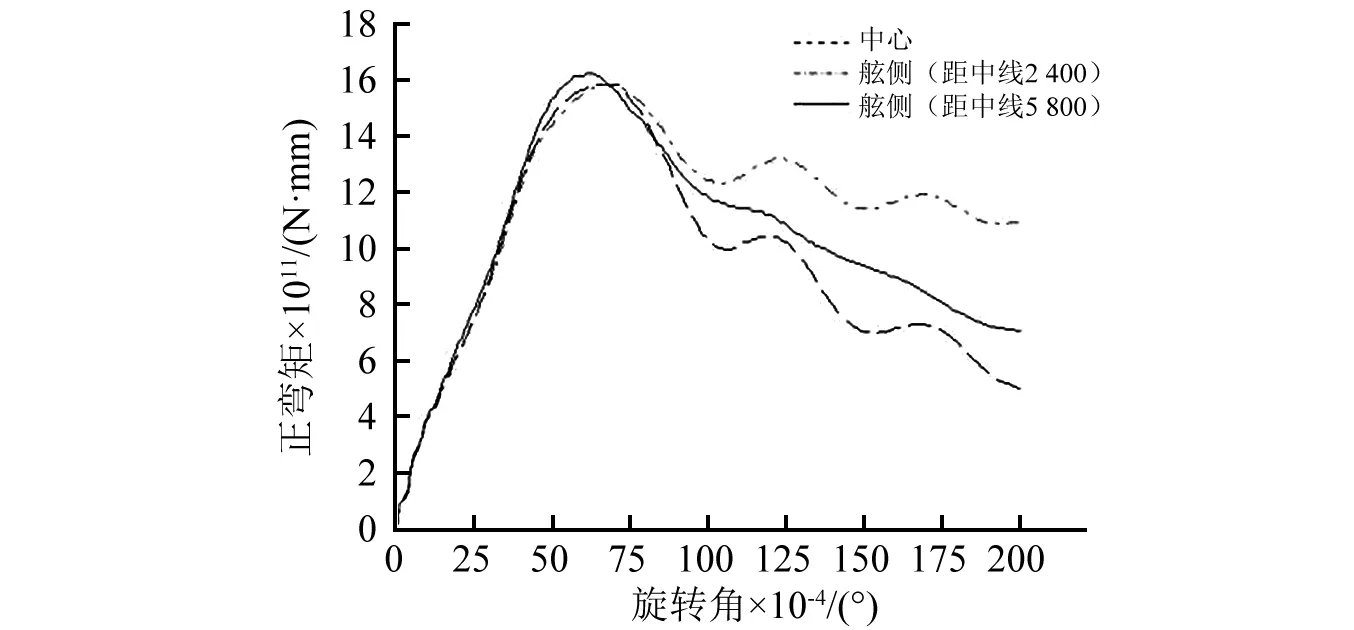
(b) 箱型梁结构型式图7 不同炸点位置的极限强度曲线Fig.7 Moment-rotation angle curves of different explosion positions

4 结 论

本文考虑设置箱型梁结构所引起的重量增加以及不同炸点位置的影响，对舱内爆炸载荷作用下纵向箱型梁结构提高舰船剩余极限强度的效果和机理进行了研究，得到如下结论：

(1)纵向箱型梁结构能够有效的抑制塑性变形区域的扩散，从而使甲板结构拥有更大的有效承载区域，因此设置纵向箱型梁结构可以大幅提升舰船在舱内爆炸载荷下的极限承载能力，在不增加结构横剖面积的情况下，舱内中心区域爆炸工况下的提高比例可以到达20%以上；

(2)炸点位置靠近舷侧的舱内爆炸所造成的强力甲板整体塑性变形比其他情况要小，在此情况下，纵向箱型梁结构提高舰船舱内爆炸载荷下剩余极限强度的作用被一定程度地弱化，但提高比例仍可高达14%；

(3)以剩余极限强度为衡准，对于常规结构舰船而言，舱内中心区域的爆炸将比舷侧爆炸更加危险；而对于设置箱型梁结构舰船而言，由于几乎总是能够将强力甲板的塑性变形区域有效的控制在两根箱型梁之间，舱内爆炸位置对剩余极限强度的影响不大。

非线性有限元方法虽然可以很好的求解具有初始缺陷结构物的剩余极限强度，但初始缺陷的确定却十分复杂，本文中仅考虑了舱内爆炸作用后产生的结构变形。在实际情况下，内部爆炸造成结构变形损伤的同时必然伴随有残余应力和应变的产生，另外，瞬时高温的作用也会导致材料性能的改变。上述因素都会对结构的剩余极限强度产生影响，因此需要进一步的研究。