船用新型多层负刚度冲击隔离器性能分析

任晨辉， 杨德庆

(高新船舶与深海开发装备协同创新中心；海洋工程国家重点实验室；上海交通大学 船舶海洋与建筑工程学院，上海 200240)

内部设备的抗冲击防护作为舰艇在水下爆炸环境中强度和生命力的薄弱环节正受到广泛的关注。设备抗冲击的关键在于连接船体与设备的冲击阻隔装置，这类装置既要承受设备自重(静载荷)，也要在极端冲击载荷作用下起到保护设备的作用。冲击载荷作用时间短，能量集中，造成的破坏大，这类载荷包括：水中非接触性爆炸、接触性爆炸以及炸弹在空中爆炸或舰船自己的武器发射所产生的气浪等[1-3]。在研究冲击响应的众多方法中，实船爆炸试验与模型冲击机试验最接近实际，但试验成本较高，对环境要求严格，而数值仿真作为一种新的可重复的有效评估手段，已在结构设计领域发挥了巨大作用。因此，通过冲击加速度的数值仿真分析可以评价结构的抗冲击能力并为结构的设计提供依据，具有重要的现实意义。

现有的船用设备一般采用隔振器进行抗冲击防护，性能有限，而高性能抗冲击防护装置涉及主动控制，制造及维护成本高。本文考虑新的设计理念，将新型超材料与结构应用于抗冲击结构的开发中。

负刚度构件由于其静力不稳定性，很少单独使用，而是与正刚度部件并联形成准零刚度结构，用于超低频段结构减振[4]。其中预成型(pre-fabricated)余弦曲梁在一定条件下具有双稳态特性，易于加工，可作为微开关、微继电器/接触器等，在MEMS(微机电系统)及惯性控制中应用广泛[5]。在材料领域，Correa等[6]提出了一种基于SLS(选择性激光烧结)成型技术的新型负刚度蜂窝超材料，并将其受压变形时的力学性能与常规蜂窝进行了比较，证明其相对于常规蜂窝有较好的能量吸收能力，但在船舶与海洋工程领域尚未见其应用。

本文在研究余弦梁负刚度特性的基础上，提出将多层负刚度余弦梁结构用于船舶设备的冲击防护。其设计思路是：在爆炸等极端载荷下，冲击首先作用于船体板架，之后在传递给设备前先经过多层负刚度冲击隔离系统，能量转化为隔离系统的内部应变能，起到保护设备的作用。本文通过研究单双曲梁的力学特性，考虑设计结构的尺寸和轮廓限制，建立数学优化模型，确定多层负刚度余弦梁结构的参数，建立完整系统的有限元模型。然后，基于前联邦德国国防军舰建造规范BV043/85，将三折线冲击谱转化为双正弦波加速度时间历程施加于船体板架。最后，利用有限元软件ABAQUS进行动力分析，得到设备的位移、速度、加速度响应，评估抗冲击性能。

1 并联余弦梁的负刚度特性

如图1和2所示余弦梁，其尺寸参数包括：梁两约束端的距离l、梁截面厚度t、梁截面宽度b、初始时刻梁轴线中点距两端点连线的垂直距离h等。在跨中受到垂直向下的作用力f时，根据梁几何特性的不同，f的大小与梁中点位移d的关系可分为三种情况：

(1) 当Q=h/t比较小，下压过程中，轴力小于阶屈曲力时(对于限制二阶屈曲模态的梁，i取3；不限制二阶屈曲模态时，i取2)，垂向力与跨中位移的关系为f1=f1(d)。

(2) 当不限制梁的二阶屈曲模态时，若Q=h/t比较大，下压过程中，轴力会达到梁二阶屈曲力，垂向力与跨中位移的关系为f2=f2(d)。

(3) 当限制梁的二阶屈曲模态时，若Q=h/t比较大，下压过程中，轴力会达到梁三阶屈曲力，垂向力与跨中位移的关系为f3=f3(d)。

图1 跨中受压的预成型余弦梁示意图Fig.1 Schematic diagram of prefabricated cosine beam under lateral force at midpoint

图2 余弦梁前三阶屈曲模态及限制二阶模态时的变形过程Fig.2 First three buckling modes and configurations of displacement under lateral force at midpoint with second mode constrained

Qiu等[7]引入无量纲量Fi=fil3/EIh(i=1,2,3)、 Δ=d/h、Q=h/t对这三种力-位移关系进行了推导，得到无量纲的力Fi(i=1,2,3)如下式

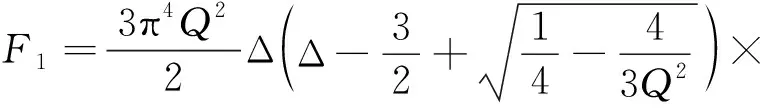
(1)

原公式中关于F2的系数有误，本文重新推导并得到其有量纲形式fi(i=1,2,3)，用于建立理论优化模型。

(2)

(3)

式(2)对应的无量纲形式为

(4)

按式(4)作图表示这三种力-位移关系如图3。

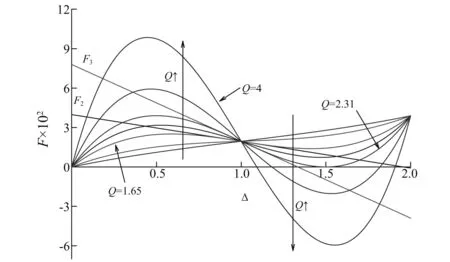
图3 不同几何特性的余弦梁力-位移关系Fig.3 Different solutions of normalized force-displacement relationship for pre-fabricated cosine beam

从图3中可以看出，无论哪种情况，随着位移的增加，力的值总是先增加到最大(该峰值称为正向屈曲力)，随后位移增加力减小出现所谓“负刚度”区域，最后力从最小值开始随着位移的增加而增加。此外，Q=1.65时，F1与F2相切；Q=2.31时，F1与F3相切， 且与x轴相切， 即Q>2.31时，作用力的最小值将为负，即出现所谓“双稳态”特性。

为保证多层余弦梁结构作为抗冲击支座的初始刚度与变形过程中的侧向稳定性，必须限制梁的二阶屈曲。一种方法就是将两相同的余弦梁在中部和两端固结[8]，如图4所示。

图4 单余弦梁与并联双余弦梁Fig.4 Single cosine beam and centrally-clamped cosine beam

2 多层负刚度抗冲击隔离器的设计与优化

Correa等[9]提出了一种新型负刚度蜂窝材料，将双曲梁按一定形式排布成蜂窝的形状，如图5(a)所示。本文考虑不同的梁尺寸参数、双曲梁排列的层数、列数，提出一种多层负刚度冲击隔离装置，用于在极端冲击载荷下船舶设备的保护，如图5(b)所示。由于要限制曲梁两端的横向位移，在两端板的中点处加装水平厚板，提供约束。

本文冲击隔离器的制造材料采用ABS树脂，其材料弹性模量1 800 MPa，泊松比0.389 7，密度1 040 kg/m3，屈服强度为50 MPa。这类材料的屈服极限与弹性模量之比较大，适合用于负刚度梁等大应变结构，同时可用3D打印等加工技术一体成型，规避了金属材料焊接缺陷与残余应力等问题。

图5 负刚度蜂窝材料与多层负刚度抗冲击器Fig.5 Negative stiffness honeycomb material and multilayer negative stiffness shock isolator

以构成抗冲器的单余弦梁尺寸参数h，l，t，D作为设计变量， 以正向屈曲力Fb为目标函数， 约束条件为梁最大应力σmax不超过材料屈服极限σy的80%， 以及模型的整体尺寸限制。另外，为保证梁正向屈曲后能够返回其原始稳态(这要求Q<2.31)， 且避免回复力过小，设置Q<2.2。最终建立的抗冲器尺寸优化模型的数学列式如式(5)

(5)

式中：D表示抗冲击结构的纵向长度， width、height分别表示模型整体宽度和高度，其余参数见图1。

根据对称性，初步计算取四层双余弦梁模型，层数对抗冲击性能的影响将在第3节中研究。取列数从1到4变化，分别进行优化，如图6所示，根据最大正向屈曲力的值选择作为最终优化结果，如表1所示。

图6 具有不同列数双余弦梁的多层负刚度抗冲击结构横截面Fig.6 Negative stiffness shock isolators with different columns of centrally-clamped cosine beams

表1 优化结果Tab.1 Optimization results

为将有限元分析与公式(2)解析解结果比较，按表1中参数建立有限元计算模型，利用riks弧长算法考虑几何非线性进行力-位移关系分析，变形过程如图7。为节省分析时间，只研究单余弦梁，且单梁纵向长度取D/10=30 mm。

图7 余弦梁受压不同时刻的挠曲变形Fig.7 Deflection of a cosine beam in various stages of lateral compression

单余弦梁变形过程中的跨中力-位移关系如图8，正向屈曲力与最大正应力，如表2所示。

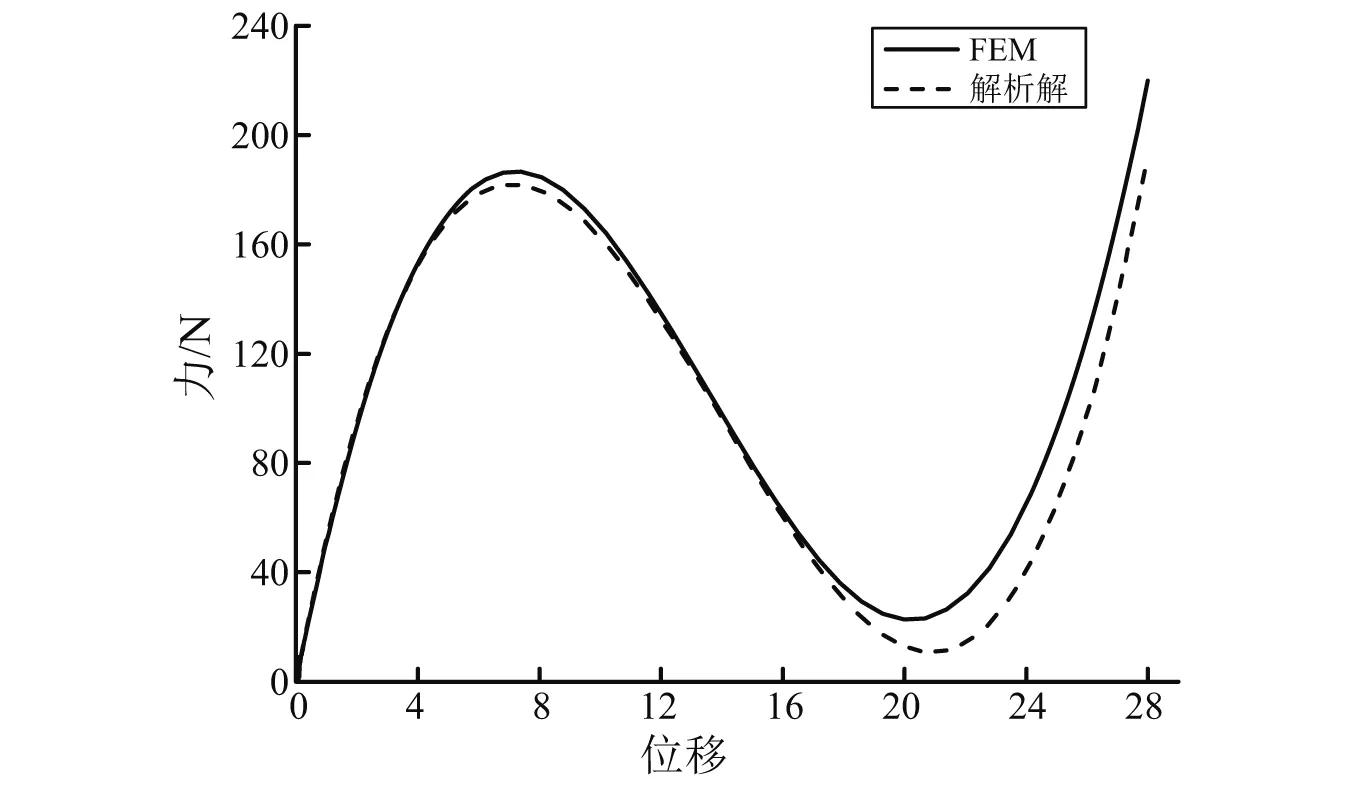
图8 几何尺寸优化后的跨中受压余弦梁力-位移关系Fig.8 Force-displacement relationship of a cosine beam under lateral force at midpoint with dimensions in Tab.1

表2 单余弦梁有限元分析结果与公式解Tab.2 FEA and analytic results of a single cosine beam

从图8和表2结果可以看出，有限元解与式(2)结果非常接近，误差的出现可能是由于FEA模型的加载区域具有一定宽度，与理论公式在中点加载有差异。根据有限元分析结果，考虑四层双余弦梁串联，设计的多层负刚度冲击隔离器(表1)的最大正向屈曲力应为186.66×2×10=3 733.2 N，与表1的结果误差很小。

3 船用新型多层负刚度隔离器的抗冲击性能

按照表1优化结果设计出船用多层双余弦梁负刚度冲击隔离器，并装配到验证船体板架上[10]。冲击隔离器结构使用六面体单元网格，板架采用四边形板单元网格，设备重量200 kg，重心距结构上表面400 mm。板架长1 800 mm，宽1 000 mm，板厚6 mm，板架纵骨用T型材T50×50×5×5，肋骨用等边角钢L30×3，扶强材用T型材T25×25×3×3，板架材料为屈服强度390 MPa高强度钢，材料弹性模量210 GPa，泊松比0.3，密度7 800 kg/m3，抗冲击结构材料为ABS树脂。板架四周简支。具有4层双曲梁的模型，如图9所示。

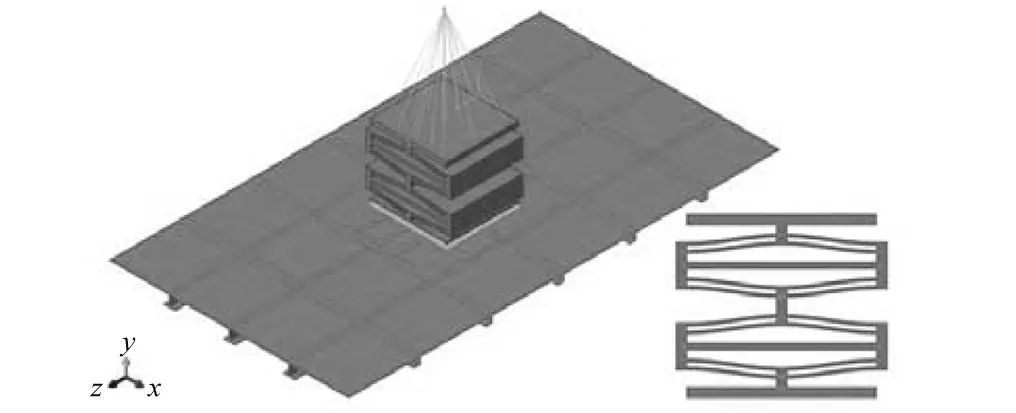
图9 具有四层双余弦梁的整体式抗冲击系统有限元模型Fig.9 Integral model with 4 layers of centrally-clamped cosine beams

为研究结构安装形式对抗冲击性能的影响，将抗冲器结构按纵向长度一分为二，安装于船体板架，建立如图10所示的分析模型。在下文中整体模型和分离模型分别用C和S表示。

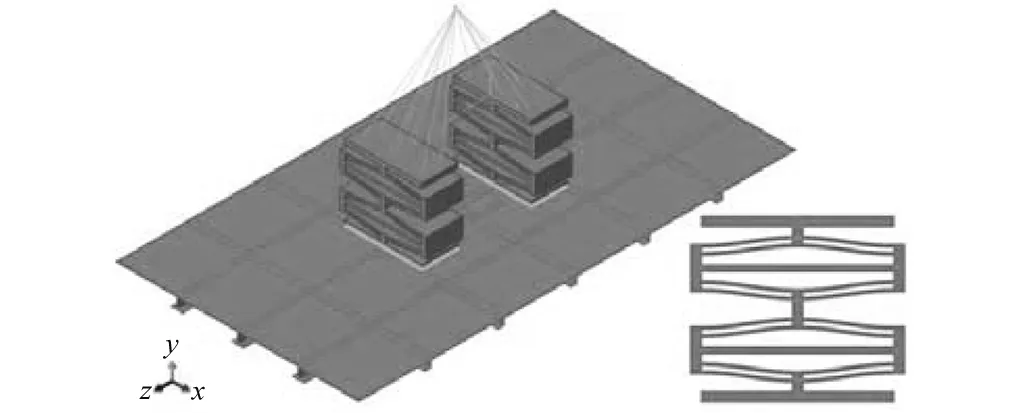
图10 具有四层双余弦梁的分离式抗冲击系统有限元模型Fig.10 Separate model with 4 layers of centrally-clamped cosine beams

为研究具有不同层数双余弦梁的系统抗冲击性能，取层数从1到4变化，分别建立整体模型和分离模型，如图11。限于篇幅，仅给出其横剖面图，模型其余部分参考图9与图10。

图11 具有不同层数双余弦梁的抗冲击系统横截面图Fig.11 Different layers ofcentrally-clamped cosine beams in shock isolator

冲击载荷根据德国军标BV043/85[11]所提供的资料，冲击谱采用三折线谱，由等位移段d0=0.02 m，等速度段v0=1.2 m/s，等加速度段a0=125 g(g=9.8 m/s2)组成。将冲击谱转换为由两段半正弦波构成的时间历程曲线

(6)

利用ABAQUS软件显式动力分析模块，研究系统的抗冲击性能。分析得到的加速度、速度、位移时间历程曲线如下图13～图15所示。模型名称以C4和S4为例，C表示整体模型，S表示分离模型，4表示具有4层双曲梁结构。曲线名称中，UP表示冲击经隔离后设备处的响应值，DOWN代表船底板架典型评价点平均响应值。

图13 具有不同层数双余弦梁的抗冲击系统加速度响应Fig.13 Acceleration response historyplots of a variety of shock isolation systems

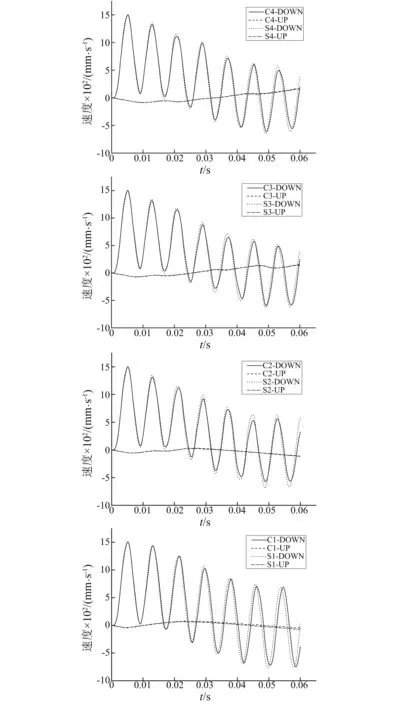
图14 具有不同层数双余弦梁的抗冲击系统速度响应Fig.14 Velocity response history plots of a variety of shock isolation systems

为了评价多层负刚度结构的冲击隔离效果，定义3个系数[12]，分别为加速度冲击隔离系数γa，速度冲击隔离系数γv和位移冲击隔离系数γu，如下式

(7)

式中：aup,max、vup,max、uup,max分别是隔离后设备加速度、速度和位移响应最大值，adown,max、vdown,max、udown,max分别是船底板架评价点的平均加速度、速度和位移响应最大值。计算得到的冲击隔离系数，如表3所示。

从图15和表3可以看出，本文提出的多层负刚度系统的冲击隔离系数非常小，抗冲击效果显著。

根据表3，对于整体式抗冲器，具有2层和4层负刚度双余弦梁时的加速度冲击隔离系数最小，而对于分离式抗冲器，具有1层和2层负刚度双余弦梁时的加速度冲击隔离系数γa最小；两种形式的抗冲器速度冲击隔离系数γv均是具有1层负刚度双余弦梁时最小，位移冲击隔离系数γu均是具有4层负刚度双余弦梁时最小。由于抗冲击要考虑到设备是否会撞击其他结构或相邻设备，位移受到最大行程制约，此外最大加速度响应是否超过设备允许的加速度值是抗冲器是否合格的判据，因此位移和加速度指标更为重要[13]。综合考虑可认为层数为4时的抗冲击性能最优。

图15 具有不同层数双余弦梁的抗冲击系统位移响应Fig.15 Displacement response history plots of a variety of shock isolation systems

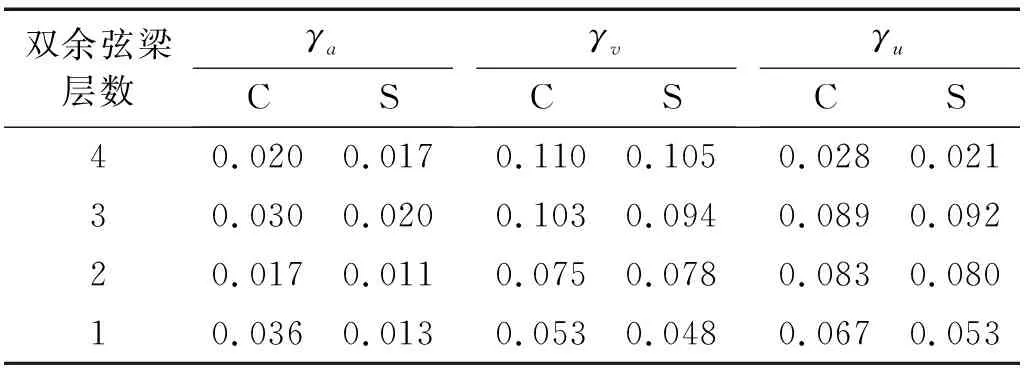
表3 不同层数双余弦梁模型的冲击隔离系数Tab.3 Shock isolation coefficientsof avariety of shock isolation systems

层数相同时，两种模型响应曲线很接近，但相比于整体模型，分离模型的加速度、速度、位移隔离系数均有一定程度的减小，因此抗冲击性能更佳。此外考虑到这种分离的模型便于在中部安装单向阻尼器，在冲击载荷的后端可以很快将能量耗散掉，因此有更高的实用价值。

以模型C4为例，给出冲击过程中能量的变化曲线如图16所示，可以看出动能明显转化为模型的应变能，储存起来，在冲击结束之后，将通过材料及其他形式的阻尼耗散掉。由于双曲梁位形的可恢复性，结构可以多次循环利用，因此，相比于主要依靠塑性变形的其它形式蜂窝抗冲击结构具有明显的优势。

图16 多层负刚度冲击隔离系统能量变化曲线Fig.16 Energy variations in a multilayer negative stiffness shock isolation system

4 结 论

本文提出将多层双余弦梁在垂向串联并安装到船体板架，形成抗冲击隔离装置，用于船舶设备的冲击防护。并对其在冲击载荷下的性能进行了数值分析。通过分析得到如下结论：

(1) 多层负刚度冲击隔离系统具有质量轻、(静)刚度大的特点。通过不同的尺寸参数、层数、列数的设计，可以调整其负刚度特性，并有解析公式为设计提供依据，设计过程简单方便。

(2) 多层负刚度冲击隔离系统的刚度呈现明显的非线性特性，因此线性谐响应分析已经不能满足要求，应采用考虑非线性的瞬态分析。计算结果表明，多层负刚度冲击隔离系统抗冲击性能优良，加速度、速度、位移在经过系统传递后均有非常明显的减弱。所设计的隔冲器理论上最大承受静载约371 kg，即在静平衡条件下能够支持设备，而在冲击载荷下因其负刚度特性产生屈曲，起到了保护设备的作用。

(3) 随着层数的减少，速度的冲击隔离系数有所减小，而位移和加速度的冲击隔离系数有所增加，抗冲击性能减弱。层数相同时，分离模型的加速度、速度、位移隔离系数相比于整体模型较小，因此抗冲击性能更佳。同时考虑到阻尼器等其它部件的安装，分离模型具有更好的实用价值。

多层负刚度冲击隔离系统采用3D打印成型技术，加工方便，加工缺陷小，力学性能优良，本文的研究成果可用于指导其设计与评估，在舰船安全性领域有很好的工程实用意义。