基于HHT的明清官式古建筑的模态参数识别方法
2018-11-01胡浩然
胡浩然, 杨 娜
(1. 北京交通大学 土木建筑工程学院,北京 100044; 2. 合肥市城市生命线工程安全运行监测中心,合肥 230000)
目前,针对明清官式古建筑的现场动力测试和模态参数识别的研究并不是很多,明清官式古建筑具有肥梁胖柱的构造特点,且存在年代久远,木构件本身的残损状况不一,整体结构的保护和修缮的力度也不尽相同,结构自身的各种参数性质分布也十分的离散,而且木结构本身也存在材性离散较大的问题,木构件之间的连接,木构件与屋面结构,木结构与墙体结构之间的连接状况也相当复杂,在进行现场动力测试时采集到的结构振动信号往往不满足平稳、线性的要求,而且信噪比较低,振动信号幅值小,因此,如何从现场测试中得到的振动信号中提取出结构的模态参数是一个比较困难的问题。针对低信噪比信号模态识别问题,本文提出了一种结合SSA的HHT方法,该方法能在低信噪比下识别出更多的模态参数,并提高信号的拟合优度[1]。
HHT方法被认为是近年来对以傅里叶变换为基础的线性和平稳谱分析的一个重大突破[2]。它不受傅里叶分析的局限,能描绘出信号的时频图、时频谱和幅值谱,是一种更具有适应性的时频域局域化分析方法[3]。但是在结构信号质量较差,信噪比较低的情况下,HHT方法中的EMD(Empirical Mode Decomposition)分解容易造成分解后的分量模态混叠的状况,需要进一步处理才能获得单一频率的本征模态分量[4-5]。
SSA方法是一种比较新颖的不基于数学模型的非参数分析方法,SSA的主要目的是用来将时间序列中不同频率的信号分离出来,并通过奇异值来表示不同信号中所含有的能力的相对大小。一般被用来进行寻找趋势项,提取周期信号,平滑和去噪[6]。
在本文中,基于现场实测得到结构振动的信号,首先对振动信号进行EMD分解[7],分解出结构的本征模态函数(Intrinsic Mode Function,IMF),但是由于古建筑自振频率低,且信号质量差,仅仅是EMD分解,并不能很好的将模态响应完全的分离开,而且分解出来的单个本征模态函数中经常会混杂着大量的噪声,会干扰后面的模态参数提取,因此,在得到IMF后,通过SSA方法对IMF进行进一步的处理,分离IMF中混杂的其他模态分量并降噪,然后将进过SSA处理后的IMF分量进行随机减量(Random Decrement Method,RDT)处理,得到结构振动的自由衰减曲线,对自由衰减信号进行Hilbert变换,得到信号的相位幅值谱,通过最小二乘拟合,得到结构的模态参数[8]。
1 改进的HHT方法进行模态参数识别
本文在普通的HHT方法的基础上结合SSA方法对结构模态参数进行识别,普通的HHT方法和改进的HHT方法流程如下图,途中,深黑色箭头给出的是普通的HHT识别方法,浅黑色箭头给出的是改进的HHT方法。
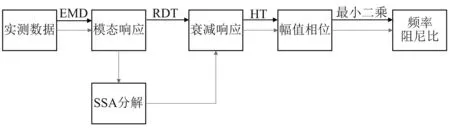
图1 改进的HHT方法和普通的HHT方法Fig.1 Improved HHT method and normal HHT
下文对本方法中涉及到的模态参数识别方法进行一个简要的介绍。
1.1 EMD分解
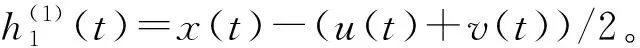
当一条信号h(t)满足以下两个条件时,可以看做是一个固有模态函数IMF:①|EP-ZP|≤1。 ②u(t)+v(t)=0。 EP为信号h(t)在时域内的极值点(包括极大值与极小值)的个数,ZP为信号h(t)时域内零点的个数;u(t)为h(t)在时域内由极大值确定的上包络线,v(t)为h(t)在时域内由极小值确定的下包络线[10]。
1.2 SSA方法
SSA分解是一个新型强大而且实用范围非常广泛的数据信号处理方法,通过SSA分解,可以将信号分解为多个独立而且有实际意义的信号分量(如趋势项,周期信号,噪声等等)之和[11]。分解完成后的每一阶信号分量对应该分量的奇异值。
将待处理信号x(t)=(x1x2x3…xn), 嵌入一个Hankel矩阵
(1)
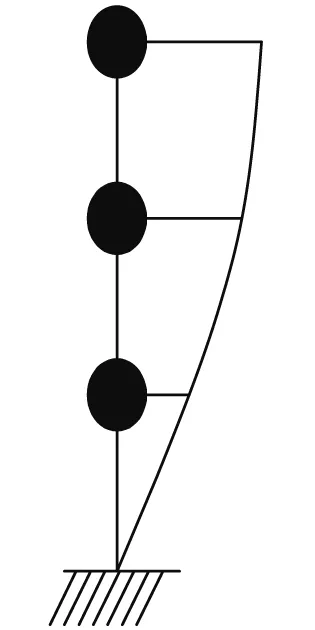
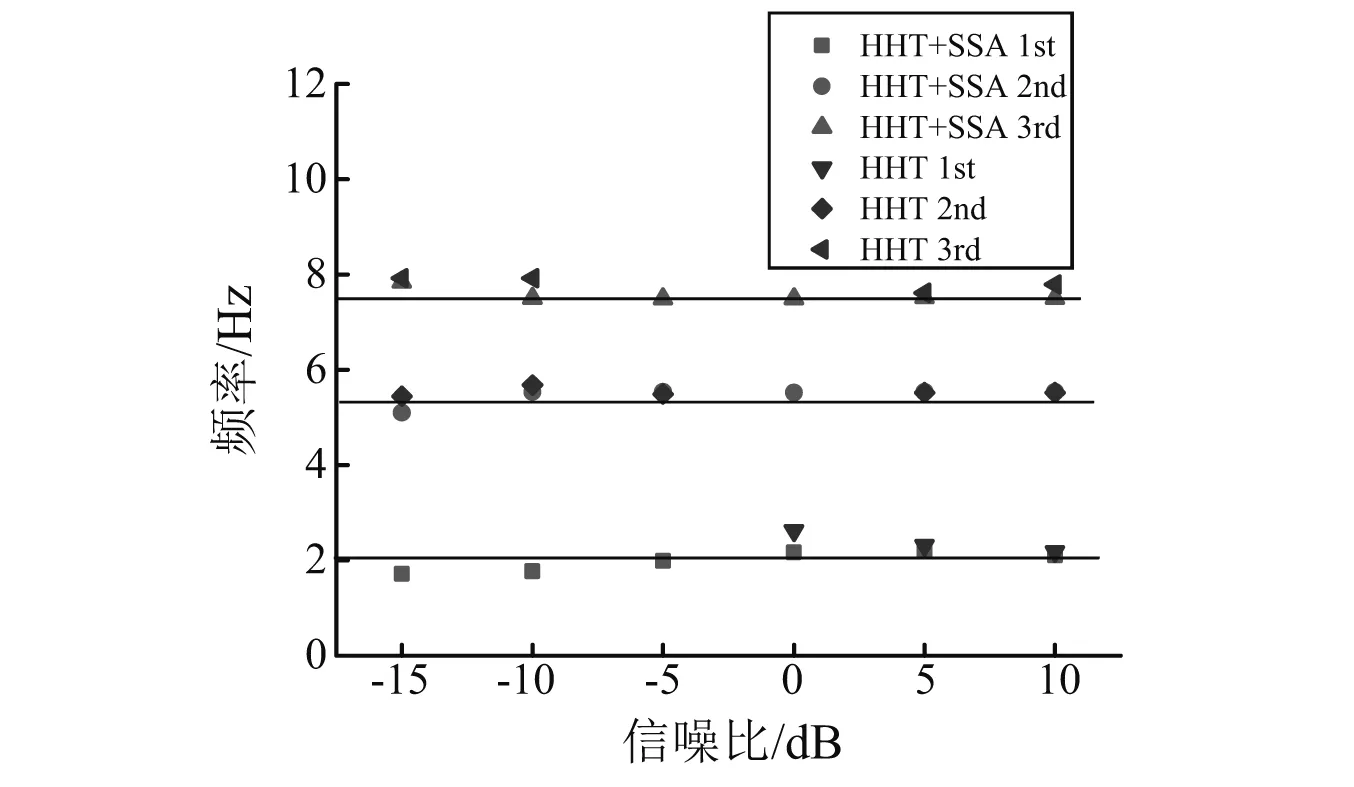
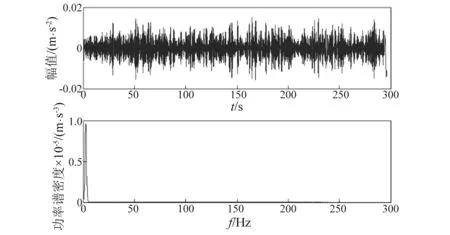
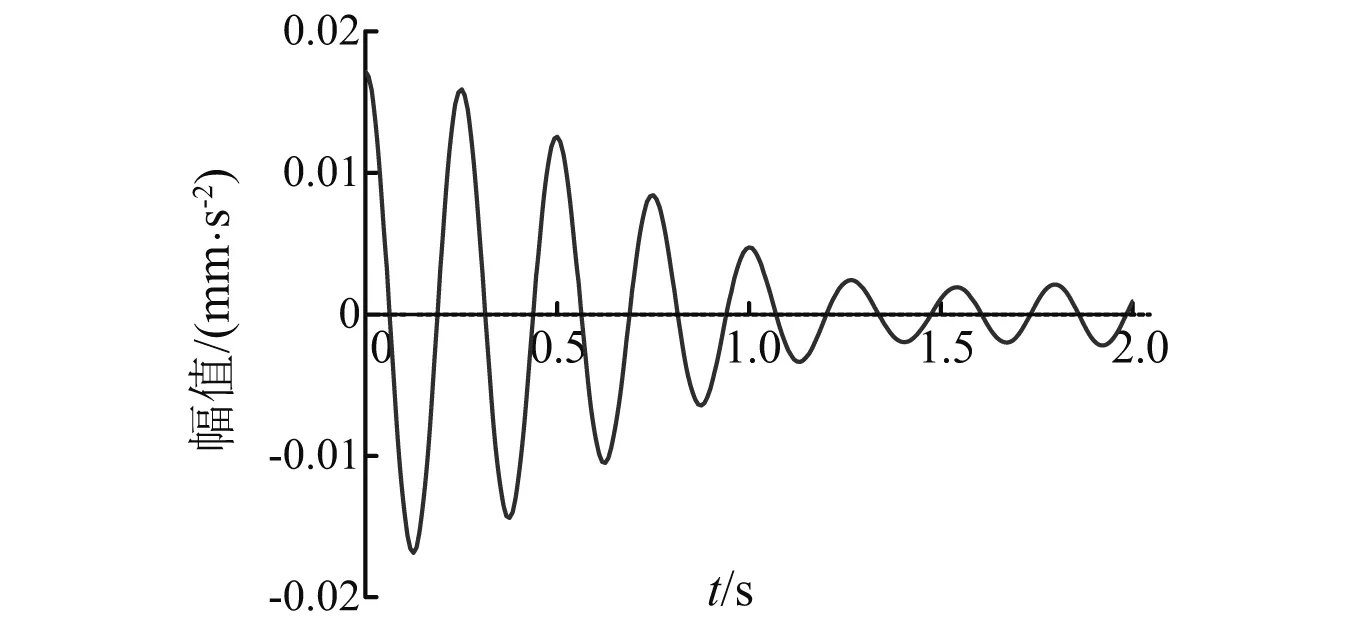
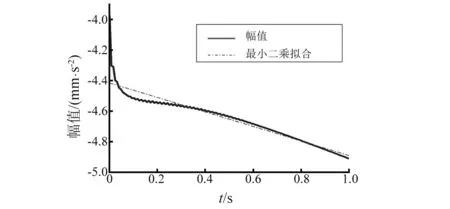
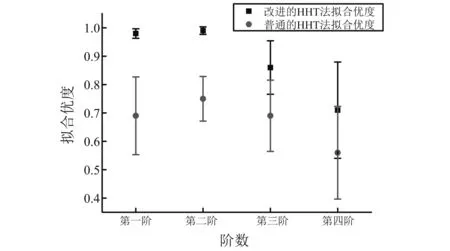
Hankel矩阵的行数L满足1 U=(U1U2…UL),V=(V1V2…VL) (2) S=(diag(σ1σ2…σL),0) (3) 则X可以分解为L个矩阵的和 (4) 对于分解之后的矩阵,我们可以选择需要的子矩阵留下,不需要的剔除。一般而言,一个谐波分量对应着一对耦合的奇异值和特征向量,趋势项对应着单独的一个奇异值和一个特征向量,噪音对应的奇异值一般远远小于其他分量对应的奇异值,奇异值的大小和分量的能量有关[12]。矩阵重组之后,得到新的矩阵有效矩阵,对其进行对角平均,即可得到经过SSA分解处理后的信号向量。该方法是为了消除信号中的混叠模态,因此,在重组时,应该将奇异值比较接近的几阶信号重组。 改进的HHT方法在针对低信噪比的信号时,有更好的识别结果,为了对该方法进行评估,建立一个三个自由度的数值模拟模型,如图2~5所示。 图2 三自由度模型Fig.2 3DOF modal 图3 第一阶振型Fig.3 1st mode 图4 第二阶振型Fig.4 2nd mode 图5 第三阶振型Fig.5 3rd mode m1=m2=2m3=1 kg;k1=k2=k3=610 N/m。 在m1,m2,m3上加入白噪声激励。通过Newmark法、中心差分法和Wilson法求解结构的位移、速度、加速度响应。取NewMark法计算的m3处的振动响应进行后续分析。数值算例中,阻尼的识别结果较差,以频率识别结果来说明该方法的可用性。 图6 原始信号Fig.6 Original signal 通过改进的HHT方法和普通的HHT方法对数据进行分析,结果如表1、2和图7所示。 表1 改进的HHT方法计算的频率结果Tab.1 Frequency results by Improved HHT 表2 普通的HHT方法计算的频率结果Tab.2 Frequency result by normal HHT 图7 不同信噪比下两种方法计算的频率结果对比Fig.7 Comparison of frequency results calculated by two methods under different SNR levels 从数值模拟的分析的结果可以看出,信噪比越高,改进的HHT方法和HHT方法识别出的自振频率精度越高;但改进的HHT方法在低信噪比时,能够更好的识别出更多的模态参数,在本文的数值模拟中,普通的HHT方法在信噪比大于等于5 dB时才能识别出所有的模态参数。 咸福宫西配殿是一座典型的明清官式古建构造。西配殿的现场照片如图8、9所示,柱网分布如图10所示。 图8 西配殿位置示意图Fig.8 West peidian’s position 图9 西配殿现场照片Fig.9 Field picture 图10 西配殿柱网编号Fig.10 Column number 咸福宫西配殿共有8根柱子,动力测试的测点主要是测量柱架层的动力特性,故测点布置在八根柱头附近。由于现场条件限制,测试分两次进行。 西配殿现场动力测试时长在半个小时左右,采样频率为128 Hz,采用环境激励法。以一条信号为例,测点分解出来的IMF分量中,前六阶的幅值远大于后面的分量的幅值,存在数量级上的差异,因此认为前六阶IMF分量对应着结构的模态分量。对第六阶阶分量进行SSA分解,取前两阶重组,如图11、12所示。 图11 第六阶IMF分量图Fig.11 6th of IMF component 图12 信号SSA分解后奇异值分布Fig.12 Distribution of singular value 对SSA分解后的信号进行随机减量处理,得到的自由衰减曲线,如图13~15所示。 图13 第六阶IMF自由响应曲线Fig.13 The free decay curve of 6th IMF 图14 第五阶IMF自由响应曲线Fig.14 The free decay curve of 5th IMF 图15 第四阶IMF自由响应曲线Fig.15 The free decay curve of 4th IMF 以第六阶自由衰减响应曲线为例,进行Hilbert变换,得到对应的幅值谱和相位谱,如图16、17所示。 图16 幅值谱Fig.16 Amplitude spectrum 图17 相位谱Fig.17 Phase spectrum 结构的前四阶自振频率分别为:1.61 Hz,2.10 Hz,2.71 Hz,4.18 Hz。对应的阻尼比为3.19%,3.56%,4.64%,3.51%。 通过数据驱动的随机子空间法(SSI)对数据进行分析的结果和改进的HHT方法计算的结果的对比分析,如表3所示。 表3 SSI和改进的HHT方法结果对比Tab.3 Comparison of SSI and HHT method SSI计算的结果比改进的HHT方法偏大一些,阻尼比的差异比较大。 本文使用的改进的HHT方法相比于普通的HHT方法,多了一步用SSA分解对数据进行处理的过程。 木结构的自振频率底,相邻两阶频率接近,因此EMD分解出来的IMF会出现频段重叠的现象,直接进行RDT的话得到的自由衰减曲线会带有拍振的性质,后续进行Hilbert分解以及最小二乘拟合时,拟合的离散型较大,不能分辨出有效的模态参数。SSA的主要作用是将数据中有效频段的信息过滤出来,去除无用的干扰信息。 本文以进行最小二乘拟合时的拟合优度为指标,对比改进的HHT方法和普通的HHT方法的差异。 由表4和图18可见,经过SSA过滤后的信号,拟合优度有显著提高。说明改进的HHT方法相比于普通的HHT方法,结果的离散性大大降低,从计算结果中提取模态参数的准确性提高。 表4 拟合优度对比Tab.4 Goodness of fit 图18 拟合优度Fig.18 Goodness of fit 本文提出了一种基于HHT的改进的模态参数识别方法,并通过数值模拟和实际工程应用说明了该方法的可用性。 (1) 本文中采用的改进的HHT方法在数值模拟和实践中都得到了较好的应用,并且在采集到的振动信号信噪比较低的情况下,相比于普通的HHT方法有更好的识别效果,可以识别出更多的有效的振动参数信息。 (2) 改进的HHT方法可以处理非平稳、非线性信号,且在进行线性拟合时拟合优度有所提高。 (3) 对于木结构古建筑而言,由于结构自身的特性,自振频率较低,而且分布密集,存在年代久远,木构件本身的残损状况不一,整体结构的保护和修缮的力度也不尽相同,结构自身的各种参数性质分布也十分的离散,而且木结构本身也存在材性离散较大的问题,木构件之间的连接,木构件与屋面结构,木结构与墙体结构之间的连接状况也相当复杂,在处理大型木结构在环境激励下的振动信号时改进的HHT方法往往能够取得较好的结果。
σ1>σ2>…>σL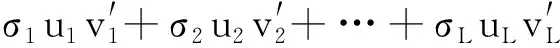
2 改进的HHT方法评估







3 改进的HHT方法进行古建筑模态识别









4 结 论
