重型车辆转向节臂强化路耐久性断裂试验*

门玉琢， 于海涛， 于海波

(1. 吉林工程技术师范学院汽车工程学院 长春，130012) (2. 哈尔滨师范大学教学实验设备管理中心 哈尔滨，150025)

引 言

汽车的耐久性主要是由其各结构及零部件的疲劳寿命决定的，大多数情况下零部件所承受的是随时间发生变化的动态载荷，它们一般是随时间变化的随机函数[1]。在这种载荷作用下零部件会发生疲劳失效或破坏，即零件在经受一定时间的循环载荷作用以后发生疲劳失效。试验场可靠性试验着眼于模拟汽车在实际使用环境中所碰到的最恶劣工况，即造成汽车零部件疲劳损伤主要部分的工况。为缩短可靠性试验时间，试验条件变得越来越苛刻，这主要是通过建造更恶劣的试验道路和加快车速来实现[2-3]。转向节臂作为重型汽车转向系统的重要部件，起到传递转向力作用，其可靠性对行车安全至关重要，在整个寿命里程内不允许其发生断裂[4-6]。从现有的转向系统可靠性研究成果看，各大汽车公司主要偏向于动力传动系和承载结构的研究，而转向系构件的故障分析、数据测试相对复杂，相关研究资料较少，尤其在试验场强化路可靠性试验阶段。

根据某重型载货汽车转向系可靠性试验结果，笔者测量转向节臂锥体根部断裂位置附近的弯曲应变及转向系相关数据，并结合材料特性和工艺装配精度分析，确定转向节臂断裂机理。

1 结构的疲劳

疲劳是零部件由于循环载荷引起的局部损伤过程，循环加载期间，在最高应力区域会产生局部塑性变形，这种变形将引起零部件的永久损伤和裂纹扩展[6]。尽管大多数零部件名义上都具有循环弹性应力，然而对于有切口、焊缝或其他存在应力集中的零部件，会形成局部循环塑性变形，因此利用局部应力-应变法预测零部件疲劳寿命更具有效性。

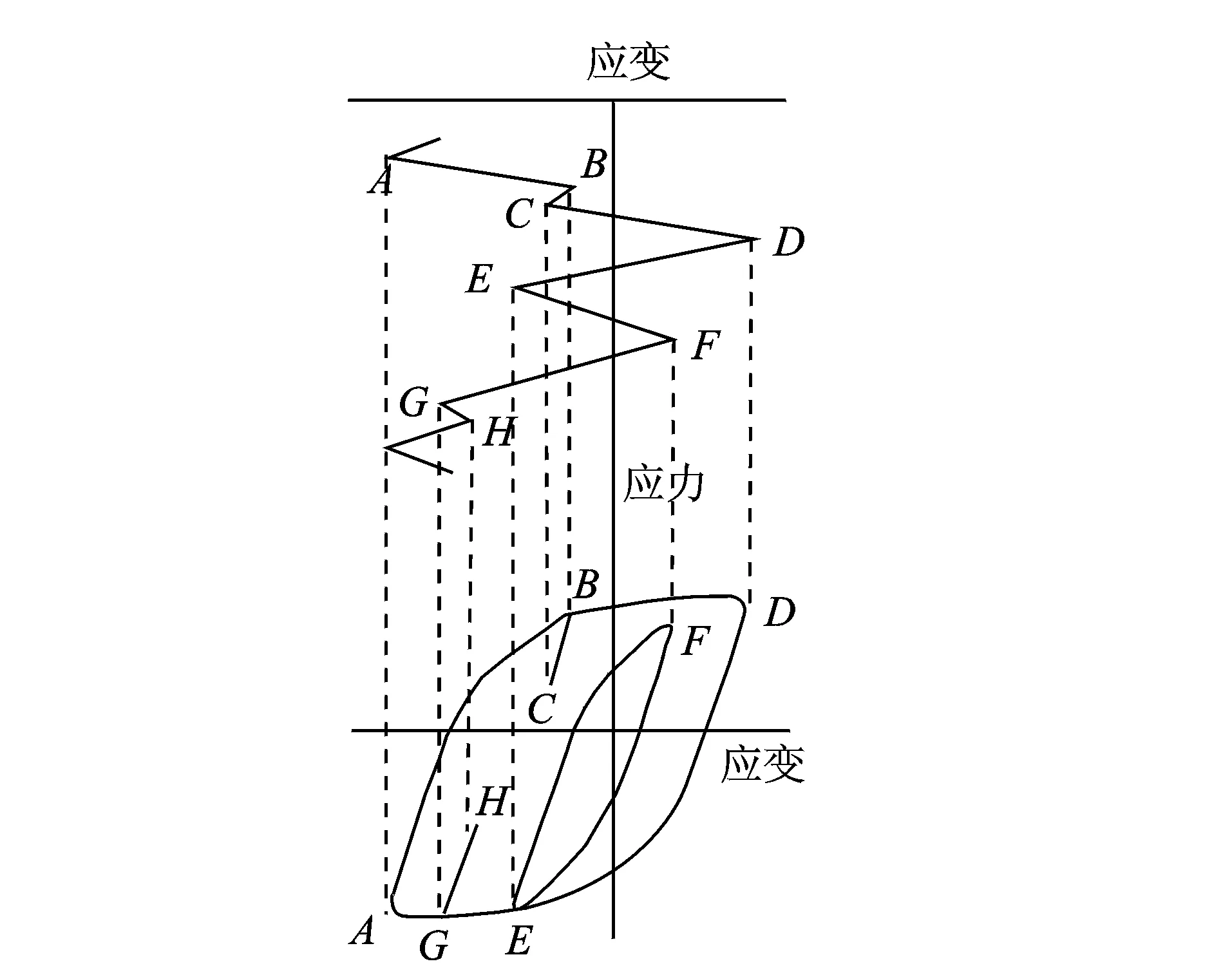
图1 雨流计数法原理Fig.1 Rain-flow counting principle

转向节臂发生的断裂主要是由于局部应力波动循环而引起的，应用雨流计数法可以把载荷时间历程处理成幅值-均值-循环次数的雨流循环计数矩阵[5-6]。结构和零部件的疲劳损伤就是由循环载荷产生的，将整个时域载荷循环引起的疲劳损伤通过累积得到总损伤[3,7]，雨流计数过程如图1。图中两条平行实线和垂向实线分别为坐标系的横轴与纵轴，上半部分的实曲线为实测的应变数据，下面的实曲线为其雨流计数后的滞回环曲线；字母A～H为峰谷值数据点，虚线为峰谷值计数后对应点连接线。

转向节臂锥体根部断裂位置难以粘贴应变片来测量局部应变，只能把应变片粘贴在断裂口附近[3]测试名义应力。然后将测试的名义应力谱转换成危险部位(断裂位置)的局部应力-应变响应[5,8]。

根据Neuber法则，循环加载时结构或部件的缺口根部易产生裂纹[9-10]，利用应变片测试的名义应力与局部应力-应变幅值间的关系为

(1)

其中：Kf为疲劳缺口系数;E为弹性模量;ΔS和Δε为应变片测试的名义应力与应变范围;Δσn和Δεn为缺口根部的局部应力与应变范围。

疲劳缺口系数[3,5]的计算式为

Kf=1+(Kt-1)/(1+a/r)

(2)

其中：a为材料的常数;r为疲劳缺口根部的圆角半径;Kt为理论应力集中系数。

断裂位置的局部应力-应变范围的滞回环曲线方程为

(3)

其中：n′为循环硬化指数;K′为循环强度系数。

联合式(1)和式(3)有

(4)

联立式(3)和式(4)，可求出转向节臂断裂处局部应力-应变响应各个滞回环的εn和σn。

设每个滞回环的平均应力σ与应变范围Δεi分别为

Δεi=|ε1i-ε2i|

(5)

σ0i=(σ1i+σ2i)/2

(6)

把上述平均应力σ0i和应变范围Δεi代入到Manson-Coffin公式进行平均应力修正[3],即

(7)

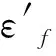
解方程式(7)求出疲劳寿命Nf i。设第i级应力幅值产生的疲劳损伤为Di，则

Di=ni/Nfi

(8)

其中:ni为载荷第i级幅值下循环次数。

利用Miner疲劳线性累积损伤法则，将各级疲劳损伤进行累积得到的总疲劳损伤D为

(9)

其中:M为载荷幅值等级。

当D等于1时转向节臂即发生疲劳断裂。

转向节臂的材料为40 Cr，疲劳损伤计算中与材料相关的参数取值见表1。

表1 转向节臂材料相关疲劳参数取值

2 载荷测试与疲劳损伤计算

2.1 载荷测试方案

载荷谱是汽车结构及零部件疲劳寿命、损伤计及疲劳耐久性试验的基础，试验中测试的载荷一般指位移、加速度、转矩及应变等。计算之前需确定载荷谱排列顺序、循环次数及幅值。本次试验具体的测试参数见表2,布置的与转向系统相关联的测试传感器，如图2～5所示。

表2 试验主要测量参数

图2 粘贴全桥应变片的转向节臂Fig.2 Full bridge strain gages on steering knuckle arm

图3 测量转向拉杆拉力的应变片Fig.3 Measurement strain gages for steering rod

图4 测量转向横拉杆位移传感器Fig.4 Measurement displacement sensor for steering rod

图5 前轮轴头的加速度传感器Fig.5 Acceleration sensor on front axle

2.2 疲劳损伤计算

利用Glyph Works疲劳分析软件计算局部应力-应变的疲劳损伤，需要对实际测试的载荷信号进行“浓缩”处理，剔除对疲劳损伤贡献度较小的信号。eDAQ数据采集仪通过传感器测试整个试验过程数据，由于记录的通道数较多、数据计算量庞大，文中只以车辆满载为例，计算强化路的转向节与转向节臂疲劳损伤，测试的时域应变曲线如图6。

图6 转向节与转向节臂的应变曲线Fig.6 Strain of steering knuckle and steering knuckle arm

图6中，(a～d)分别为右侧转向节应变、右侧转向节臂应变、左侧转向节应变、左侧转向节臂应变时域信号。利用这些数据计算疲劳损伤前，首先要对试验数据的重复性进行检查，保证数据的正确性，然后进行预处理，包括去“毛刺”、漂移矫正、滤波等，最后将预处理后的“干净”试验数据输入到GlyphWorks软件的应变寿命模块，并对其属性进行定义，包括Manson-Coffin平均应力的修正、疲劳缺口系数Kf及材料的属性等参数。

疲劳损伤的计算包括名义应力法和局部应变法。名义应力法的平均应力修正应用的是Goodman方程，本次试验采集的应变信号应用局部应变法计算损伤，因此需要用Manson-Coffin方法做平均应力修正，其修正曲线如图7所示。

图7 Manson-Coffin平均应力修正模型Fig.7 Manson-Coffin mean stress correction model

经Manson-Coffin平均应力的修正后的应变-寿命(ε-N)曲线是一个曲线族，共计64条(雨流直方图区间为64)，这样就实现了考虑每一应力均值后计算的疲劳损伤。雨流计数的直方图矩阵如图8所示，雨流计数结果见表3。

图8 三维直方图雨流矩阵Fig.8 Rainflow matrix of 3D histogram

图8为雨流计数结果直方图，即幅值-均值-循环次数的关系，从图中可以看出，小幅值及均值在0附近的循环次数较多，这与雨流计数的规则是一致的。表3为应变数据为雨流计数的幅值、均值及循环次数。

表3 应变信号的雨流计数结果

根据Miner疲劳损伤计算方法，将不同幅值、均值下的疲劳损伤进行累积，即可得到总的疲劳损伤，如表4。表4为应变数据的雨流计数幅值、均值与疲劳损伤。表3与表4的雨流计数及疲劳损伤计算数据量较大，这里只列出了部分计算结果。最终总疲劳损伤见图9、图10及表5。

试验测量了三种装载(空载、半载及满载)工况数据，根据“某试验场汽车产品定型可靠性行驶试验标准”，左右两侧转向节臂断裂里程接近，主要集中在4 200～4 400 km，且有很好的重复性，没有通过可靠性考核的标准。从转向节和转向节臂的强化路疲劳损伤分布曲线看，装载载荷大小对疲劳损伤影响较小。所有强化路中，卵石路对断裂部位造成的损伤所占比例最大，超过了90%。此时转向节与转向节臂由于强化路路面的凹凸不平而引起左右转向轮的运动“步调”不同步，以及结构装配和加工工艺精度的偏差，在转向节臂椎体根部产生了局部高集中应力，最终发生弯曲疲劳断裂。

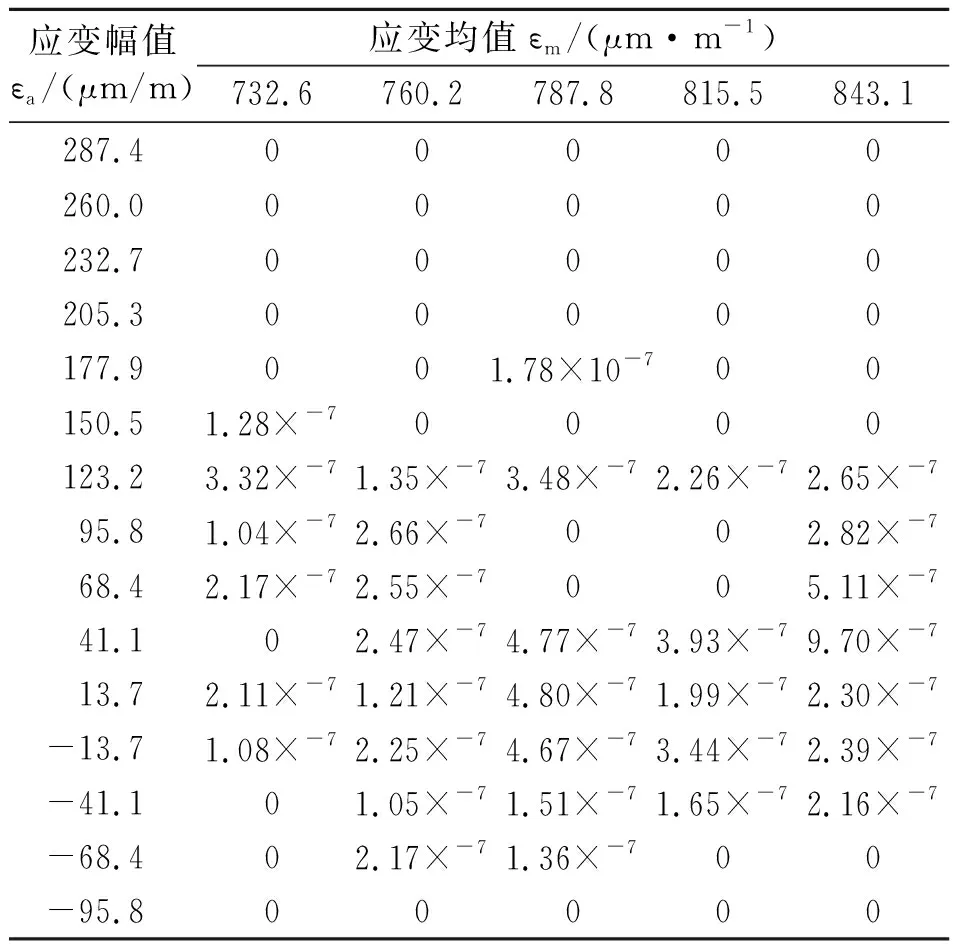
表4 疲劳损伤计算结果

图9 试验场强化路左侧转向节臂疲劳损伤Fig.9 Fatigue damage of left steering knuckle arm on enhancement roads

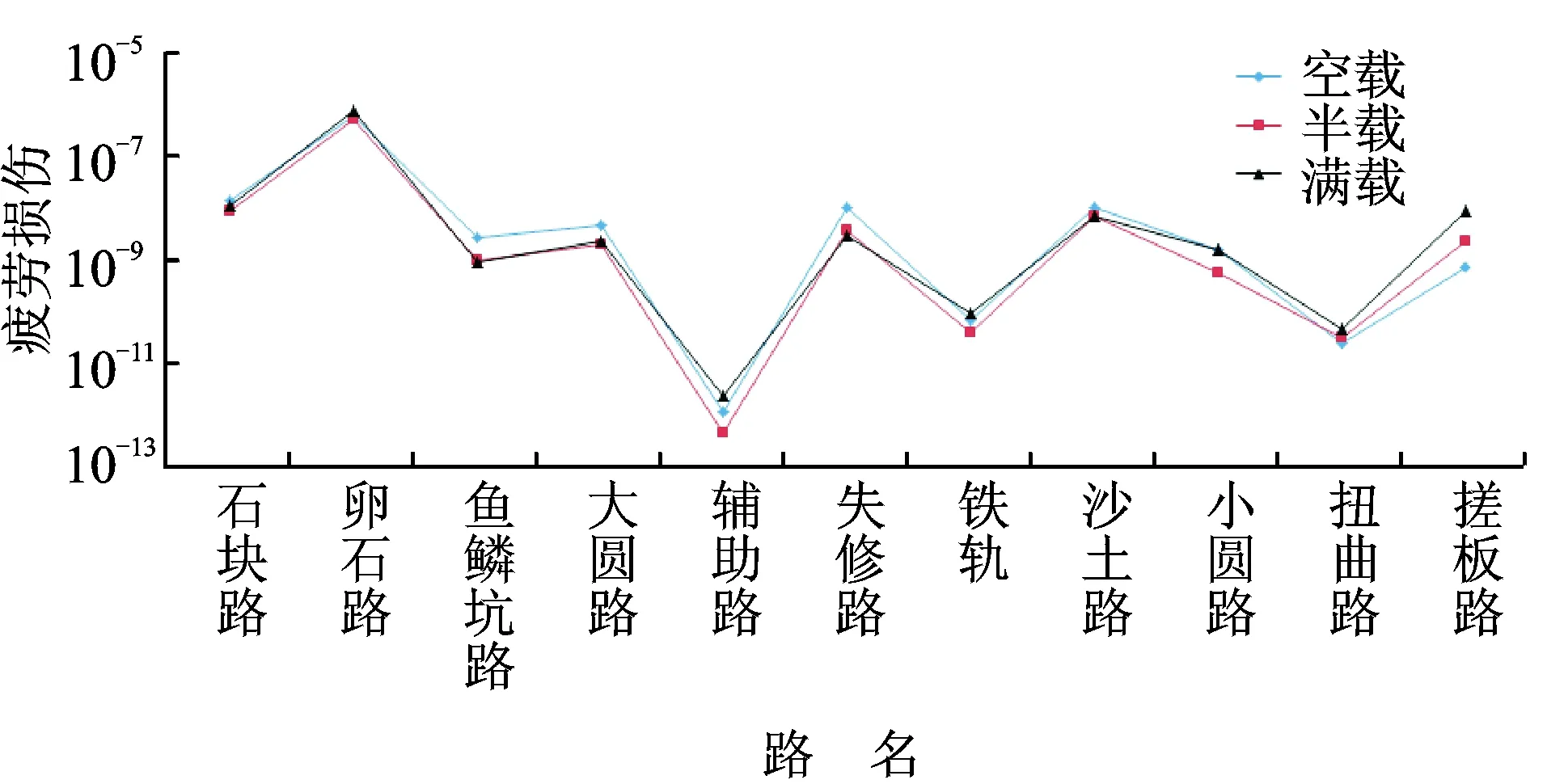
图10 试验场强化路右侧转向节臂疲劳损伤Fig.10 Fatigue damage of right steering knuckle arm on enhancement roads

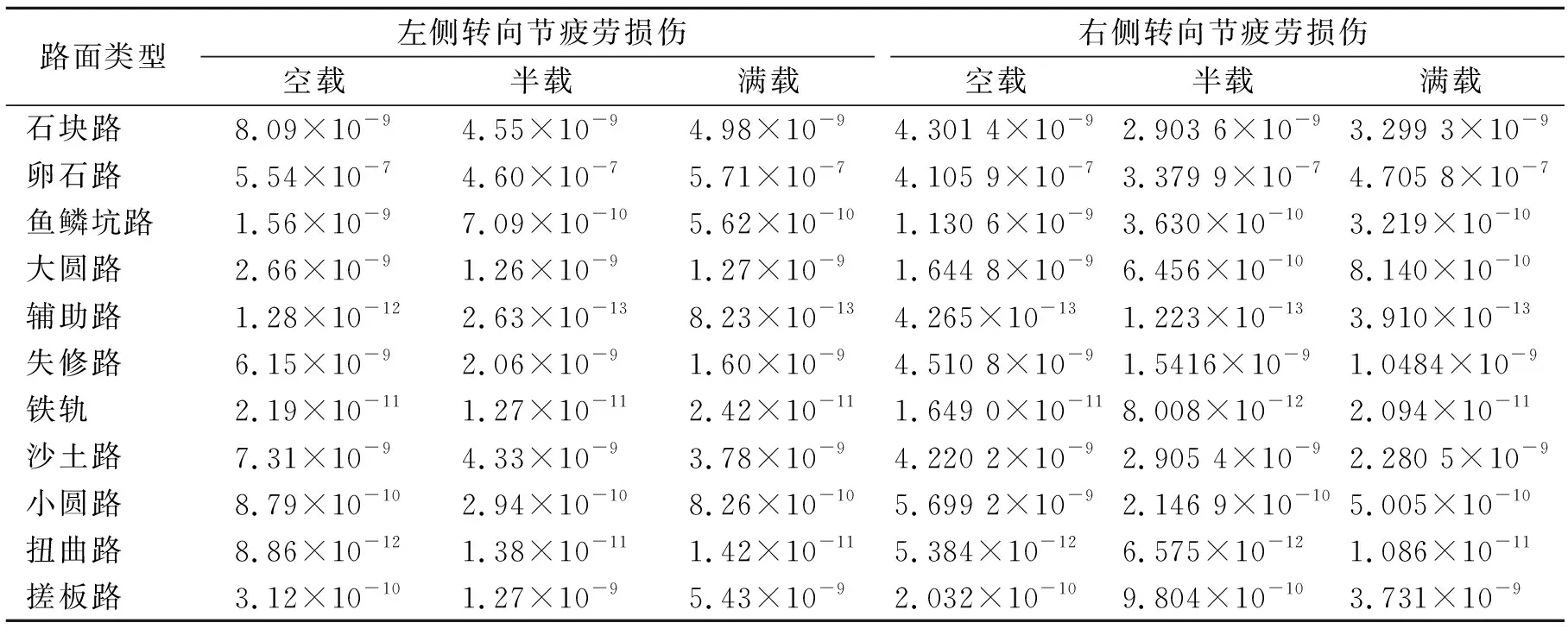
表5 试验场强化路转向节疲劳损伤

3 材料特性与工艺装配精度

3.1 材料特性

图11 转向节臂断口形貌Fig.11 Fracture surface feature of steering knuckle arm

试验中断裂的转向节臂如图11，断裂位置见图中矩形标识处，左右转向节臂断裂里程接近、位置相同，均发生在转向节臂锥体根部。断裂位置刀痕明显，断口与刀痕平行，有多个清晰可见的“台阶”。同时在裂纹源区域也存在多个明显的“台阶”，裂纹源形貌如图12所示，这些“台阶”处易产生高集中应力。

图12 转向节臂裂纹源形貌Fig.12 Crack source of steering knuckle arm

对断裂样品件材料进行维氏硬度检测，维氏硬度由于试验时加载的压力小，压入深度浅，对工件损伤小，特别适用于测量零件的表面，经常用于实验室及科研方面检测。维氏硬度检测位置分布在断口表面，3个测点呈120°角，检测结果见表6。从测试结果看，4个样件件分别在3个测试点的维氏硬度数据接近，同时满足设计技术条件要求。

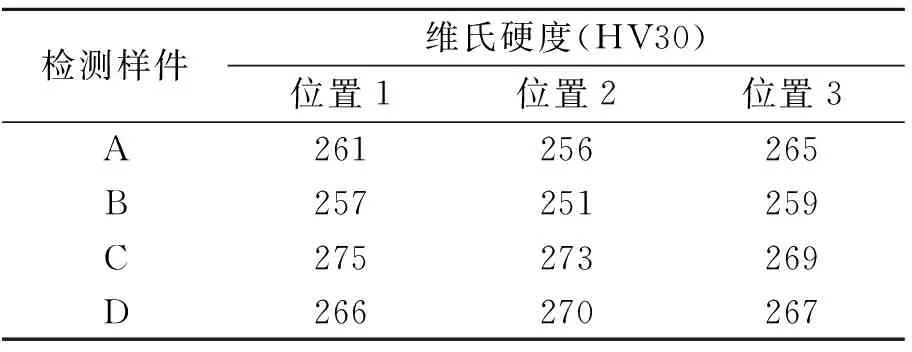
表6 维氏硬度检验结果

4个样品件的化学元素含量检测结果见表7。可以看出，A,C样件的碳元素略有偏高，其他化学元素的含量均符合设计条件。金相组织检测结果：A样件的回火索氏体为1级，B样件回火索氏体+贝氏体+少量铁素体为3级，C样件回火索氏体+贝氏体+少量铁素体也为3级，D样件回火索氏体为1级。

表7 化学元素含量百分比

3.2 工艺装配精度

被检验样品转向节臂的锥面粗糙度为1.251 9，圆度为0.006 9，锥度为5°44′0″。与转向节臂装配的转向节端面粗糙度为1.457 6，内孔粗糙度为1.523 1，圆度为0.010 9，锥度为5°43′39"。转向节臂与转向节的锥度检验结果偏差较大，未满足图纸设计要求。转向节臂、转向节锥孔面表面粗糙度检测结果远超出设计精度要求。

3.3 断裂裂纹分析

通过对转向节臂的材料特性和工艺装配精度分析，发现该批次样品断裂性质一致，均因受到过大冲击载荷而发生弯曲疲劳断裂，由于裂纹源表现出对刀痕的极大敏感性，因此应注意工艺。转向节臂与转向节装配接触面积只有30%，也不符合设计标准。

4 结束语

转向节臂材料的硬度、化学元素含量以及金相组织检测结果均满足设计技术条件，断裂裂纹表现出了对刀痕的极大敏感性，应提高加工工艺精度以增加其强度。转向节臂与转向节锥孔面表面粗糙度没有达到设计精度要求，转向节臂与转向节装配接触面积只达到30%，使锥面由均匀受力变为局部受力；车辆装载载荷大小对转向节臂的疲劳损伤无明显差异，损伤的最大值主要集中在强化路中的卵石路，路面的凹凸不平而引起左右转向轮出现运动学干涉，在转向节臂椎体根部产生了较大局部高集中应力而发生弯曲疲劳断裂。