基于LMD-MS的滚动轴承微弱故障提取方法*

王志坚， 吴文轩， 马维金， 张纪平， 王俊元， 李伟伟

(中北大学机械工程学院 太原，030051)

引 言

在旋转机械中，轴承是至关重要的一部分，而轴承的磨损也是不可避免的[1-5]，轴承磨损的初期信号较为微弱，很难在强噪声的背景下被发现，不采取相应的措施就会导致轴承故障，严重时甚至会导致重大的事故，造成经济损失和人员伤亡，因此对轴承早期故障信号的提取一直深受重视[6-9]。滚动轴承故障主要可以归纳为内圈、外圈的磨损以及滚动体的点蚀，当故障发生时会产生周期性的脉冲信号。由于噪声的干扰，早期故障信号提取一直是故障诊断的重难点，现有的故障诊断方法除传统的傅里叶变换，还有小波分解及经验模态分解等方法。

在经验模态分解(empirical mode decomposition，简称EMD)方法的基础上，Smith等[10-12]提出了一种时频分析法：局部均值分解其本质是将实测信号按频率的高低分成不同的功能分量，而每一个PF分量都是由一个包络信号与一个纯调频信号相乘而来，将分解后的PF分量进行频域分析就可以得到完整的时频分布。

但是LMD的缺点也比较明显，与EMD方法相比，LMD的模态混叠现象虽然有所减轻，但模态混叠现象依然严重，导致时频分布混叠，产生杂乱的PF分量，进而无法从中提取所需的时频信息[13-14]。

为了解决EMD的模态混叠现象，许多专家相继提出了不同方法，在这些方法中掩膜法因其计算效率高、后期处理能力强的优点而备受关注，但是到目前为止，掩膜法还没有应用在LMD的模态混叠问题上[15-17]。

基于以上原因，笔者将掩膜法引入到LMD方法中，发现掩膜法具有一定的消噪功能，通过掩膜信号法削弱噪声对PF分量的影响，并加入了文献[18]中的频率能量均值参数作为依据，细化故障频率所处频带，在对仿真信号和滚动轴承微弱的故障信号分析中，成功削弱了LMD的模态混叠现象，提取了故障特征。并通过计算信号处理前后的信噪比与峭度比验证方法的可行性。

1 LMD方法

针对原始信号x(t)，LMD分解步骤如下。

1) 根据所有的局部极值点ni，求出所有局部极值平均值mi和包络估计值ai：用滑动平均法处理后得到局部均值函数m11(t)和包络函数a11(t)。

3) 得到包络信号

(1)

4) 得到第1个PF分量

PF1(t)=a1(t)s1n(t)

(2)

5) 将PF1(t)从x(t)中分离，获得u1(t)后，将其作为新的原始信号重复以上计算过程得到u2(t)，直到uq(t)为单调函数停止迭代

u1(t)=x(t)-PF1(t)

(3)

6) 原始信号被分解为

(4)

2 MS方法

掩膜法(mask signal method，简称MS)的基本原理为采用加减后取平均方法减小平滑处理积累的误差值，削弱模态混叠与噪声，突出平均瞬时频率附近的峰值，其中寻找合适的掩膜信号s(t)是掩膜法的关键。

假设t为时间，x(t)为原始信号，τ为积分变量，对原始信号x(t)进行希尔伯特变换，得到y(t)，改造后得z(t)，即

(5)

z(t)=x(t)+jy(t)=ai(t)ejφi(t)

(6)

根据幅值函数ai(t)与相位函数φi(t)瞬时相位，求得瞬时频率为

(7)

根据能量均值法[18]可以计算出

(8)

掩膜法在对不同信号处理时选取的平均幅值与平均瞬时频率也不同。面对x(t)时，a(t)是x(t)的包络幅值，f1(t)是x(t)的瞬时频率，所以确定的掩膜信号为

(9)

根据经验法则，a0通常取信号分量平均幅值的1.6倍最合适[19]。

创建一个掩膜信号s(t)，分别使得

x+(t)=x(t)-s(t)

(10)

x-(t)=x(t)-s(t)

(11)

将x+(t)和x-(t)结合后就可以得到原始信号为

(12)

以式(13)的仿真信号为例，验证掩膜法的性能。仿真信号如图1所示，图1(a)，(b)，(c)的频率分别40，80，130 Hz。

x(t)=sin(80πt)+0.8sin(160πt)+

cos(260πt)+1.5nnoise(t)

(13)

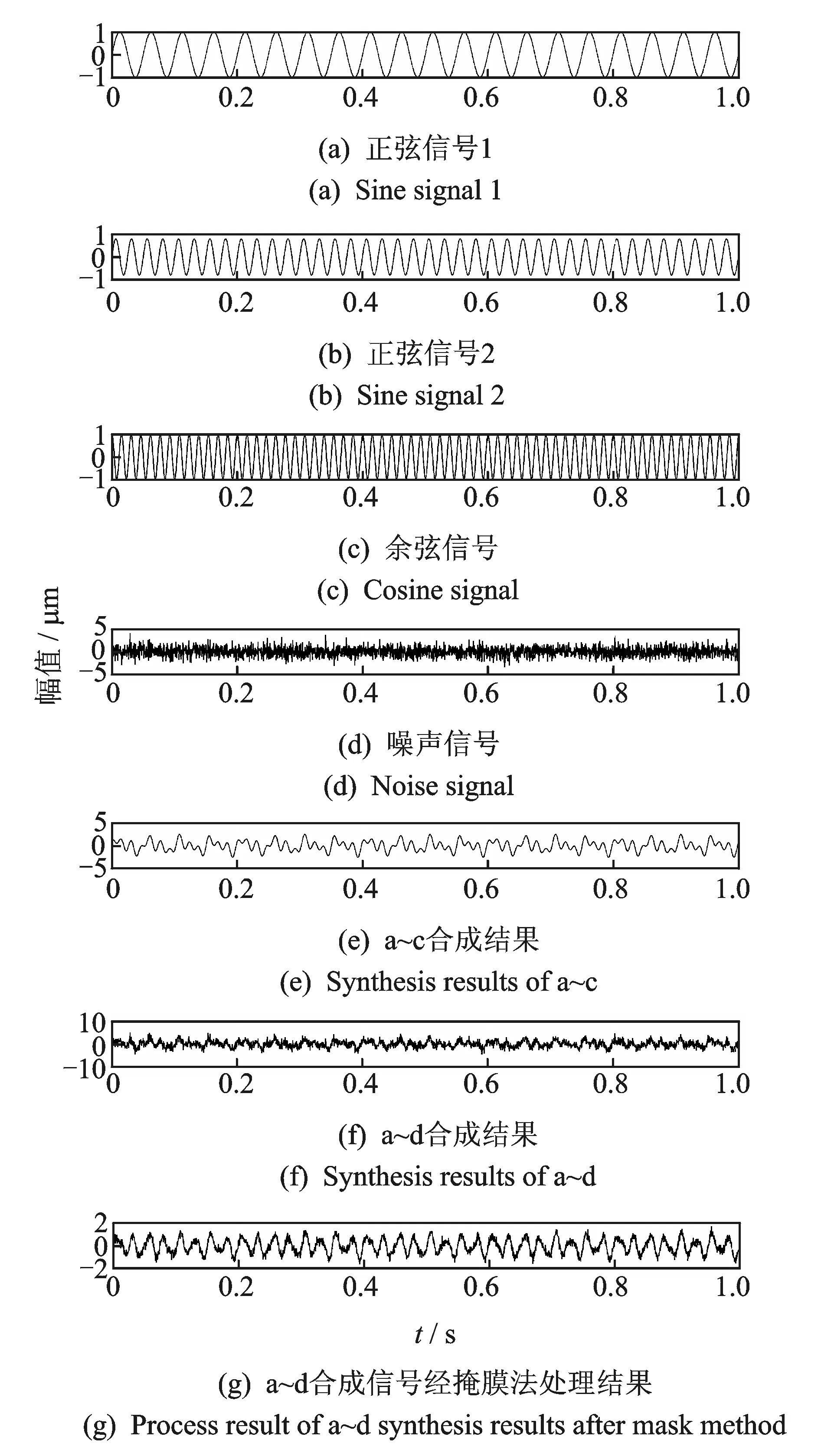
图1 仿真信号Fig.1 Simulation signal

从图1中的(e)，(f)，(g)图结果可以看出，掩膜法具有一定的降噪能力，并且(g)图中的波形也发生了改变；从图2中(f)，(g)的时频域图对比结果来看，经过掩膜法处理后信号40与130 Hz的峰值与未经过处理的信号相比明显削弱，并且80 Hz处明显突出。这是由于掩膜法中掩膜信号取的相关参数为瞬时幅值与瞬时频率，仿真信号的平均瞬时频率约为83 Hz，经掩膜法处理后，40与130 Hz处的峰值均被削弱。

图2 仿真信号f，g时频域图Fig.2 Simulation signal time-frequency domain of f and g

3 LMD-MS的基本原理

禹丹江等[20]在最小熵反卷积(minimum entropy deconvolution, 简称MED)分解中提出了一种确定掩膜信号的方法，而将其运用到LMD方法中时，可以对其进行适当改进。

由于LMD采用了基于极值点的包络求取的方式，其包络估计值误差经多次分解后会被放大，会出现模态混叠现象。MS方法采用加减后取平均的方法，可以减小由于多次平滑处理所积累的误差值，以此来消除模态混叠现象，同时消除噪声。

PF1=(PF++PF-)/2

(14)

在LMD-MS方法处理单故障的轴承信号中时，可以选择与原信号相关度最高的PF分量作为掩膜法处理的对象。

在故障信号中，故障冲击会周期性出现，所以在该频带内，频率能量均值会比其他频带处高。图3为式(14)仿真信号的频率能量均值图。

图3 仿真信号频率能量均值分布Fig.3 Simulation signal frequency energy mean distribution

图3中取各点左右15 Hz作频率能量平均，结果可以得到在45，75，135 Hz处的频率平均能量较高，将掩膜信号的平均瞬时频率调整为40与130 Hz时，结果如图4所示。

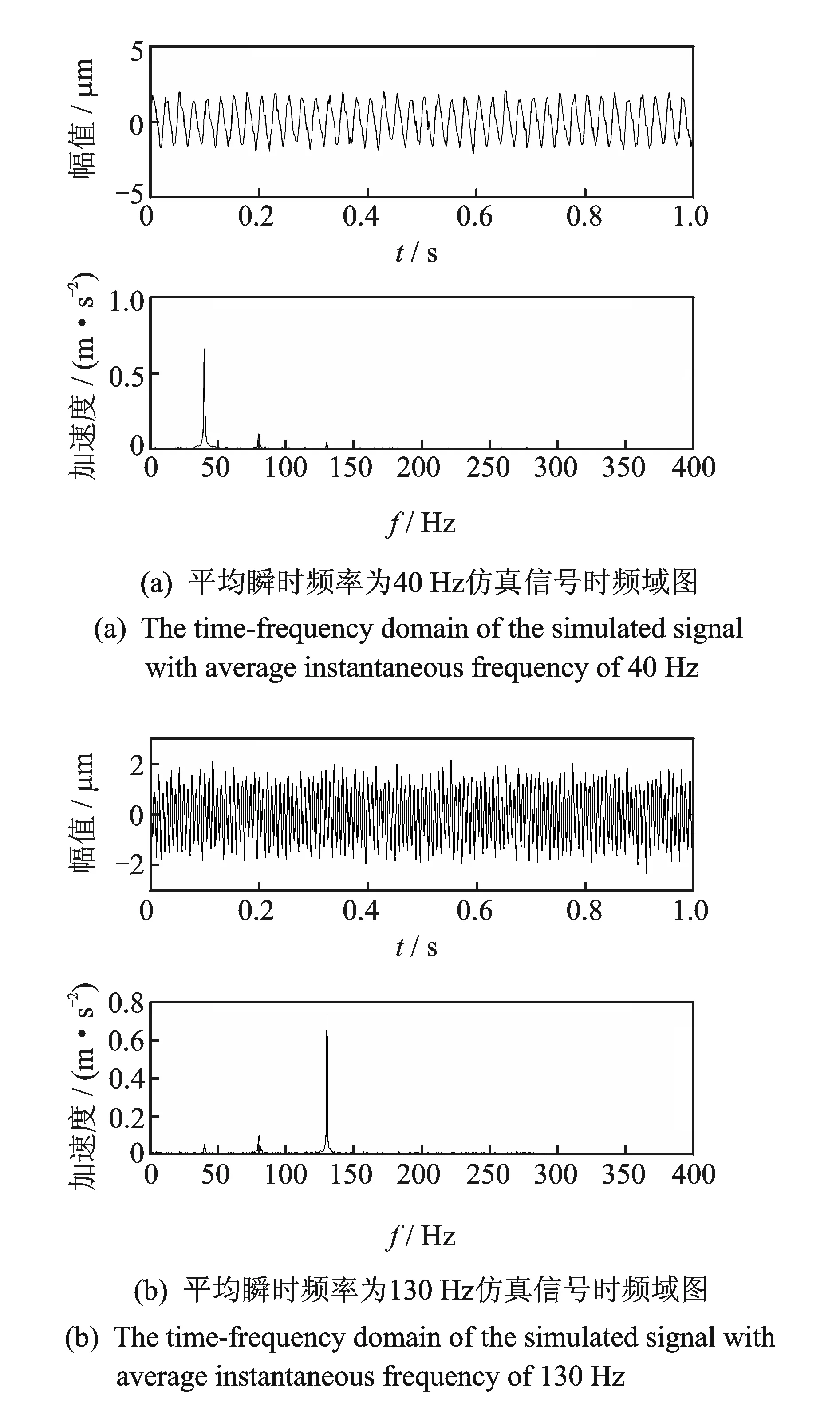
图4 平均瞬时频率为40，130 Hz的仿真信号时频域图Fig.4 The time-frequency domain of the simulated signal with average instantaneous frequency of 40 and 130 Hz

当平均瞬时频率为80 Hz的时频与图2基本相同，从图2，4的结果可见，掩膜信号的选取是关键，在使用掩膜法处理信号时，可以选取频率能量均值最高的频率作为选取掩膜信号的依据。

基于掩膜法和LMD的轴承故障诊断方法流程如图5所示。

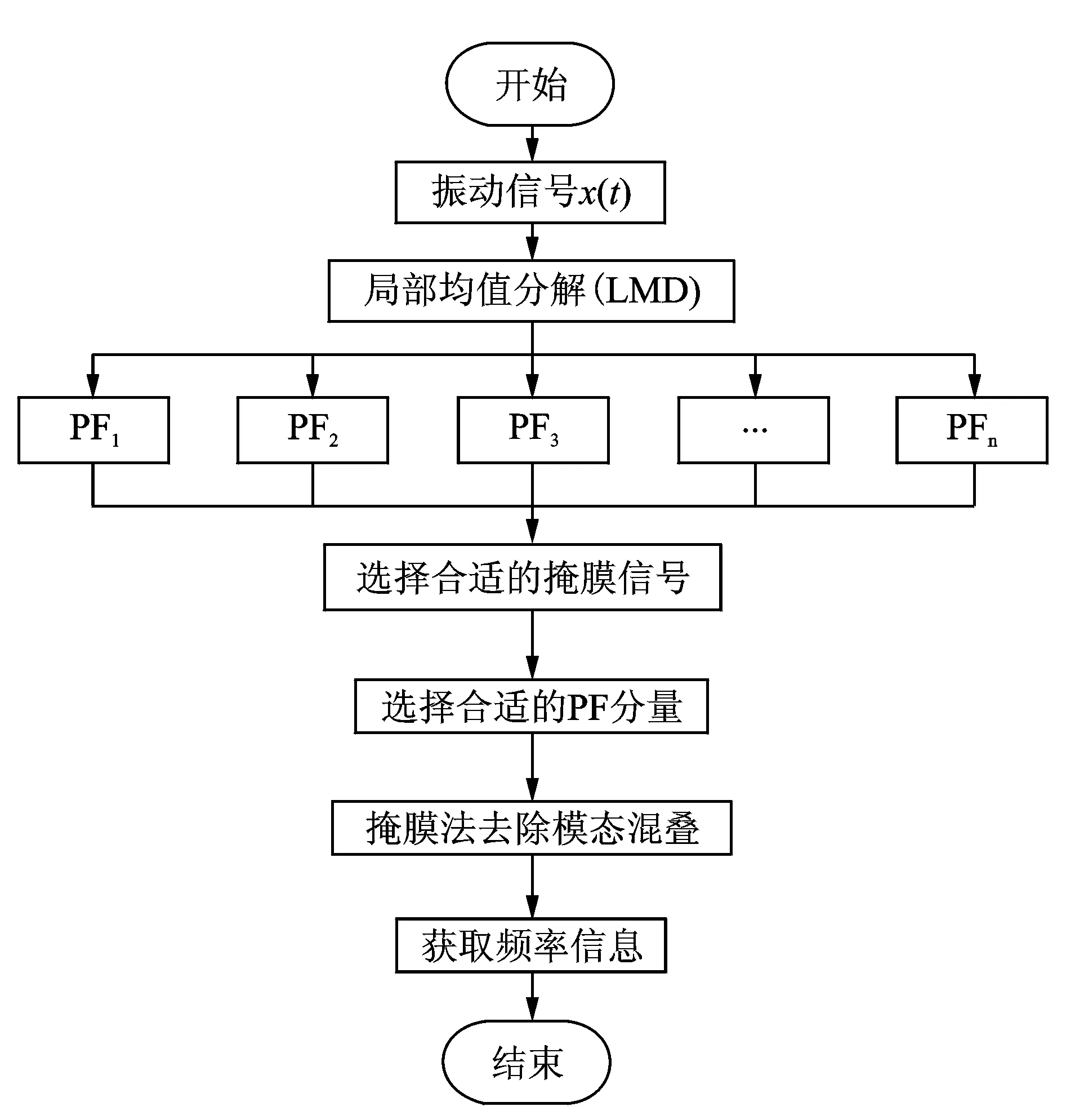
图5 LMD-MS流程图Fig.5 Flow chart of LMD-MS

4 仿真信号分析

为了验证LMD在噪声情况下的模态混叠现象，采用了式(15)的调制仿真信号，对应频率分别40，120和260 Hz，仿真信号对应的时域波形如图6所示。

x(t)=[1+0.8cos(240πt)+cos(520πt)]·

sin(80πt)+nnoise(t)

(15)

图6 仿真信号Fig.6 Simulation signal

图6中从上到下依次为正弦信号，噪声信号、两个余弦信号以及合成的仿真信号的时域图以及频域图，其中两个余弦函数都经过正弦函数调制。

在未用掩膜信号法对其进行处理直接进行LMD分解的PF分量时频域图如图7所示。其中第1层为PF1的时频域图，从频域图中可以明显的看出在120和260 Hz处有较高峰值，在40 Hz处有较低峰值。第2层为PF2的时频域图，在40和120 Hz处有明显峰值，同时由于噪声干扰，频谱中出现了许多虚假频率。第3层为PF3的时频域图，只在40 Hz处有较高峰值，第4层与第5层属于虚假分量，可以舍去。

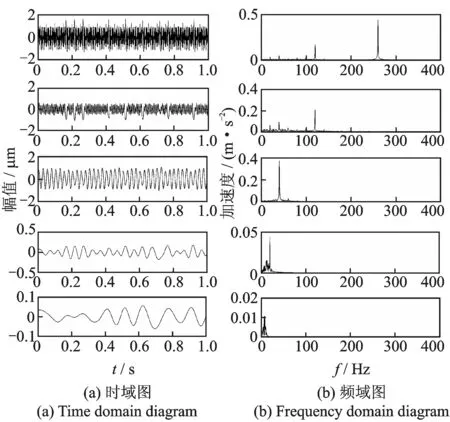
图7 仿真信号LMD分解结果Fig.7 Simulation signal′s decomposition results using LMD

由前3层PF分量对比可以得到120与260 Hz属于高频分量，40 Hz属于低频分量，但是120和260 Hz同时出现在了PF1的频谱中，40和120 Hz同时出现在了PF2的频谱中，证明发生了模态混叠现象。首先对仿真信号的平均频率能量均值参数进行计算并筛选所需频率信息。将频率值前后5 Hz作为频率能量平均长度，如图8所示。

图8 仿真信号频率能量均值分布Fig.8 Simulation signal frequency energy mean distribution

从图8所得结果可以得出40，120，260 Hz处的频率能量均值最高，根据这3个频率值选取掩膜信号。当掩膜信号的平均瞬时频率选为40 Hz时，对PF1，PF2，PF3处理都可以得到相应结果，但是对PF3处理所得结果最理想，而当掩膜信号的平均瞬时频率选为260 Hz时，对PF1进行处理显然不合理，所以在选择处理对象时，应根据实际情况调整。

文中选择的处理对象为：平均瞬时频率为40 Hz时对PF1处理，平均瞬时频率为120 Hz时对PF2处理，平均瞬时频率为260 Hz时对PF3处理。所得结果如图9所示。

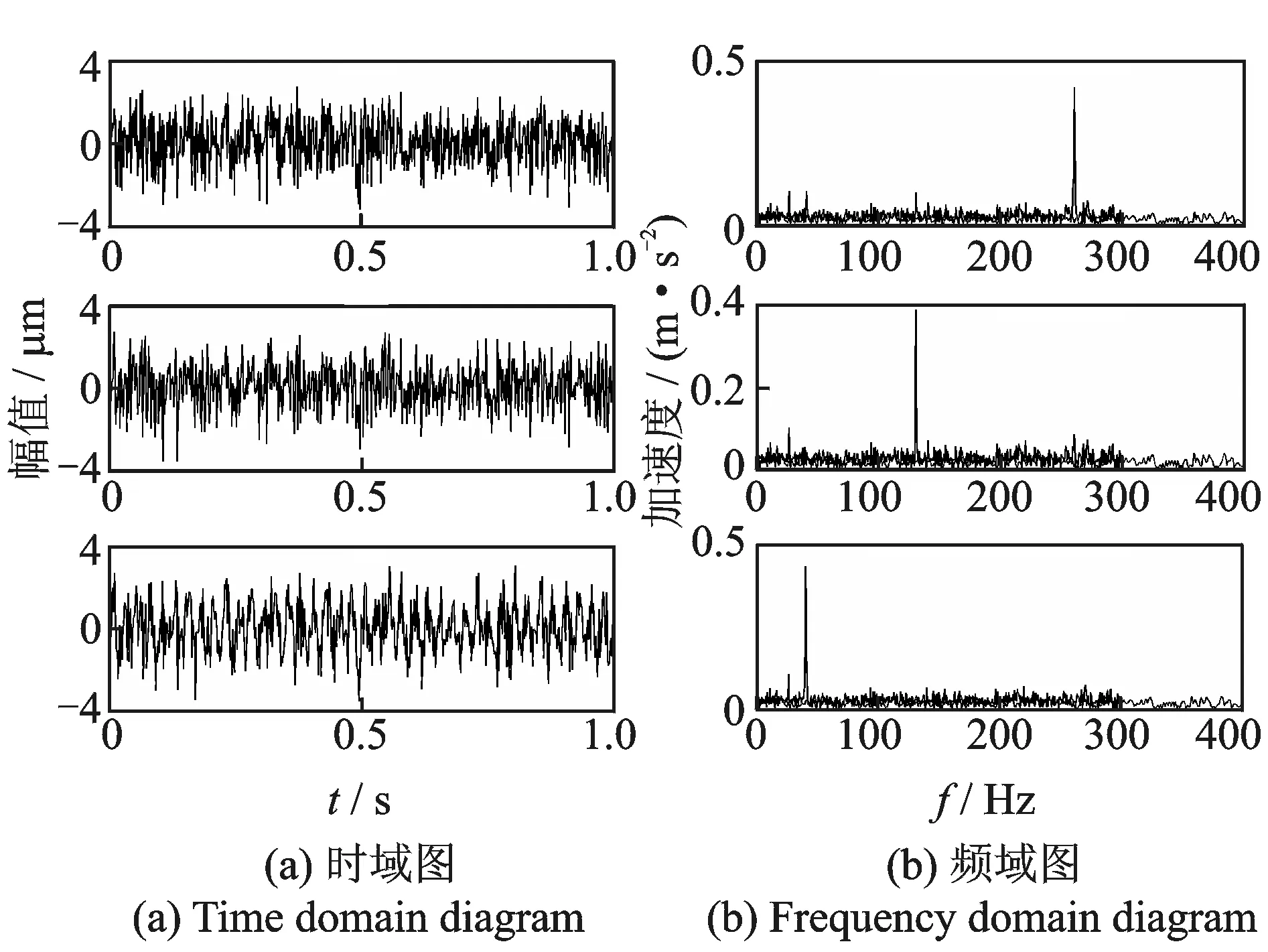
图9 仿真信号LMD-MS分解结果Fig.9 Simulation signal′s decomposition results using LMD-MS

前3阶PF分量中含有不同频率，虽然PF1中还有40与120 Hz频率成分存在，但是已经大幅削弱，由此可以确定掩膜法有效地削弱了仿真信号的模态混叠现象。

为了验证所提出方法的优势，引入变分模态分解(variational mode decomposition，简称VMD)方法作为对比。图10是仿真信号的VMD分解。由于VMD的结果受自身分解层数影响，分解结果容易失真。仿真信号组成为40，120，260 Hz，从VMD分解结果来看，其分解出的分量频率为54，130，335 Hz。与文中提出的LMD-MS方法相比，显然是文中方法分解出的结果较为精确，由此证明笔者提出的方法与其他分解方法相比有较强的优势。

图10 仿真信号VMD分解结果Fig.10 Simulation signal VMD decomposition results

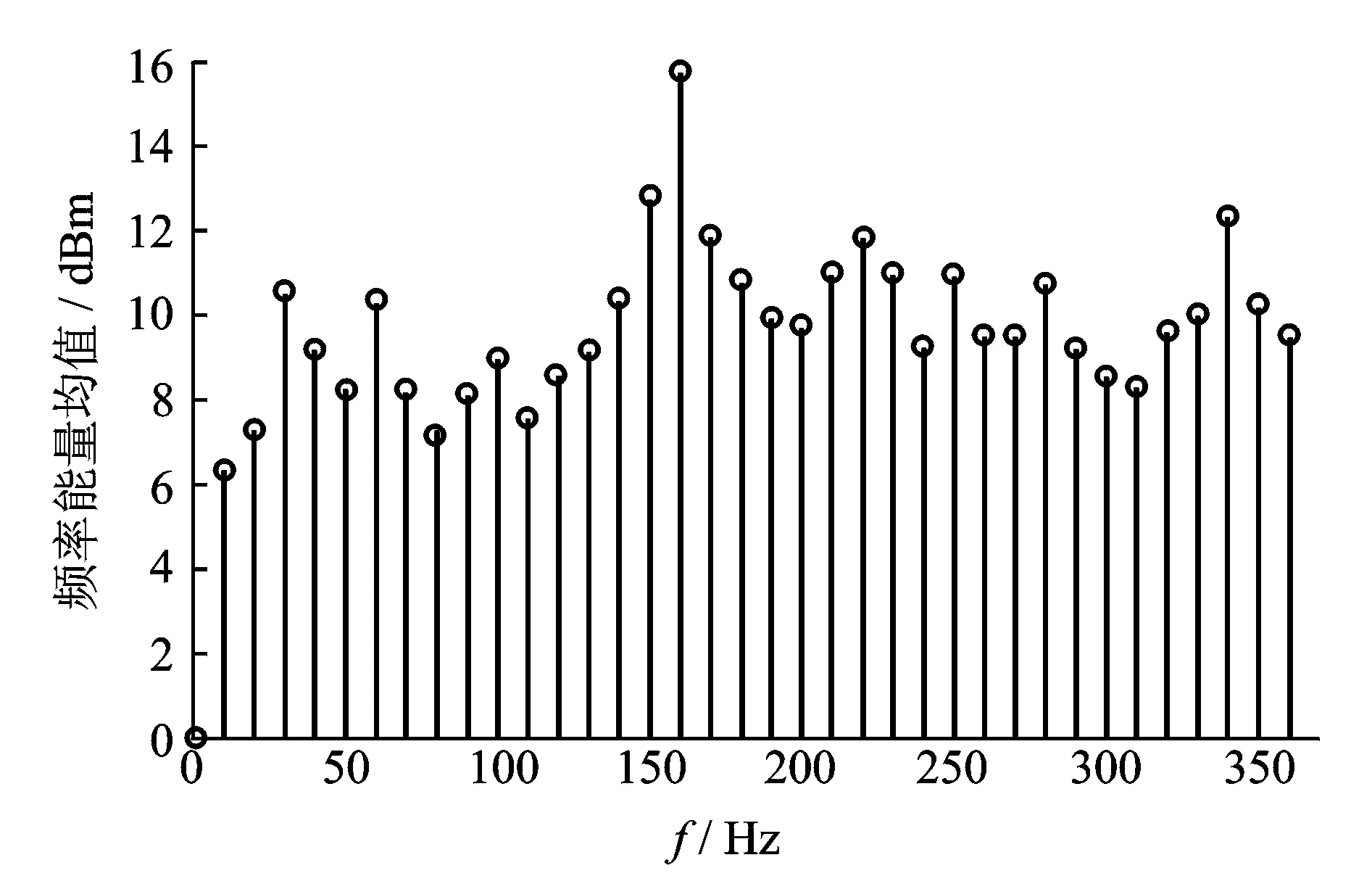
图11 原始信号频率能量均值分布Fig.11 Mean energy distribution of original signal frequency

5 LMD-MS滚动轴承故障信号分析

文中采用的是Case Western Reserve University(美国凯斯西储大学)故障轴承数据进行分析[21]，其中转速为1 750 r/min，采样频率为12 000 Hz，转动轴基频为29.1 Hz，计算后的内圈故障频率约为157.9 Hz，从采集到的数据中选取10 240个点进行分析研究。对原始信号的平均频率能量均值参数进行计算并筛选所需频率信息。将频率值前后5 Hz作为频率能量平均长度，如图11所示。图12为故障信号LMD分解时域波形图与包络分析结果，取与原信号相关较强的前3层PFs。

图11中，29，58 Hz处的频率能量均值较高，160 Hz的频率能量均值最高。由此确定掩膜信号。

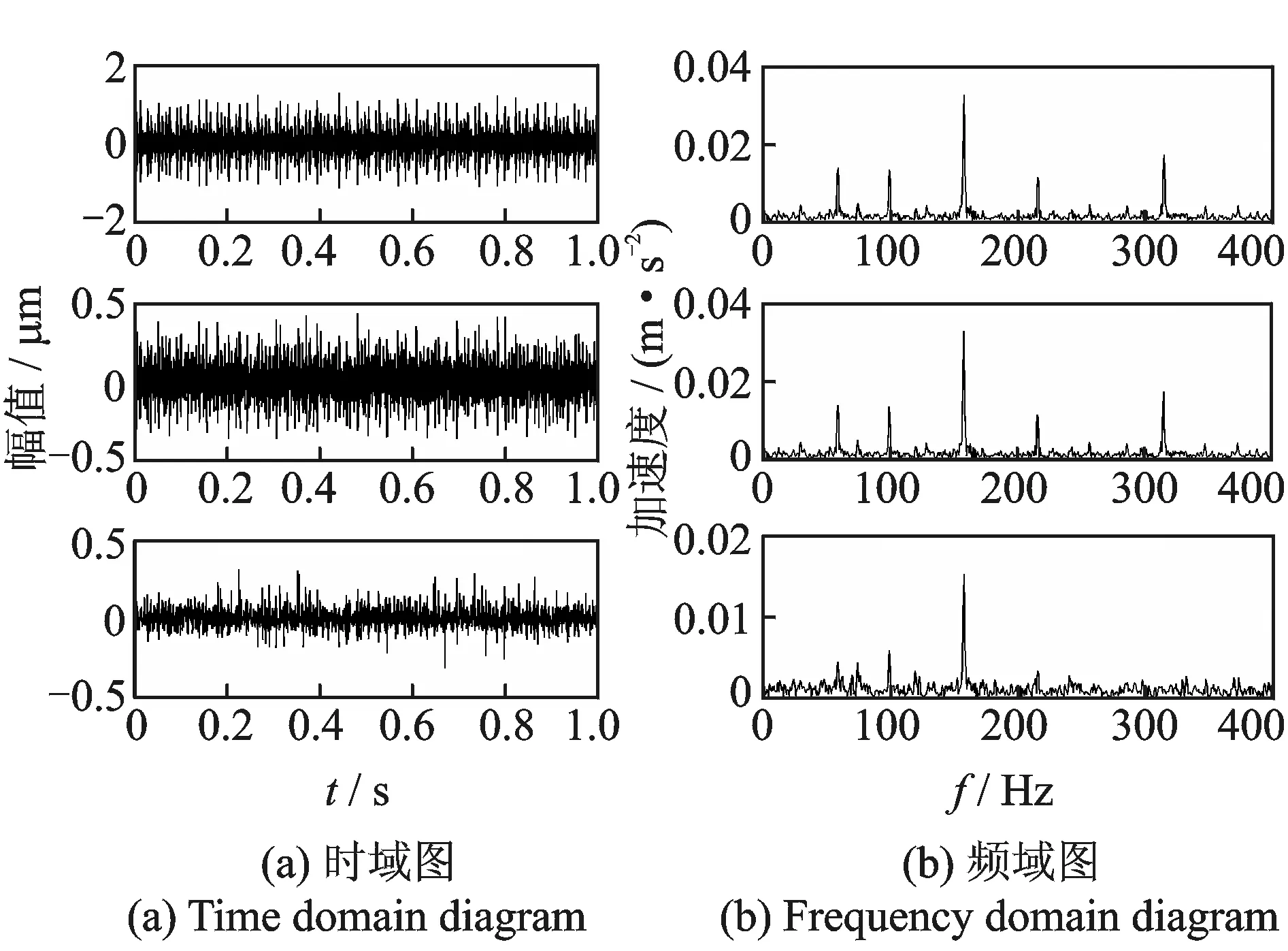
图12 原故障信号的LMD分解结果与包络分析结果Fig.12 Original fault signal′s decomposition results using LMD and envelope analysis

图11中，在内圈故障频率158.3 Hz处与其二倍频率316.6 Hz处有较高峰值，但是在转频29.1 Hz与二倍频率58.2 Hz处同时存在较高峰值，同时在98与210 Hz处也存在较高峰值，这是由于信号在传递过程中被调制所得虚假频率，PF2和PF3所得结果与PF1相似，由此证明发生了模态混叠现象。

从掩膜法处理后PF1分量的包络分析(见图13)对比结果来看，58，100 Hz处的峰值大幅削弱，图中较高峰值只出现在内圈故障158.1 Hz与二倍频316.2 Hz处，同时信号的幅值也有所减小，证明掩膜法具有一定消噪能力。经过计算，PF1的相关系数最高，所以选择PF1作为研究对象。在实际应用时可以选择相关系数最高的分量作为研究对象。

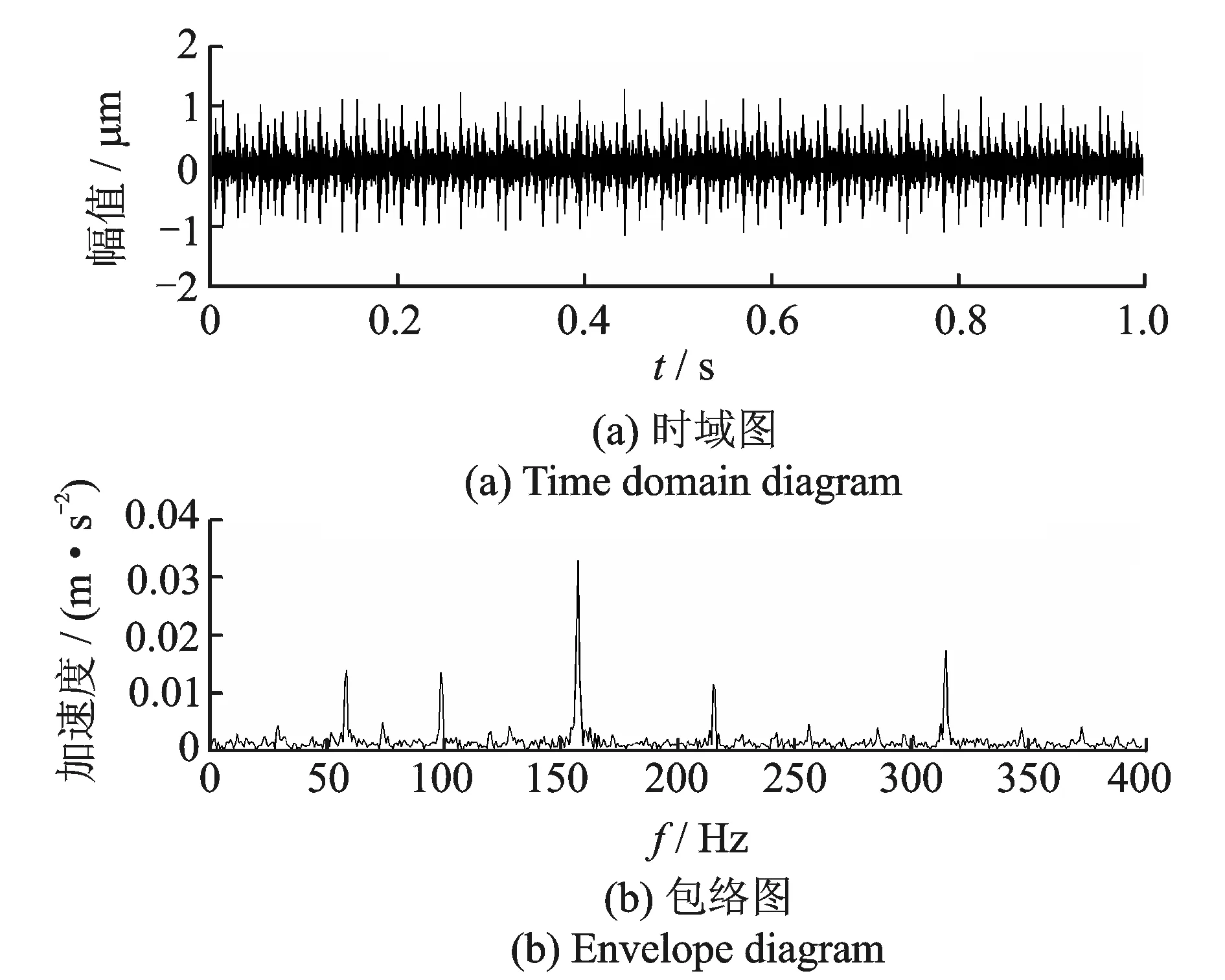
图13 掩膜法处理后的PF1时域图与包络分析图Fig.13 PF1 time domain diagram and envelope analysis using MS

与仿真信号相似，在此选择VMD作为对照方法，选择分解层数为3。VMD分解得到的3个分量如图14所示，频率峰值分别为50，120，355 Hz。明显没有分解出内圈故障频率157.9 Hz，这是由于VMD方法本身的性质决定的。所以再次证明了文中所用方法相比其他故障诊断方法具有一定的优越性。

图14 实测信号的VMD分解Fig.14 VMD decomposition of measured signal

从峭度角度研究LMD-MS的优化程度。PF1，PF2和PF3的峭度值分别从3.6，3.3和3.2增加至28.4，27.6和26.8，增加了近8倍。

从信噪比角度研究，根据信噪比求取公式

(16)

其中：S，N及L分别为信号的能量、噪声能量和信号长度；X(k)和X(k0)分别为k点处峰值与频谱中特征频率峰值。

掩膜法使用前与使用后信号在157.9 Hz处的信噪比提高了19.1%。

6 结束语

掩膜信号法对于强噪声背景下发生的模态混叠现象有较强的抑制作用，并通过实验验证了掩膜法具有一定的降噪能力。局部均值分解对故障信号有较强的分解分析能力，但是在强噪声背景下会失真，出现模态混叠等现象，难以得到有效的故障信息。笔者将掩膜法引入到LMD方法中，提出了一种将掩膜信号法与LMD相结合的的LMD-MS方法。使用LMD对信号进行分解，然后用掩膜信号法对PF分量进行处理，降噪并消除其模态混叠现象。利用仿真信号验证了方法的可行性，将实际信号使信噪比提高了19.1%，成功提取了轴承的微弱故障特征，为微弱故障特征提取提供了一种新的研究思路。