透平机械三转子四支撑轴系不平衡振动特性*

沈意平, 宾光富, 王 钢, 李学军

(湖南科技大学机械设备健康维护湖南省重点实验室 湘潭, 411201)

引 言

多转子轴系振动往往是影响发电、石化行业机械设备甚至是整个生产线安全稳定运行的重要因素，其中大多数振动故障是由转子质量不平衡直接引起或因平衡状态发生变化。统计资料表明：在现场发生的机组振动故障，属于转子质量不平衡的约占75%。尤其近年来国内发电行业采用高参数的N+1支撑超超临界汽轮机组。这种新型轴系具有结构紧凑、运行效率高等特点，但该轴系中相邻各转子振动特性相互耦合程度更高，造成轴系不平衡振动问题更为复杂[1]。国内外在轴系转子不平衡振动特性方面开展了大量研究[2-4]。文献[5]分析了双悬臂转子系统动力学特性及不平衡响应。苏引平等[6]研究了主跨支撑特性对三支撑轴系结构振动的影响。文献[7]进行转子不平衡量识别研究。陈景明等[8]研究了双转子-支撑系统不平衡故障识别法。文献[9]通过构建有限元模型分析转子不平衡特性，进而求取加重影响系数。崔亚辉等[10]分析了单支撑超超临界汽轮机轴系不平衡特性，发现相邻转子两临界转速附近的振动耦联性突出。以上多针对传统双支撑轴系开展不平衡振动特性仿真研究，而且较少涉及三转子四支撑这类单支撑轴系，尤其是转子振型不平衡对轴系振动影响鲜有报道。

因此，针对汽轮机、压缩机等透平机械三转子四支撑轴系结构特点，通过在轴系不同跨内施加一阶、二阶弯曲振型不平衡(即激励类型)，稳态同步响应分析得到轴系不同转速下涡动轨迹和振动响应，分析共振转速点和幅频、相频特性，揭示这种轴系各转子间不平衡振动特性和规律，为解决这类型机组多转子轴系不平衡振动问题提供参考。

1 轴系不平衡振动特性仿真分析

以三转子四支撑汽轮机轴系为对象研究其不平衡振动特性，其中轴系模拟结构参数如表1所示。

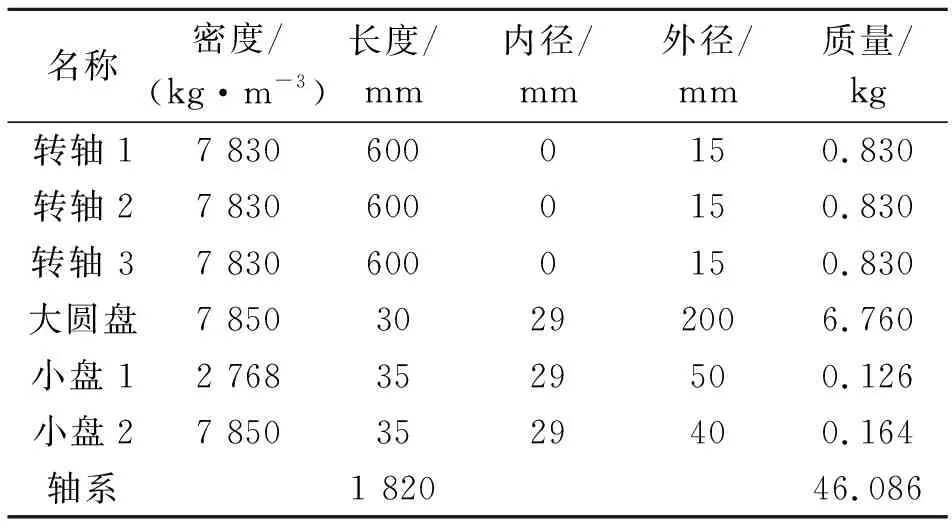
表1 轴系基本结构参数

1.1 轴系动力学有限元建模

根据转子动力学建模基本原则，采用有限元法构建轴系有限元模型如图1所示。为便于研究轴系中各跨转子的不平衡响应特性，在此不考虑轴承阻尼影响，即采用四个刚性支撑，分别对应节点2，6，13，20，其主刚度均设为5×104N/mm；刚性联轴器的径向刚度为1×105N/mm，角刚度为1×107N·mm/rad。轴系模型模型共21个节点，每个节点有(x,y,θx,θy)共4个自由度，由于节点7和8，14和15为联轴器同一位置点，各约束了1个自由度，故模型总计82个自由度[11]。

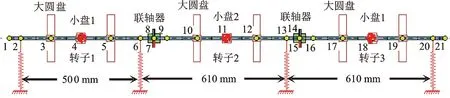
图1 三转子四支撑轴系有限元分析模型Fig.1 FEM for shafting with three-rotor and four-support

轴系临界转速(critical speed，简称Ncr)与振型分析结果如图2所示。

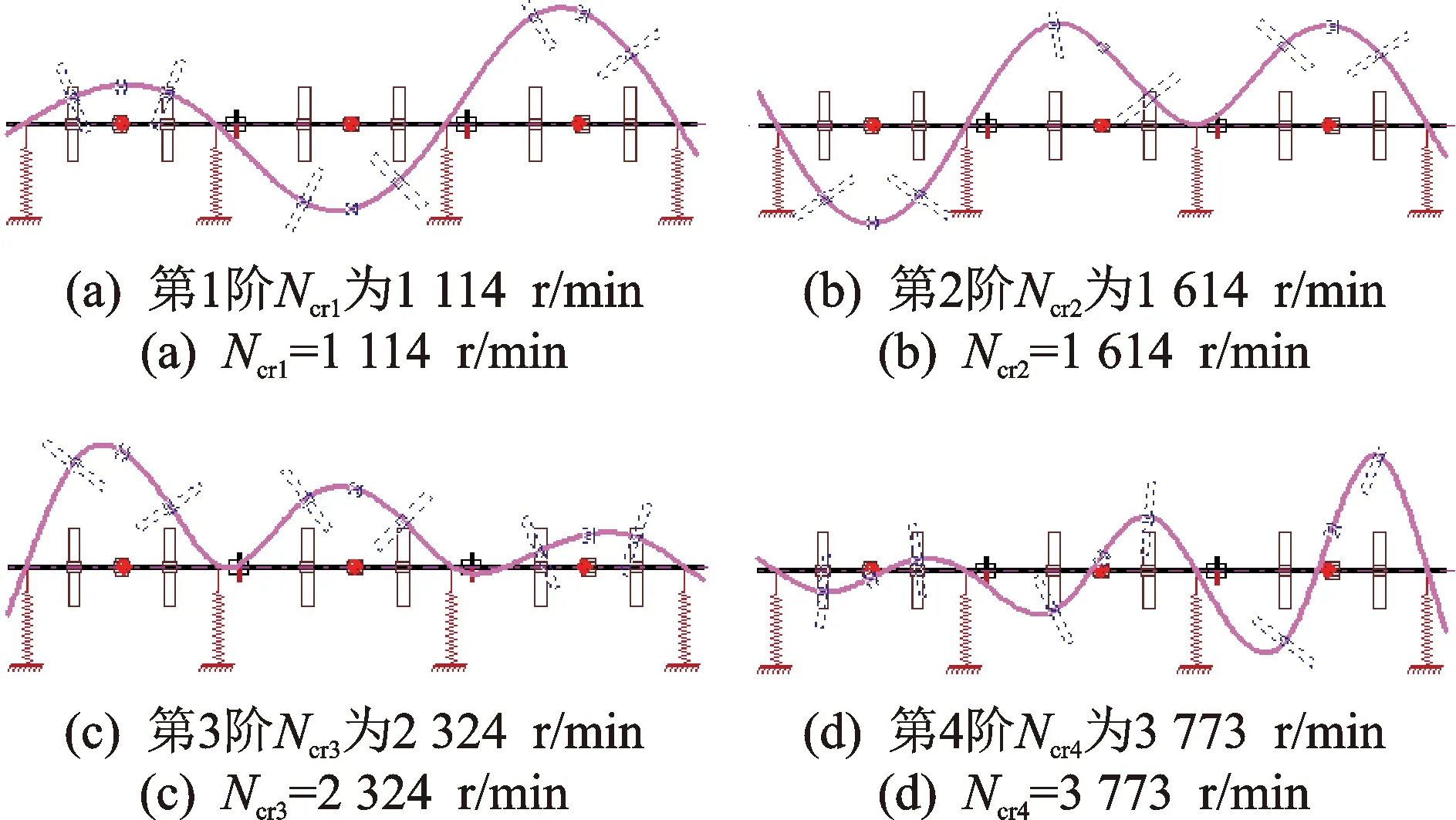
图2 前四阶临界转速及振型Fig.2 The first fourth critical speed and mode shape

显然可知：该轴系前四阶临界转速分别为：1 114, 1 614, 2 324, 3 773 r/min，其中对应前三阶轴系振型依次为第3跨、第2跨和第1跨转子的一阶弯曲振型，第4阶为第3跨转子的二阶弯曲振型。综合考虑转子结构特点，分别选择800，3 kr/min两个转速进行轴系临界转速前后振动特性分析。

1.2 轴系不平衡稳态响应分析

为研究不平衡激励类型对轴系振动的影响，在转子1两圆盘上分别施加大小为0.4 kg·mm的1阶、2阶弯曲振型不平衡(即同、反相不平衡)，分析轴系不平衡稳态响应，得到800和3 kr/min时轴系涡动轨迹，结果如图3, 4所示。

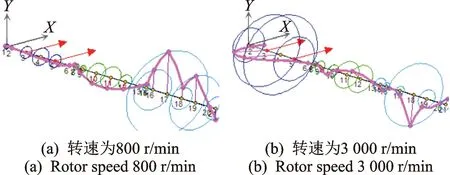
图3 转子1上同相不平衡激励下的轴系涡动轨迹Fig.3 Shaft response excited in-phase unbalance in rotor 1

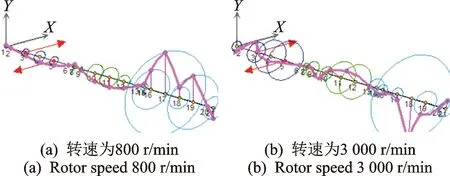
图4 转子1上反相不平衡激励下的轴系涡动轨迹Fig.4 Shaft response excited out-phase unbalance in rotor 1

结合图2中的轴系振型图，从图3和图4涡动响应轨迹可知：当转速为800 r/min时，轴系各跨转子为刚性转子，同相不平衡主要激起了轴系第1阶振型，也即此时轴系涡动主要以第3跨转子的1阶弯曲振型为主；当转速为3 kr/min时，即位于轴系3阶和4阶临界转速之间，轴系涡动轨迹主要由轴系的第3, 4阶振型混合组成，即转子1以1阶弯曲振型为主，而转子2和3则含有2阶弯曲振型成分。反相不平衡激励下轴系涡动则以四阶振型为主，转子1,2,3均表现为2阶弯曲振型。在转子2上进行同样分析与处理，得到转子2上不平衡激励下轴系涡动响应轨迹如图5和6所示。

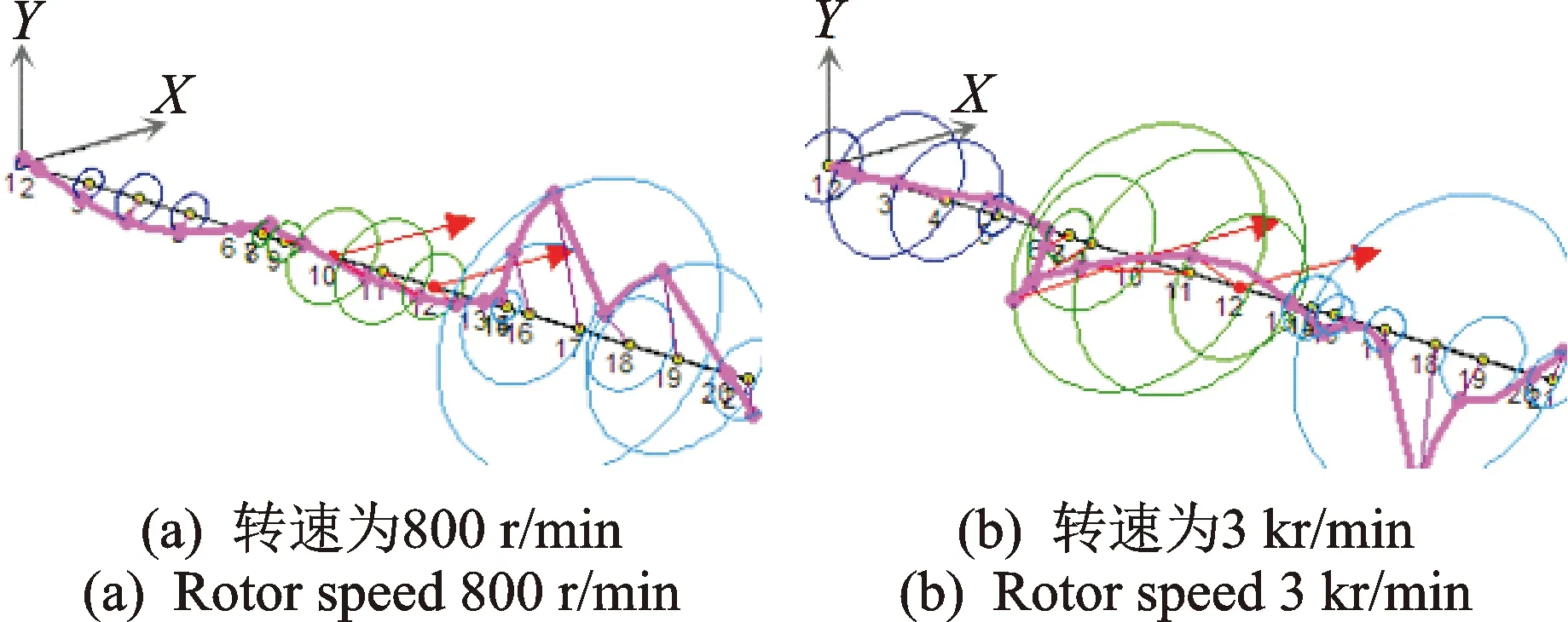
图5 转子2上同相不平衡激励下的轴系涡动轨迹Fig.5 Shaft response excited in-phase unbalance in rotor 2

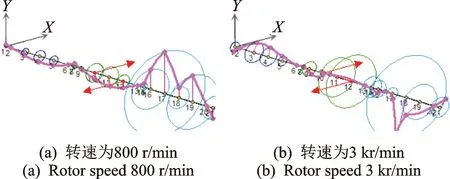
图6 转子2上反相不平衡激励下的轴系涡动轨迹Fig.6 Shaft response excited out-phase unbalance in rotor 2

同理，分析图5和图6可知：当转速为800 r/min时，轴系第2跨转子上的不平衡加重情形与第1跨转子基本类似；当转速为3 kr/min时，转子2上同相不平衡激励导致轴系涡动轨迹以轴系的三阶振型为主，即转子1，2，3均以一阶弯曲振型为主，但转子2和3挠曲变形较大，明显含有二阶弯曲振型分量。反相不平衡激励下轴系涡动轨迹则以轴系四阶振型为主，转子2和3则以二阶弯曲振型为主，而转子1则仍以一阶振型为主。同理，转子3上不平衡激励的分析结果分别如图7和8所示。

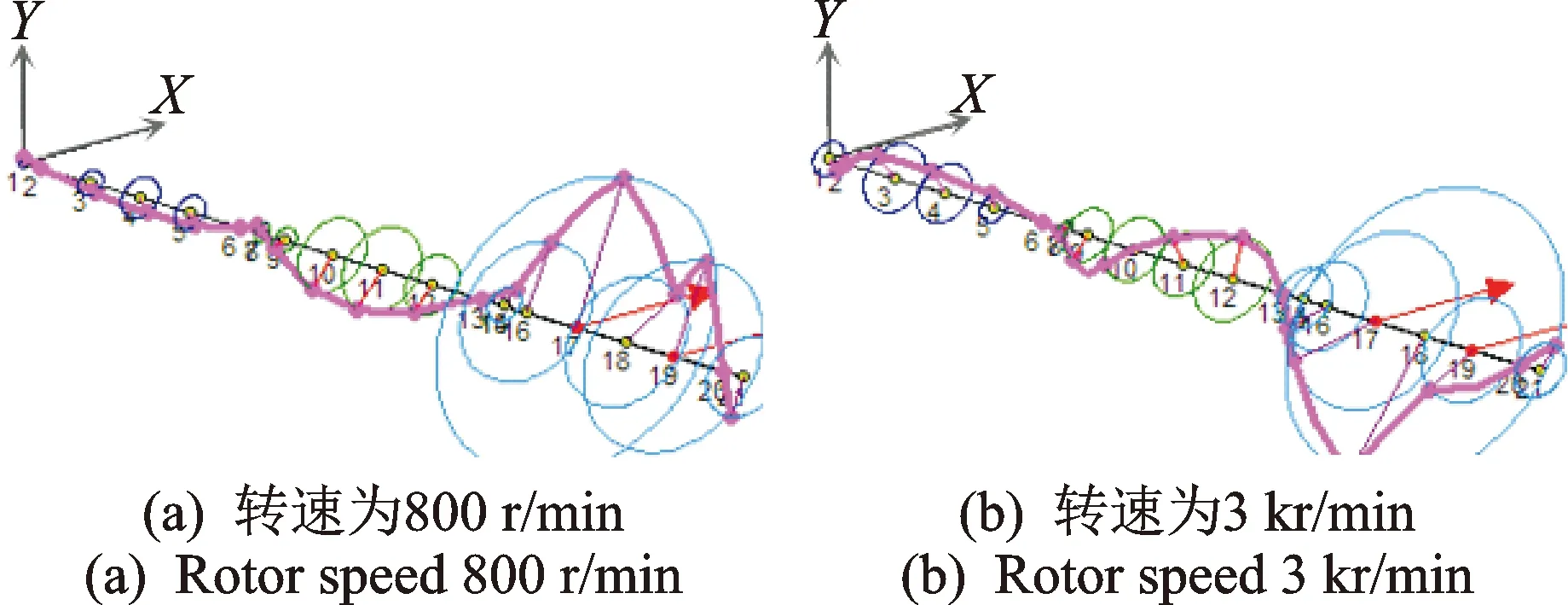
图7 转子3上同相不平衡激励下的轴系涡动Fig.7 Shaft response excited in-phase unbalance in rotor 3

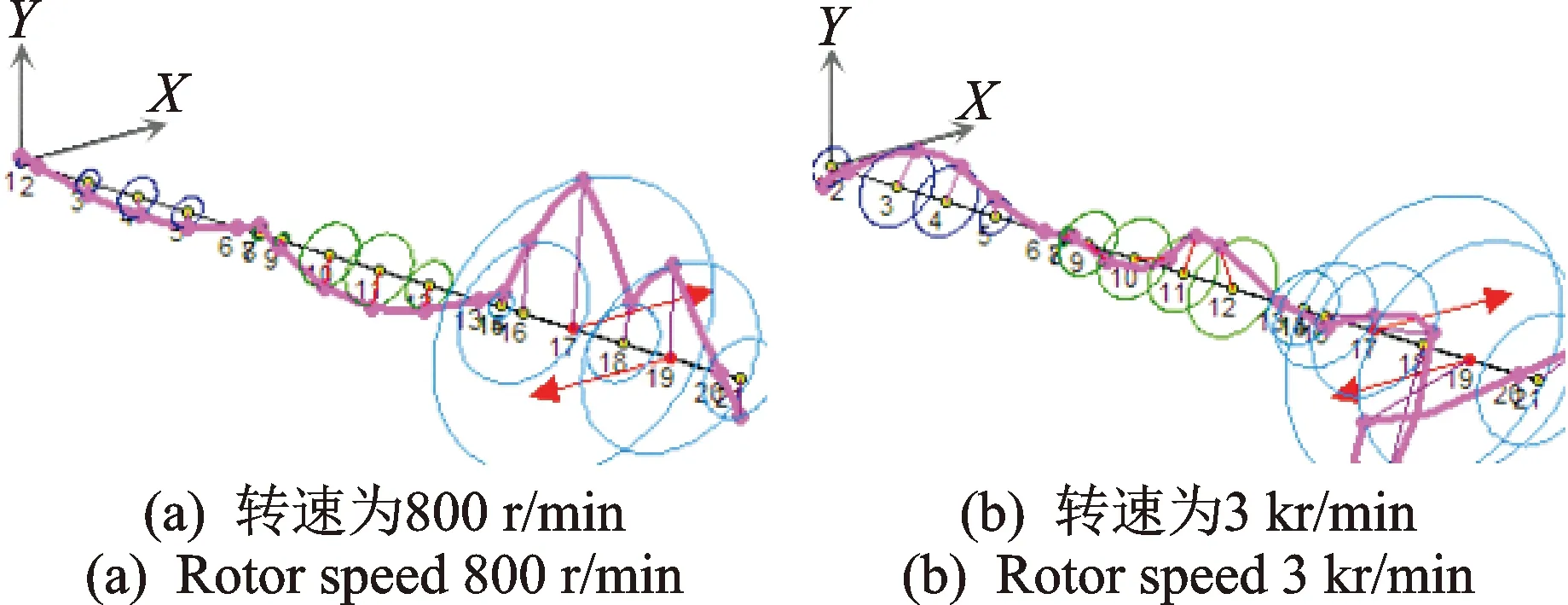
图8 转子3上反相不平衡激励下的轴系涡动Fig.8 Shaft response excited out-phase unbalance in rotor 3

同理，从图7和图8分析可知：当转速为800 r/min时，第3跨转子上不平衡激励引起的轴系涡动情况与第1跨转子基本一致，主要激起了轴系的第一阶振型；当转速为3 kr/min时，第3跨转子同相不平衡激励下的轴系涡动则主要由轴系第3,4阶振型联合决定，即转子3的涡动以一阶弯曲振型为主，而转子2以二阶弯曲振型为主，转子1以一阶弯曲振型为主。反相不平衡激励下轴系涡动则以轴系四阶振型为主，转子3和2以明显的二阶弯曲振型为主，而转子1则以一阶弯曲振型为主。

2 轴系不平衡振动特性实验

为验证这类轴系不平衡振动响应特性，设计了透平机械三转子四支撑轴系模拟实验台，该轴系的支撑采用HM20N卧式硬支撑动平衡机摆架，内嵌灵敏度310 mV/(mm·s-1)的SV16振动速度传感器来测量转子水平振动。轴系采用电机皮带驱动模式。采用LMS测试系统进行数据采集与处理，其中采集的分析频率带宽设为512 Hz，分辨率为0.5 Hz，谱线数为1 024。

2.1 轴系不平衡特性实验方案

针对表1所述三转子四支撑轴系中基本结构参数，搭建的轴系模拟转子实验台如图9所示。轴系转子采用双圆盘结构，参数如表1所示。其中，支撑摆架采用两个对称滚轮支撑转轴，将3#和5#标高降低，只留下1#,2#,4#和6#共4个摆架支撑轴系，各转子间通过刚性联轴器刚性相连。

图9 三转子四支撑轴系实验台Fig.9 Shafting rig with three-rotor and four-support

为消除实验过程中由于转子材质不均匀、制造装配等误差造成的原始不平衡以及驱动系统对实验转子的影响，根据转子不平衡激励与振动响应的线性关系，将测试的加重螺钉振动响应与初始振动响应通过矢量运算相减，得到仅由加重螺钉引起的转子振动响应。因此在经过单转子高速动平衡后，再刚性连成轴系，测得初始状态下轴系四支撑的升速工频振动情况如图10所示。

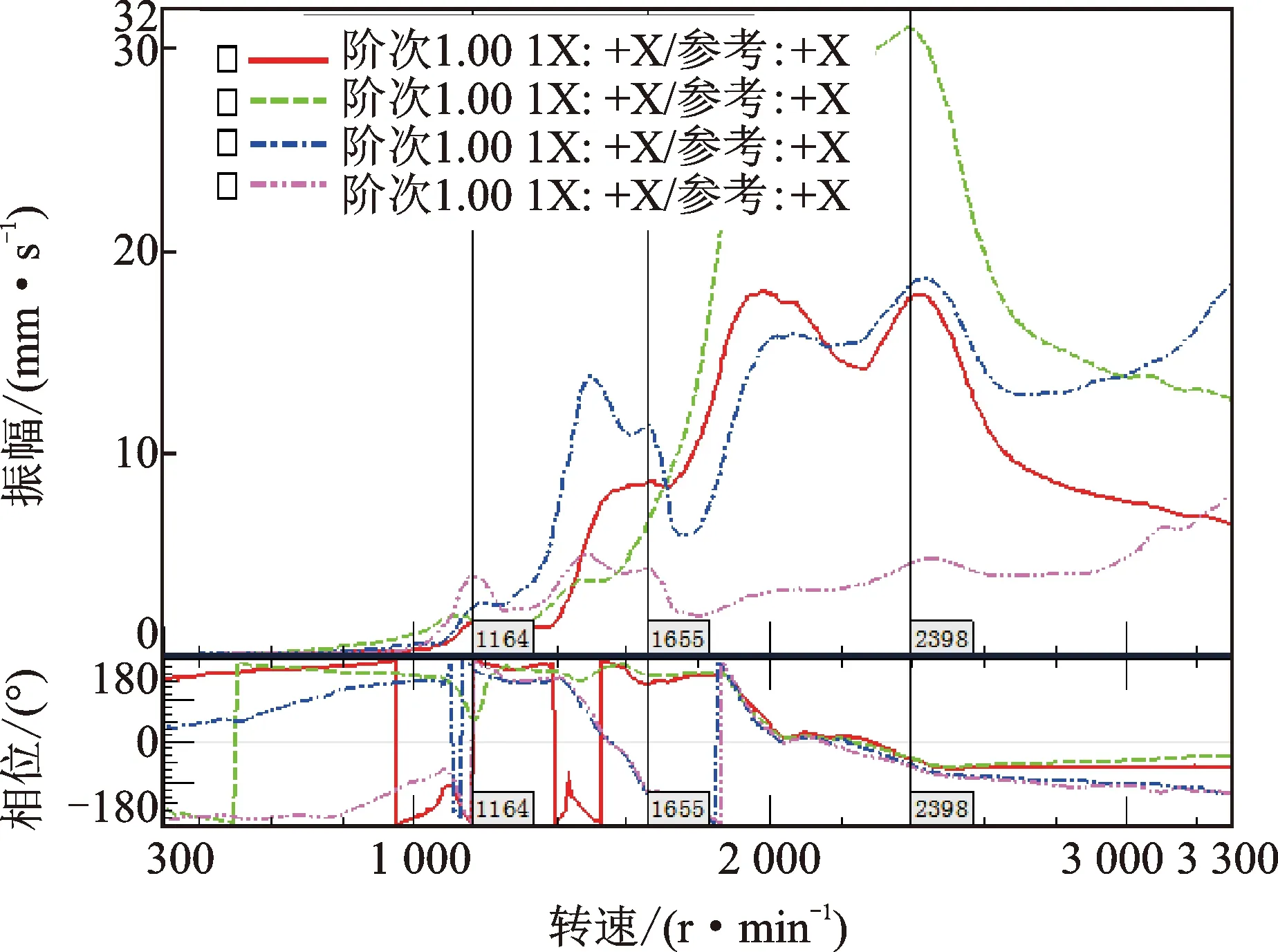
图10 轴系的初始振动Fig.10 Initial vibration of shafting rig

图中“阶次1.00 1X：+X”表示支撑1处水平方向X振动速度基频分量，“参考：+X”表示参考的转速探头为水平方向X，其他曲线含义依此类推。从图10可知该三转子四支撑轴系的前3阶临界转速约为1 164, 1 655和2 398 r/min，分别对应轴系第3,2,1个转子的临界转速。工程上，通常采用临界转速值来检验转子动力学建模的质量，显然本研究中实测值与1.1节仿真计算值相对误差在5%以内，说明仿真建模参数合理[12]。

2.2 三转子四支撑轴系不平衡振动响应实验

首先测量经动平衡过的轴系初始振动，然后在转子1两大圆盘的0和180°上分别加5 g同相和反相不平衡配重螺钉，以模拟转子1上的一阶和二阶振型不平衡，测量转子在300～3 300 r/min下三支撑的工频振动，经处理得到转子1配重的加重响应如图11所示。同理，可得到转子2、3配重后的加重响应如图12，13所示。其中“1-T-1X”表示转子1上两大圆盘加同相不平衡激励时，支撑1的水平振动；“1-F-1X”为加反相不平衡激励时，支撑1的水平振动，其他依此类推。

从图11～13中实测的加重响应数据，可分析各转子不平衡对三转子四支撑轴系振动的影响如下：

在轴系各转子跨内加同相螺钉时，即施加的是一阶弯曲振型不平衡激励，所加螺钉跨内两支撑工频振动依次在1 200，1 650，2 450 r/min左右有明显振幅峰值，相位约有180°突变，且一直同相，显然依次激起了转子3，2，1的一阶弯曲振型；加反相螺钉时，即施加二阶弯曲振型不平衡激励，有同样的峰值现象，相位也有突变，但对应的峰值比加同相螺钉时的峰值要小很多，且随着转速升高，两支撑振幅明显上升，相位也一直反相，这说明在低转速下以转子一阶弯曲振型为主，高转速下以转子二阶弯曲振型为主。这些现象均与单转子跨内不平衡加重响应特性相似。

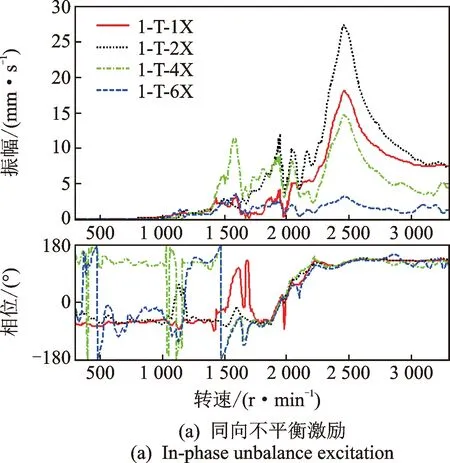
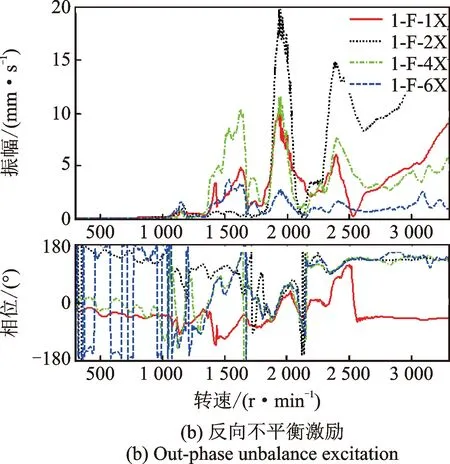
图11 三转子四支撑轴系在转子1配重的加重响应测试Fig.11 Weighted response of rotor 1# from shafting with three-rotor and four-bearing

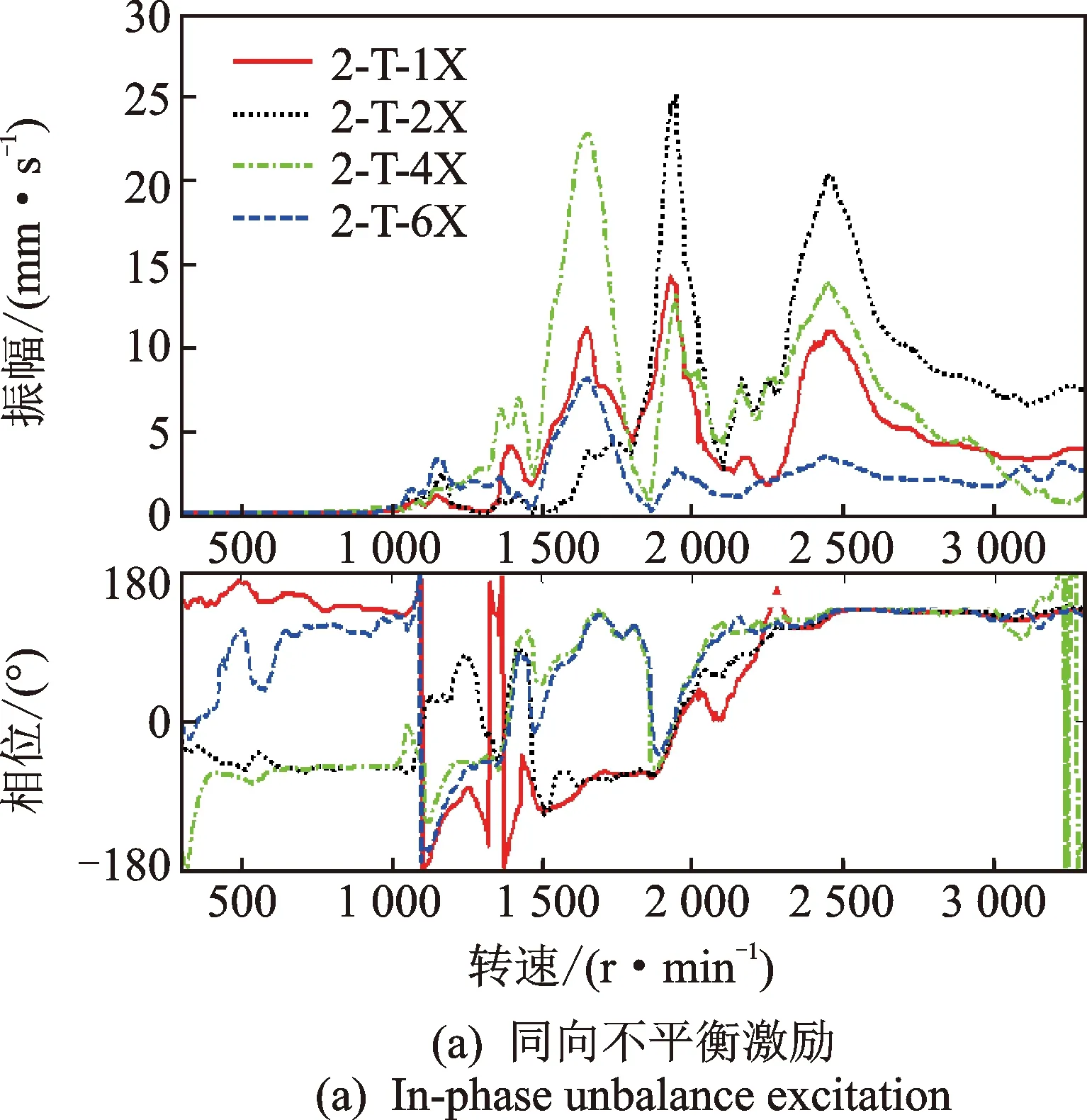
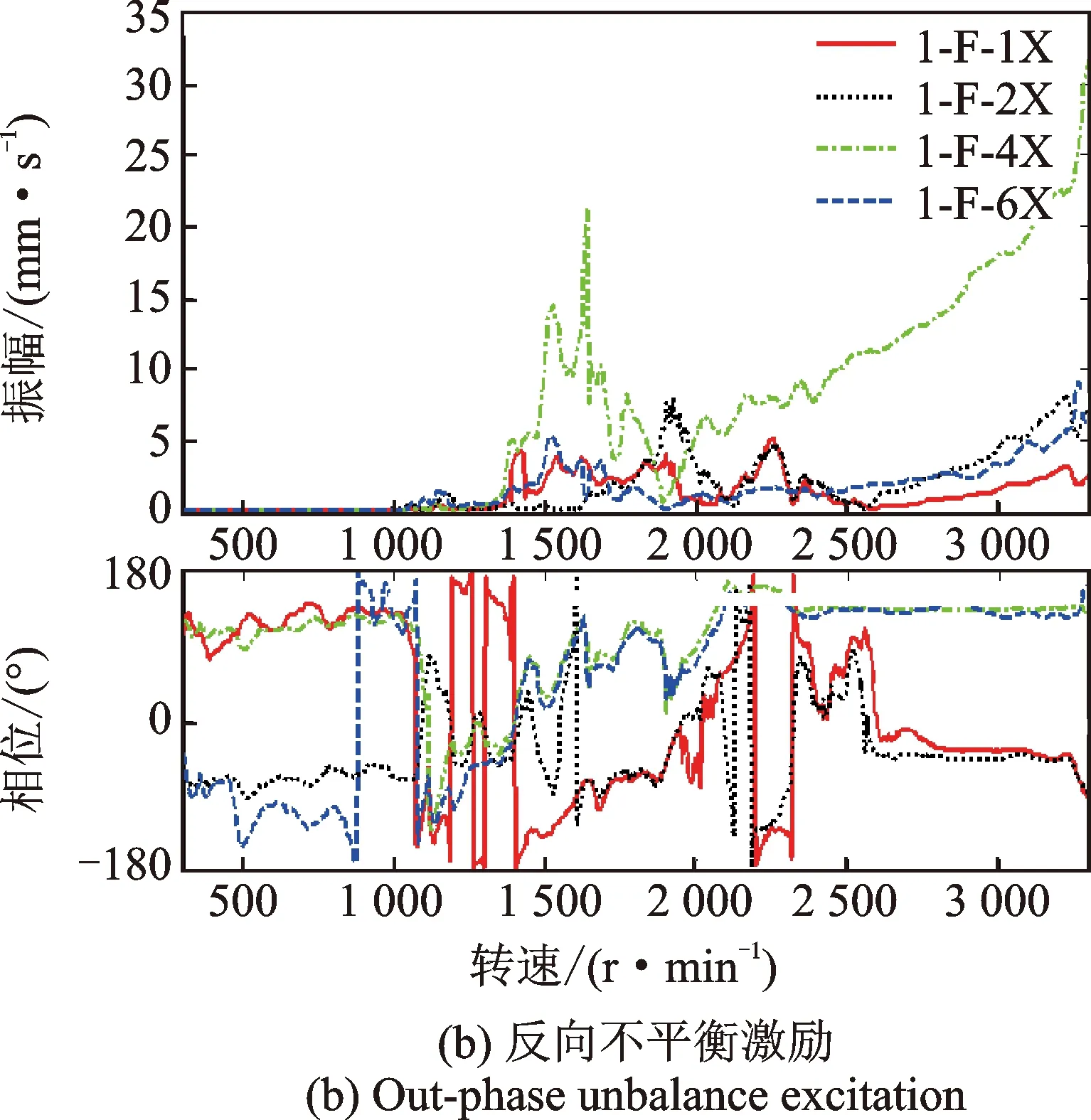
图12 三转子四支撑轴系在转子2配重的加重响应测试Fig.12 Weighted response of rotor 2# from shafting with three-rotor and four-bearing

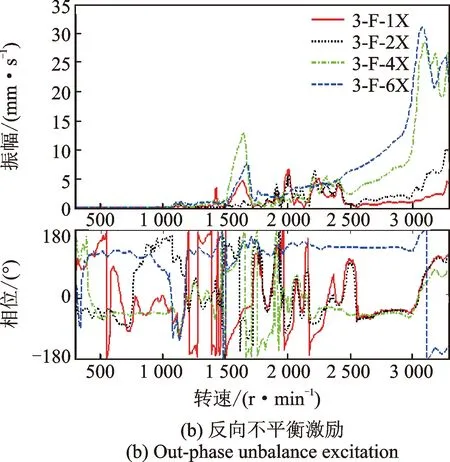
图13 三转子四支撑轴系在转子3配重的加重响应测试Fig.13 Weighted response of rotor 3# from shafting with three-rotor and four-bearing

在轴系转子1上加重时，支撑2和3的振动相位在1650 r/min之前为反相，之后则为同相。支撑3和4的振动相位在1 200 r/min之前为反相，之后则为同相，且支撑2,3,4的振幅依次减小；在转子2上加重时，支撑1和2的振动相位在1650 r/min之前为反相，之后则为同相。支撑3和4的振动相位在1200 r/min之前为反相，之后则为同相，且支撑4的振幅较支撑3的明显偏小；在转子3上加重时，支撑1和2的振动相位在2 450 r/min之前为反相，之后则为同相。支撑2和3的振动相位在1 650 r/min之前为反相，之后则为同相，且支撑1,2,3振幅依次增大有规律。显然，这些现象与转子外伸端不平衡振动特性及轴系振动传递特性有关。

在轴系各跨转子上加重，各支撑振动除了临界转速点外均存在多个峰值点，尤其是在1 900 r/min左右非常明显，且加同相不平衡螺钉比反相不平衡螺钉时表现更为突出，这可能与转子2和3结构相似，相互间强耦合影响有关，这时需结合相频曲线来综合判断临界转速点。由于该轴系实验台支撑为绝对刚性，阻尼值很小，难以抑制转子振动，这也可从各支撑振动相位存在较大波动加以判断。这些现象均很少在单转子不平衡振动中出现。

3 结 论

1) 三转子四支撑轴系各转子跨内加重振动响应由轴系振型和激励类型共同决定。在800 r/min低转速时，不管不平衡激励类型如何，轴系涡动始终以轴系的一阶振型为主；在3 kr/min高转速时，加同相不平衡激励则主要以该跨转子的一阶弯曲振型为主，而加反相不平衡激励则主要以该跨转子的二阶弯曲振型为主。

2) 三转子四支撑轴系具有转子外伸端振动特性。由于单支撑轴系特殊结构，轴系各支撑振动表现出振动特性与单转子外伸端相似，即在转子跨内进行不平衡激励，则转子的一个支撑与其跨外相邻支撑的振动相位在该跨转子一阶临界转速之前为反相，之后则为同相。

3) 三转子四支撑轴系转子间振动影响明显，有可能产生多个振动峰值。由于轴系转子间结构相互耦合，除了共振点外，不平衡激励下轴系振动会产生多个新的振动峰值，这时需结合相频曲线进行综合判断。本研究的结论可为汽轮机组、压缩机组等这类多转子轴系不平衡振动问题提供参考，尤其是为轴系动平衡中振型不平衡型式判断和关注测点相互影响分析提供依据。同时，今后还需进一步考虑油膜轴承、轴承标高、联轴器等因素对这类轴系不平衡振动响应特性的影响。