应用EMD和倒包络谱分析的故障提取方法*

孙 伟， 李新民， 金小强， 黄建萍， 张先辉

(中国直升机设计研究所直升机旋翼动力学重点实验室 景德镇, 333001)

引 言

滚动轴承是机械设备中应用最为广泛的零部件之一，机械故障大多数是由轴承引起，因此对滚动轴承的故障诊断方法研究具有重大意义。若滚动轴承工作在复杂状况下，当出现故障时，易出现振动信号调制现象，通常采用的快速傅里叶变换方法难以有效识别。倒频谱分析是一种有效的轴承振动信号监测诊断方法，其优点是对分离和提取难以识别的调制性成分非常有效[1]。若滚动轴承故障发生在早期，引起的振动信号调制现象非常微弱，所形成的周期性边频带分量幅值很小[2]，且受到随机噪声的干扰，容易被掩盖，导致故障不易识别[3]，因此单一使用倒频谱方法很难提取强背景噪声下滚动轴承早期故障特征。

为了解决上述问题，将MED和倒包络谱分析相结合，提出了一种基于MED与倒包络谱分析的故障特征提取方法。MED方法是由Wiggins提出的一种新的信号预处理方法，能够对振动信号进行降噪，同时增强信号中的冲击特征[4]，包络谱分析方法可通过希尔伯特变换对信号进行进一步降噪[5]，因此，先对信号进行MED降噪处理，然后计算包络信号，再对包络信号进行倒频谱分析，能够更有效地提取出故障特征信息。

1 MED方法

MED方法原理是利用最小熵能增强尖锐脉冲特征的特性来设计最优滤波器，具体原理如下[6-7]。

滚动轴承振动信号为

y(i)=h(i)*x(i)+α(i) (i=1,2,…,N)

(1)

其中：y(i)为振动信号；h(i)为传递函数；x(i)为冲击特征信号；α(i)为噪声信号。

设计逆滤波器f(i)，使得经过f(i)滤波后的y(i)能够恢复x(i)的冲击特征，即使熵值最小。

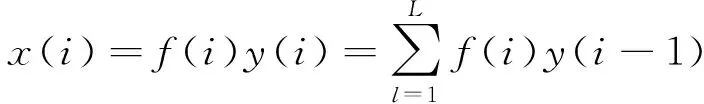
(i=1,2,…,N)

(2)

其中：L为f(i)的长度。

解反褶积，利用f(i)使y(i)恢复原有相关信息，使熵值最小，即

(3)

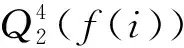
(4)

联合式(2)可得

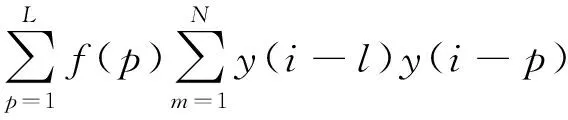
(5)

式(5)也可表示为

b=Af

(6)

其中：A为振动信号y(i)的L×L自相关矩阵。

b表示为

(7)

其中

(8)

式(5)经迭代可以得到逆滤波器矩阵为

f=A-1b

(9)

2 倒包络谱分析

2.1 倒频谱分析

倒频谱能将信号频谱图上成簇的边频带谱线简化为单根的谱线，易于观察。

倒频谱分析主要有两种方法：复倒谱分析和实倒谱分析。倒频谱分析定义[8-9]如下。

给定的信号为x(t)，其功率谱函数为Sx(f)，用Cp(τ)来表示功率谱Sx(f)的倒频谱，有

Cp(τ)=F-1{lg[sy(f)]}

(10)

倒频谱Ca(τ)为

Ca(τ)=|F-1{lg[sy(f)]}|

(11)

其中：F-1{}为傅里叶逆变换；τ为倒谱时间变量。

2.2 倒包络谱分析

包络信号的核心是对信号进行Hibert变换，相当于对信号进行了一次滤波处理[10],可以有效提高信噪比。对包络信号进行倒频谱运算，求得倒包络谱，可以减少噪声对倒频谱分析方法的影响。

对信号进行倒包络谱分析的步骤如下。

1) 对信号x(t)进行Hilbert变换，即

(12)

2) 构造解析信号z(t),即

z(t)=x(t)+jH[x(t)]

(13)

3) 解析信号z(t)求模，即得信号的包络B(t)

(14)

4) 对包络信号B(t)作倒频谱分析即可得到倒包络谱。

3 基于MED和倒包络谱分析的故障提取

滚动轴承工作在复杂状况下，易产生振动信号调制现象，而且调制现象易受到噪声的干扰，严重影响故障特征提取，基于MED和倒包络谱分析的故障特征提取方法，具体步骤如下。

1) 对故障信号进行MED预处理，在降噪的同时，增强信号中的冲击成分；

2) 利用Hilbert包络对降噪后的信号进行解调，得到包络信号，进行进一步降噪；

3) 对包络信号做倒频谱分析，得到MED降噪后的倒包络谱；

4) 将轴承故障特征频率理论值的倒数与倒包络谱中峰值谱线进行对比，最终判断故障类型。

采用洛阳轴承厂滚动轴承试验台进行试验，如图1所示。试验台主要由轴承疲劳加载试验机和加速度传感器等组成，滚动轴承结构参数如表1所示。试验过程中，为了模拟局部故障，采用电火花单点对轴承进行不同程度的刻蚀，形成内圈故障、外圈故障和滚珠故障，故障深度为0.4 mm,宽为1.2 mm。

图1 轴承故障诊断试验系统Fig.1 Fault diagnosis test system of bearing

参 数数值滚球直径d/mm9.525滚珠中心距D/mm374.326滚珠数N95滚珠接触角α/(°)30轴转速n/(r·min-1)219

转速及各故障频率计算公式如下[11]。

转速频率

fr=n/60

(15)

内圈故障频率

(16)

外圈故障频率

(17)

滚珠故障频率

(18)

采样频率为5 kHz，根据式(15～18)，计算转轴基频fr=3.65 Hz，内圈故障频率为fb≈177.20 Hz(对应倒频谱上时间点为5.6 ms)，外圈故障频率为fo≈169.55 Hz(对应倒频谱上时间点为5.9 ms)，滚珠故障频率fi≈71.69 Hz(对应倒频谱上时间点为14 ms)。

3.1 内圈故障

内圈故障信号频谱见图2，从图2上可以看出在内圈故障频率177.20 Hz处幅值已完全被噪声掩盖，无法提取故障特征频率。

采用本方法对内圈故障信号进行分析，首先采用MED方法对内圈故障数据进行预处理,如图3所示。与图2相比，图3中故障频率177.20 Hz处的幅值有所增强，但并不突出，而且仍然含有大量噪声。

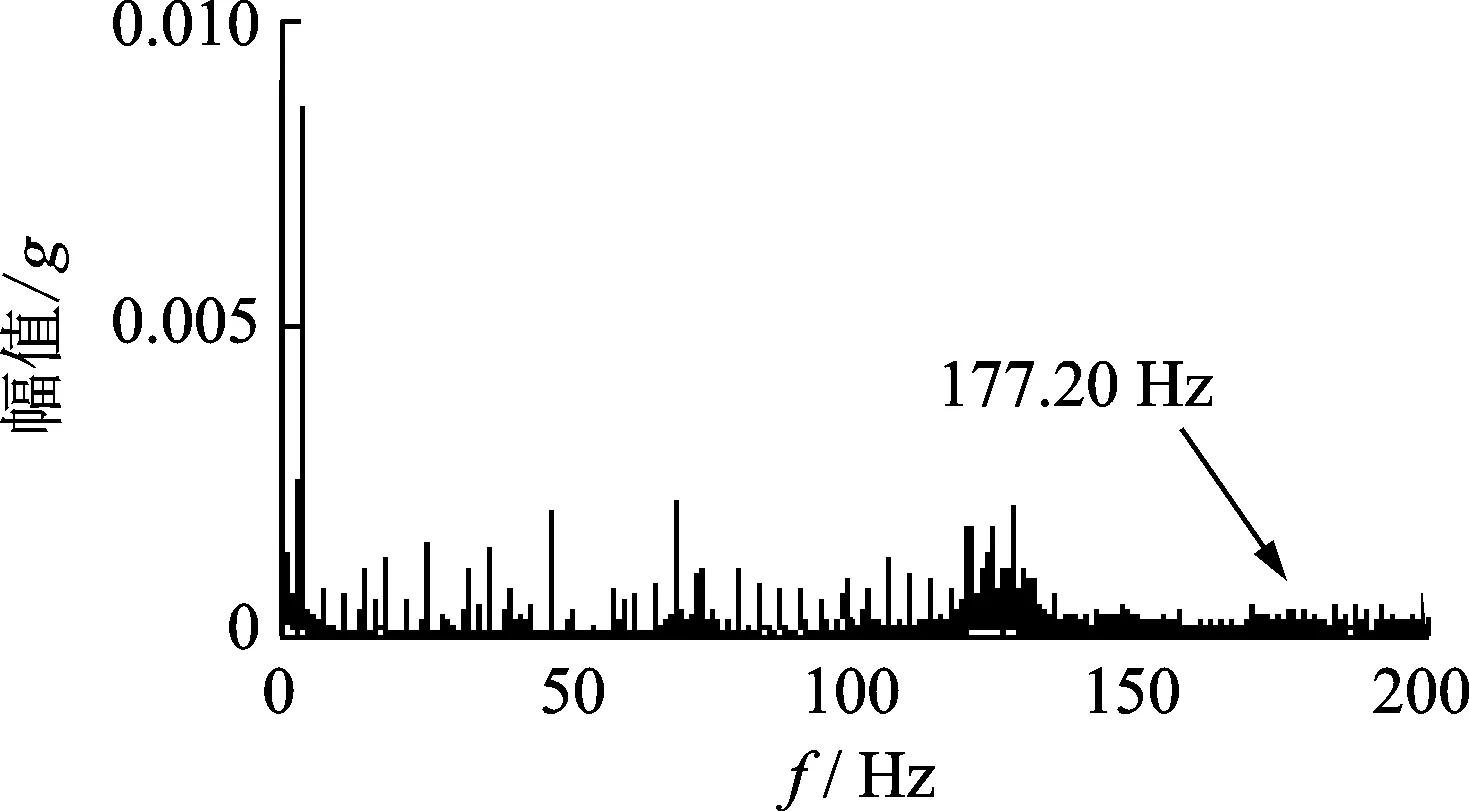
图2 内圈故障信号频谱Fig.2 The spectrum of inner race fault signals

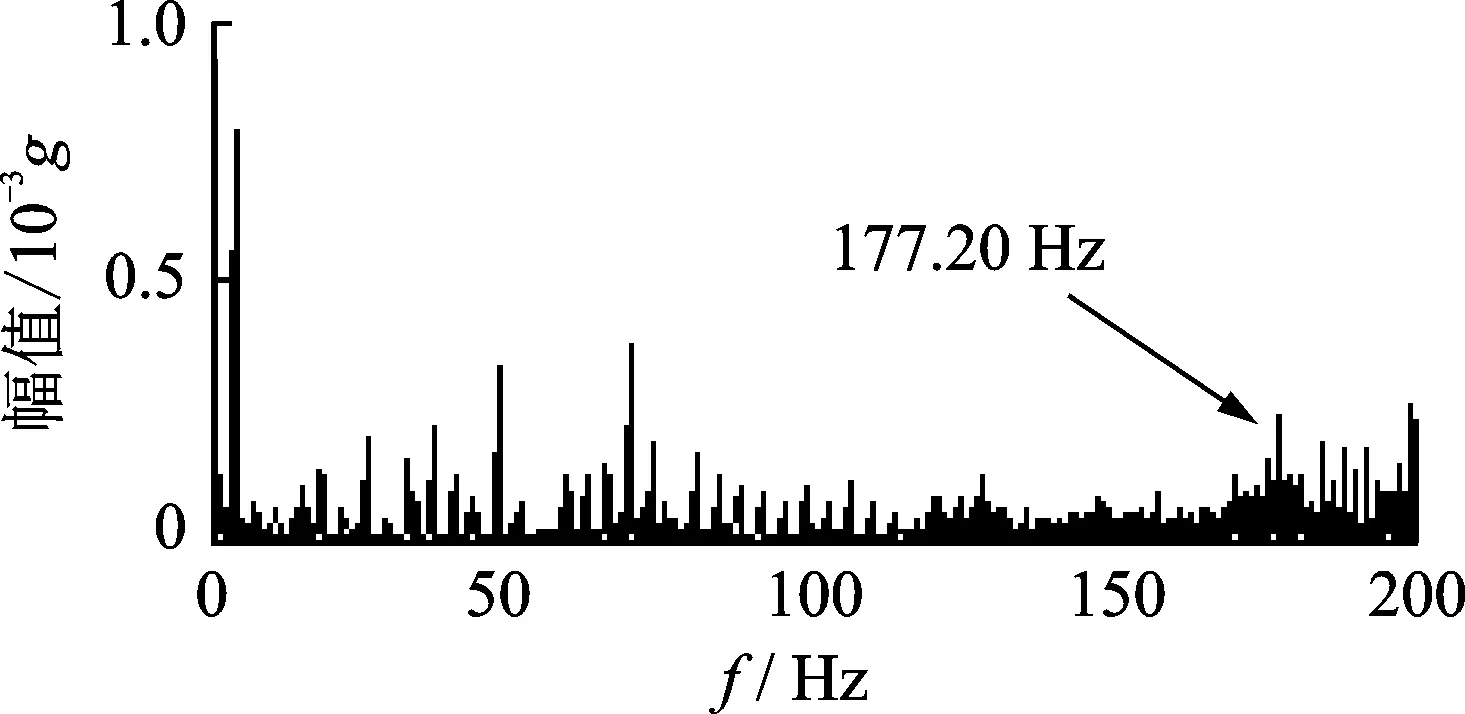
图3 内圈故障信号MED降噪后的频谱Fig.3 The spectrum of MED de-nosed inner race fault signals

再对MED降噪后的数据进行包络计算得到包络信号，为了观察效果，对包络信号进行频谱分析得到包络谱，如图4所示。与图3相比，图4中177.20 Hz处出现了清晰可见的边频带，而且噪声得到了很好的消除。

图4 内圈故障信号MED降噪后包络谱Fig.4 The envelope spectrum of MED de-nosed inner race fault signals

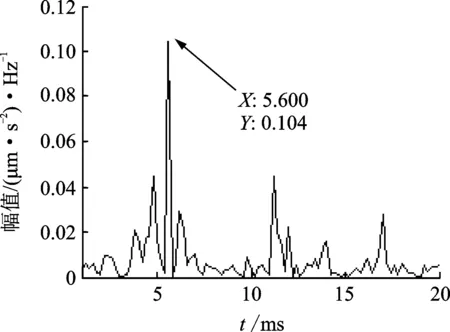
图5 内圈故障信号MED降噪后倒包络谱Fig.5 The envelope cepstrum of MED de-nosed inner race fault signals

为了进一步消除边频带的影响，对包络信号进行倒频谱分析，可以将包络谱图上的边频带简化为倒频谱上单根谱线,如图5所示。从图5上很容易发现,在5.6 ms处有非常明显的凸峰，对应内圈故障频率177.20 Hz的倒数，由此可以判断内圈出现了故障。

3.2 外圈故障

将外圈故障信号作频谱分析见图6所示，外圈故障频率169.55 Hz处的幅值完全被噪声掩盖，不能提取故障特征频率。采用本方法对外圈故障数据进行分析，首先采用MED方法对外故障信号进行预处理，结果为图7所示。与图6相比，图7中169.55 Hz处的幅值有所增强，但并不突出，而且仍然含有大量噪声。

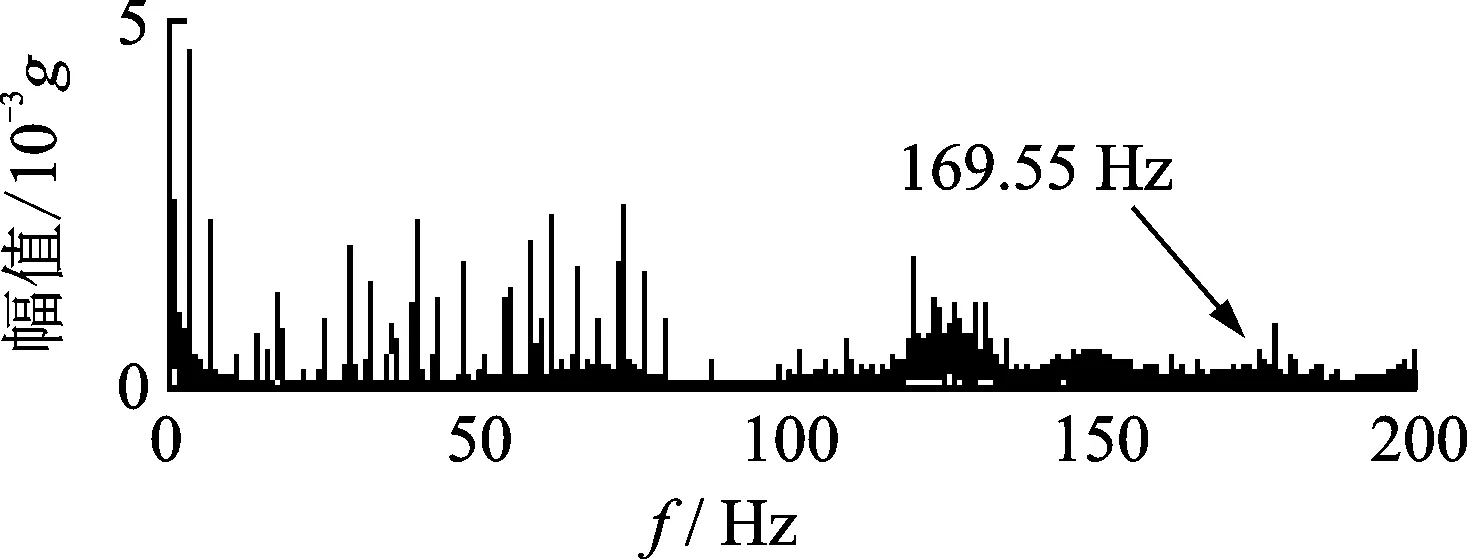
图6 外圈故障信号频谱Fig.6 The spectrum of outer race fault signals

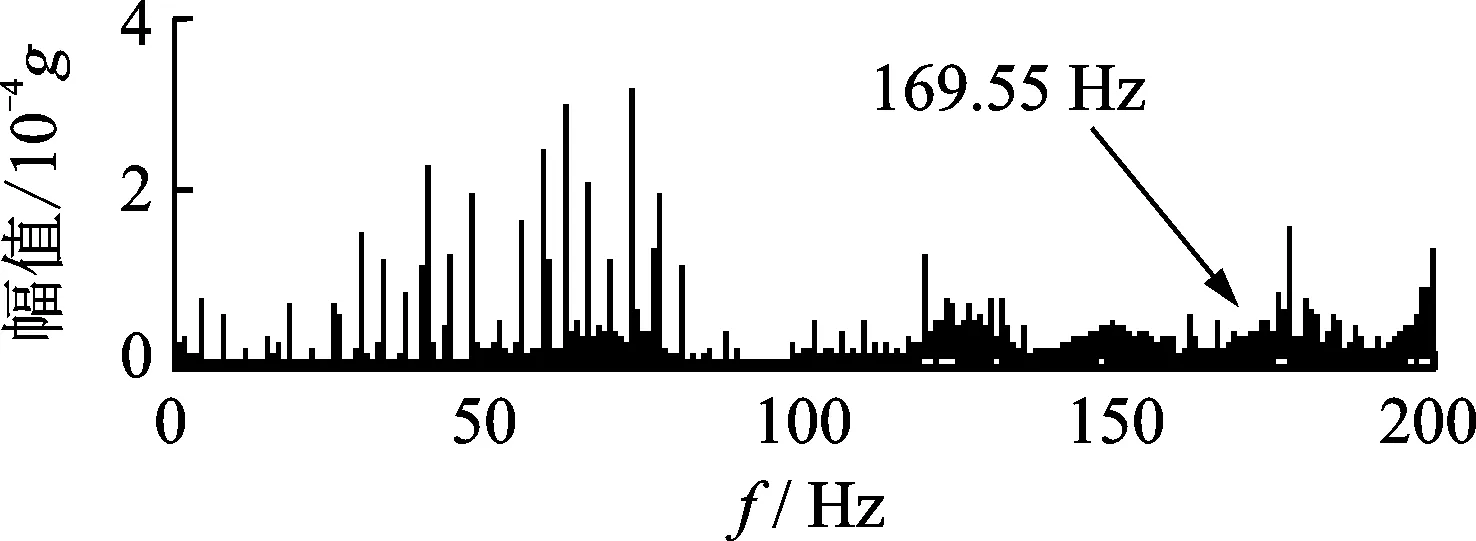
图7 外圈故障信号MED降噪后频谱Fig.7 The spectrum of MED de-nosed outer race fault signals

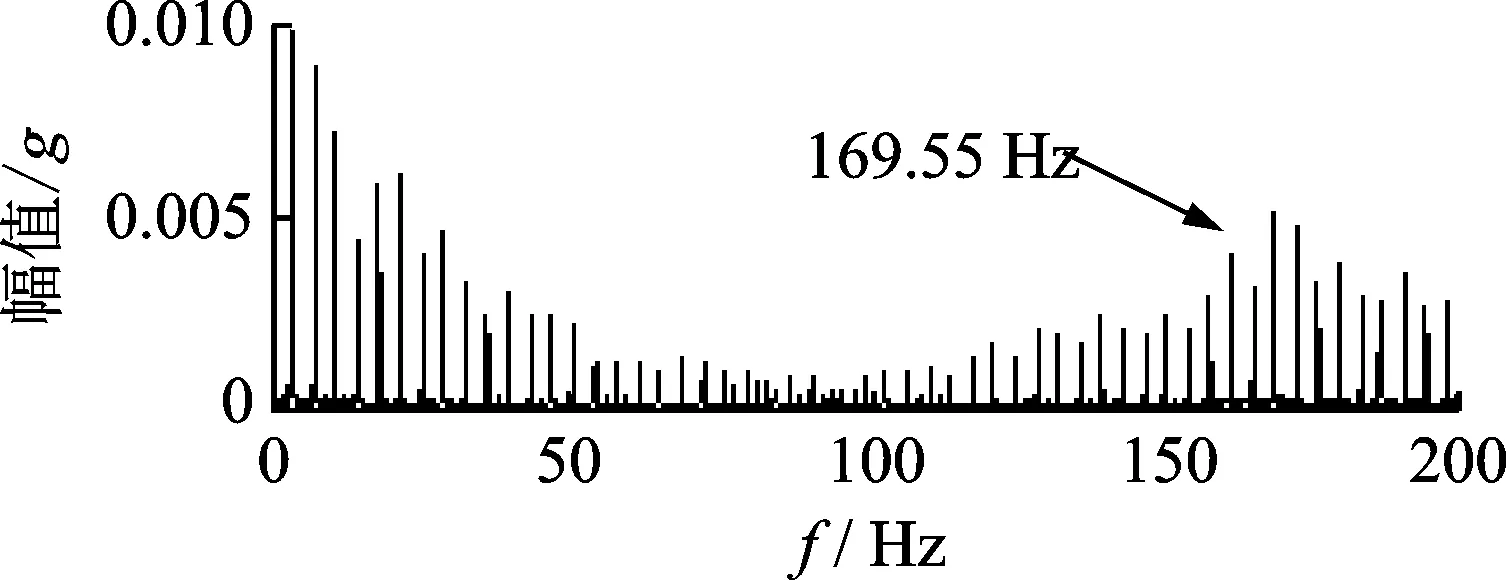
图8 外圈故障信号MED降噪后包络谱Fig.8 The envelope spectrum of MED de-nosed outer race fault signals

对图7中的数据进行包络计算，同样，对包络信号进行频谱分析得到包络谱如图8所示，与图7相比，图8上出现了清晰可见的边频带。

为了消除边频带的影响，对包络信号进行倒频谱分析如图9所示，从图9上很容易发现在6 ms处有较凸出的幅值，与外圈故障频率的169.55 Hz倒数相接近(采样率引起的误差)，同样此时可以判断外圈出现了故障。

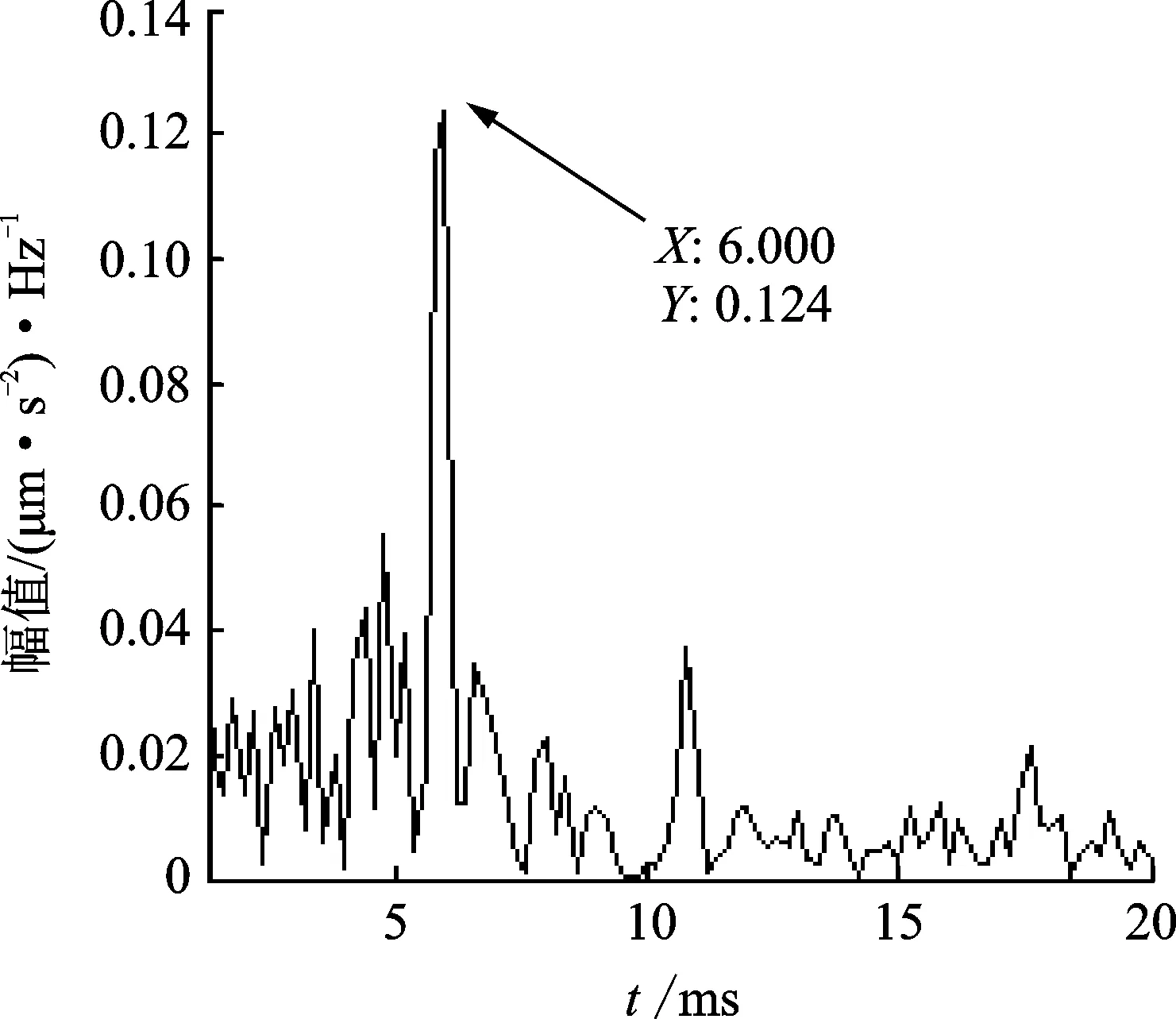
图9 外圈故障信号MED降噪后的倒包络谱Fig.9 The envelope cepstrum of MED de-nosed outer race fault signals

3.3 滚珠故障

将滚珠故障信号做频谱分析如图10所示，在滚珠故障频率71.69Hz处无明显幅值，无法提取故障特征频率。

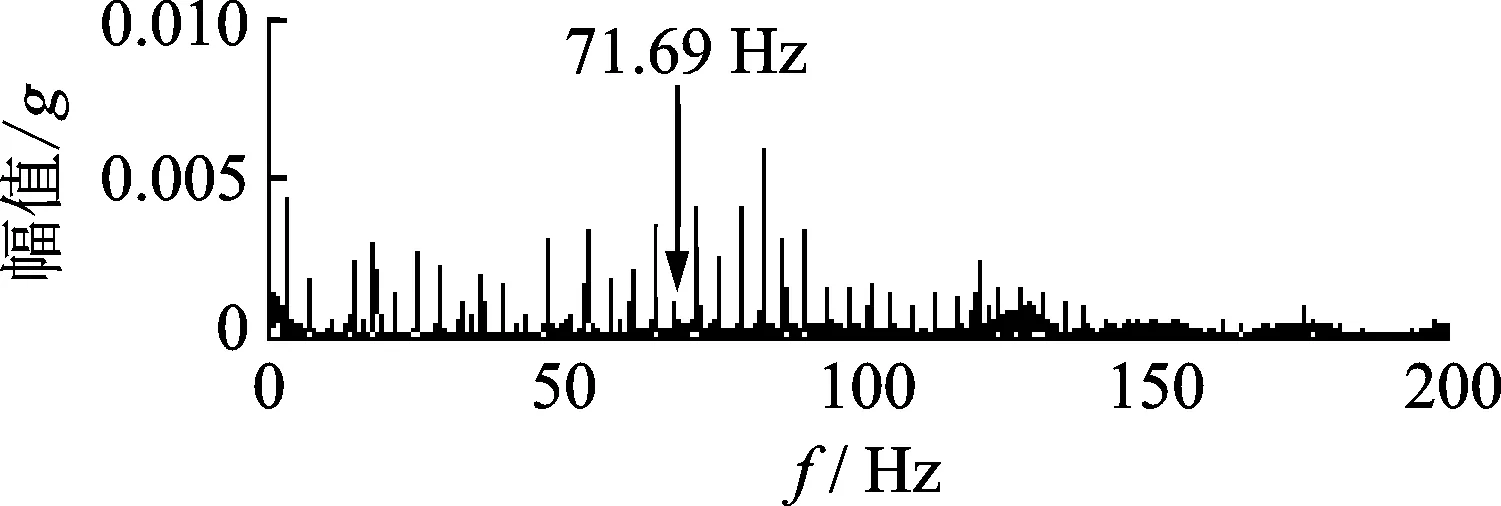
图10 滚珠故障故障信号频谱Fig.10 The Spectrum of ball fault signals

采用本方法对滚珠故障数据进行分析，首先采用 MED方法对滚珠故障信号进行预处理，结果如图11所示。

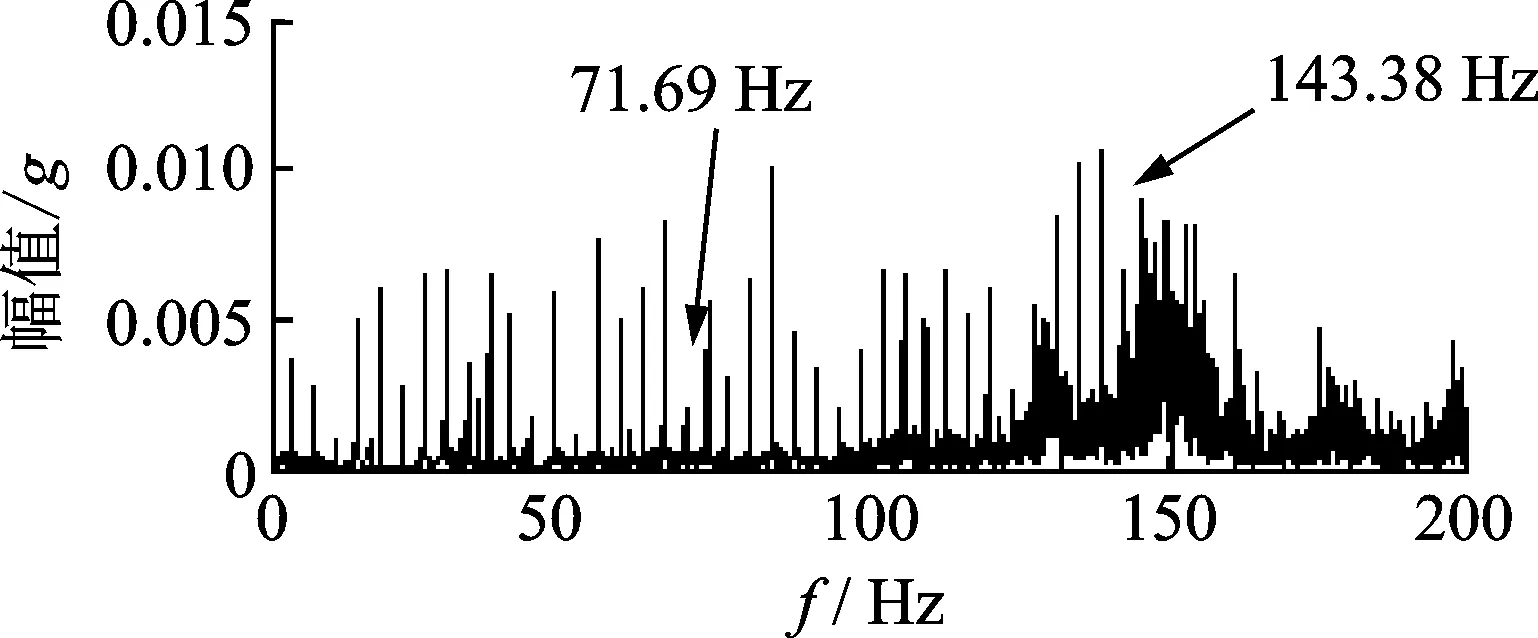
图11 滚珠故障信号MED降噪后频谱Fig.11 The spectrum of MED de-nosed ball fault signals

与图10相比，图11在滚珠故障频率和其2倍频附近的幅值得到了很大增强，但乃无法直接提取，仍然含有大量噪声；再对图11中的数据进行Hilbert包络计算，同样，对包络信号进行频谱分析得到包络谱如图12所示。

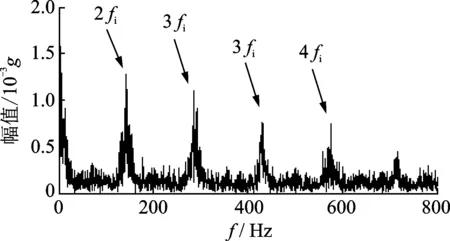
图12 滚珠故障信号MED降噪后包络谱Fig.12 The envelope spectrum of MED de-nosed ball fault signals

与图11相比，图12上在滚珠故障频率倍频附近出现了清晰可见的边频带，但是此时还无法定量分析。再对包络信号进行倒频谱分析如图13所示，从图13上可以看出，在7和14 ms处有明显的幅值，对应滚珠故障频率71.69 Hz和其两倍频143.38 Hz的倒数，由此可以判断滚珠出现了故障。

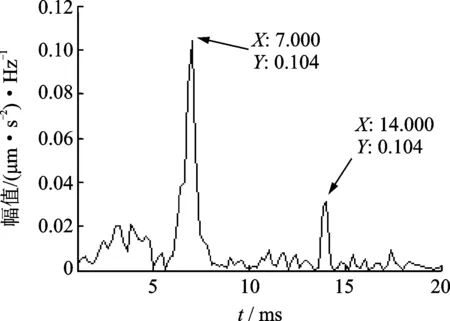
图13 滚珠故障信号倒包络谱Fig.13 The envelope cepstrum of ball fault signals

4 本方法与传统方法比较

采用传统的倒频谱方法分别对外圈、内圈和滚珠故障数据进行分析，结果如图14～16所示。虽然从传统的倒频谱上可以发现故障频率对应的位置，但是受到噪声的影响，幅值并不突出，而且周围的干扰谱线较多，诊断效果不理想。传统的倒频谱方法在提取滚动轴承早期故障特征时存在着明显不足。因此，本方法可以有效地去除噪声对倒频谱的影响，谱线更清晰，故障特征信息更突出，这为滚动轴承的故障诊断提供了一种新的方法。

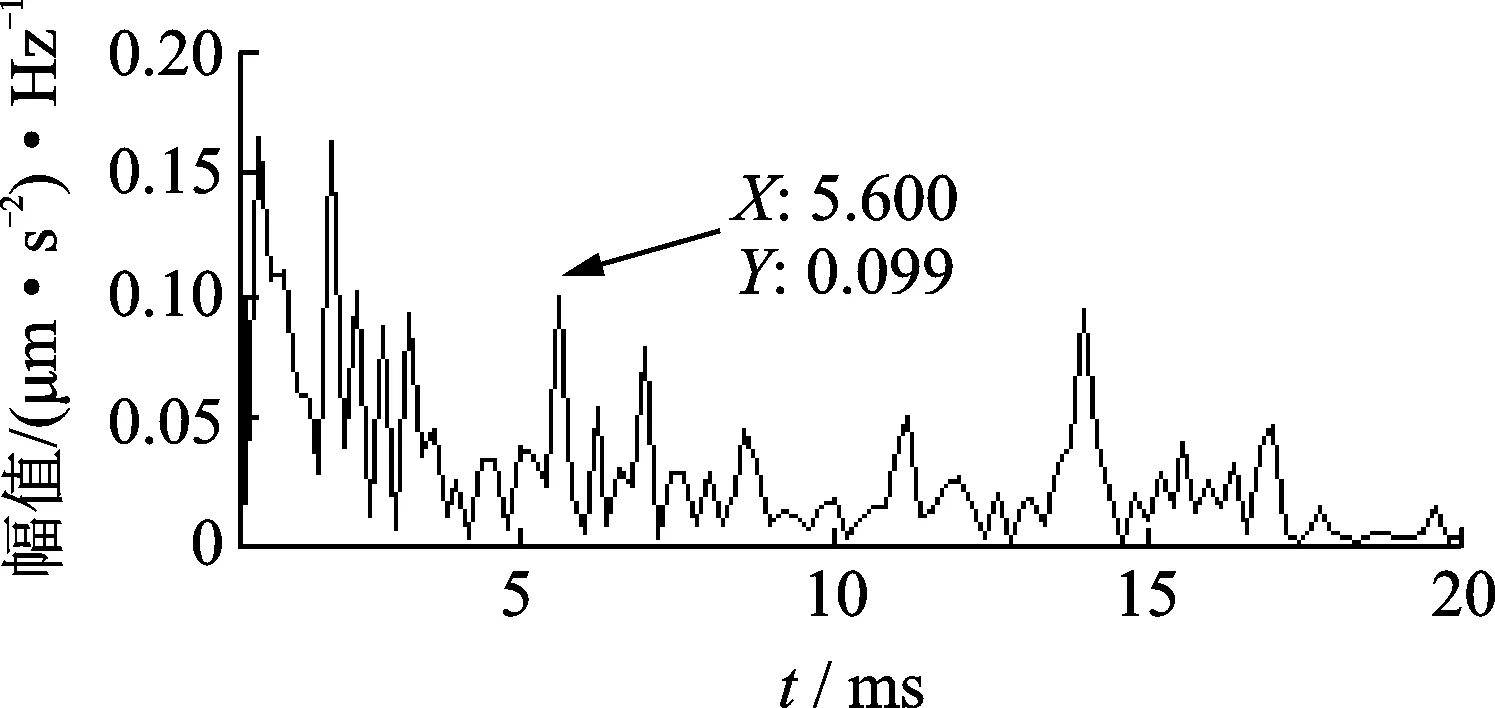
图14 内圈故障信号倒频谱Fig.14 The cepstrum of inner race fault signals

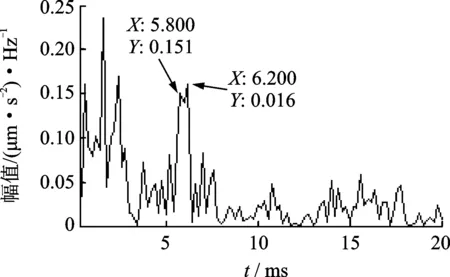
图15 外圈故障信号倒频谱Fig.15 The cepstrum of outer race fault signals

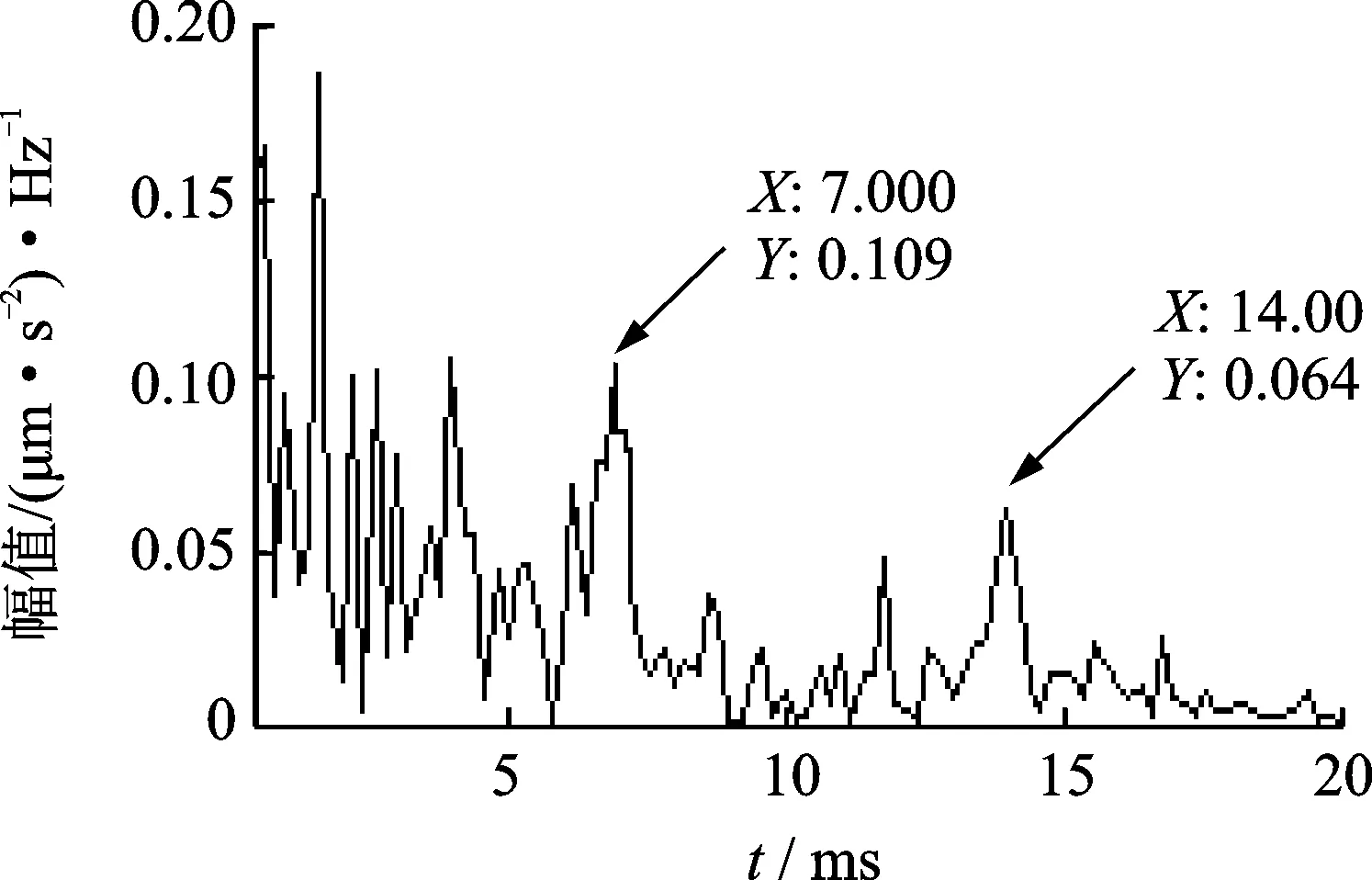
图16 滚珠故障信号倒频谱Fig.16 The cepstrum of ball fault signals

5 结束语

利用MED方法对信号进行降噪处理，同时增强信号中的冲击成分，再计算降噪后信号的包络，并对包络信号进行倒频谱分析，能够有效地提取滚动轴承外圈、内圈和滚珠故障特征频率。同时将本方法与传统的倒频谱分析方法进行对比，表明本方法能更有效地提取强噪声背景下的机械故障特征信息。