旋转机械转速波动检测及故障诊断*

谭 媛， 孙文磊， 温广瑞,， 黄 鑫

(1.新疆大学机械工程学院 乌鲁木齐，830047) (2.西安交通大学机械工程学院 西安，710049)

引 言

旋转机械是工业生产中最为常用的机械之一，广泛应用于电力、化工、冶金等行业，随着科学技术的进步与实际应用的需要，旋转机械向着高速化、大型化、自动化的方向发展，设备的尺寸越来越大，结构也越来越复杂，出现了大量的强度、结构、振动、可靠性等问题，旋转机械运行的环境也更加复杂，高温、高寒、交变载荷等恶劣环境导致机组的工况频繁发生变化，极易产生转速波动，此时机组产生的振动信号是典型的非平稳信号，直接进行傅里叶变换会产生频率混叠现象，无法区分转速波动过程各频振动分量。

Potter[1]提出阶比跟踪 (order tracking，简称OT)法，对振动信号进行角域重采样后再进行谱分析，消除转速波动引起的频率调制成分，构造角域阶次谱进行特征提取及故障诊断，有效避免了将非平稳信号直接进行傅里叶变换导致的频率模糊现象。

顾煜炯等[2]利用阶比重采样方法将时域信号转化为角域信号，使原始采集信号平稳化，利用无量纲指标分析早期故障趋势，基于多元统计分析建立故障预警模型，另外建立进行边界值检测的多元离群检测公式，后期应用主成分-灰色关联分析法精确故障。文献[3]采用经验模态分解方法得到包含故障信息的本征模态分量，对合成新信号进行阶次谱图以及倒阶次谱图分析，识别齿轮故障类型。姜战伟等[4]用参数优化变分模态分解将采集信号分解，然后通过重采样技术与Hilbert变换得到包络信号后，对包络谱进行阶比分析，得出故障特征。柏林等[5]将计算阶比跟踪方法与峭度图算法优势相结合，提出了阶比峭度图算法，并将其运用到滚动轴承故障特征提取中。程卫东等[6]通过对计算阶比跟踪技术与包络分析结合的集成故障诊断方法理论研究与实验验证，得出包络变形中相邻峰值间间距变化会对阶比分析产生影响，并提出消除影响的方法。王栋等[7]根据自适应拾取的不同频率分量的时频峰量，拟合实现瞬时频率估计，计算采样时标，进行重采样，并通过快速傅里叶变换实现阶比分析，提出旋转机械故障诊断新方法。以上方法舍弃了设备转速变化时的瞬态信息，具有一定的局限性。

杨扬等[8-9]提出了一种新的非平稳信号分析方法——参数化时频分析(parameterized time-frequency analysis，简称PTFA)，其本质思想是通过构造与信号匹配的变换核来对其进行时频域旋转，从而使信号时频表示的集中性达到最优。针对文中要解决的旋转机械运行转速波动导致状态信息获取及诊断决策困难问题，笔者在参数化时频分析理论基础上，引入单窗阶比理论及方法，进行旋转机械转速波动信息检测及故障诊断。

1 基于PTFA理论的短时阶比分析

1.1 PTFA基本原理

定义某信号s(t)∈L2(R)的解析信号为

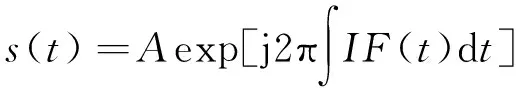
(1)

其中：瞬时频率IF(t)为时间t的函数。

为有效处理上述非平稳信号，假设任意函数kP(t)∈L2(R)，定义参数化时频分析如式(2)所示

(2)

其中

(3)

参数化时频分析的关键在于其变换核参数的估计，变换核参数与信号时频特征越匹配，其时频分辨率越高，对信号的时频特征表示越准确[8]，具体到转子振动信号处理，变换核参数的确定依赖于对转子瞬时转速(转频)的精确估计。

1.2 振动信号的瞬时频率估计方法

如何在无键相信号的情况下精确估计转子瞬时转速一直是一个热点和难点问题[10]，传统的基于STFT的瞬时频率估计方法假设待分析信号为拟平稳信号，在每个分析窗内具有平稳信号的统计特征，并不适用于转速波动剧烈的振动信号处理。

Iatsenko等[11]基于动态规划思想提出了快速路径优化算法(fast path optimization，简称FPO)，可以有效提高信号瞬时频率估计的精度和效率。

对于转子振动信号z(t)，其短时傅里叶变换(short time Fourier transform，简称STFT)为

(4)

Qm(t)=|STFTs(vm(t),t)| (m=1,2,…,Np(t))

(5)

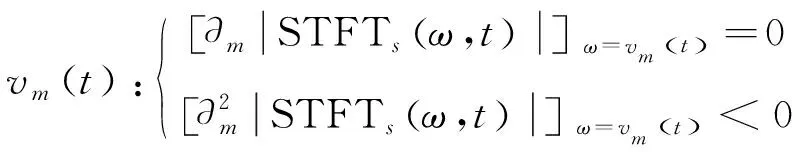
(6)

其中：Qm(t)，vm(t)分别为时频平面t时刻第m个局部极大值点的幅值和频率[12]。

实际运算中由于频率的离散性导致瞬时频率估计出现误差，为提高估计精度，需对局部极大值点的频率坐标进行插值校正[13]。

(7)

a{1,2,3}=|STFTs(ω{kp(t)-1,kp(t),kp(t)+1},t)|

(8)

其中：a1和a3为时频平面局部峰值a2相邻的两点。

瞬时频率变化曲线ωp(t)可通过追踪每一时刻局部极大值点的位置mc(t)进行估计

ωp(t)=vmc(t)(t)

(9)

通过构造代价函数

F[Qm(tn),vm(tn),vk(tn-1)]=

logQm(tn)+ω(vm(tn)-vk(tn-1))

(m=1,2,…,NP(tn))

(k=1,2,…,NP(tn-1))

(10)

可将式(9)转化为优化问题

(11)

1) 当n=1时

q(m,t1)=0

(12)

U(m,t1)=log(Qm(t1))

(13)

2) 当n≥2时

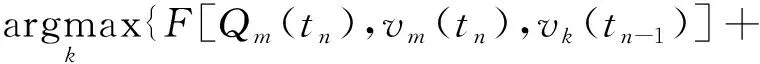
U(k,tn-1)}

(14)

U(m,tn)=F[Qm(tn),vm(tn),vq(m,tn)(tn-1)]+

U(q(m,tn),tn-1)

(15)

1.3 基于PTFA的短时阶比原理

对OPT算法求得的瞬时频率变化曲线ωp(t)进行高阶多项式拟合

(16)

其对应的倍频分量瞬时频率变换为

(17)

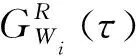
(18)

(19)

并进行参数化时频变换

(20)

其中

(21)

从而获得更加精确的时频域表示。

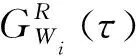
(22)

如图1所示,PTFA的变换结果等价于在Wi时窗内对信号进行角域重采样，在频域内表现为原来频率模糊的各分量频谱集中于一点mb1， 其实质上是对Wi时窗内的信号进行阶次分析，频率旋转后的频谱为对Wi时窗的各阶分量进行角域重采样之后的阶次谱，

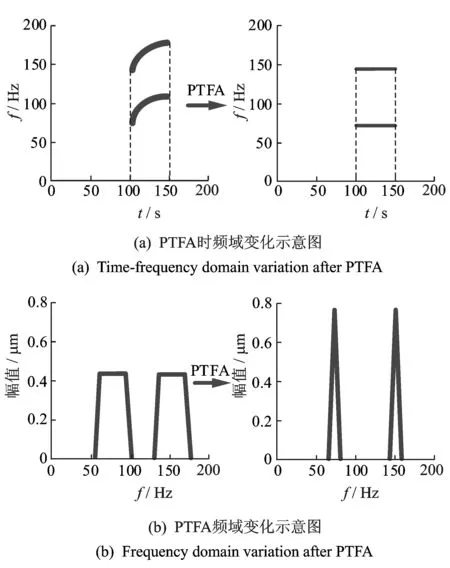
图1 参数化时频分析短时阶比示意图Fig.1 The short-time order tracking based on parameterized time-frequency analyze

将各时窗内的阶比谱按照时间轴排列可以得到振动信号的短时阶次谱，其保留了设备转速变化时的瞬态信息，可以更加清晰地了解机械设备的运行状态与故障信息。

2 仿真信号分析

2.1 仿真信号构造

为验证FPO方法检测转速波动的准确性，首先构造仿真信号进行分析。仿真信号采用Jeffcott模型，其数学表达式[14]为

y=Acos(ωt+α)

(23)

其中

(24)

(25)

其中：e为偏心距；ωn为转子固有频率；cn为阻尼系数。

按式(23)～(25)分别构造转频分量、倍频分量与分倍频分量，仿真信号转速波动规律为

ω(t)=100+20sin(t)

(26)

2.2 仿真信号分析

根据FPO方法与STFT峰值搜索方法分别进行仿真信号基频瞬时频率的估计，处理结果如图2所示；根据所估计的瞬时频率构造旋转算子和频移算子对仿真信号进行参数化时频变换，结果如图3所示。

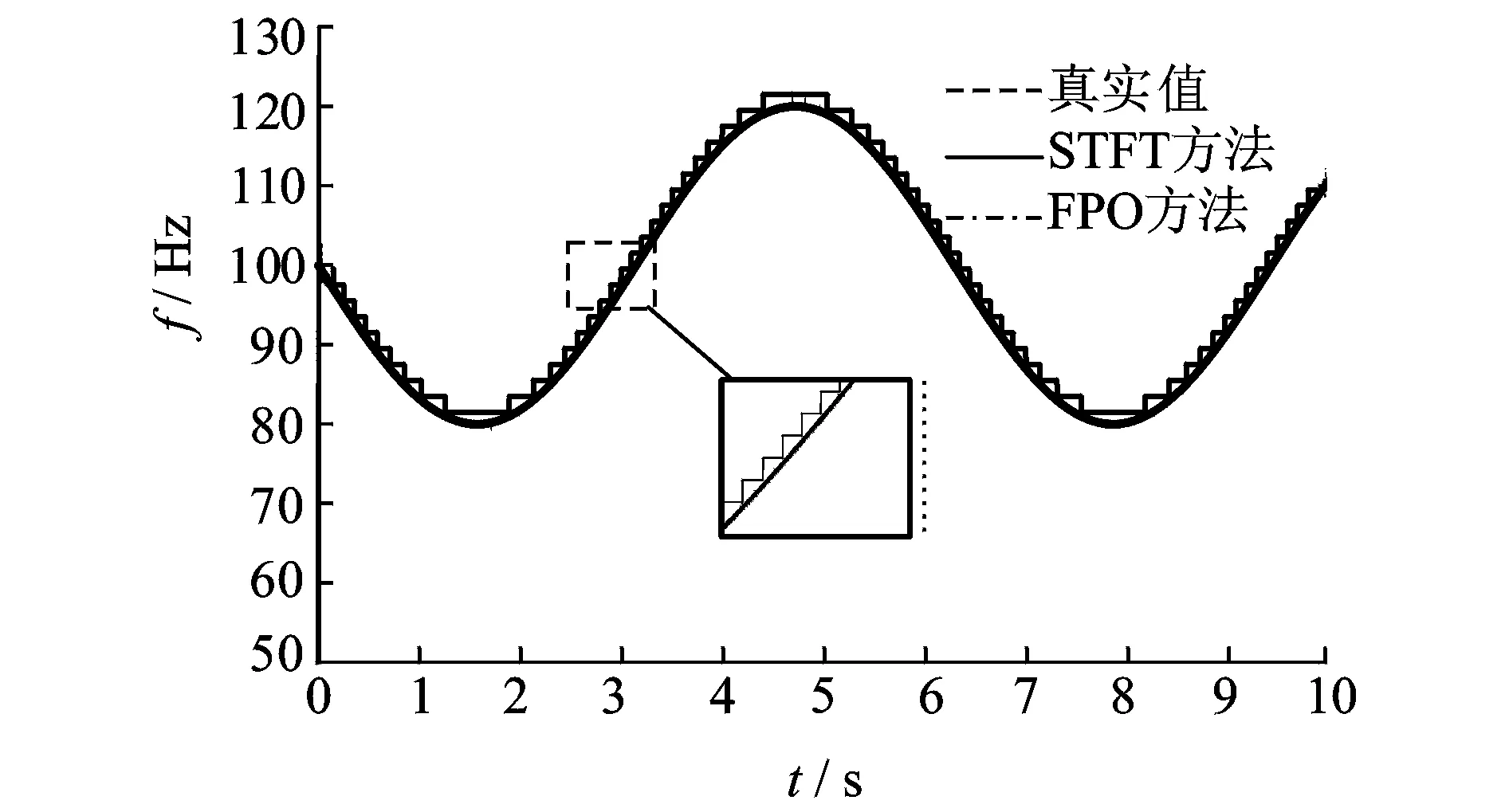
图2 仿真信号瞬时频率估计示意图Fig.2 Instantaneous frequency estimation of analog signal

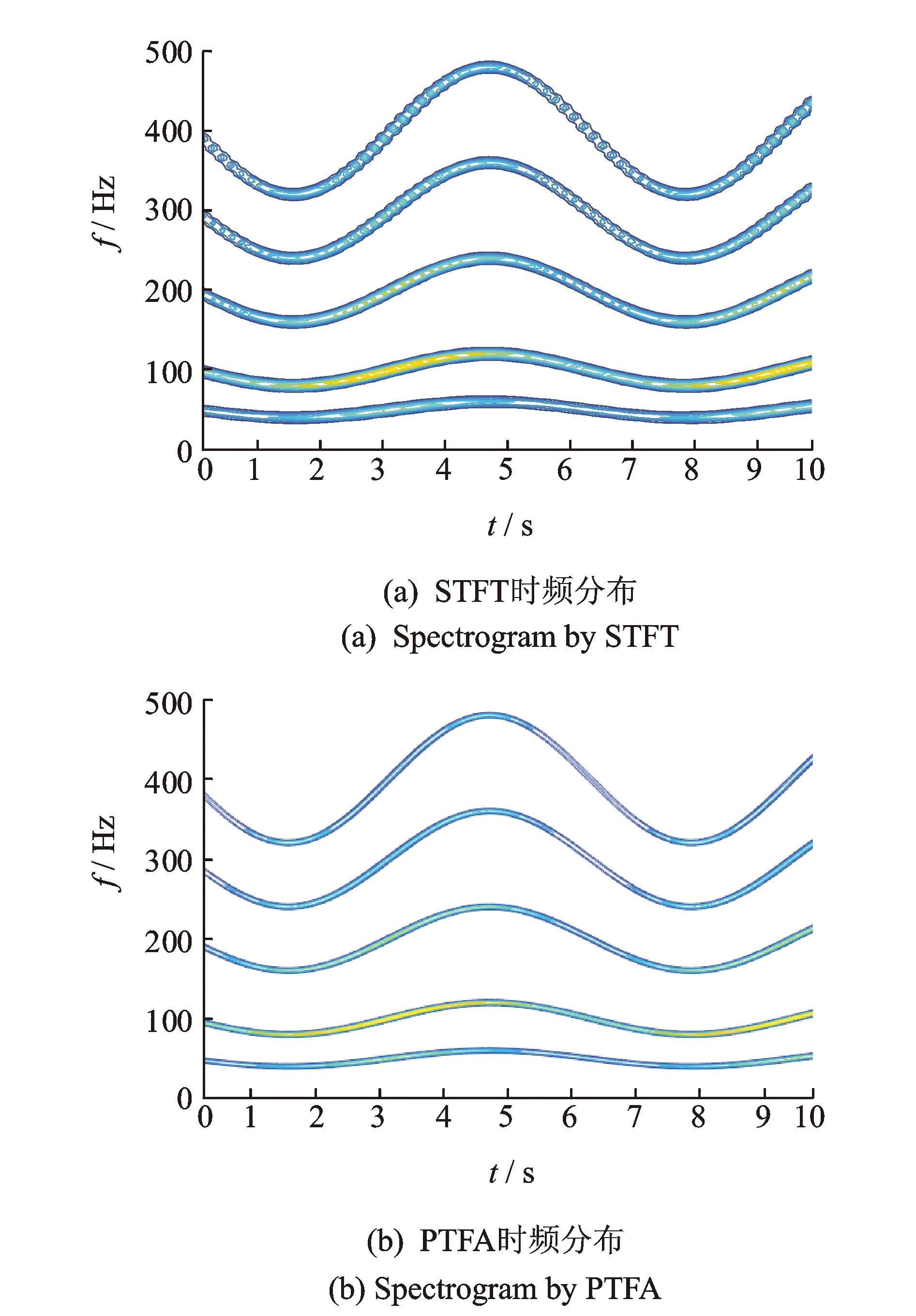
图3 仿真信号时频域谱图Fig.3 Time-frequency spectrogram of simulation signal

仿真结果表明该方法相比STFT而言具有更好的精度，定量分析两种方法估计的误差如表1所示。计算结果表明FPO瞬时频率估计方法能够有效地检测信号的瞬时波动，可以将其计算结果作为振动信号状态特征提取与故障诊断的依据。

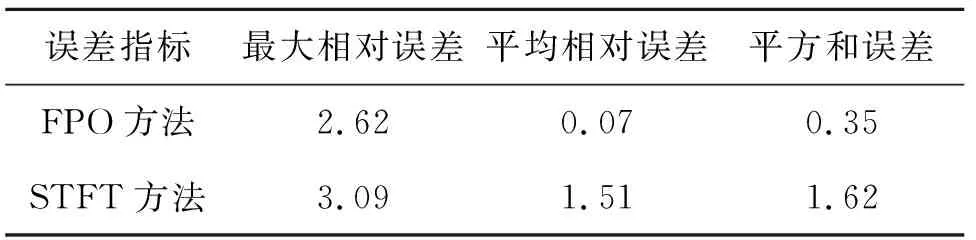
表1 仿真信号瞬时频率误差分析

3 实 验

在Bently RK4转子实验台上进行实验。为了充分考虑转子支撑各向异性的影响，分别在A，B两测量面上安装相互垂直的电涡流传感器，实验台结构和传感器安装如图4所示，K为键相传感器。

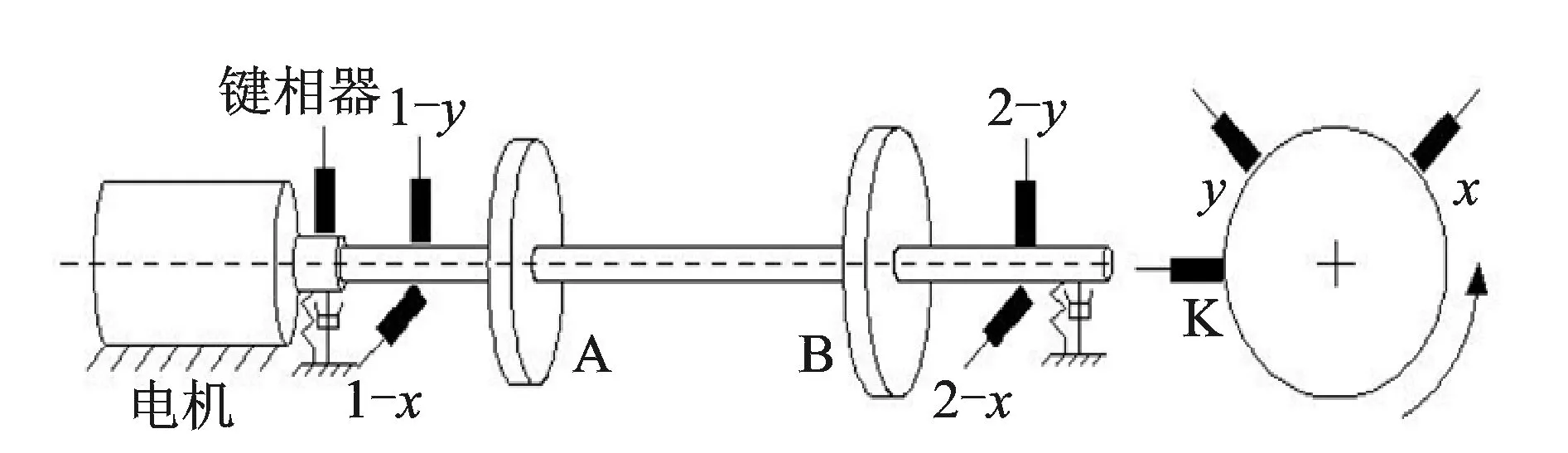
图4 传感器安装示意图Fig.4 The arrangement of sensors

3.1 转速波动检测实验

在Bently RK4实验台上采集真实转速波动信号进行验证，信号时域如图5所示。

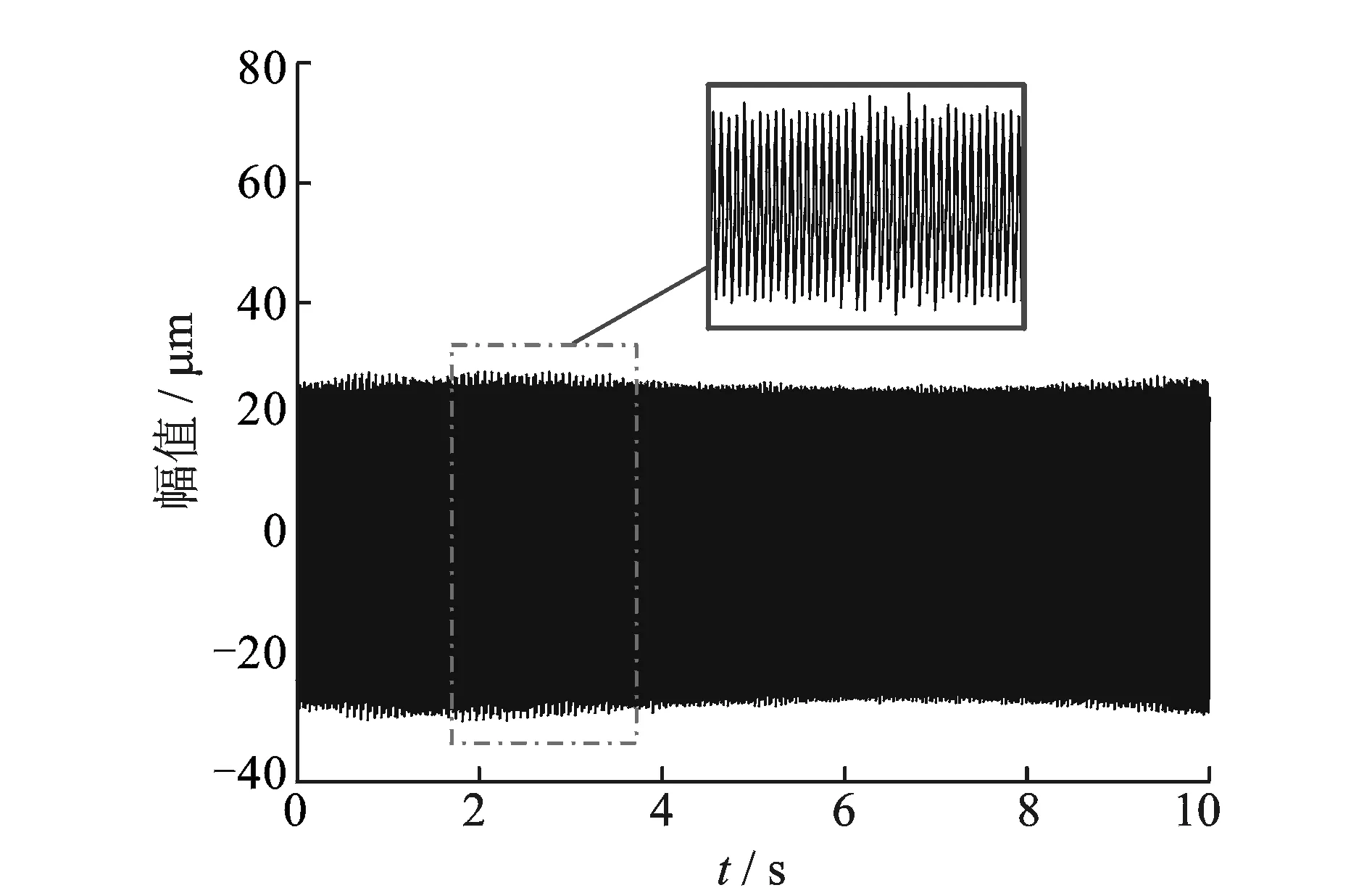
图5 转速波动信号时域波形Fig.5 Time domain waveform under speed fluctuations

根据FPO方法对实测信号进行转速波动检测，其结果如图6所示，处理结果表明振动信号转速波动变化剧烈时，STFT估计瞬时转速存在明显的阶梯效应，不适用于转速波动的检测与处理。根据所估计瞬时频率进行参数化时频分析，结果如图7所示，FPO-PTFA较传统的STFT具有更高的时频分辨率，可有效处理转速波动信号。

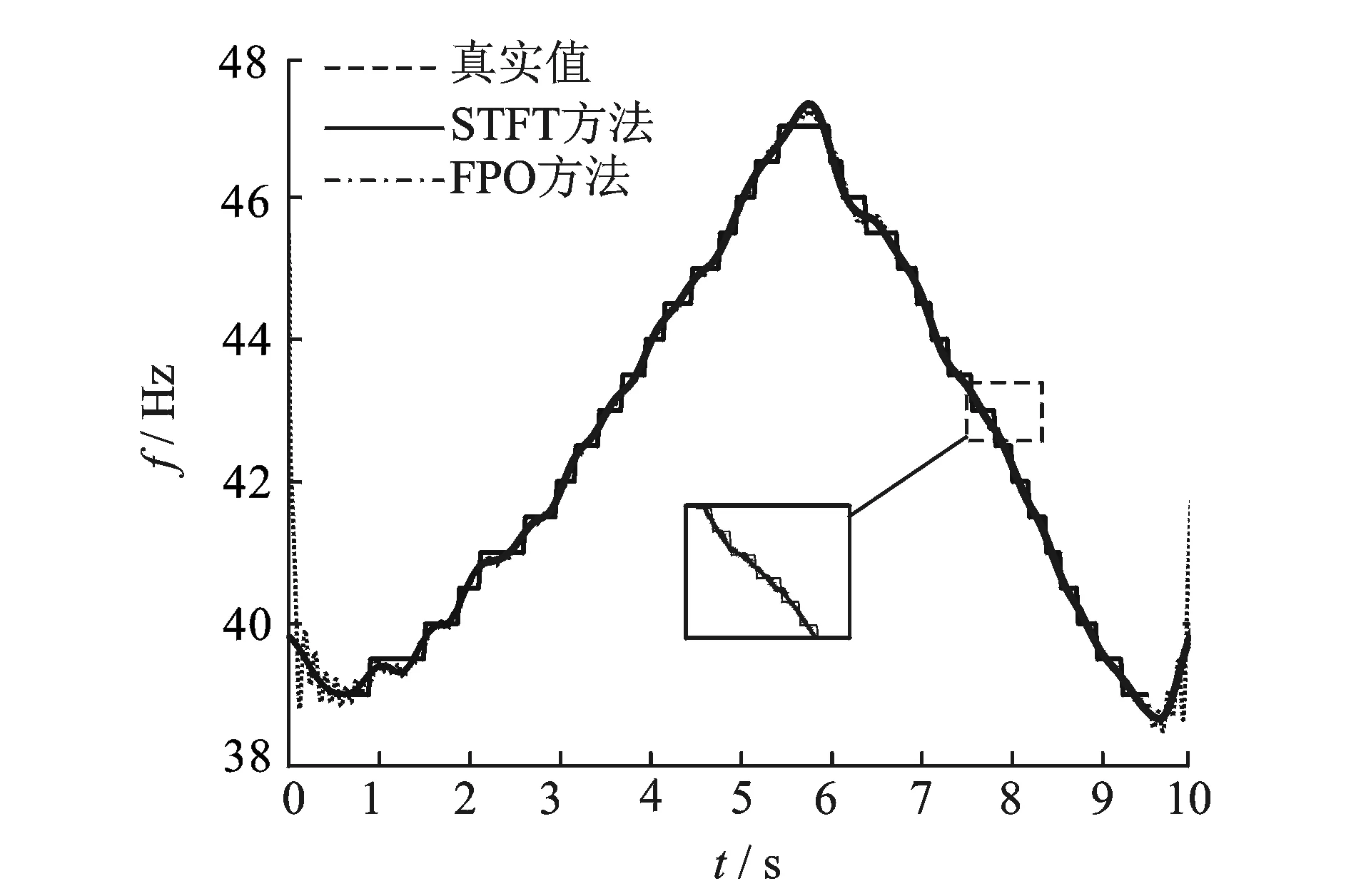
图6 实测信号瞬时频率估计示意图Fig.6 Instantaneous frequency estimation of measurement signal

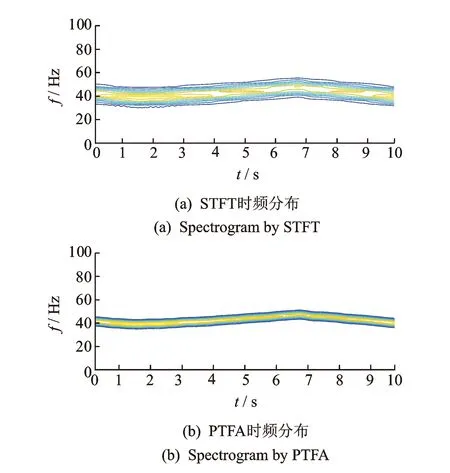
图7 实测信号时频域谱图Fig.7 Time-frequency spectrogram of measurement signal

表2分别给出了两种方法瞬时频率估计误差的定量评价结果，显然，FPO频率估计方法得到的结果相比于传统的STFT方法而言具有更高的精度。

表2实测信号瞬时频率误差分析

Tab.2Erroranalysisofmeasurementsignalinstantaneousfrequencyestimation%

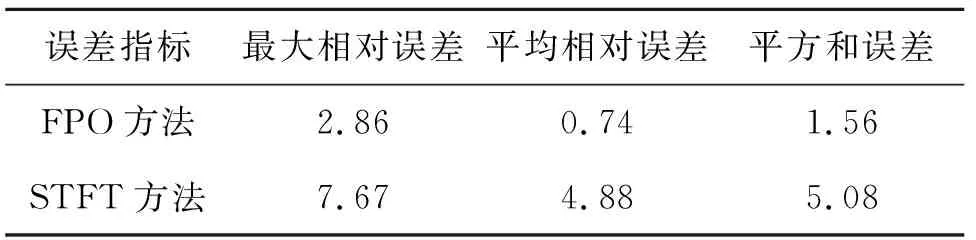
误差指标最大相对误差平均相对误差平方和误差FPO方法2.860.741.56STFT方法7.674.885.08

3.2 故障识别

分别采集正常，不平衡，不对中三种故障的转速波动工况下的振动信号，根据所估计的瞬时频率首先构造频率旋转算子进行时频域旋转变换求得振动信号的短时阶次谱，如图8～10所示。

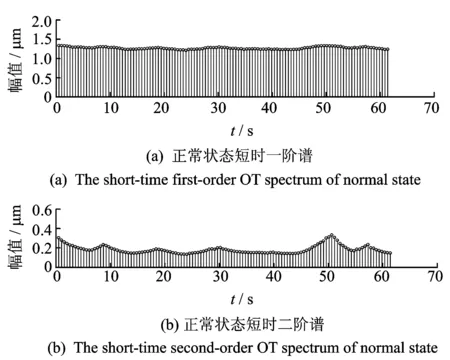
图8 正常状态转速波动阶次谱Fig.8 The short-time OT spectrum of normal state

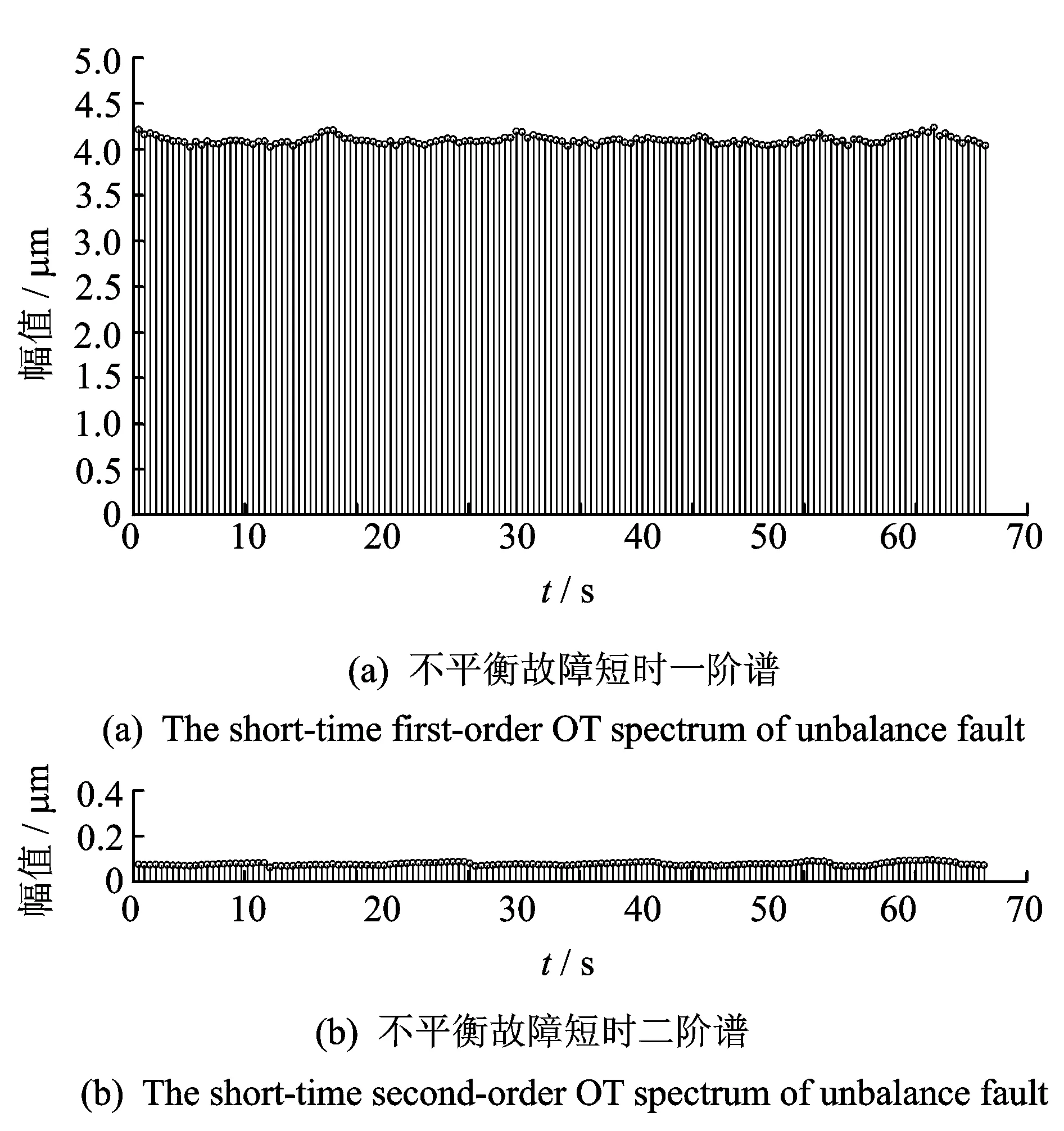
图9 不平衡故障转速波动阶次谱Fig.9 The short-time OT spectrum of unbalance fault

由转子三种状态的短时阶次谱可得，不平衡故障时的短时一阶谱较大，不对中故障时存在明显的二倍频分量，进一步观察发现，不对中故障时其短时二阶谱存在明显的波动现象，图10(b) 所示为短时二阶谱波动与转速波动对应关系，在3 500 r/min时，其二倍频阶次谱最大，在其他转速处较小。

为了进一步研究不对中故障二倍频阶次谱与转速的关系，分别采集不对中故障3 000～4 500 r/min的启车数据与停车数据，并比较启停车状态下转速与二倍频阶次谱对应关系，如图11所示，启停车振动信号短时二阶谱在3 500 r/min转速时达到峰值。

转子不对中主要影响振动信号的偶次倍频，当转子的转速远离其一阶临界转速的整数分频时，系统振动信号中以旋转引起的同步强迫振动为主，含有较少的偶次倍频分量；当转子的转速接近或等于其一阶临界的整数分频时，会引发偶次倍频的共振，振动信号中含有较多的偶次倍频分量，大型旋转机械一般工作在非亚临界转速下，不会激发出转子系统的偶次倍频，因此某个固定转速下以二倍频分量作为不对中故障的特征有可能发生误诊、漏诊。充分利用旋转机械转速波动的信息可以丰富故障诊断的手段，提高故障诊断的准确性。

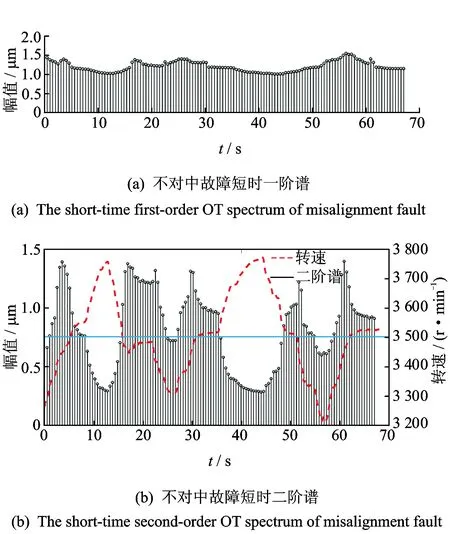
图10 不对中故障转速波动阶次谱Fig.10 The short-time OT spectrum of misalignment fault

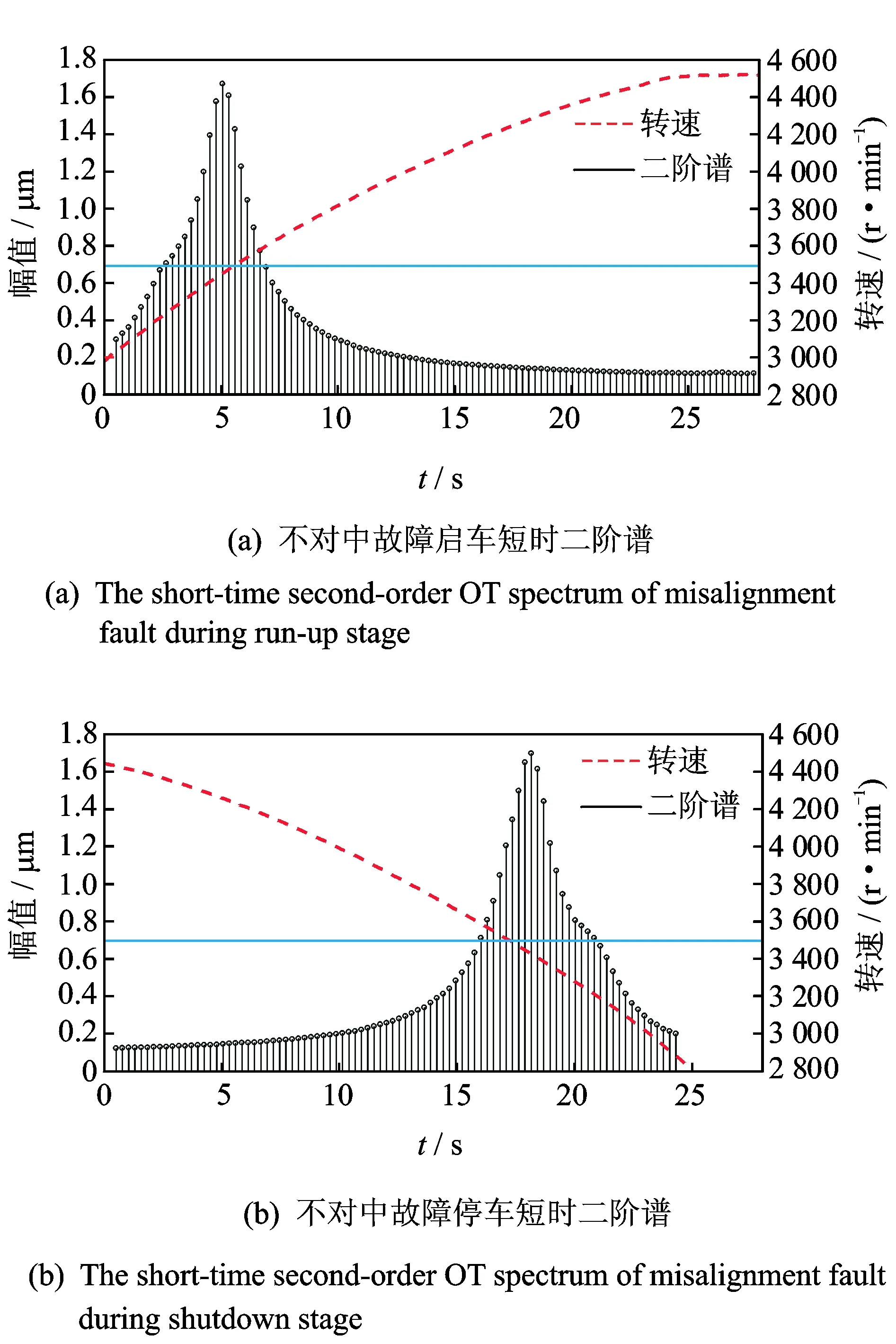
图11 不对中故障启停车阶次谱Fig.11 The order spectrum of misalignment fault during run-up and shutdown stages

4 结束语

采用快速路径优化算法进行旋转机械转速波动的检测，并进行了仿真信号分析和实验验证。结果证明，该检测方法较传统方法更为精确，为后续的故障特征提取提供更为可靠地依据。基于参数化时频分析理论提出了短时阶比分析方法，并应用于转子不平衡与不对中故障的诊断，阐述了转速波动工况下不对中故障的二阶谱波动现象并分析了产生波动的原因。实验结果表明，应充分利用旋转机械转速波动的瞬态信息进行机械运行状态监测与故障诊断。