直升机尾传轴系相对位置变化下啮合力分析*

蒋玲莉， 印道轩， 李学军， 冯和英

(湖南科技大学机械设备健康维护省重点实验室 湘潭，411201)

1 问题的引出

直升机传动系统包括主减速器、中间减速器、尾减速器、主旋翼轴、动力传动轴和尾传动轴，即“三轴三器”，具有结构紧凑、重量轻、工艺精度高、传动功率大和减速比高等特点，将发动机的动力传递给旋翼和尾桨，是直升机不可缺少的关键核心部件，典型结构如图1所示。

图1 典型直升机传动系统结构示意图Fig. 1 Schematic diagram of typical helicopter transmission system

直升机的飞行环境恶劣，所受的载荷复杂多变，减速器、轴系及旋翼之间相互耦合的扭振及横振大，“三轴三器”在主旋翼和尾桨的载荷作用下容易产生轴系相对位置的变化。如此复杂的轴系结构，任何轻微的轴系相对位置变化都将导致整个传动系统传递特性变化，进而引起支撑轴承过早地损坏，缩短轴承的使用寿命；造成齿轮啮合处产生较大的冲击和齿面的摩擦，从而产生振动冲击，影响传动系统的性能,使传动系统受到额外的激励力从而显著降低传动系统的工作寿命等。研究直升机轴系相对位置变化下的动力学响应特性，揭示其典型工况下运行机理，为直升机传动系统运行状态监测提供理论依据。

文中以直升机尾传系统——输入输出轴相互垂直的一对螺旋锥齿轮结构为研究对象，研究其轴系相对位置变化下的啮合力变化规律。尾传系统在尾桨的载荷作用下，会使尾桨轴产生轴拉力，从而导致轴上下移动，造成了尾桨轴的偏移位置L的变化，如图2(a)所示。在桨叶的载荷作用下，会使尾桨产生附加弯矩，从而使尾桨轴发生倾斜，造成尾桨轴的倾斜位置β的变化，如图2(b)所示。

图2 尾传轴系相对位置变化示意图Fig. 2 Relative position change of diagram tail shaft

国内外学者对齿轮系统动力学特性的研究做了大量的工作。王奇斌等[1]研究了齿轮啮合时，齿距偏差对齿轮啮合特性的影响。Zhan等[2]研究了一种基于ANSYS软件中的Workbench模块和准静态算法来确定齿轮时变啮合刚度的新技术，并考虑了齿轮副不对中对啮合刚度的影响。Luo等[3]研究了齿轮中心距离的变化对齿轮时变啮合刚度的影响。张慧博等[4]分析了径向误差与齿侧间隙的耦合故障对齿轮系统动力学特性的影响。任菲等[5]分析了各构件制造偏心误差和齿廓误差以及陀螺效应等激励因素对行星轮的均载特性的影响。刘延伟等[6]考虑了时变啮合刚度、齿侧间隙和接合间隙等激励建立了齿轮传动系统动力学模型，研究了齿侧间隙对齿轮系统非线性特性的影响。程哲等[7-8]对齿轮的断齿、点蚀等故障下的齿轮-转子系统动力学特性进行了研究。以上文献主要从时变啮合刚度、齿侧间隙、传递误差和齿轮的局部故障来研究齿轮系统动力学响应特性。笔者主要从齿轮轴系相对位置变化的角度来研究齿轮系统的动力学响应特性，是对直升机传动系统动力学及齿轮系统动力学的补充和完善。

2 尾传轴系相对位置变化动力学模型

首先，根据齿轮系统动力学中的齿轮啮合原理建立螺旋锥齿轮的动力学模型；然后，计算轴系位置变化下的时变啮合刚度和时变啮合阻尼，将其代入正常状态下的动力学模型中，得到轴系位置变化下的动力学模型。

2.1 螺旋锥齿轮动力学模型

对于弧齿锥齿轮传动，其啮合点半径与啮合位置有关，在实际分析中，取啮合点半径为齿宽中点处的回转半径，且两齿轮的螺旋角为0，可将其视为直齿锥齿轮[9-10]。图3为齿轮动力学示意图。

图3 齿轮啮合动力学模型Fig.3 Gear meshing dynamic model

图3中:T1，T2，R1，R2，ω1，ω2分别为两轮的转矩，基圆半径和转速；c，k分别为啮合阻尼和啮合刚度。

仅考虑扭转振动，系统的自由度分别为两齿轮的扭转角θ1，θ2，根据简化的扭转振动简图可得到其分析模型[11-12]为

(1)

(2)

x(t)=r1θ1-r2θ2-e(t)

(3)

将时变啮合刚度k(t)，以及啮合阻尼c代入式(1～3)中，可得到齿轮啮合等效动力学模型

(4)

W=T1/r1=T2/r2

(5)

其中：me为等效质量；W为等效载荷。

2.2 尾传轴系相对位置变化的动力学模型

假设尾传动系统在尾桨载荷的作用下，尾桨轴发生偏移位置变化或倾斜位置变化，尾传输入轴不变，其轴系相对位置变化等效图如图4所示。

图4 尾传轴系相对位置变化等效图Fig.4 Equivalent graph of relative position change of tail shaft

图4中AB为分度圆处的啮合线，L为偏移量，β为倾斜量。若竖直轴向上平移L，则在分度圆处啮合线AB的垂直方向上平移Δα1；若竖直轴向右倾斜一个β角度，则在分度圆处啮合线AB的垂直方向上平移Δα2的等效长度。

如图5所示，Pb1，Pb2分别为两齿轮的啮合线，由于齿轮轴的位置偏移会导致两齿轮出现齿侧间隙，齿侧间隙j与位置偏移量Δa的关系[13-15]为

2(r+Δa)(inv(αa)-inv(α))

(6)

(7)

inv(αi)=tanαi-αi

(8)

其中：m为齿轮模数；r为分度圆半径；rb为基圆半径；α为分度圆压力角；αi为任意圆压力角。

图5 齿侧间隙 Fig. 5 Backlash

由于轴系相对位置变化导致了齿侧间隙的存在。根据尾传齿轮对的等效直齿轮对的重合度为1.6，再结合图5可知，由于齿侧间隙的存在会使得第一对齿轮离开以后到第二对开始啮合的时间增加，即增加了单齿啮合的时间。将轴系偏移位置变化当成中心距Δa的变化，即悬臂梁的臂长增加，形成了固定的齿侧间隙；轴系倾斜位置变化造成齿轮副沿齿宽方向出现均匀变化的齿侧间隙，因此轴系倾斜位置变化的啮合刚度除了脱齿区域以外还会有一个过渡区。根据以上刚度变化理论分析再结合文献[7，8]中的故障齿轮啮合刚度综合计算方法，得

k=F/(δa1+δa2+δh)

(9)

其中：k为齿轮啮合刚度；F为某一位置处的啮合力；δa1,δa2分别为两齿轮齿廓某一位置处的弯曲变形；δh为接触变形。

首先，根据截面悬臂梁的假设，齿轮弯曲变形δa可采用Weber公式计算，即

(10)

其中：F为啮合力；αm为压力角；G为剪切模量；sh为剪切因子；xi和di的物理意义如图6所示。

(11)

其中：Ji为Si的极惯性矩；Ai为Si的面积。

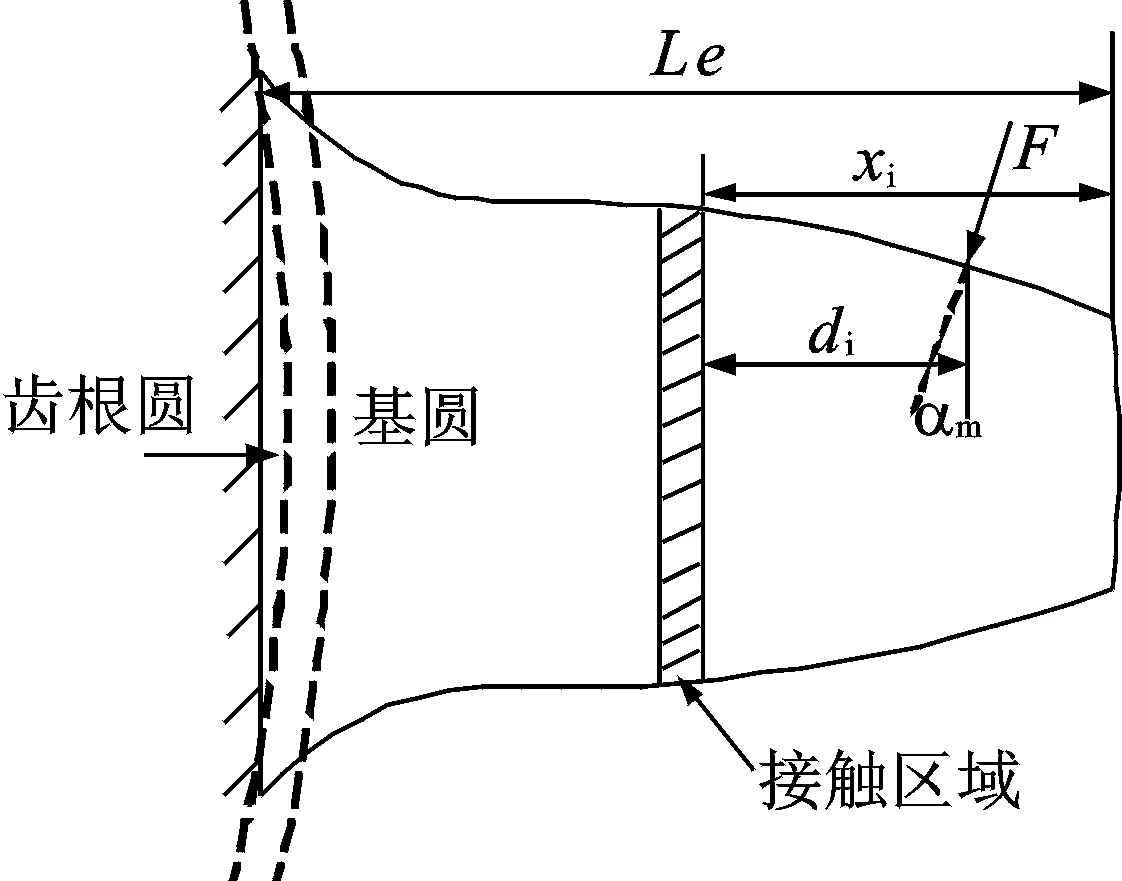
图6 齿轮弯曲变形计算模型Fig. 6 Calculation model of gear bending deformation

图6中：Le为齿的全长；xi为接触区域到齿顶的距离；di为接触区域到啮合力作用点的距离；αm为啮合力与竖直轴的夹角。

然后，根据Hertzian接触理论计算接触变形δh

(12)

其中：ν为泊松比；E为弹性模量；B为齿宽。

根据上述计算公式将齿廓分为有效个点，分别计算得到不同轴系偏移量和倾斜量下的齿轮弯曲变形和接触变形，然后算出各点的刚度，并拟合成线。图7分别为偏移量为0.3 mm和倾斜量为0.3°时的时变啮合刚度曲线。

图7 轴系相对位置变化下时变啮合刚度Fig.7 The time-varying meshing stiffness under the change of relative position of shafting

最后，将周期变化的啮合刚度用傅里叶级数进行5阶展开，得到时变啮合刚度曲线公式如下

(13)

其中：km为齿轮副的平均啮合刚度；k1n和k2n为谐波项啮合刚度的幅值；nω为齿轮啮合频率。

轴系相对位置变化下啮合阻尼cm可由下式计算求解

(14)

(15)

其中：ξ为阻尼比，一般在 0.03～0.17 范围内，根据经验一般取阻尼比ξ=0.06。

将所求出的齿轮轴系相对位置变化下的时变刚度k1(t)和啮合阻尼cm带入正常的齿轮啮合动力学模型式(4)中，即可得到尾传轴系相对位置变化下的动力学模型。

(16)

3 直升机尾传轴系相对位置变化响应特性分析

以尾传轴系相对位置变化的动力学模型为依据，结合多体动力学软件ADAMS展开后续分析。已知某型直升机尾传系统的齿轮结构参数：弹性模量为2.07×105MPa；两齿轮的齿数分别为23和64，模数为6 mm，螺旋角为0°，压力角为22.5°，齿宽为50 mm。

根据以上的齿轮参数，以该型直升机尾传动系统最大输入转速3 319 r/min为输入，以其最大传递扭矩1 474.4 N·m为载荷，将啮合时变刚度以傅里叶级数的展开形式植入多体动力学模型中进行仿真分析，并与理论计算值进行对比，如表1所示。由表1可知仿真误差在允许的范围内，说明了多体动力学模型正确可靠。

表1仿真模型误差表

Tab.1Comparisonbetweenmodelsimulationresultsandtheoreticalcalculationresults

参数/单位理论值仿真值误差/%啮合频率/Hz1 2721 2720啮合力/(N·m)9 3549 7404.1输出轴转速/(r·min-1)1 192.71 1920.6

3.1 轴系相对位置变化量对齿轮啮合特性的影响

对直升机尾传动系统尾桨轴偏移量分别为0，0.1，0.2，…，0.9 mm，以及倾斜量分别为0，0.1，0.2，…，0.9°时的齿轮啮合力进行了分析。以该型直升机尾传系统最大输入转速和最大载荷时的工况进行仿真设置。得到齿轮啮合力的时频图如图8，9所示。由图8，9可知，直升机尾传输出轴偏移位置变化与倾斜位置变化导致轴系相对位置变化时，尾传螺旋锥齿轮副啮合力在时、频域均有明显变化；倾斜位置变化下，啮合力频域出现明显边频信号，边频幅值甚至大于啮合频率及其倍频幅值。

图8 偏移位置变化下齿轮啮合力时域图和频谱图Fig. 8 Time-frequency map of gear meshing force under offset position change

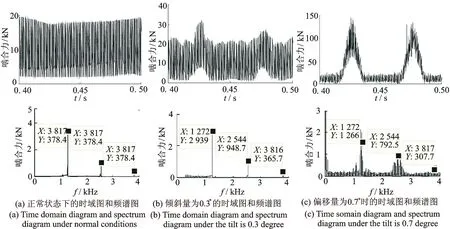
图9 倾斜位置变化下齿轮啮合力时域图和频谱图Fig. 9 Time-frequency map of gear meshing force under tilt position change

平均啮合力随相对位置变化而变化的趋势见图10。由图10可知，平均啮合力随偏移位置增大而减小，源于偏移位置变化导致的齿轮啮合力臂的增加且转矩不变；平均啮合力随倾斜位置增大而增大，开始增大缓慢之后迅速增大，源于倾斜位置变化导致的齿轮对啮合时接触面积减小。

图10 轴系相对位置变化下平均啮合力变化趋势Fig. 10 The tendency of average meshing force under the change of relative position of shafting

3.2 不同载荷下轴系相对位置变化对齿轮啮合特性的影响

当直升机尾传轴系出现相对位置变化时，不同载荷下齿轮的啮合特性也会不同。在该型直升机尾传动系统最大输入转速va=3 319 r/min时，设载荷M=kzMa，kz为载荷系数，Ma=1 474.4 N·m为最大扭矩载荷，令kz=0.1,0.2,…,1.0，仿真分析不同程度轴系相对位置变化下，载荷作用对尾传齿轮对啮合力变化的影响。轴系偏移位置量分别取0，0.2，0.5，0.8 mm，倾斜位置变化量分别取0,0.2,0.5°，0.8°时，不同载荷对尾传齿轮对平均啮合力的影响如图11所示。

图11 轴系不同相对位置变化量下齿轮啮合力随载荷的变化Fig. 11 Variation of meshing force of gears with load at different relative positions of shafts

由图11可知，尾传齿轮对平均啮合力随载荷增大而增大，且呈近似线性关系；由各图线斜率可知，存在轴系相对位置变化时，载荷变化作用下平均啮合力变化速度略大于正常轴系状态，但不同轴系相对位置变化程度下平均啮合力变化速度相当。

3.3 不同转速下轴系相对位置变化对齿轮啮合特性的影响

当直升机尾传齿轮轴系出现相对位置变化时，转速的变化对齿轮的啮合特性也会有影响。在该型直升机尾传系统最大扭矩载荷为Ma=1 474.4 N·m下，设尾传输入转速v=ksva，ks为转速系数，va=3 319 r/min为最大输入转速，令ks=0.1,0.2,…,1．0，仿真分析不同程度轴系相对位置变化下，输入转速对尾传齿轮对啮合力变化的影响。轴系偏移位置量分别取0，0.2，0.5，0.8 mm，倾斜位置变化量分别取0，0.2，0.5，0.8°时，不同转速对尾传齿轮副平均啮合力的影响如图12所示。

图12 轴系不同相对位置变化量下齿轮啮合力随转速的变化Fig.12 Variation of meshing force of gears with speed at different relative positions of shafts

由图12可知，无轴系相对位置变化时，尾传齿轮对平均啮合力不受转速影响；轴系偏移位置变化下，齿轮对平均啮合力受转速影响较大，随转速的增大而明显增大；轴系倾斜位置变化受转速影响较小，倾斜位置较大时，随转速增大齿轮对平均啮合力缓慢增大。

4 结束语

笔者以某型直升机尾传动系统——轴系相互垂直的螺旋锥齿轮系为对象，研究了旋翼轴偏移位置变化和倾斜位置变化导致的轴系相对位置变化下齿轮对啮合力变化规律。通过将轴系相对位置变化转化为齿轮对间隙的变化，进而转化时变啮合刚度和啮合阻尼的变化，建立轴系相对位置变化的动力学模型，分析了不同轴系相对位置变化量、不同载荷、不同转速下，齿轮对啮合力变化规律，发现：a.平均啮合力随偏移位置增大而减小，随倾斜位置增大而增大。b.平均啮合力随载荷增大而增大，且呈近似线性关系；存在相对位置变化时，平均啮合力变化速度略大于正常轴系状态，不同相对位置变化程度下，平均啮合力变化速度相当。c.轴系偏移位置变化下平均啮合力随转速的增大而明显增大；轴系倾斜位置变化下平均啮合力随转速增大缓慢增大。

本研究工作可为直升机尾传动系统运行状态监测提供理论依据，确保其安全高效运行等,具有重要意义。