使用应变模态和遗传算法的有限元模型修正方法*

展 铭， 郭勤涛， 岳 林， 张保强

(1.南京航空航天大学机电学院 南京，210016) (2.厦门大学航空航天学院 厦门，361005)

引 言

在机械、土木、航空航天以及武器装备等领域的结构设计和研发过程中，建模和仿真分析已经成为了一种重要的手段[1]。随着结构设计对仿真分析的重视，仿真模型的精度越来越受到人们的关注。在建立结构有限元模型时，模型中的参数大多是建模者根据相关手册或是自身的经验设定，这必然会导致所建模型与真实模型的响应存在一定的误差，从而使得基于模型的结构响应预测偏离结构的真实响应。模型修正是根据结构试验信息对仿真模型中的参数进行校准，从而达到缩小仿真分析和试验测试之间误差的目的的过程。

有限元模型修正可以分为矩阵型和参数型两大类。矩阵型方法[2]直接对结构的质量矩阵和刚度矩阵进行修改，修正后的矩阵往往不具备带状稀疏性，使得其物理意义不明确，因此该方法的应用较少。参数型方法将模型中的几何、材料属性、连接刚度等参数作为待修正变量，通过构造优化问题并采用灵敏度分析方法或优化设计方法，获得使仿真分析和试验测试误差最小的参数组合，从而达到修正的目的[3]。近年来，有限元模型修正吸引了众多学者的关注。在修正参数选择方面，姜东等[4]从结构固有频率的能量法出发，研究了模型修正中参数选择的方法。Calvello等[5]采用逆分析方法选择模型修正中误差的敏感参数。在修正的响应量选取方面，张保强等[6]用模态频率和有效模态质量误差的残差，基于遗传算法实现了梁结构的修正。Sanayei等[7]采用静态和模态试验数据修正桥梁结构的质量和刚度。Guo等[8]基于应变频响函数的相关性实现了有限元模型修正。在修正策略方面，针对复杂连接结构，朱跃等[9]采用分层思想将复杂结构分成多个子结构，分别对子结构进行修正，并将修正后子结构参数带入到整体结构中，实现了整体结构的修正。基于约束子结构思想，杨秋伟等[10]实现了基于局部子结构静态响应修正的约束子结构法。Xiao等[11]提出了Bayes-Kriging的修正方法。大型复杂工程结构的模型修正过程往往计算成本较大，Ren等[12]用响应面代替有限元模型，实现了基于静态响应的模型修正。方剑光等[13]基于代理模型，实现了汽车悬架的多体动力学模型修正。Li等[14]结合模型降阶技术提出了一种新的模型修正迭代方法。关于模型修正更好的理解可以参阅文献[15]。

上述文献多数是使用振动响应，如模态频率、加速度、位移等进行修正。在工程实践中会出现响应对局部状态参数不敏感的情况，从而导致修正过程无法得到合理的应力分布准确模型。此外，在多数情况下修正后的模型用于强度分析或结构优化设计，选择一种能够同时反映结构全局特征和局部状态的响应对于有限元模型修正至关重要。应变模态包含结构全局的频率信息和能够表征结构局部状态的应变振型信息，可以将其作为有限元模型修正的目标响应。

笔者以应变模态为目标响应量，采用仿真和 “试验模型”的应变模态频率误差及模态置信度误差，构造待修正的目标函数。采用遗传算法，搜索目标函数的最小值，获得稳定收敛的待修正参数组合，并对修正结果进行了验证。

1 应变模态

1.1 应变模态推导

在有限元中，单元节点的位移向量和单元内任一点的位移向量存在如下关系

(1)

根据应变是位移的一阶导数关系可知，单元n内任意一点的应变εn可表示为

(2)

其中：Bn为单元应变矩阵，描述位移与应变之间的变换关系。

对于结构整体而言，式(2)可写为

ε=Bφe

(3)

其中：ε为结构中所有点的应变值；B为结构整体应变矩阵；φe为结构所有单元的节点位移。

记总体坐标中节点位移向量为φs，局部坐标和总体坐标系之间的转换矩阵为T，则存在如下的转换关系

φe=Tφs

(4)

将式(4)代入式(3)中可得

ε=BTφs

(5)

多自由度系统的振动方程为

(6)

其中：M，C，K分别为结构的质量、阻尼和刚度矩阵；f为外载荷。

令f=Fejωt，则φs=Usejωt，代入到式(6)中可得

(-ω2M+jωC+K)Us=F

(7)

由模态叠加法可知，式(7)的解为

(8)

其中：φ=diag(φ1,φ2,…,φk)为结构的位移模态振型；Y=diag(Y1,Y2,…,Yk)，且Yi=(-ω2mi+jωci+ki)-1。

将式(8)结合φs=Usejωt代入式(5)中可得

ε=BTφYφTFejω t=ψεYφTFejω t=

(9)

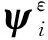
1.2 应变模态置信度

根据结构动力学可知，结构的位移模态振型以及应变模态振型均具有正交性。但是，由于仿真分析中的参数设置以及试验测试中的传感器配置、噪声干扰等因素的存在，导致仿真分析的应变模态和试验测试的应变模态振型之间可能存在差异。Allemang[16]等提出了一种评价位移模态相关性的方法，即位移模态置信度(displacement modal assurance criterion,简称DMAC)，借鉴该方法笔者采用应变模态置信度(strain modal assurance criterion,简称SMAC)评价仿真分析和试验应变模态振型的相关性，其计算方法如下

(10)

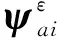
模态置信度矩阵的对角线元素越接近于1且非对角线元素越接近于0，表明仿真分析和试验测试的应变模态振型相关性越高。在工程实践中，要求模态置信度矩阵对角线元素大于0.7，且非对角线元素小于0.2。

2 结构动力学模型修正基本理论

2.1 模型修正方法

有限元模型修正属于典型的动力学反问题，可以归结为如下的优化形式

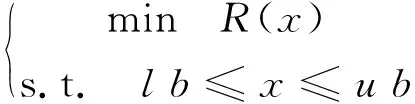
(11)

其中：x为待修正参数；lb和ub分别为x的下限和上限；R(x)代表待修正的目标，常为仿真模型和试验测试对应的特征量残差的函数。

结构前m阶应变模态的频率相对误差为

(12)

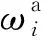
结构前n阶应变模态置信度相对误差为

(13)

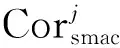
2.2 遗传算法

随着学科交叉融合，研究者受自然规律等的启发，设计了多种智能优化算法。遗传算法是根据生物进化论和遗传规律提出，其实现过程不需要求解目标函数的导数信息，具有搜索目标函数全局最优解的能力，基本实现步骤如下：

1) 数码转换，即在优化前将可行域按照一定的原则转换到遗传算法能够识别和计算的数码形式，完成优化后再将其转换成十进制编码的可行解;

2) 适应度评价，即根据适应度函数判断变量更新时种群中某一个体相对于其他个体的优劣程度;

3) 遗传操作，指模仿生物进化过程对变量个体基因进行的变换，包含选择、交叉和变异3种方式。

图1 加筋壁板有限元模型Fig.1 Finite element model of stiffened wall plate

3 算 例

加筋壁板结构广泛应用于航空航天、机械工程等领域，主要包括底板、夹持边以及加强筋三部分，夹持边和加强筋通过机械连接与底板相连。在Nastran中建立某加筋壁板结构的有限元模型，如图1所示。模型中底板、夹持边以及加强筋采用二维四边形单元描述，连接部分采用bush单元描述，且夹持边、加强筋与底板的连接刚度分别设为两组不同的参数。

将加筋壁板有限元模型中的材料弹性模量、夹持边与底板连接的法向和切向刚度、以及加强筋与底板连接的法向和切向刚度作为待修正参数。本研究使用应变模态作为响应的模型修正方法，通过改变模型中待修正参数值并在对应模型计算的应变模态振型中加入5%的高斯白噪声模拟试验测试及模态识别过程中的误差，构造用于修正的“试验模型”。采用结构的前6阶模态作为修正的目标响应，根据第2节中应变模态频率误差及应变模态置信度误差的定义，采用两种误差的加权和作为待修正的目标函数，即

f(x)=W1Eω+W2Esmac

(14)

其中：f(x)为用于修正的目标函数；Eω，Esmac分别为应变模态频率误差和应变模态置信度误差；W1，W2分别为应变模态频率误差和应变模态置信度误差的权重，在文中两权重值均取为1。

模型修正最基本的要求是复现用于修正的响应特征，更重要的是对于其他响应特征量的预测。将修正后的待修正参数值代入加筋壁板有限元模型中，并采用结构的第7～10阶应变模态验证修正后模型的精度。有限元模型修正前后，加筋壁板的前10阶频率及误差如表1所示。

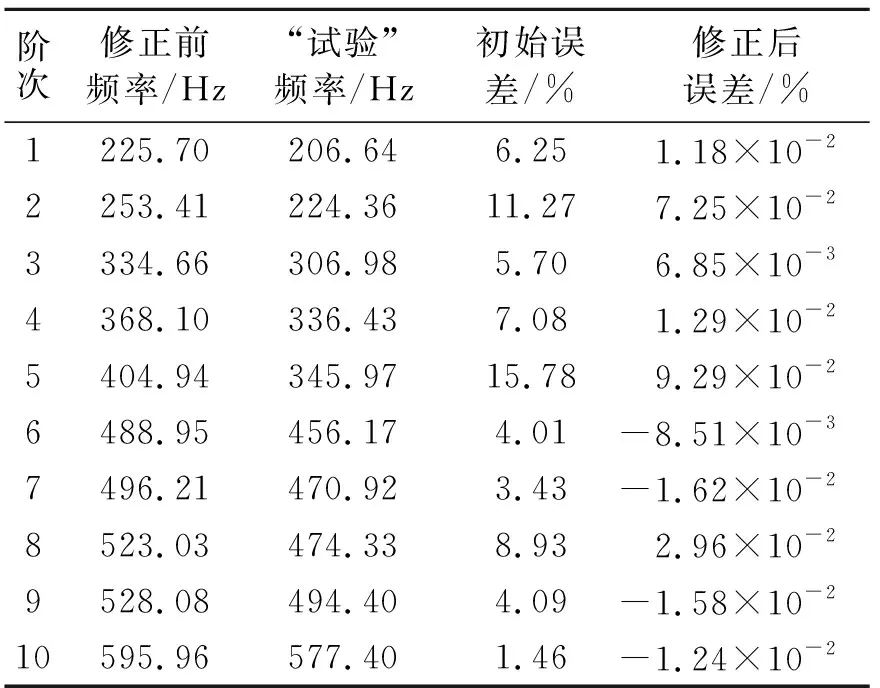
表1 修正前后结构频率及误差

从表1所示的频率误差可以看出，经过有限元模型修正，在修正频段内应变模态频率最大误差从15.78%降为9.29×10-2%，频率绝对平均误差从8.35%减小到3.42×10-2%。在修正频段外，结构预测的频率最大误差从8.93%降为2.96×10-2%，预测频率的绝对平均误差从4.48%减小到1.85×10-2%。表明修正过程有效降低了有限元模型仿真频率误差，修正后有限元模型不仅能够复现修正频段内的应变模态，同时也具有一定的外推预测能力。

有限元模型修正前后，加筋壁板的前10阶位移模态置信度DMAC以及应变模态置信度SMAC矩阵对角线值如表2所示。

表2 修正前后结构模态置信度

从表2所示的应变模态MAC值可知，经过修正后仿真分析和“试验模型”之间的位移振型和应变振型置信度均有显著提高，修正后的模型接近“试验模型”。此外，表2中的模态置信度显示，用于修正的6阶模态中有4阶位移模态置信度大于0.95，而应变模态置信度相对于位移模态整体偏低。上述数据表明，待修正参数改变会引起应变模态置信度值发生更大的改变，即应变模态置信度相对于位移模态置信度对结构参数改变更为敏感。

4 结束语

笔者将应变模态置信度作为有限元模型修正的目标响应量，采用应变模态频率和应变模态振型相关性误差构造目标函数，基于遗传算法实现了一种有限元模型修正方法。以某加筋壁板结构为研究对象，对结构中的参数进行了修正，验证了所提方法在复杂结构有限元模型修正的正确性和可行性,并得到如下结论：a.模态置信度不仅可以用于评价两个模型对应模态振型的相关性，同时也是有限元模型修正中的实用性很强的一类综合响应特征，并且应变模态置信度比位移模态置信度对结构参数的改变更为敏感；b.在修正频段内，所提方法降低了初始模型和“试验模型”之间的误差，有效复现了修正频段内的应变响应；c.修正后的有限元模型具有一定的外推预测能力，能够较准确地预测修正频段外的结构应变响应。