置信度条件下轴承寿命的可靠度分析

2015-07-25余挺

轴承 2015年2期

余挺

(上海通用轴承有限公司，上海 200240)

1 可靠度和置信度的关系

汽车制造商对轴承寿命一般会提出以给定的置信度CY达到可靠度RX的要求，记为RX/CY。例如R90/C90，表示轴承寿命的要求是在90%的置信度下达到90%可靠度。这种要求比普通的不带置信度的可靠度要求更为严格。

可靠度是零件满足确定的寿命要求的可靠程度，而置信度是零件试验样本试验结果的可信程度。例如，对20个一组的样本试验，具有90%置信度和90%可靠度的试验结果，表示每组试验后将有2个零件失效，如果进行10组这样的试验，则有9组样本试验后失效零件不超过2个。

可靠度R在单侧置信度为1-α置信区间[RL,1]内的概率满足

P(RL≤R≤1)=1-α，

(1)

式中:RL为可靠度的下限值，即零件的最低可靠度。寿命的RX/CY要求，相当于对一个特定的寿命L，要求在置信度CY=(1-α)100%下满足可靠度RX=RL。

文献中已有采用Bayes方法进行可靠度和置信度分析的论述[1]。假设θ服从先验分布π(θ)，θ的取值范围为Θ，通过随机抽样得到一组数据x，其分布函数为f(x|θ)，根据Bayes公式可得到参数θ的后验分布为[2]

(2)

假设轴承达到规定寿命L的可靠度R的先验分布服从[0，1]均匀分布，则N个相同轴承如果在L时间内全部没有失效，按N重伯努利试验理论，x服从二项分布,根据(2)式，已知抽样数据x=N,R的后验分布为

(3)

因此，

(4)

式中：C为可靠度介于RL和1之间的置信度，以下简记RL为R。由(4)式可以看出，如果试验次数较少，即使可靠度很高，相应置信度也并不高。例如，N=1，R=0.9时，C=0.19。只有当N增加到一定值时，才会使C明显增加,例如，N=21，R=0.9时，C=0.90。

另一方面，R虽然服从[0，1]均匀分布，似乎为很宽松的假设，与轴承预计的计算额定寿命(R=0.90)存在差异。但从R的Bayes估计[3]

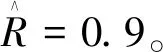
2 基于RX/CY的设计

给定轴承目标寿命L1的RX/CY要求，轴承设计任务之一是要计算轴承的额定寿命。已知寿命L1的可靠度为RX，即可按标准ISO 281：2007由下式求出所需的额定寿命LRX,

L1=a1LRX，

式中：a1为可靠度修正系数。

在额定寿命LRX基础上，进一步确定满足置信度要求的额定寿命。假设寿命L满足二参数Weibull分布(三参数Weibull分布可类似讨论)，其可靠度可表示为

(5)

式中：b为Weibull分布斜率；V为Weibull分布的特征寿命。由(4)和(5)式得

上式可变为

(6)

一般而言，置信度与试验的结果有关。RX/CY的可靠度要求是基于样本试验结果的一种判断，要求样本统计意义的可靠度应落于置信度为CY的[RX,1]置信区间内。一组样本的试验结果满足Weibull分布时，可在相应的Weibull分布概率纸上用点表达试验结果，按试验寿命的大小排序编号，第j号样本所在点的纵坐标为第j顺序秩的中间秩[4]。中间秩是置信度为50%的顺序秩的估计值。所有中间秩确定的试验结果点拟合出来的曲线就是通常的试验产品的Weibull分布曲线，体现了产品内在固有的寿命分布，而正常情况下设计结果应该反映产品内在固有的寿命分布。因此，对以上基于RX设计的额定寿命LRX,其置信度可假定为50%。

如果确定LRX的置信度为50%，则(6)式变为

(7)

为进一步获得满足RX/CY要求的额定寿命LRX/CY，设新的寿命分布可靠度为

(8)

一般总有CY>C50,故LRX/CY>LRX,进而易知，V1>V,但LRX/CY是待定的，另设N不变，故下式仍能类似(7)式成立

(9)

从(7)和(9)式可得

(10)