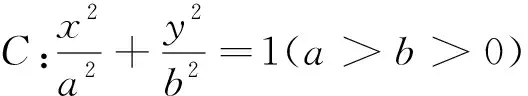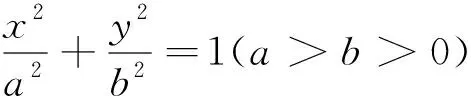圆锥曲线问题的探究

山东省聊城大学数学科学学院 (252000)

张 鑫 于兴江

圆锥曲线既是平面解析几何教学中的重点、难点,又是高考中重点考查的对象.圆锥曲线的第二定义也称其为统一定义,将圆锥曲线和准线、焦点巧妙地联系起来.基于此,本文利用几何画板对圆锥曲线问题进行探究.

圆锥曲线(椭圆、双曲线、抛物线)统一定义[1]：平面内与一个定点和一条定直线的距离之比为常数e(e>0)的点的轨迹,称为圆锥曲线.其中定点是圆锥曲线的焦点,定直线是对应于焦点的准线,e为离心率.

注：当e>1时,该轨迹为双曲线；当e=1时,该轨迹为抛物线;当0

图1

定理设圆锥曲线c的焦点为F,过焦点F且不垂直于含有焦点的对称轴的直线l与圆锥曲线C交于M、N两点,点N关于该对称轴的对称点为N′,则直线MN′恒经过准线与对称轴的交点Q,过点Q的对称轴的垂线就是圆锥曲线的准线.

当k=0时,直线l:y=0,点N与N′重合,则直线MN′与l重合.由此可推得,若直线MN′经过定点,该定点必在x轴上.

当k≠0时,联立直线与椭圆的方程,消去y得(b2+a2k2)x2-2a2k2cx+a2k2c2-a2b2=0.

双曲线、抛物线的证明方法与椭圆证明方法类似,不再赘述.

(1)求椭圆的方程；

(2)直线l过椭圆的右焦点F且不垂直于x轴,l与椭圆交于点M、N,设点N关于x轴的对称点为N′,问：直线MN′是否经过定点？若经过定点,请求出；否则,说明理由.

推论设圆锥曲线C的准线与对称轴的交点为Q,过Q的直线l与圆锥曲线C交于M、N两点,点N关于该对称轴的对称点为N′,则直线MN′与对称轴的交点为焦点F.

由圆锥曲线的第二定义、定理及推论,易知圆锥曲线、焦点和准线中的任意两个要素,都可以求出另外一个要素.