以2017年全国新课标Ⅰ为案例解读“学业水平考试与高考命题建议”

安徽省芜湖十二中 (241100)

金 奎

《普通高中数学课程标准(2017年版)》与《普通高中数学课程标准(实验)》相比，主要有三点变化：

变化1：将“教学建议”“评价建议”合二为一，变为“教学与评价建议”;

变化2：增加了“地方与学校实施课程标准的建议”.具体从“地方实施课程标准应注意的四个问题”、“学校实施课程标准应注意的四个问题”、“教师实施课程标准应注意的五个问题”进行了阐述；

变化3：增加了“学业水平考试与高考命题建议”.对高中毕业的数学学业水平考试、数学高考的命题提出了以下三点建议.

建议①：命题原则，命题应根据学业质量标准和课程内容，注重对学生数学学科核心素养的考查，处理好数学学科核心素养与知识技能的关系，充分考虑对教学的积极引导作用.在传统评分的基础上，根据解题情况对学生的数学学科核心素养水平的达成进行评价(参见案例20～35).

建议②：考试命题路径,基于数学学科核心素养的考试命题，注意构建数学学科核心素养的评价框架，依据评价框架，统筹考虑三个维度(第一个维度是反映数学学科核心素养的四个方面，它们分别为情境与问题、知识与技能、思维与表达、交流与反思；第二个维度是四条内容主线，他们分别是函数、几何与代数、概率与统计、数学建模活动与数学探究活动；第三个维度是数学学科核心素养的三个水平)，编制基于数学学科核心素养的试题，每道试题都有针对性的考查重点.对于每道试题，除了给出传统评分标准外，还需要给出反映相关数学学科核心素养的水平划分依据.

建议③：说明，在命题中选择合适的问题情境是考查数学学科核心素养的重要载体，应特别关注数学学习过程中思维品质的形成，关注学生会学数学的能力.

下面我们通过2017年全国新课标Ⅰ高考题为案例来分析《普通高中数学课程标准(2017年版)》中“学业水平考试与高考命题建议”所体现的变化.

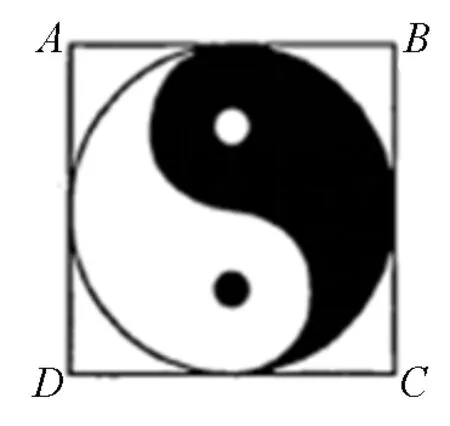
图1

案例1 (2017年全国新课标Ⅰ第2题)如图1，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是( ).

命题原则：注重对数学学科核心素养中直观想象考查，处理好数学学科素养与几何概型知识的关系，充分考虑对几何概型教学的积极引导作用，结合中国古代的太极图关注学生对数学内容的直观理解，让同学们充分理解样本点和无限样本空间的含义，加深了对几何概型的理解；既充分考虑高中学生的接受能力，更注重学生数学学科核心素养的提升；很好体现数学文化是指数学的思想、精神、语言、方法、观点以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义以及与数学相关的人文活动，通过高考引导同学们重视和弘扬中国优秀传统文化.

考题路径：本题反映数学学科核心素养的“情境与问题、知识与技能”两个方面，紧扣“概率与统计”这条主线，考查学生的数学文化和直观想象数学核心素养，突出文化教育的重要地位，丰富充实加强中华优秀传统文化教育的相关内容，加强学生对中华传统文化的深入学习和思考，形成正确的世界观、人生观和价值观，从而充分发挥数学教育的育人功能，达到立德树人，增强文化自信的目标.

说明：本题从学生熟悉的现实情境和数学情境入手，考查同学们概率统计知识点，突出数学应用和实际应用的内在联系，在今后的教学中，我们需要丰富充实加强中华优秀传统文化教育的相关内容.本题在高考中以第2题出现，难度为简单题，属于送分题，让学生在考试中能得分，稳定学生的情绪，有利于学生进入状态，发挥正常水平，以传统文化的情境出现考察概率统计中几何概型知识点.

案例2 (第12题)几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N：N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( ).

A．440B．330C．220D．110

2017年高考第12题承载落实立德树人的根本任务，大学生需要有家国情怀，响应国家号召，到祖国最需要的地方去贡献自己的力量.试题设计从现实情境入手围绕高中数学的核心内容，突出考查学生的数列知识，彰显了《普通高中数学课程标准(2017年版)》提出数学学科核心素养，突出数学学科素养的“逻辑推理、数学运算、数据分析”三个维度.试题设问及解答方式有创新，主要考查学生数学逻辑思维能力，提升学生的数学核心素养；试题背景贴近学生的生活实际，从学生熟悉的情境入手，运用数列解决实际问题，体现数学的应用价值；此题还有寓意就是与新课程的案例37完美对接，通过高考引导作用让学生了解互联网+，在今后的学习中可以充分利用互联网+进行学习，教师可以尝试线上、线下平台开展丰富多彩的教学活动，不断探索创新，改变教学方式；本题作为选择题的压轴题同样发挥高考选拔人才的功能.

案例3 (第19题)为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸(单位：cm)．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2)．

(1)假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在(μ-3σ，μ+3σ)之外的零件数，求P(x≥1)及X的数学期望；

(2)一天内抽检零件中，如果出现了尺寸在(μ-3σ，μ+3σ)之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．

(ⅰ)试说明上述监控生产过程方法的合理性；

(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸：

9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04

10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95

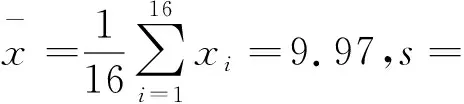
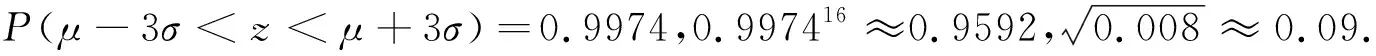
命题原则：注重对数学学科核心素养中数学建模、数学运算、数据分析等维度考查，处理好数学学科素养与概率统计的关系，大数据分析积极引导作用，结合概率统计关注学生对数学内容的深入理解，让同学们充分理解正态分布和统计中数字特征的含义，让学生初步接触大数据分析，同时为高等教育中的概率埋下伏笔，同时要充分考虑高中学生的接受能力，以发展学生的数学学科素养为导向，创设学生熟悉的情境，启发学生思考，引导学生把握概率统计的数学教学本质.

考题路径：本题在高考中以难题姿态出现，经历十余年的高中课程改革实践，在全面推进素质教育中发挥了重要作用，但是，面对社会经济、科技文化发生的巨大变化，对人才培养提出的更高要求，还有一些不相适应和亟待改进之处，需要进行修订完善.现在我国已弯道加速进入互联网+时代，需要学生了解、接受、并能融入大数据信息互联网时代，所以本题从现实生活中常见的情境入手，很好的考查概率统计的知识，让学生通过具体示例，掌握二项分布及其数字特征并能解决简单的实际问题，通过误差模型，了解正态分布、正态分布的均值、方差及其含义，了解正态分布的特征；通过此题让学生参与数据分析的全过程，并鼓励学生独立的处理数据，引导学生利用所学的知识解决生活中的实际问题，并适当进行严格、准确的数据描述.本题重点考查了概率统计的知识点，难度很大.

说明：数学学科高考命题建议提出，命题时，应有一定数量应用问题，还应包括开放性问题和探索性问题，重点考查学生的思维过程、实践能力和创新意识，问题情境的设计应自然、合理.增强了数学测试的可操作性，进一步明确和加强了与高考的联系，更能适应新形势下新课程、新考试的需要.从学生角度本题划分为难题，肩负选拔人才的重任，让学生从自然、合理的情境入手，经历、体验、探索大数据处理问题，需要学生掌握概率统计的知识点，重点考查学生的思维过程，并能运用此知识点解决实际问题，从而培养学生实践能力，极大提升学生创新意识.

《普通高中数学课程标准(2017年版)》增加了“学业水平考试与高考命题建议”，在今后的教学中对我们一线教师有方向性指导意义，我们要以此为根本，及时调整教学手段、教学内容，评价方式.