例谈数学解答题的优解策略
2018-10-30山东省寿光中学262704
山东省寿光中学 (262704)
李元卓
在平时练习或考试中,常常遇到一些有难度或者有疑惑的题目,尤其是解答题,作为考试命题的主要题型,往往具有一定的难度和较大的运算量,有时难免陷入困境.能否迅速找到恰当的方法,及时突破困境,直接影响着解题速度和成绩的高低.为此我们将从以下几个方面谈谈如何突破困境,及时找到最优解法,希望对大家有所启示.
一、研究题目图形,探求解题方法
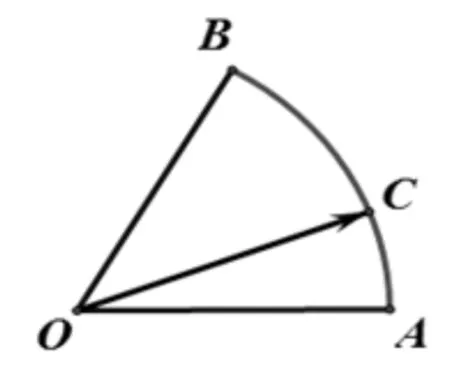
图1
有些数学题是通过图形给出的.解决这类问题,应该仔细研究题目图形,从图形的特点入手,寻找解题的突破口.
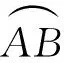
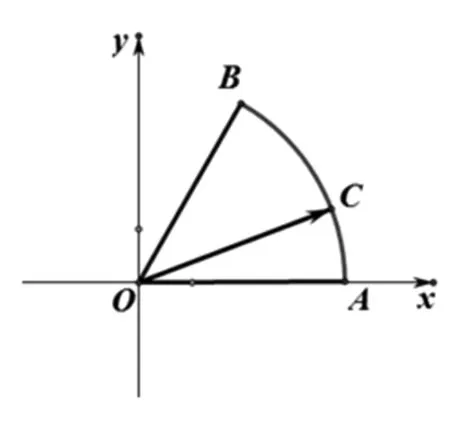
图2
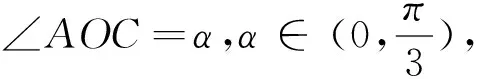


二、观察题目结构,实现解题突破

例2 已知f(x)=x2-x+c的定义域为(0,1),x1,x2∈(0,1)且x1≠x2,证明|f(x1)-f(x2)|<|x1-x2|.
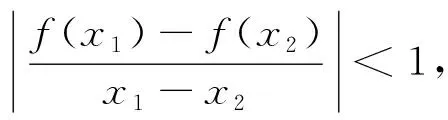

一般来说形如|f(x1)-f(x2)|≤m|x1-x2|(m>0)型的不等式问题都可以利用上述方法求解.
三、着眼数量关系,寻求恰当方法
有些题目,乍看比较繁杂,一时难以入手.但如果仔细分析题目所给出的数值或变量,找出数量之间存在的一些特定的关系,就可以找到合适的解题方法.
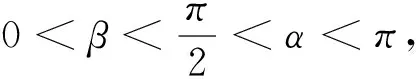

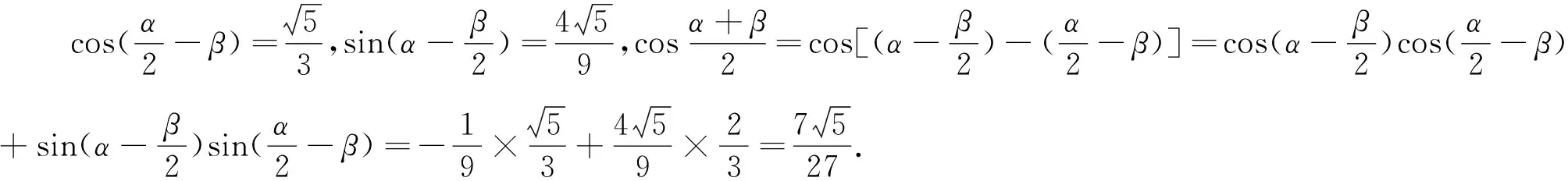
四、正面思路受阻,逆向思维突破
有些题目从正面解题可能比较麻烦,甚至难以找到解题思路,这时不妨从逆向入手,寻找解决问题的思路和方法.
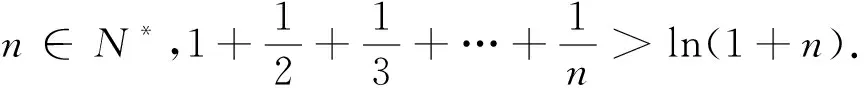
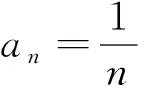
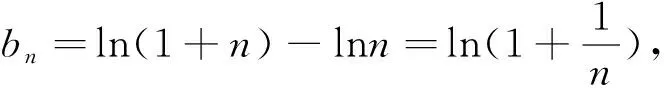
实事上,很多形如f(n)>g(n)型不等式的证明问题都可利用上述方法求解.
五、变换问题角度,突破解题困境
有些数学题目,或者难以解决,或者解题过程繁杂,按照常规思路容易陷入解题困境.但若变换一下问题角度,则可能会变得容易一些.
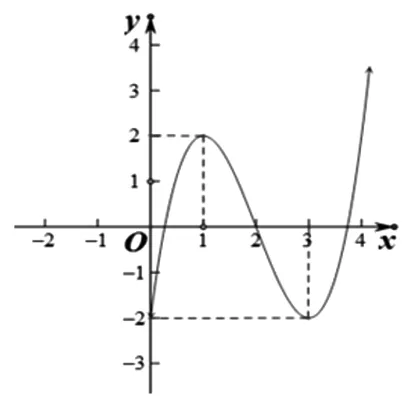
图3
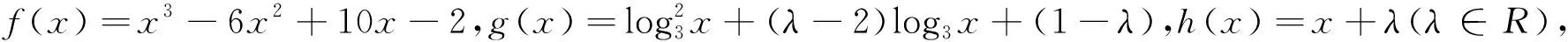
分析:根据f(x)=h(x),得x3-6x2+9x-2=λ.令φ(x)=x3-6x2+9x-2,则φ′(x)=3x2-12x+9,由φ′(x)=0得x1=1,x2=3,所以φ(x)极大值=φ(1)=2,φ(x)极小值=φ(3)=-2,结合如图3可知当-2<λ<2时f(x)=h(x)有三解.于是问题转化成为当λ∈(-2,2)时,g(x)<0恒成立,求x的范围.
以下再按常规思路不易解决,但可以变换一下问题角度,把λ视为主变量,x为参数,将问题转化为关于λ的函数g(λ)=(log3x-1)λ+(log3x-1)2,当λ∈(-2,2)时恒有g(λ)<0.因g(λ)的图像为一直线,于是g(±2)<0,即
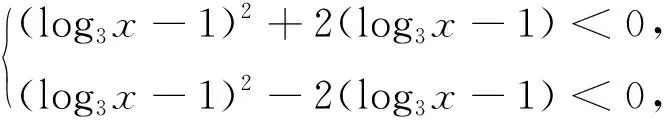
六、挖掘隐含条件,优化解题方法
有些题目的条件中,隐含着便于解决问题的某些条件或方法暗示,若能从中找出来,对问题的解决会十分有利.
例6 已知x1,x2是关于x的二次方程x2+ax+b=0有两个实根,且|x1|<2,|x2|<2,求证
2|a|<4+b.
分析:解决此题关键是能从|x1|≤2,|x2|≤2中挖掘出“函数f(x)=x2+ax+b的两个零点都落在(-2,2)之间”这一条件,利用一元二次函数零点的分布来解决,其他任何解法都非常繁琐.
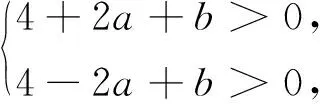
七、两头分别入手,中间步步联系
有些给条件的求值或证明问题,在条件和结论中都可能存在很多信息,这时可以根据已掌握的知识,将条件和结论尽情发散出去,条件可能派生出若干结论,结论也可呈现多种形式,只要两者能够联系起来,问题就能得到解决.
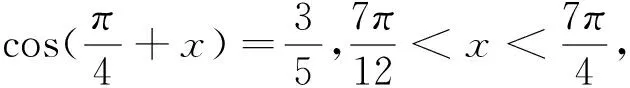
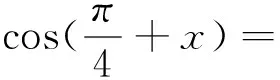
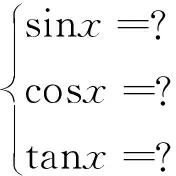
再将结论发散开来:

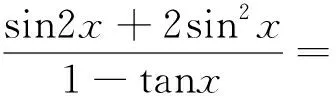
从上述分析可以看到,从条件式入手推出了多个不同的结论.将结论式变形又得到了多种形式,只要从①②③等结论中找出与(1)(2)(3)…等形式匹配的式子,问题就得以解决.匹配的式子越多,题目的解法也就越多.就本例而言,可以找出的解法太多了,请同学们自己选择适当的方法求解.
八、利用等价转化,巧妙化归迁移
我们经常会遇到一些求解参数范围的题目,有的甚至含有多个参数,这类问题就要不断地将知识进行迁移,逐步化归成我们熟悉或易于解决的问题.
例8 已知函数f(x)=lnx-ax2-a+2,其中a∈R,若存在x0∈(0,1],使得对任意的a∈(-2,0]不等式mea+f(x0)>0(其中e为自然对数的底数)都成立,求实数m的范围.
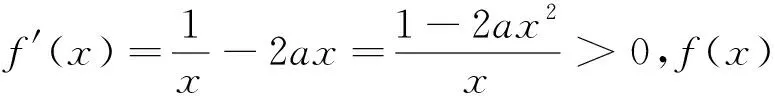
从以上几例可以看出,及时找到解题突破口,选取适当的解题方法,对于提高解题速度,优化解题过程,提高数学成绩,无疑是十分有益的.因此,在平时的学习中,我们应该积极探索归纳解题规律,熟悉必要的技巧,不断提高自己分析问题和解决问题的能力.
