“多元齐下，扬长培短”

陈来源

摘 要：本文以应用题教学为例，探讨在小学数学教学中如何应用多元智能与学习风格整合理论，实现教学质量的提升。多元智能与学习风格整合理论注重发挥学生的个性特长，激荡他们的思维火花，使基础不同的学生得到不同程度的提高。

关键词：多元智能理论；学习风格理论；小学数学；应用题教学

传统的应用题教学特别注重抽象的数量关系分析，在学生不能充分理解的情况下教师往往只能让学生按照某个固定模板去列出算式，因此数量关系分析被不少教师当成了传统教学缺乏生机的代名词。目前的教师普遍过分注重问题情境的华丽，让学生跟着感觉走，即使学优生能对解题方法一目了然，但基础薄弱的学生只能是稀里糊涂、一筹莫展，最终只会让两极分化更为严重，这说明应用题教学正从一个极端走到另一个极端。

如何破解这一现实难题？笔者本校将多元智能理论与学习风格两个理论整合起来，在此基础上进行应用题的数量关系分析，对此开展了课题研究。

多元智能理论由美国心理学家加德纳创立，他认为人的智能结构并非是单一智能，而是由数理、语言、运动、空间、音乐、人际等8种元素组合而成的多元智能。习瓦尔与汉森则提出一个以过程为导向的学习风格模型，把人们的智能分为掌握型、表达型、理解型、人际型四种类型。把这两条理论整合起来，在教学实践中加以总结，我们称之为多元智能与学习风格整合理论。以下，笔者通过以应用题教学为例作具体探讨。

一、摆脱教材框架，多元激发兴趣

现行的小学数学教材往往在每一课的开头设计有一定的情境性的内容，可被教师利用来导入教学。但这部分固定内容由于学生早已看到，新鲜感早已消失殆尽，更何况教材所能提供的信息也比较单一；也有不少教师热衷于通过图片、动物故事的形式导入教学情境，但最终学生感兴趣的只是情境本身，而不是数学。上述这两类教学都难以满足不同学习风格学生的需求，教师很有必要对导入策略进行重新思考，从本质上打开学生对数学学习的兴趣。如在教学用百分数解应用时，笔者出示了如下习题：

（1）计算以下方程式：15x-x=2.8；x+30%x=26；x-15%x=34。

（2）分组讨论说明以下数量关系：北海公园有罗汉松40棵，樱花树比它多40%；六年级班里女生比男生少10%；今年小红家的生活开支比全家总收入低30%；小明比去年又长高了10%。（这道题我们允许学生用语言组织的形式描述以上提及的数量关系，也可以用画图、线段图等方式来体现）

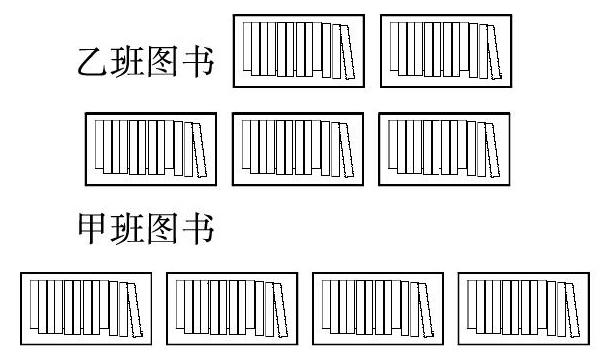
（3）列方程解应用题：甲班图书角的图书比乙班少12本，甲班图书角的图书数是乙班的五分之四，请问两班的图书数各是多少本？

乍一看，上述设计有点题海战术的味道，而且没有明确的故事情境，没有一丝童趣与生动感。其实并不是这样，这里通过循序渐进的习题设计，“捂热”了知识基础，为百分数应用题教学的主旋律的呈现提供了轻松愉快的前奏。这里引导学生用自己的理解对原有知识做出说明，学生表达自己观点的方法可以是口头语言，也可以是线段图形式，甚至可以动手操作。

对于第（3）题的解析，我们让学生思考如何用方框代替线段“甲班图书角的图书数是乙班的五分之四”，然后用画图软件画出12本书，通过鼠标拖动的方式，复制出12本书填到方框里，学生在图上就直接计算出了两班图书的数量。由于动用了学生的操作、空间智能，这样抽象思维能力不够的学生理解题目的意思就变得易如反掌了，不同智能类型的学生都有自己可以进入数学的渠道，无疑有助于激发学生的求知欲。

二、打破思维束缚，多元分析题意

解应用题是一种培养学生数理逻辑智能的方式，学生要通过分析建立数学的模型，教师应该努力帮助学生打破解题时的思维定式，创造一个多元的教学空间。比如，在一次复习解决“已知一个量的几倍多（少）几是多少，求这个量”的应用题时，考虑到这类问题往往需要逆向思考，而学生又常常受文字思维定式的影响，凡是“多”一律用加来列式，凡是“几倍”一律用乘来列式，所以教师需要创设帮助学生建立能有助于理解的场景。有一位教师组织了这样的游戏：①同桌两人为一组分别进行闭眼练习单脚站立的游戏，教师数秒数，看大家可以保持平衡的时间有几秒。②把同桌间成绩进行比较，画出线段图。③编应用题，要求说出甲（假设两人中成绩好者是甲）的成绩是几秒，是乙的几倍多（少）多少，然后求乙的时间是多少。④汇报成绩与编题情况。这样的教学充分动用了学生的运动智能、数理智能、空间智能与语言智能，全班学生积极参与其中，可见教师如果能开放思想，学生就能开放想象，即便再复杂的问题也会变得直观形象，易于理解。

三、避免真空解题，多元生活体验

传统教学中的应用题信息往往通过文字来告诉学生，在题海战术的重复操练下，教师只重视对学生数量关系的分析，学生特别重视关键字词的含义，只记住了常规的问题解决的程式，往往把問题情境的特殊情况忽视了。

比如有这样的一道应用题：小明带了18元钱去商场买了5 瓶椰汁，每瓶2.4元，剩下的钱买酸奶，每瓶 2.5元，可以买多少瓶酸奶？很多学生列式计算得到的结果是（18-2.4×5）÷2.5=2.4（瓶），这个结果显然是脱离生活实际的，为了解决这个问题教师可以扮演营业员：“您好，您算得没错，但我们没有0.4瓶的酸奶，请问您有什么办法解决这个问题吗？”这样学生就可以联想到生活中购买商品的数量一般都是整数的情况，体会生活问题的数学策略。再如下面的题目：给长为12.5米，宽为1.3米的靠墙菜地围一段高为1米的篱笆，篱笆的长度有几米？这道题目出现在长方形的周长这一单元里，有学生想当然地列式为（12.5+1.3）×2，而不少学生又感觉到后边还有一个数字“1”的存在，总不能弃之不管吧，于是又有学生列成（12.5+1.3）×2+1，还有的列成（12.5+1.3）×（2+1），学生出现这些问题的原因还在于对所求问题的生活体验不深，造成印象式、死记程式的解题方法。教学时，教师可以引导学生用手势比画，在教室的一角进行演示与想象，让学生发现：①篱笆的长度与高度无关。②靠墙的一面是不用围的。综合运用操作、联想与比较的方法，在解决生活问题的时候学会实事求是，这样学生的数学思维就能走向生活化，告别僵化的教条。

四、解除字面障碍，多元理解运算

为什么不少学困生习惯于把题目中的数据进行东拼西凑，运算符号想到什么就用什么。真正的原因他们是没有了解四则运算的意义。就像本班上的学生，有三分之一的人对加减的意义说不清，有一半的人不知道为何要用乘法。

比如有这样一道题：（1）一块長方形的西瓜地，长40米，宽35米，每0.8平方米种一株西瓜苗，请问这块瓜地一共需要种多少株西瓜苗？学生在列式时拿长与宽相乘这一点普遍没错，可在处理0.8这个数据时问题就多了，有学生认为后边有“一共”二字，就一定要用加法来运算；有的学生认为因为“每”字的存在，就要用乘法运算。对于后者，笔者让他们再次回顾乘法的意义，找到等量关系：每株的面积数×株数=总面积数，需要考虑把总面积40×35=1400（平方米）分为相同的许多块，每块面积是0.8平方米，这里知道了总数与每份数要求份数，所以应该列为40×35÷0.8=1750（株）。可见，只有引导学生真正悟懂运算的意义，才能避免列式错误的出现。为了让学生理解运算的意义，这里可以出示另两道题进行比较：（2）一块长方形的西瓜地，长40米，宽35米，种了1750株西瓜苗，请问平均每株西瓜苗的种植面积是多少？（3）一块长方形的西瓜地，长为40米，种了1750株西瓜苗，平均每株的种植面积是0.8平方米，请问长方形瓜地的宽是多少？这种横向联系无疑对学生理解数理关系与算理非常有益。

除了上述文字形式的换算思考，对于基础薄弱的学生，还可以提供实物图，让他们编几道简单的应用题，帮助他们在直观形象的实际问题中巩固运算的意义。

另外，教师需要适当渗透一些能让学生直观感知的发现错误的能力，这种能力就是我们常说的直觉，比如上述第（1）题如果用乘法计算，无疑会得到一个比总面积数字小的株数，而经验告诉我们，1株西瓜苗种的面积是0.8平方米，2株就是1.6平方米，10株就是8平方米，怎么可能到最后株数比平方数小呢？

几年来，本校借助多元智能与学习风格整合理论，十分注重发挥学生的个性特长，并着手培养学生的短板，做到了“扬长培短”，努力使课堂大餐变“乏味”为“美味”，变“统一餐”为“自助餐”，真正使不同的学生得到不同程度的提高。实践告诉我们，应用题教学不但可以进行数量关系分析，而且需要进行多元化的分析，把学生引向生活本真，培养多种感官参与的综合能力。只有让学生从不同的渠道获取对数量关系的理解，解应用题的能力才能提高，学生也更能接纳自己的优缺点，积极地成长。