非均匀水流中涌浪运动对水下量子通信性能的影响∗

聂敏 潘越† 杨光2) 孙爱晶 禹赛雅 张美玲 裴昌幸

1)(西安邮电大学通信与信息工程学院,西安 710121)

2)(西北工业大学电子信息学院,西安 710072)

3)(西安电子科技大学,综合业务网国家重点实验室,西安 710071)

(2018年1月11日收到;2018年5月5日收到修改稿)

涌浪运动是非均匀水流中的一种非线性运动,是常见的海洋运动形式之一.在进行水下量子通信时,会对光量子信号的传输造成极大的影响.然而,有关涌浪运动造成量子通信信道参数变化的研究,迄今尚未展开.为了研究涌浪运动对水下量子通信性能的影响,首先对涌浪运动的传播建立了数学模型并分析了其频谱特性.针对退极化信道,提出了涌浪运动与水下量子通信信道纠缠和信道容量的定量关系,并对量子密钥分发过程中误码率的影响进行了分析.仿真结果表明,当海面风速在0—20.5 m/s变化时,随着传播周期逐渐增大,信道纠缠度由0.0012逐渐增加到0.8426,信道容量由0.8736减小到0.1024,密钥分发过程中,量子误码率由0.1651增加到0.4812.由此可见,涌浪运动对于水下量子通信性能有着明显的影响.因此,在进行水下量子通信时,应根据涌浪运动的不同程度,自适应调整系统参数.

1 引 言

量子通信作为迄今惟一被证明是无条件安全的通信方式,量子通信技术在金融、军事和政务等领域的应用前景得到了广泛的认可.2005年,潘建伟团队[1]实现了13 km级自由空间的量子纠缠分发和量子密钥分发,首次证实了光子纠缠态在穿越大气层后,其量子性能依然能够发挥作用,并验证了星地之间量子通信的可能性.2010年,由清华大学和中国科技大学组成的科研团队[2],在北京与河北之间成功实现了16 km的量子隐形传态实验.2012年,中国科学技术大学合肥微尺度物质科学国家实验室、中国科学院上海技术物理研究所光电技术研究所等单位组成的联合研究团队又成功实现了100 km级自由空间量子隐形传态和双向量子纠缠分发[3]、星地量子通信的全方位地基验证[4]等重要实验.同年,德国Max-Planck研究所与奥地利量子光学与量子信息研究所(IQOQI)[5]在LaPalMa岛与Tenerife岛之间,实现了自由空间光链路超过143 km的量子隐形传态通信实验,为星地之间实现量子通信奠定了坚实的科学基础.

量子信号在自由空间传输时,必然会受到环境因素影响.文献[6]研究了中尺度沙尘暴对卫星量子通信的影响,为沙尘条件下量子卫星通信的研究奠定了基础.文献[7]介绍了在降雨背景下诱骗态协议最优平均光子数的变色龙自适应策略,依据该算法,可以对每脉冲平均光子数进行调整,使系统的安全密钥生成率得到提升,以此来提高通信质量.文献[8]研究了中纬度地区电离层偶发E层对量子卫星通信性能的影响.这些研究都是在不同环境下,自然因素对量子通信所造成的影响,对于后续研究有着重要的参考价值.

波浪的传播经常受到水流的影响,例如产生Doppler频移效应,顺流时波高减小,波长增大;逆流时波高增大,波长不变.文献[9,10]基于Boussinesq型方程研究了非均匀水流中波浪的传播.涌浪运动是一种常见的非均匀水流运动,涌浪具有较规则的外形,排列比较整齐,波峰线较长,波面较平滑,比较接近于正弦波的形状.早在20世纪50年代,国外学者就提出了几种预报、分析涌浪的理论.Sverdrup和Munk[11,12]从能量的角度去计算涌浪传播中的波高与周期变化以及传播时间.之后也有一部分学者基于实测资料的分析,给出了一些经验性的解释.Bretschneider[13]依据观测资料绘制出了一系列的涌浪特性图例,来解释涌浪在传播过程中的一些特性变化.

2017年8月,上海交通大学金贤敏团队成功进行了首个海水量子通信实验,在国际上首次通过实验验证了水下量子通信的可行性.在实验中,该团队选择光子的极化作为信息编码的载体,并通过模拟证明,在非常大的损耗和散射下,极化编码的光子只会丢失,而不会发生量子比特翻转,而没有丢失的光子可被用于建立安全密钥.目前,国内外还没有展开关于在海水的自然现象下对于量子通信性能影响的研究,因此,本文的研究为水下量子通信系统的性能研究奠定了一定的基础.

本文根据涌浪运动的特性,针对其对于光量子吸收和散射等消光效应的影响,分析了在进行水下量子通信时,对量子纠缠度、量子信道容量、量子密钥分发和量子误码率的影响,分析了涌浪在运动过程中波高及周期对纠缠保真度、信道容量、密钥分发率和误码率之间的定量关系,通过仿真验证,为光量子信号在涌浪运动的条件下进行水下量子通信提供参照依据.

2 非均匀水流中涌浪运动传播的数学模型及其频谱特性

Wang等[14]从势流理论出发,将速度势函数表示为任意水深层处垂向坐标的幂级数,将幂级数代入Laplace方程得到速度势函数的级数解,再将速度势函数表达式代入水底边界条件,并进行截断和引入微分算子,利用自由面上的水平和垂向波动速度来表示自由面边界条件,推导了包含给定水流作用的新型Boussinesq型方程.截断到五阶导数项的一维理论模式,即

式中ηt为自由平面随时间变化的位移;为自由表面上速度势函数的水平梯度,为自由面上水平速度分量,为垂直速度分量;直角坐标(x,y,z)的原点在静水面上;z轴竖直向上为正;h为水深;η为自由面位移;µc为背景水流速度;g为重力加速度;和分别为任意水深z=处的水平速度分量和垂直速度分量;λ=h+=τh,其中 τ= −0.5,b1= −0.204113, b3=0.00653242.

涌浪运动是一种非均匀水流下的非线性运动,其变化是极其复杂的.由于涌浪的复杂性和随机性,观测方案、记录方式以及分析方法的选取和设计,都必须紧密结合谱的概念进行,利用谱进行海浪数值计算,是一种有效方法.可以通过其波高、周期和波长等参数,来反映涌浪运动的特性.

各种特征波高可用谱的相对于原点的0阶矩m0表示,波高的概率分布函数为[15]

式中

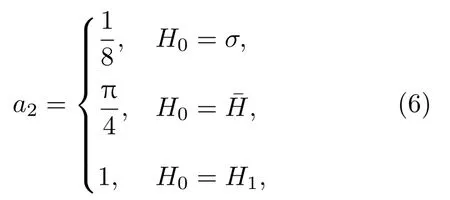
H0为特征波高,H1为均方根波高,为平均波高,取及α=1/8,σ为均方根方差,得2

由此得

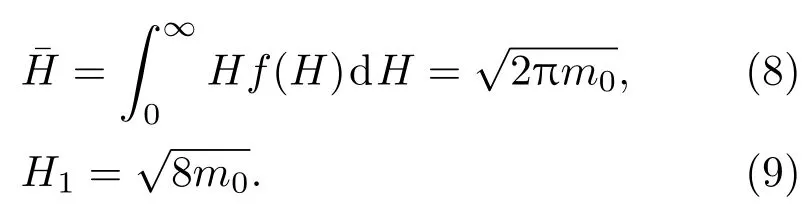
本文采用的是Pierson和Moscowitz[16]于1964年对于北大西洋的观测资料进行460次谱分析后,从中挑出充分成长的5个谱,依据风速10.3,12.9,15.5,18.0,20.5 m/s(特指海面上19.5 m高度处的风速),结果如图1所示.图1中S(ω)为无因次谱极值;f,ω分别为风浪的频率和角速度.由于海面上的风具有扰动性,以风要素对海浪进行无因次变化时,随着频率的增大,谱极值变化较明显,波能起伏较大.

图1 不同风速下充分成长有因次风浪频谱Fig.1.Frequency spectra of fully development Different wind and wave under Different wind speeds.

将不同形式的无因次谱进行拟合后,得到有因次的频谱为

式中无因次常数α=8.10×10−3,β=0.74;U为风速;ω=2π/T;ξ2为实测波面的方差.

应用以上公式计算波高时,可取m0等于ξ2,依据(10)式中的Pierson-Moscowitz谱[17]可得

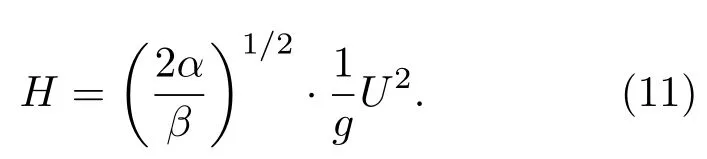
海浪传播的周期T可由已知的解析形式的谱进行计算,计算公式为[18]

式中B表示外部因素,如风要素或者波要素作为参量,对谱造成影响的一个系统.

对于(10)式中的Pierson-Moscowitz谱,B=βg4/U4时,由(12)式得

涌浪的波长计算公式为[18]

合并(13)式及(14)式得

在涌浪运动发生时,受风速变化的影响,随着风速逐渐增大,涌浪的波高和波长的变化趋势如图2和图3所示.

由图2和图3可见,随着风速的逐渐增强,涌浪的波长和波高逐渐增大,并且呈指数形式上升.

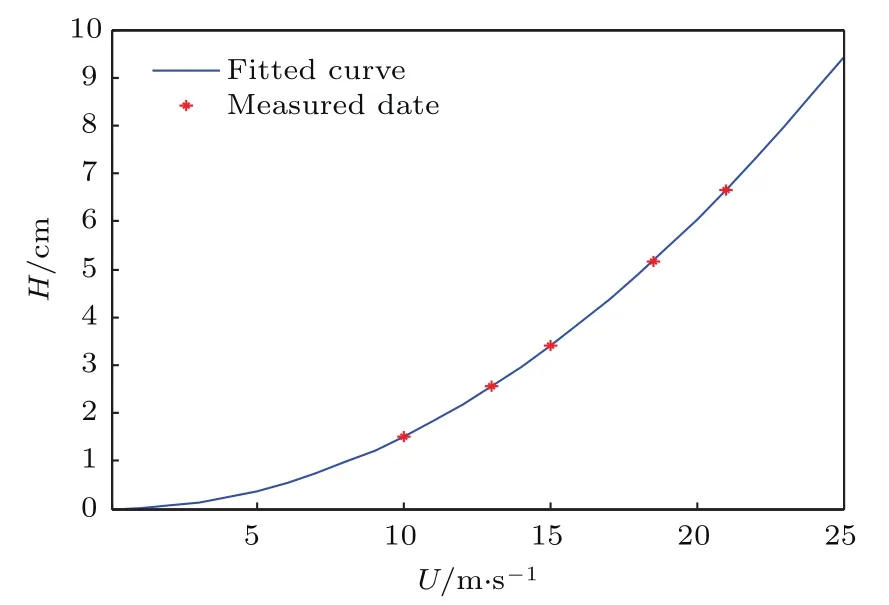
图2 不同风速下涌浪运动波高的变化Fig.2.Variation of wave height in wave motion under Different wind speeds.

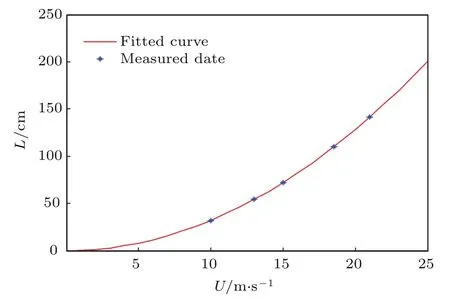
图3 不同风速下涌浪运动波长的变化Fig.3.Variation of wavelength in wave motion under Different wind speeds.

3 涌浪运动对水下量子信道纠缠度的影响

在涌浪运动的作用下,涌浪的波高以及周期的变化,会导致量子态相干性的破坏,这种现象称为量子消相干.消相干导致量子态所携带的信息丢失,量子纠缠度下降,从而影响量子通信.

根据文献[19],纠缠度可表示为

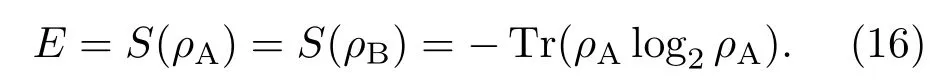
假设涌浪运动为系统A,量子信道为系统B,系统A的约化密度矩阵为

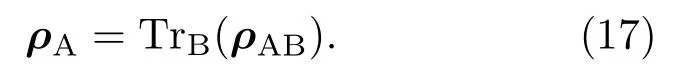
在进行水下量子通信时,两个系统相互作用形成的初始状态可表示为

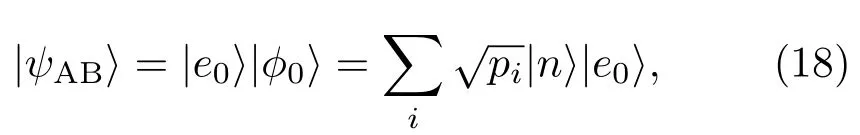
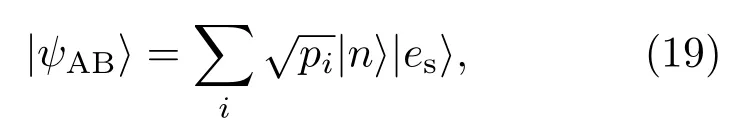
由(18)式和(19)式可知,量子信道纠缠度和涌浪运动的各项频谱特性有关,根据(11)式、(13)式和(14)式,定义在涌浪运动的条件下量子信道的纠缠度为

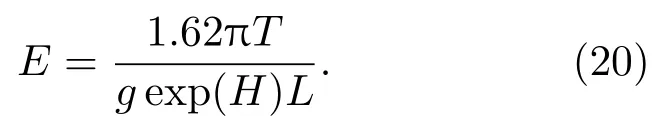
根据(20)式,量子信道的纠缠度与涌浪运动的波高、周期、波长有关.在海面风速为0—25 m/s时,涌浪的波长在0—200 cm变化,且海面风速为10.3,12.9,15.5,20.5 m/s时,对纠缠度E,涌浪传播的周期T及波高H的关系进行仿真,结果如图4所示.

由图4(a)—(d)可知,当风速在0—25 m/s变化时,随着传播周期的增大以及逆向水流的影响,量子信道的纠缠度增大,由0.0012逐渐增加到0.8426.另外,随着波动能量的增加,波高逐渐增大,海水对信号的衰减作用明显增强.

在不同风速下发生涌浪运动时,对纠缠度E,涌浪传播的周期T及波长L的关系进行列表分析,通过仿真,结果如表1和表2所列.由表1可知,周期在5.3—10.6 s时,纠缠度由0.2094上升到0.6775.由表2可知,波长在34.1—134.9 cm时,纠缠度由0.7093下降到0.2377.

表1 不同风速下纠缠度与周期的关系Table1.Relationship between the entanglement degree and the period under Different wind speeds.

表2 不同风速下纠缠度与波长的关系Table2.Relationship between the entanglement degree and wavelength under Different wind speeds.

由表1可知,周期的变化对纠缠度的影响较为明显,随着传播周期的增大,涌浪受逆向水流的影响,量子信道的纠缠度增大.由表2可知,随着波长的增加,波能传递的速率加快,波动能量增加,量子信道的纠缠度下降.

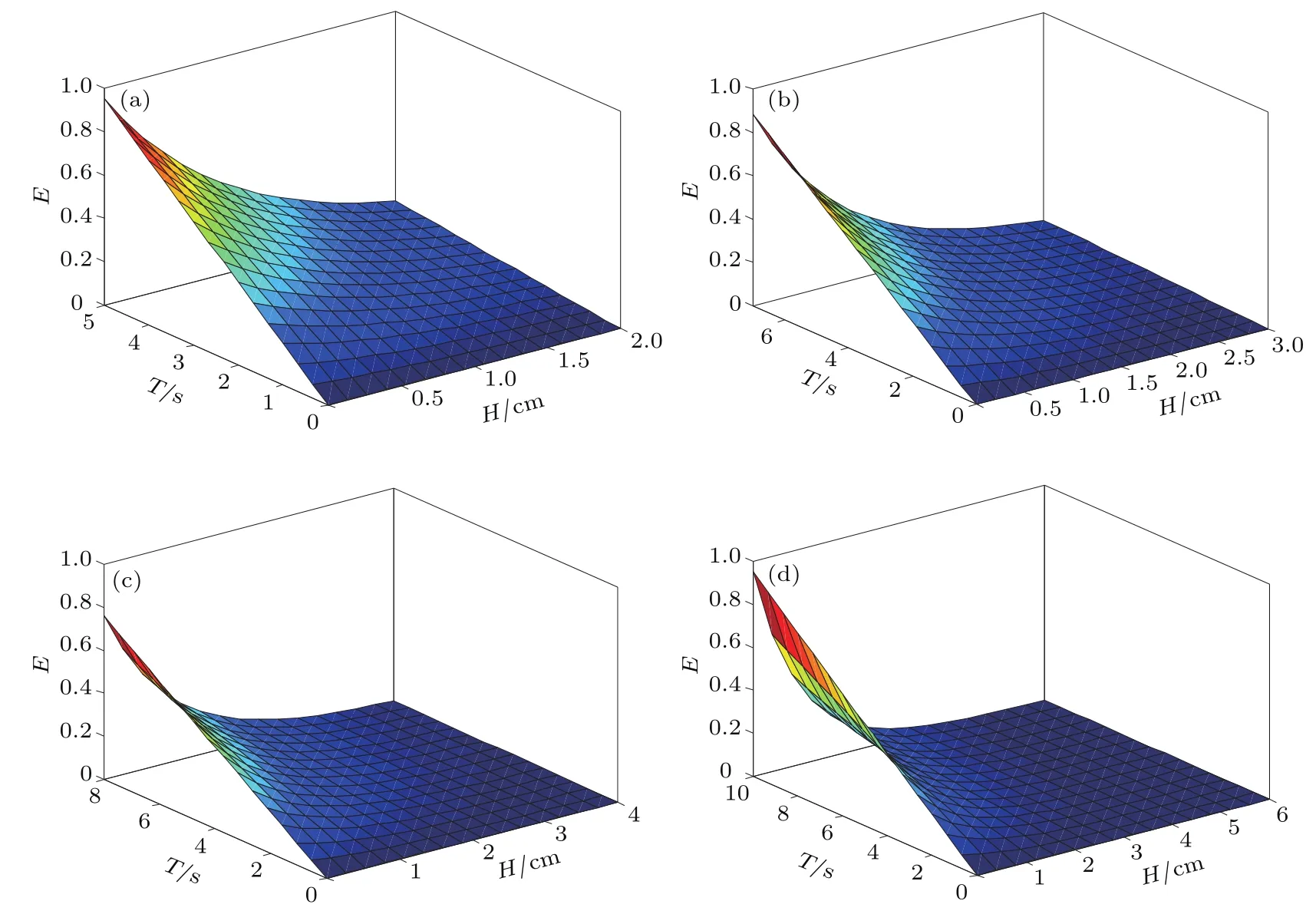
图4 不同风速下纠缠度与周期和波高的关系 (a)10.3 m/s;(b)12.9 m/s;(c)15.5 m/s;(d)20.5 m/sFig.4.Relationship of the entanglement degree with the period and with the wave height at Different wind speeds:(a)10.3 m/s;(b)12.9 m/s;(c)15.5 m/s;(d)20.5 m/s.

4 涌浪运动对系统中量子信道容量的影响

涌浪运动会对量子态相干性造成破坏,量子信道噪声会引起信道容量的变化.下面以退极化信道为例,建立涌浪物理特性与退极化信道容量的关系.

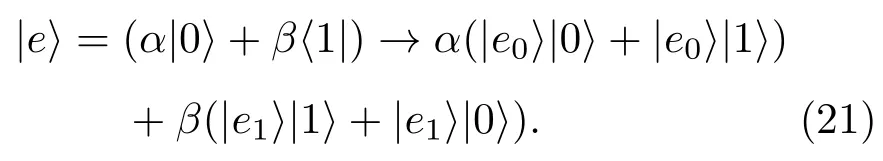
将涌浪运动态表示为

式中m为量子位的退极化概率.

退极化信道可表示为[21]

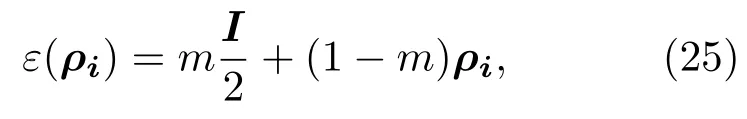
式中ρi为量子比特,m为量子位的退极化的概率;I/2为完全混合态,ε(ρi)为量子系统经过退极化信道后的状态.

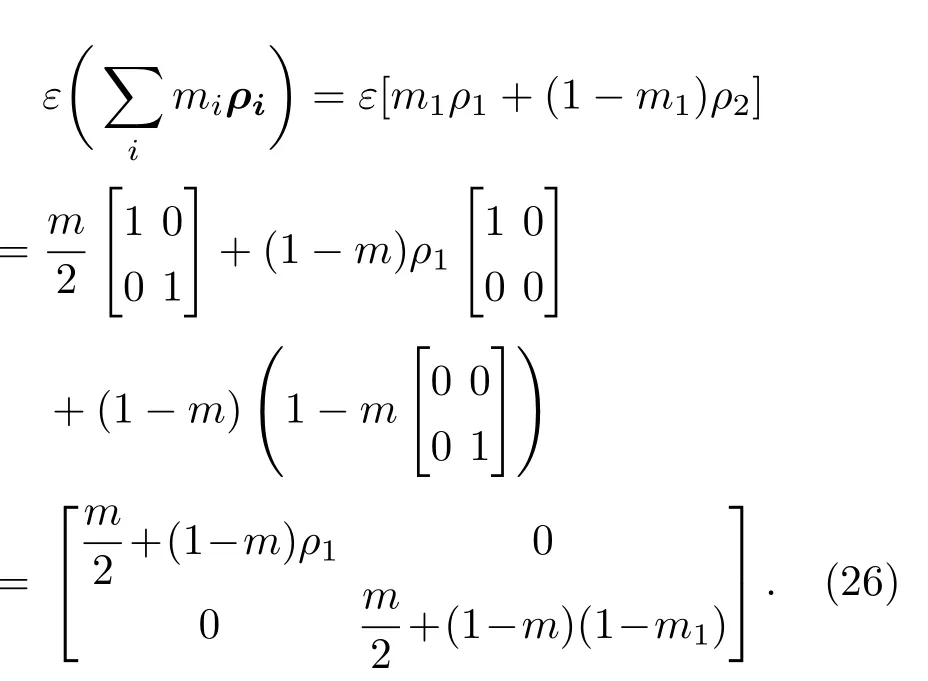
对应的诺依曼熵为

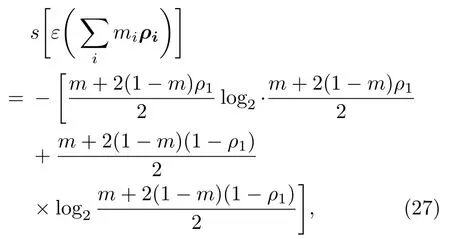
输出的诺依曼熵为

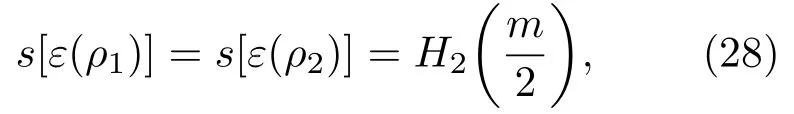
由此,信道容量为

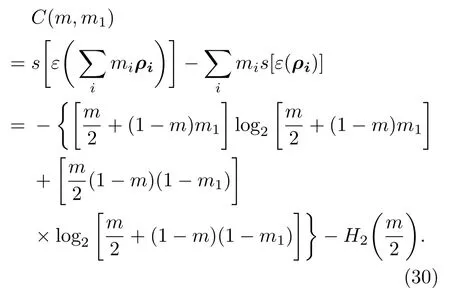
因此信道容量为

在涌浪运动的条件下,根据涌浪波高和周期联合分布的概率密度函数及海浪频谱的无因次常数与平均波长的关系[22−23],涌浪运动条件下量子位的退极化概率为

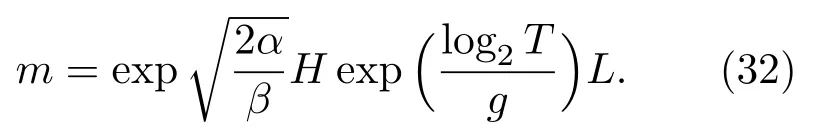
对量子信道容量、涌浪的波高及传播周期之间的的关系进行仿真,结果如图5所示.

图5 信道容量与波高和周期的关系Fig.5.Relationship between channel capacity and wave height and cycle.

由图5可知,涌浪运动在风速变化的影响下,涌浪传播周期增大,受逆向水流的影响,量子信道容量逐渐减小.随着波动能量的增加,波长逐渐增大,波能传递的速率加快,造成信道容量逐渐降低.

对量子信道容量、涌浪的波长及传播周期之间的的关系进行仿真,结果如图6所示.

图6 信道容量与波长和周期之间的关系Fig.6.Relationship of the channel capacity with the wavelength and with the cycle.

由图6可知,当风速在0—25 m/s变化时,在涌浪运动的绕射作用下,随着波长的增加,波能传递的速率加快,波动能量增强,量子信道容量下降,在波长较大的情况下,周期的变化使得信道容量下降的趋势更加明显.随着传播周期的增大,涌浪受逆向水流的影响,量子信道容量减小,由0.8736减小到0.1024.

5 涌浪运动对量子密钥分发过程中误码率的影响

基于BB84协议下的量子密钥分发系统,量子误码率NQBER为接收到的误码比特率Nerror与总比特率Rsift之比,是对系统评估的有效参数[24],即

式中χ为光电探测量子效率;ηa= ηB/2+ηD,ηB为背景噪声引起的光子计数,ηD为光电探测器的暗电流计数;δ为退极化效应因子;FS为筛选因子;Rr为发射脉冲重复率;Fc为测量因子;κ为激光脉冲平均光子数;Ta为系统传输率;P为单光子俘获率;信道传输因子Tc为

式中K/K0为传输振幅比,K为量子态传播后的振幅,K0为初始振幅;为高斯光束远场发射角;Aatm为链路衰减系数.

表3 信道误码率的各项参数取值Table3.Parameter values of channel error rate.

由图7可知,当波长和波高同时在0—2 cm增加时,误码率呈指数形式增加,由0.1651增加到0.4812.由此可知,在进行水下量子通信时,量子态在传输过程中,受涌浪运动作用的影响,量子密钥分发过程受到干扰,影响系统的通信性能.

图7 误码率与波长和波高的关系Fig.7. Relationship of the bit error rate with the wavelength and with the wave height.

6 结 论

本文研究了非均匀水流中涌浪运动对水下量子通信性能的影响.根据涌浪运动传播的特性,建立了量子信道的纠缠度、信道容量以及密钥分发中误码率与涌浪运动特性之间的函数关系,分析了其频谱特性,这对水下量子通信研究有一定重要意义.仿真结果表明,随着涌浪运动波长和波高的增大,量子信道纠缠度和信道容量近似呈指数减小.涌浪传播周期和波长越大,量子密钥分发过程中误码率越高.因此,在进行水下量子通信时,涌浪运动会对通信系统造成一定的影响,可根据气象条件,自适应调衡系统参数,降低涌浪对量子通信的影响.