一种基于文本互信息的金融复杂网络模型∗

孙延风 王朝勇

1)(吉林大学计算机科学与技术学院,长春 130012)2)(吉林工程技术师范学院信息工程学院,长春 130021)

(2017年11月21日收到;2018年3月22日收到修改稿)

复杂网络能够解决许多金融问题,能够发现金融市场的拓扑结构特征,反映不同金融主体之间的相互依赖关系.相关性度量在金融复杂网络构建中至关重要.通过将多元金融时间序列符号化,借鉴文本特征提取以及信息论的方法,定义了一种基于文本互信息的相关系数.为检验方法的有效性,分别构建了基于不同相关系数（Pearson和文本互信息）和不同网络缩减方法（阈值和最小生成树）的4个金融复杂网络模型.在阈值网络中提出了使用分位数来确定阈值的方法,将相关系数6等分,取第4部分的中点作为阈值,此时基于Pearson和文本互信息的阈值模型将会有相近的边数,有利于这两种模型的对比.数据使用了沪深两地证券市场地区指数收盘价,时间从2006年1月4日至2016年12月30日,共计2673个交易日.从网络节点相关性看,基于文本互信息的方法能够体现出大约20%的非线性相关关系;在网络整体拓扑指标上,本文计算了4种指标,结果显示能够使所保留的节点联系更为紧密,有效提高保留节点的重要性以及挖掘出更好的社区结构;最后,计算了阈值网络的动态指标,将数据按年分别构建网络,缩减方法只用了阈值方法,结果显示本文提出的方法在小世界动态和网络度中心性等指标上能够成功捕捉到样本区间内存在的两次异常波动.此外,本文构建的地区金融网络具有服从幂律分布、动态稳定性、一些经济欠发达地区在金融地区网络中占据重要地位等特性.

1 引 言

统计物理方法有助于从系统复杂性的角度理解社会和经济问题[1],解释复杂系统随时间演化的过程.金融物理学(econophysics)则运用统计物理方法来研究金融复杂系统中各个领域的相关问题[2−4].由于受到政治、战争、宏观经济以及社会舆论等多种因素的影响,至今没有一个完美的理论能完全揭示出金融系统整体的运行规律.现今金融系统中的很多研究都是基于各种假说,比如套利定价理论(arbitrage pricing theory,APT),有效市场假说(efficient markets hypothesis,EMH)[5,6]等.借助于复杂网络建模思想,可以在较少市场假说下,实现对整个金融系统中各种变量相互关系的研究,能够从整体上研究金融主体之间的相互依赖性,反映金融市场整体的拓扑结构[7].

许多金融市场问题都可以使用复杂网络方法建模,常见的有股票市场[8−14]、外汇市场[15−17]、银行信贷关系[18]、信用卡市场[19]、期货市场[20,21]以及房地产市场[22−24]等.数据上使用较多的是低频数据(主要是每日数据),也有些研究使用了高频数据[17,25−27].金融复杂网络模型主要有最小生成树(minimal spanning trees,MST)[14−16]、最大生成树(maximal spanning trees)[28]、平面极大过滤图(planar maximally filtered graph,PMFG)[24]、阈值网络(threshold networks,TN)[11,29,30]、随机矩阵理论(random matrix theory,RMT)[8,23,31]、差分网络(differitial network)等[32].通过选择不同的网络节点、不同的数据类型、不同边的连接方式(有向[17]或无向)构造出不同的金融复杂网络模型,研究各种金融拓扑结构、计算金融风险统计特征,用来解决不同的金融问题,构建金融投资组合以及度量金融系统风险大小[15]等.

金融复杂网络建模中一个重要的步骤是计算节点之间的相关矩阵.一种方法是使用Pearson相关系数.Mantegna[9]在1999年将其用于美国股票市场,并构造了一个MST网络.此后Pearson相关系数被广泛应用于金融复杂网络中,Wang和Xie[24]使用Pearson相关系数构造了20个国家不动产证券市场的三个网络模型,即MST,HT和PMFG;Wang等[14]则将Pearson相关系数用于57个股票市场动态网络的构建.Pearson相关系数是一种线性相关系数,然而金融系统具有典型的非线性特征,为此一些学者在计算相关矩阵时使用节点间的互信息(mutual information,MI)来度量节点之间的相关性[15,17,33].互信息以信息论[34]为基础,能够度量两个不同序列之间包含多少相同的信息,反映两个变量序列之间的非线性相关关系,因此在金融复杂网络中得到了广泛应用,并在此基础上发展了很多其他度量非线性相关的方法,比如互信息率(mutual information rate,MIR)[33]、偏互信息(partial mutual information,PMI)[30,35]等.

Fiedor[33]引入互信息和互信息率作为相似性度量指标,用来替代Pearson相关系数,使用Lempel-Ziv复杂度[36]来估计MI和MIR.网络缩减模型采用的是MST和PMFG模型,并应用于纽约证券交易所100指数(NYSE100)的91家企业在2003—2013年的日收盘数据.为检验替换效果,采用了平均最短路径(average shortest path,ASP)等指标,从节点、聚类以及网络等三个层面与Pearson相关性进行了对比.结果显示MI具有比Pearson相关性更优秀的特征,但MIR效果差一些.You等[35]对上海股票市场的复杂网络的非线性相关问题进行了讨论,使用PMI度量节点间的相关性,并与Pearson相关性做了对比.假定样本服从Dirichlet分布,使用熵(entropy)的Schurmann-Grassberger来估计PMI,分别采用MST和PMSG模型为网络缩减方法.使用Pearson相关性、MI和PMI作为相关性度量方法,得到6组不同的网络.从相关性、经济部门结构、节点度分布以及网络中重要程度不同的股票(从节点度大小的角度度量)在经济上每股收益率的变化等方面进行了对比研究.Fiedor和Holda[15]将MI用于外汇市场,使用Lempel-Ziv算法估计MI,采用了MST和PMFG模型,分析了汇率之间的非线性相互依存关系.认为根据熵率的不同,不同汇率变化的可预测性是不同的,因此汇率投资组合中不但要考察VaR等风险指标,还要考察可预测性.此外,可以通过复杂网络中节点的远近直接观察出两种货币之间的相关性(或互信息)的大小关系,相关性越低则风险越小,越适合作为投资组合的组成部分.与其他在一维空间使用Lempel-Ziv复杂度的文献不同,Fiedor[13]为计算互信息率,将Lempel-Ziv复杂度扩展到多维信号,来研究不同金融工具序列之间的高阶相关性,然后将其转换成欧几里德度量,采用MST和PMFG模型,以便找到网络建模金融市场的合适的拓扑结构.结果表明这种方法会导致与大多数研究中使用基于相关的方法不同的结果.

参考文献[33,35]在计算互信息时假定样本服从Dirichlet分布,并且需要将样本离散成几个不同的状态(比如人为分成4个部分或8个部分[33]).本文借鉴文本特征提取的互信息方法以及时间序列符号化方法,构造一个简单的非线性相关性度量方法,该方法不再假定样本服从Dirichlet分布,也不进行人为的离散化.为检验该方法的效果,将其用于中国沪深两地证券市场的地区指数收盘价数据集,建立地区金融网络模型,分别进行静态与动态分析,考察所建立模型的拓扑性质.

本文安排如下:第2节完整叙述本文的模型,建立4个不同的地区金融网络模型;第3节介绍使用的数据来源、数据前期处理以及数据相关的统计特征以及地区金融网络拓扑特征等;第4节从节点相关性、网络拓扑指标、度分布的幂律检验以及动态网络拓扑指标等多个不同的角度对本文提出的方法进行数值检验,并与Pearson相关系数对比;第5节进行概括性的总结与展望.

2 地区金融网络模型

本节在金融时间序列符号化基础上,使用改造的文本互信息方法计算相关系数,随后建立4个金融复杂网络模型.这些模型的相同点是节点都是地区指数,节点间的相互链接都用相关性表示,相邻边的权值都用相关系数的大小表示;不同之处在于使用的网络精简方法以及获得相关系数的方法不同.

2.1 基于文本互信息的相关系数

互信息在文本特征选择中有广泛的应用[37],互信息能够度量两个随机变量的相互依赖性.如果设文本特征项为t,类别为TC,则它们之间的互信息可定义为

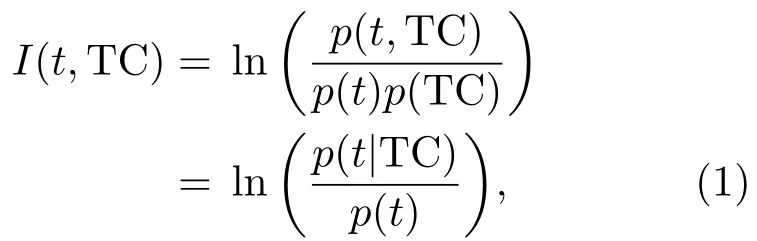
其中p(t,TC)为文本特征项t和类别TC的联合分布,p(t)和p(TC)分别是特征项t和类别TC的边际分布.本文将文本互信息公式改造后应用到两个金融时间序列的相关性度量中.

为此需要将时间序列符号化,进一步可以估计出符号序列的统计信息,计算出两个序列之间互信息的大小.符号化的处理方法在很多金融复杂网络相关文献中被广泛使用,并已取得了良好的效果[38,39].对于一个金融时间序列,可以利用(2)式将其符号化,

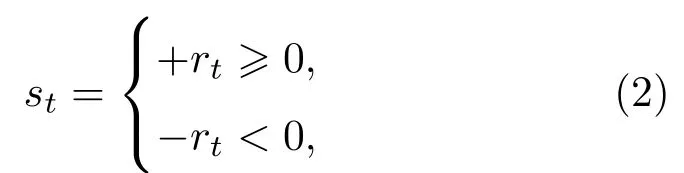
其中 st为第t天符号化序列,rt为第t天地区指数收盘价的对数收益率.

对于两个金融时间序列X,Y,在给定的第t天,可以定义4种模式,它们分别是:{+,+}{−,−}{+,−}{−,+},统计这4种模式在给定区间内的总数,分别记为A,B,C,D.则可利用(3)式计算这两个金融时间序列在给定区间内的互信息相关性:

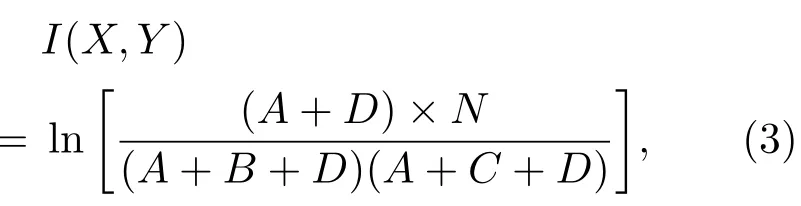
其中N=A+B+C+D.

由(3)式可见,两个序列的互信息是完全对称的,即I(X,Y)=I(Y,X);互信息越大,两个序列同涨同跌的可能性越大,两个序列的相关程度也越大;当两个序列完全相关时,B=C=0,N=A+D,则I=1;两个序列完全无关时p(t,TC)=p(t)p(TC),A+D=0则I=0.

但(3)式定义的互信息相关系数不能满足距离的3个条件.本文采用很多金融复杂网络文献普遍使用的方法[9]将其转化为距离:

此时0 6 d 6 2,并且满足距离的3个条件.

2.2 4个地区金融网络模型

为考察MI相关系数在构建地区金融网络方面的优势,将其与使用Pearson相关系数的相同金融网络从相关性分析、网络拓扑指标数值大小、度的幂律分布以及动态网络特性等几个方面进行了比较.

使用不同的相关系数(线性的Pearson方法,非线性的MI方法)和网络精简方式(TN和MST)构建4个金融地区指数的复杂网络,见表1.这4个地区金融网络模型都是无向的、加权的复杂网络.

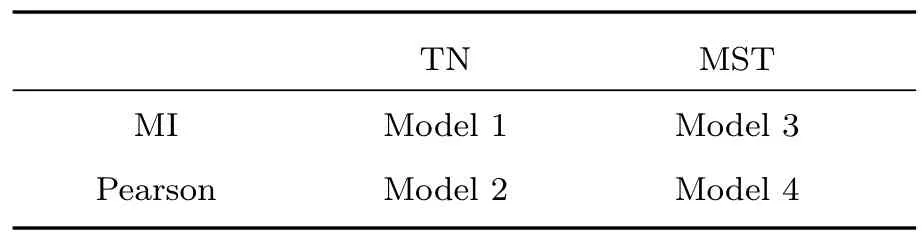
表1 不同相关系数和精简方式构建的模型Table1.Models created with Different correlation coefficient and Different simplified method.

3 检验数据

为检验4个地区金融网络模型,使用中国沪深两地证券市场的真实数据.数据采集于深圳市财富趋势科技股份有限公司的通达信Windows版软件[40]中的地区指数收盘价,共32个地区(不包括港澳台,深圳单独算一个地区),时间区间从2006年1月4日到2016年12月30日,共计2673个交易日.

采用这组数据的优势在于:1)每个地区都涵盖了本地区沪深上市公司的A股、创业板、中小板等板块,这些地区指数基本上代表了沪深两地全部的上市公司,能够较全面地刻画中国沪深证券市场的情况,反映证券市场整体的运行信息;2)这些地区指数在所选时间段内几乎没有因停牌等原因造成的数据缺失或异常(除了贵州板块指数数据在2006年5月19日至2006年5月24日数据异常,处理方法是将此区间内数据全部使用前一日即2006年5月18日的数据代替),不需要对数据进行人为的删除或更新;3)与其他文献不同的是,本文把证券市场按地区划分,并从复杂网络的角度研究证券市场的地区性质,从而得出一些关于地区板块指数的结论.

为消除个别数据异常波动造成的影响,使数据更加平稳,采用沪深股票市场地区板块指数的对数收益率,

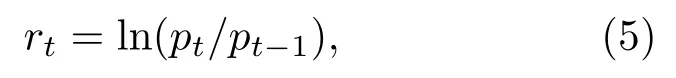
其中rt为第t天的日对数收益率;pt为地区板块指数在第t天的日收盘价.

网络的精简方式分别使用TN和MST,这两种方法都能够过滤掉一些次要信息,便于对金融网络中最重要的信息进行分析,有助于理解金融市场的动态拓扑特征.

MST在最大程度上对网络精简,只研究金融网络中最相关的依赖关系,降低了金融网络模型的复杂度,更有利于大型网络分析,对于金融市场的海量数据来说有重要意义.

在构建TN时,一项重要的工作是选择阈值,通常的做法是人为给定阈值,也有学者使用均值和方差来确定阈值,或者绘制经验密度函数[11,41].本文采用分位数的方法确定阈值:将相关系数(变成距离d并去掉0后)在其最小值和最大值的区间内若干等分,然后取其中一个区间的中点为阈值.经过对地区指数数据的不同时间段与不同相关系数的反复测算,发现将数据6等分并取第4个区间的中点为阈值较为合理,大约能够涵盖25%的数据值,这比Brida和Risso[41]建议覆盖50%的累积分布值略少.这样选择的阈值,能够使得所保留的边数适中,保留较为重要的节点连接和便于观察的网络拓扑结构,得到相应的统计指标,更为重要的是能够使得MI和Pearson方法得到的连边数最为接近,便于两种方法的对比.

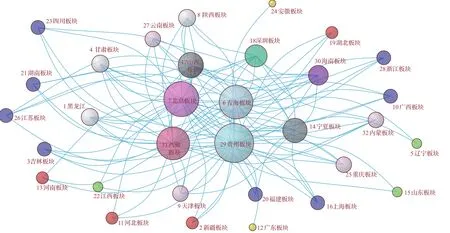
图1 Model 1的网络拓扑图(阈值为0.91)Fig.1.Network topology of Model1(threshold is 0.91).

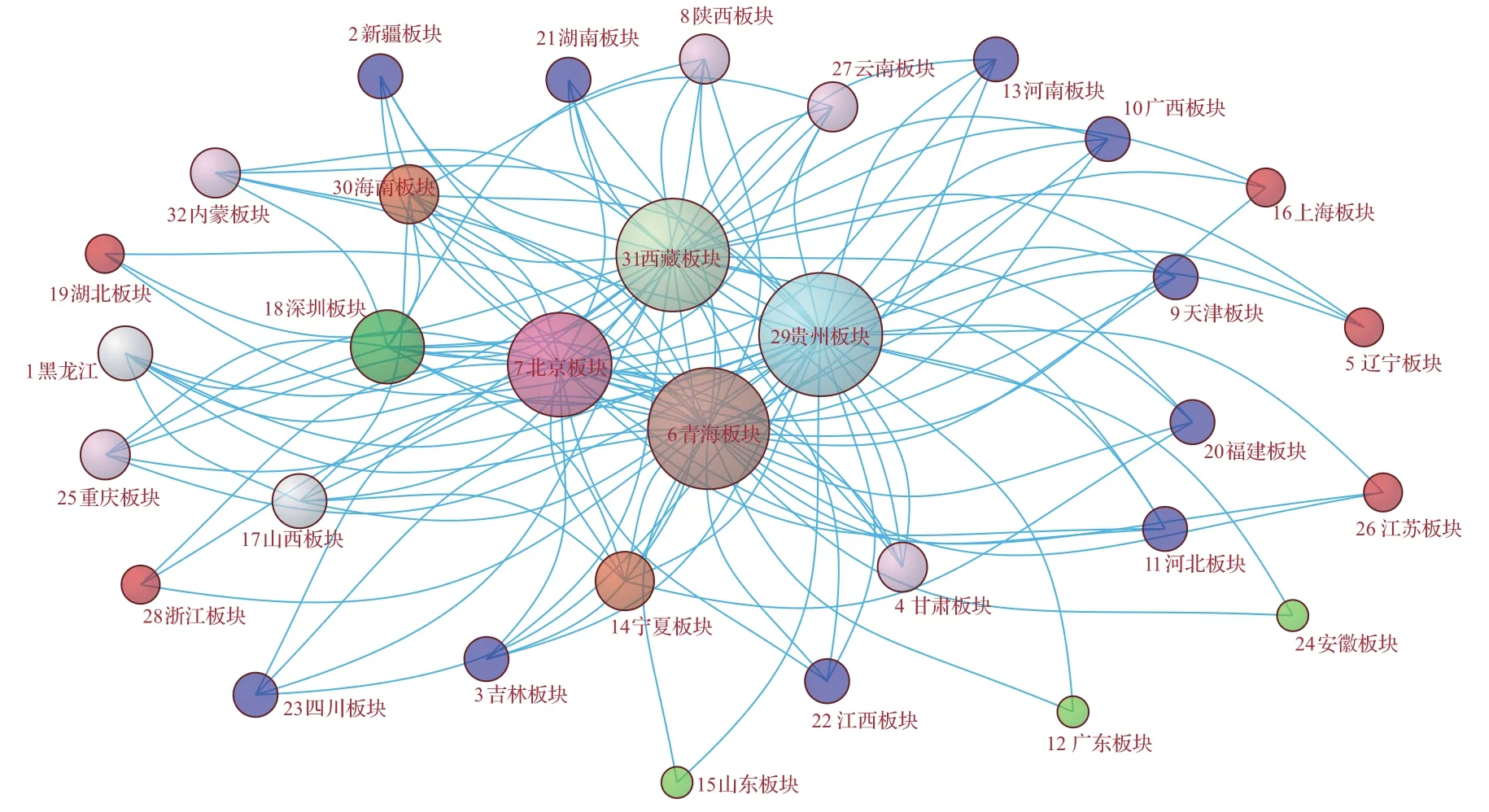
图2 Model 2的网络拓扑图(阈值为0.61)Fig.2.Network topology of Model 2(threshold is 0.61).

图1—图4给出了4种网络模型Model 1—Model 4在整个数据区间的网络拓扑图.从4个模型的网络拓扑图可以看出,度值大的结点在网络中占较少的部分,但对金融网络中的多数节点都有较大影响.

在Model 1和Model 2中,阈值的确定采用上面提出的分位数方法,此时两个模型的连边数分别为117和116条,较为接近,便于对比两种方法的拓扑结构与拓扑指标.

对于TN网络(图1和图2),MI和Pearson方法在节点度上大于21的节点共有4个,并且这4个节点完全相同,只是在北京板块和西藏板块的节点度上有所不同:北京板块的度值在MI中为25,在Pearson中为22;西藏板块在MI中为22,而Pearson中为26.MI方法提高了北京板块的度,降低了西藏板块的度,本文认为这种改变应该更合理一些.在MST网络中(图3和图4),两种相关系数模型中,度大于6的节点共有3个,黑龙江(度值为7)和辽宁(度值为7)板块相同,度的大小也相近.另外的节点在Model 3中为湖北板块(度值为7),而Model 4中为山东板块(度值为9),存在一些差异.

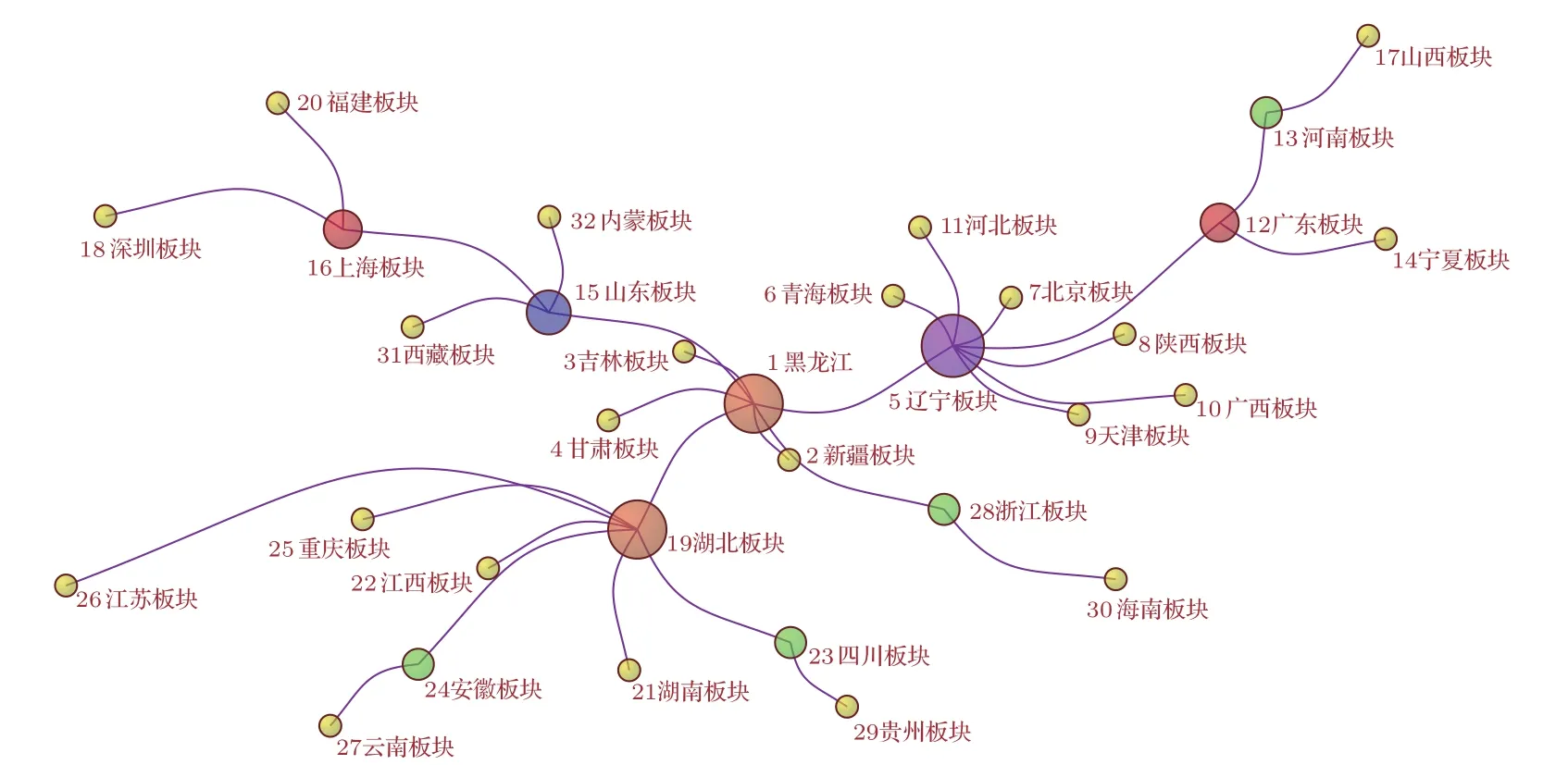
图3 Model 3的网络拓扑图Fig.3.Network topology of Model 3.

图4 Model 4的网络拓扑图Fig.4.Network topology of Model 4.

在以地区指数为节点的4个金融复杂网络模型中,从度的大小看,西藏、贵州、青海等西部板块以及黑龙江、辽宁等东北板块占据了重要的地位,说明在中国的股票市场中,经济欠发达地区的股票有重要的地位,这一点在后面逐年的复杂网络中得到了进一步的证实.分析其中的原因发现,这些地区中有如600519贵州茅台、600338西藏珠峰、600117西宁特钢等活跃度较高的上市公司,因此从证券投资的角度看,重视这些地区的上市公司的投资将会对收益产生一定的影响.

由上文的分析可以看出，1974年和1992年的公约对波罗的海沿岸国如何携手共同对抗波罗的海海洋污染所涉及的方方面面做出了细致、清晰、周全的规定和安排，加上公约设立赫尔辛基委员会、重视科学技术成果的引入、灵活利用区域和国际组织、不断自我更新的特色，开启了波罗的海沿岸国在海洋环境保护领域的正式合作，为持续数十年并取得积极进展的波罗的海环保实践，提供了极为关键的框架性法律保障。

为反映中国股票市场整体状况,考察上述数据区间对应的上证综指收盘价,因为其能够代表整个市场的运行状态.这期间(即从2006年1月4日—2016年12月30日)包含了2次较大的波动:2007年10月16日附近(最高6092.06点)以及2015年6月12日附近(最高5166.35点).接下来在4.4节动态网络逐年对比分析中将重点考察不同模型对这两次大幅波动的捕捉能力.

4 结果分析

使用上节的地区板块指数数据以及第2节建立的4个地区金融网络模型(Model 1—–Model 4),本节从节点的相关性分析、网络整体拓扑指标、度的幂律分布检测以及动态网络拓扑特征(这里只讨论TN网络)4个方面分别讨论以MI与Pearson为相关系数的地区金融网络的优缺点.

4.1 节点相关性分析

为对比使用MI与Pearson相关系数的不同效果,首先计算4个地区金融网络模型中每个节点的接近度(closeness)中心性,介值(betweenness)中心性,平均最短路径长度(average shortest path length,ASPL),特征中心性(eigencen)等4个指标;然后计算TN网络即Model 1和Model 2的节点序列在上述4个指标上的相关度,结果见表2第1行;最后计算MST网络即Model 3和Model 4的节点序列在上述4个指标上的相关度,结果见表2第2行.

从表2可见,除了MST(Model 3与Model 4)的ASPL相关度为0.4358,其他都在0.76—–0.94之间,这说明本文提出的文本互信息方法大约体现了20%左右的非线性相关关系.与You等[35]的结果很相近,而与Fiedor[33]的30%相比少了一些(文献[33]的结果中也存在0.8以上的相关度).产生这种现象的原因我们认为与数据有关,You等[35]使用的数据是上交所上市公司的数据,与本文的数据源很相近,而Fiedor[33]使用的数据是相对成熟的市场,即纽交所(New York Stock Exchange)的数据.

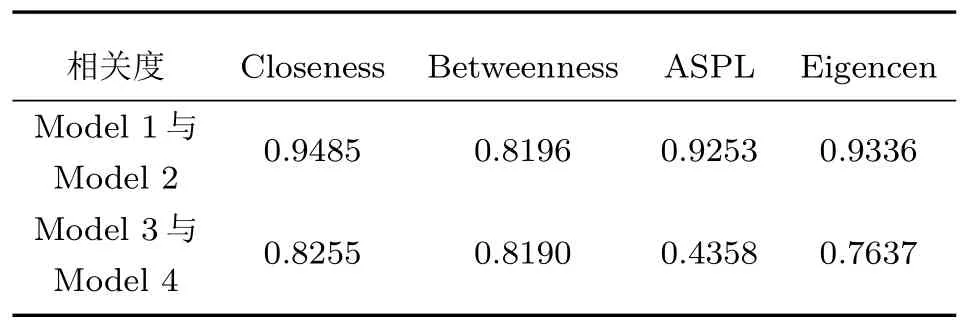
表2 节点相关性分析Table2.Correlation analysis for nodes.

4.2 网络拓扑指标

本小节从网络的层面对4个模型的拓扑指标进行对比.分别计算不同网络的平均加权度、介值中心性、网络聚类系数以及模块度等,计算结果见表3.

表3 MI和Pearson相关系数的指标Table3.The index of MI and Pearson correlation coefficient.

平均加权度(average weighted degree,AWD)是一种度量网络中节点的平均重要程度的指标,考虑了每个边权重大小的不同,计算时将边的权重求和,然后除以节点数.不论TN(Model 1)还是MST(Model 3)网络,使用MI相关系数所保留的节点的平均加权度均高于Pearson相关系数,体现了MI相关系数在保留重要节点上优于Pearson相关系数.

网络介值中心性(network betweenness centralization,NBC)为金融网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例,是衡量网络节点作为桥梁中介程度的指标,介值数高的节点(地区指数)在金融网络信息传输中起着至关重要的作用.从表3可见,MST中MI(Model 3)和Pearson(Model 4)的NBC值都是0.7左右,但TN中,MI(Model 1)的值要比Pearson(Model 2)的值高出30%左右,说明对于TN网络而言,MI能够有效提高所保留节点的介值重要性.

聚类系数体现了节点的集聚程度.在Pajek软件[42]中有加权和不加权两种:网络的 Watts-Strogatz聚类系数(Watts-Strogatz clustering coefficient,WSCC)是所有节点的聚类系数的非加权平均;网络集聚系数(network clustering coefficient,NCC)是所有节点的聚类系数的加权平均.从表3可见,在TN网络中(Model 1和Model 2),地区指数的WSCC都为0.84左右,而NCC分别为0.36和0.296,数值较大,说明我国上市公司地区指数网络的集聚程度较高,具有小世界网络的集聚特征.从三角节点数量上看,在使用的边差不多的情况下,MI(Model 1)提取出的三角数量比Pearson(Model 2)多出20多个,说明MI能够提高节点的质量.

从模块化程度上看,模块度(modularity)能测量社区划分的质量,是一种衡量网络社区结构强度的方法.本文采用了Blondel等[43]的算法计算模块度,参数为默认的(随机,使用边的权值,Resolution取1).在MST网络中模块度均大于0.6,划分质量较好,描述了网络中强大的社区结构和明确的社区划分[44];而TN网络的模块度均小于0.1,划分质量差一些.从数量上看,不论是MST网络还是TN网络,MI均大于Pearson,这一点在TN网络中尤其明显,说明MI方法更能挖掘出更好的社区结构.此外,从社区结构的数量(number of communities,NOC)看,在相同的情况下,MI方法(Model 1和Model 3)均略少于Pearson方法(Model 2和Model 4),说明MI方法保留的节点关系更为密切,联系更为紧密.

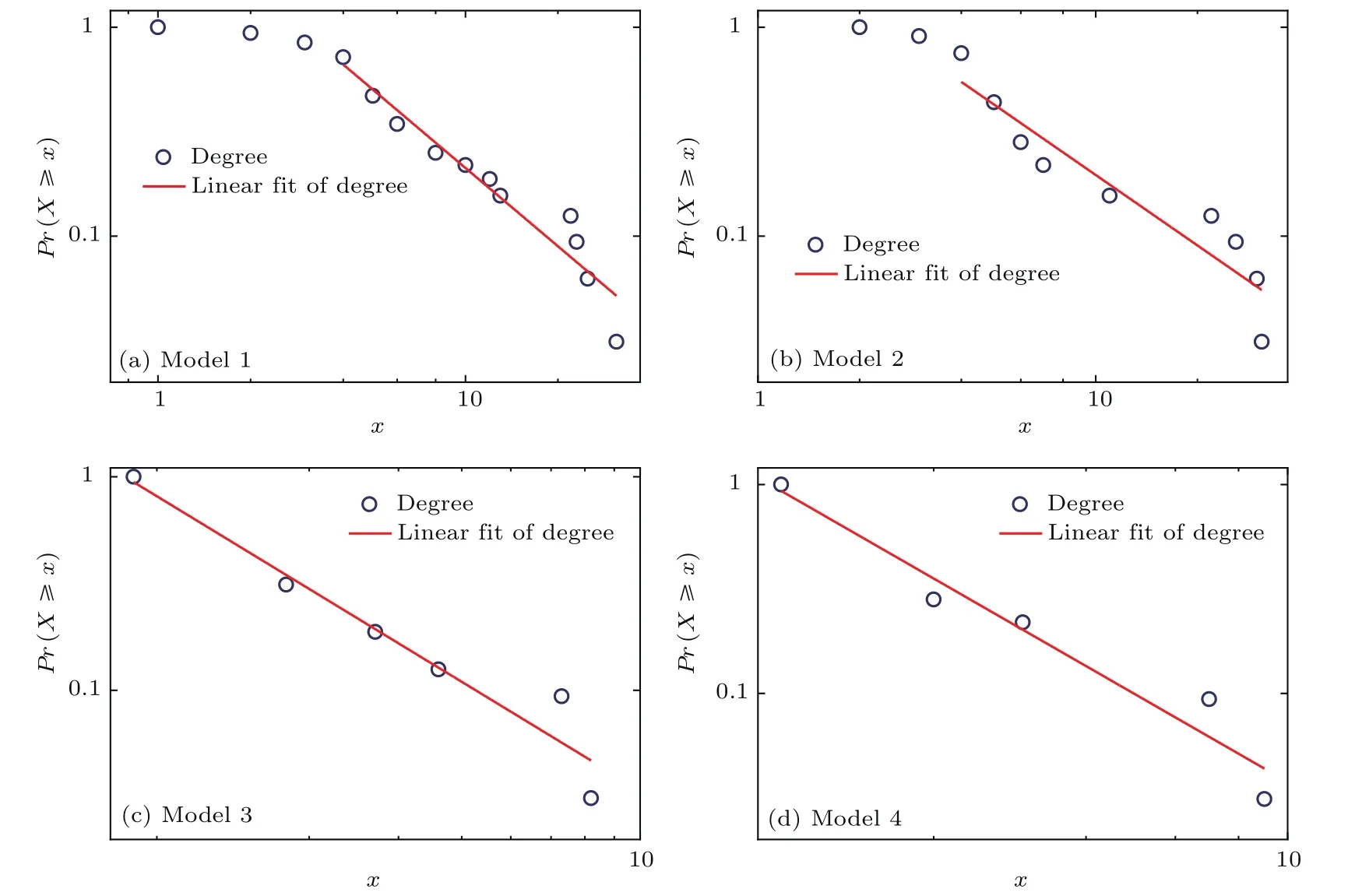
图5 双对数坐标下度分布及线性拟合图Fig.5.Degree distribution in LogLog and their linear fitting.

4.3 度的幂律分布

对于给定的数据和网络结构,每个节点的度都是固定的.本节使用Clauset等[45]的方法来考察节点度的分布情况.

Model 1—Model 4这4种网络的双对数坐标下的节点度分布以及相应的线性拟合见图5,从图中可以看出明显的幂律分布特征.

4.4 动态指标对比

与前面几节中使用整个数据集构建网络不同的是,本节将数据按年度划分,分别构建11个网络.由于MST网络过于精简,本小节将只考虑TN网络,分别使用MI和Pearson为相关系数,分别对11个年份数据构造金融网络,阈值均采用上面提到的分位数统计方法,主要考虑MI和Pearson两种方法的可对比性(连边数最为接近).分别从小世界动态指标、网络度中心性以及Jaccard指标等3组动态指标上考察捕捉2007年和2015年上证综指两次大幅波动的能力.

小世界动态指标(dynamics of the smallworld)定义为网络平均最短路径长度与网络聚类系数之间的比值[46].图6中MI(实线)小世界动态指标的值在2015年达到极值,并且在2007年也出现了一个局部峰值.与其对比的是图6中Pearson(虚线)小世界动态指标峰值出现在2012年,2015年次之.这两个图的对比说明对于异常年份的反应能力MI比Pearson有所提高.

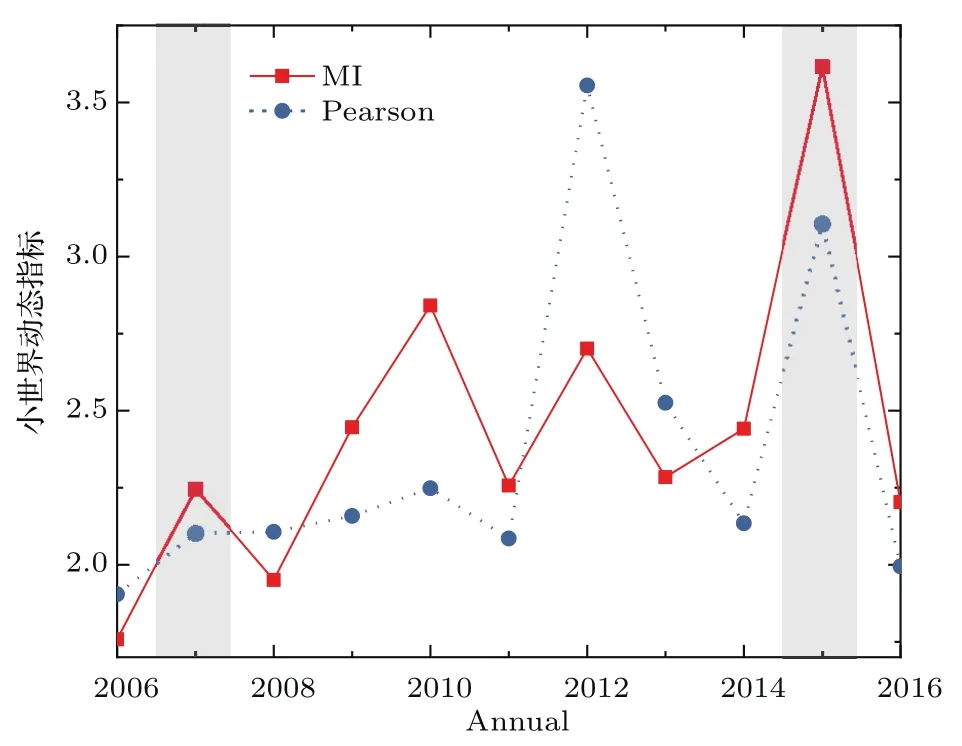
图6 TN网络的小世界动态指标Fig.6.Dynamics of the small-world of TN.

逐年的网络度中心性(network degree centralization)指标如图7所示,可以看出,MI(实线)在2015年达到次高峰值,2007年也出现了局部峰值;而Pearson(虚线)则在2007年没有出现峰值.此外,考察每年节点度的大小,MI和Pearson两种方法中,贵州板块除了2015年度较小外(MI为13,Pearson为15),其他年度均具有较大的度值(30左右),说明近些年贵州板块发挥了重要的作用.

Jaccard指标[47]能够识别动态TN的稳定性,2个阈值网络之间的Jaccard指标定义为[29]

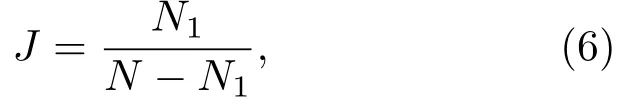
其中N1是两个阈值网络间相同节点对的连接数目;N是这两个阈值网络总的连接数目.

Jaccard指标计算结果如图8所示,MI(实线)的平均值为0.397(2012—2013年间的最小值为0.292,这段时间上证综指波动幅度较小).Pearson(虚线)的平均值为0.519.从Jaccard指标看,MI和Pearson模型的Jaccard值多数都在0.3以上[29],说明地区指数数据具有网络的动态稳定性[47].

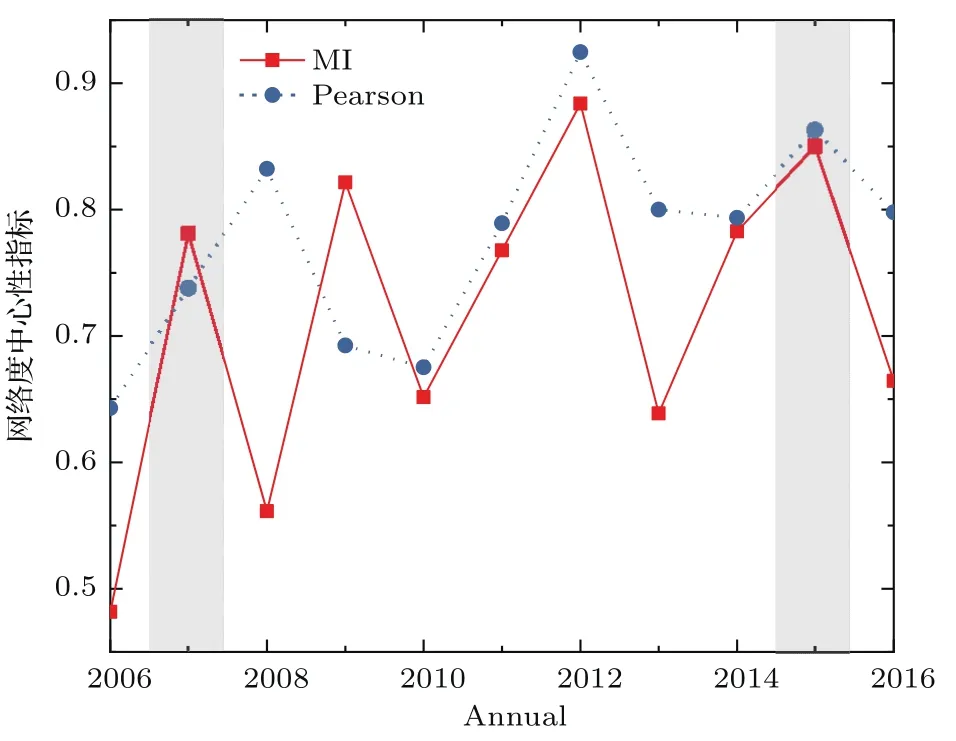
图7 TN网络的网络度中心性指标Fig.7.Network degree centralization of TN.

图8 TN网络的Jaccard指标Fig.8.Jaccard index of TN.

5 结 论

复杂网络被广泛地应用于金融领域,能够反映金融市场整体的拓扑结构、动态运行规律以及金融主体之间的相互依赖关系.本文使用文本互信息方法来度量地区金融指数节点的相关性,分别构建了MST与TN网络,并将其与Pearson相关系数的网络从节点相关度、网络拓扑指标数值大小、度分布的幂律检验以及动态网络特征等方面进行了对比,数值结果表明文本互信息方法在多数指标上优于Pearson方法.1)在金融网络中引入基于文本互信息的相关性度量方法,计算时不需要将样本人为离散化成几个不同的状态,也不需要假设样本服从Dirichlet分布;2)在阈值网络中提出使用分位数来确定阈值的方法,考虑到两种方法对比的实际需要,本文将数据6等分并取第4个区间的中点为阈值;3)将中国沪深两地证券市场按地区(不含港澳台)划分,并从复杂网络的角度对证券市场的空间性质进行研究,从中得出一些关于地区指数的结论;4)从地区金融网络的拓扑分析中可以看出,中国地区金融网络服从幂律分布;该网络具有动态的稳定性;一些经济欠发达地区处于网络中心位置,在分析中国沪深证券市场时不应该被忽略.

在计算动态指标时使用了静态阈值,由于金融市场存在波动率长程关联,下一步将考察动态阈值对指标的影响[48].此外,导致经济欠发达地区在地区复杂网络中重要的原因是什么,是因为这些地区股票家数过少,还是市场本身还有没被发掘的现象?这也是值得进一步讨论的工作.将本文提出的方法推广到其他金融领域如外汇市场,在引入量化系统后应用于实际投资以及金融危机的预测等也是值得研究的方向.