基于正交设计的大坝深层抗滑稳定敏感性分析
2018-10-29顾中明马春辉郭志辉
王 雯,顾中明,杨 杰,李 婷,马春辉,郭志辉
(1.西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西西安710048;2.河北工程大学水利水电学院,河北邯郸056038)
重力坝具有对地形、地质条件适应能力强、安全可靠等优点[1],在国内外水利工程中应用广泛。重力坝设计中,常遇见坝基内存在不利软弱结构面等情况,使重力坝的稳定难以保证,核算大坝的深层抗滑稳定便成为设计过程中的重要任务[2]。因此,进行重力坝深层抗滑稳定影响因素敏感性分析[3],确定对安全系数影响程度最高的因素,具有一定的工程实际应用背景[4]。
关于重力坝深层抗滑稳定影响因素的敏感性研究前人做了大量工作,Yuan[5]结合模型试验研究了不同软弱结构面下抗剪断参数对抗滑稳定安全系数的敏感性;李美蓉等[6]进行了断层混凝土置换深度对大坝抗滑稳定安全系数的敏感性分析;曹其光等[7]分析了分界面角度、抗力角、抗力体角度的变化对安全系数的影响;张博[8]研究了坝体重量、拉预应力锚索对安全系数的影响趋势。以上研究主要采用传统的敏感性分析方法,即以安全系数作为评判指标,计算中固定其它参数取值而改变某一参数取值,分析安全系数随这一变动参数的变化规律,提出其敏感性大小。这种方法未考虑到各参数变化过程中的相互影响,因此与实际情况存在差异[9]。
针对传统的深层抗滑稳定敏感性研究都是基于单因素变化的特点,本文基于正交试验法,以抗滑稳定安全系数作为试验评价指标,研究在多因素作用下重力坝抗滑稳定,分析各因素对大坝深层抗滑稳定影响的敏感程度和显著程度,为重力坝设计中深层抗滑稳定计算提供一定参考。
1 重力坝深层抗滑稳定分析
重力坝坝基软弱结构面多形成双滑动面。本文以双滑动面为计算模型,双滑动面示意图如图1所示。
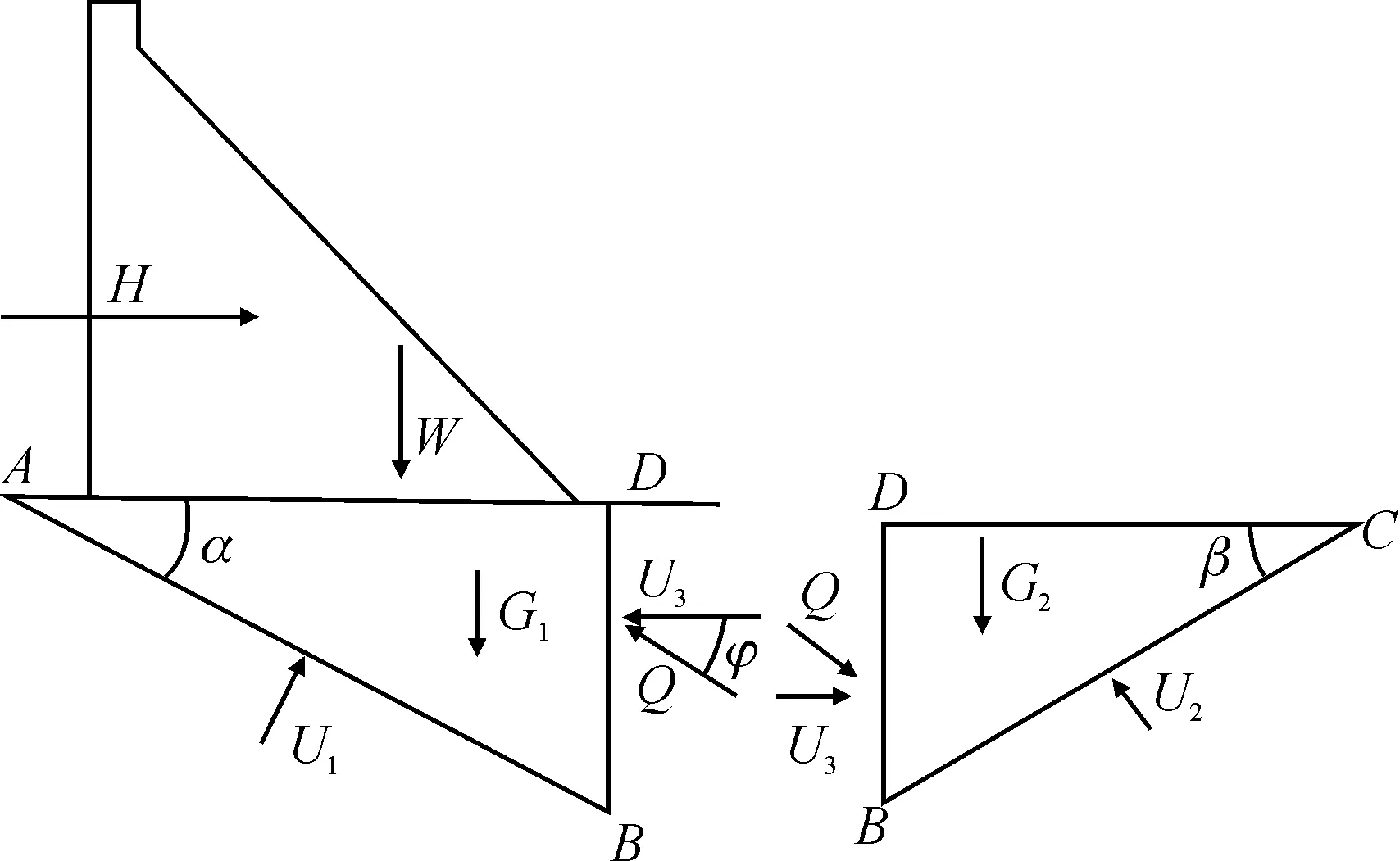
图1 双滑动面示意图Fig.1 Calculating diagram of three sliding planes
根据图1失稳模型,重力坝沿AB滑裂面形成滑动时,可将其上全部受力投影至AB面上。根据莫尔-库伦准则,AB面上抗剪断安全系数为:
(1)

将抗力体BCD所受的全部作用力投影至滑动面BC上,则沿滑动面BC的抗剪断安全系数表达式为:
(2)

通过刚体极限平衡法中等安全系数法,对重力坝深层抗滑稳定进行分析,令滑动体和抗力体同时处于极限平衡状态,即K1=K2,求得安全系数,并将其作为大坝稳定的评价指标。
2 正交试验设计方法
2.1 正交试验设计
试验方案选取各参数具有代表性的组合,根据“正交表”设计试验[9],通过这一过程可减少具体的试验组次。试验中将对考察指标G2具有影响的参数称为因素,针对因素进行比较的试验条件称为水平。正交表Ln(mk)中:L为正交表;n为试验次数;m为因素的水平数;k为因素个数。
2.2 正交试验结果分析
正交试验结果的数值分析主要有极差分析和方差分析两种方法:极差分析通过考察各影响因素的极差,由极差差异评价各因素影响的敏感性;方差分析主要对各影响因素的变异对总变异的贡献率进行分析,通过F检验来评价各因素对安全系数影响的显著性。
2.2.1 极差分析
假设j=A,B,…代表对考察指标有影响的各个因素;i=1,2,…,r为各因素的水平数;Ai表示因素A的第i水平;Xij表示影响因素j的第i水平值。在Xij下进行试验,得到正态分布的随机变量Yij;在Xij下进行n次试验得到n个试验结果Yijk(k=1,2,…,n),统计参数Kij为[10]:
(3)

极差分析法,即通过求出各因素在不同水平下指标值的最大值和最小值之间的差值(极差)来评价各个因素影响程度的大小,极差越大,表明该因素水平变化对考察指标影响越大,为主要因素;反之,则为次要或者不重要因素。其计算公式为:
Rj=max{K1j,K2j,…}-min{K1j,K2j,…}
(4)
式中,Rj为第j列因素的极差。
2.2.2 方差分析
1) 方差计算过程
各因素的偏差平方和与随机误差平方和构成试验结果的总偏差平方和。对各因素的偏差平方和与随机误差平方和进行对比,作F检验,判断因素影响是否显著。其计算过程为:
①计算总偏差平方和QT:
(5)
②计算各因素偏差平方和Qij:
(6)
③计算各因素均方差Mj:
Mj=Qij/(r-1)
(7)
④计算误差均方差MT:
(8)
⑤计算各因素对应Fj值:
Fj=Mj/MT
(9)
式中,s为因素的个数,即试验总次数n与因素水平数r的比值;自由度h为因素的水平数减1,即h=r-1。
2) 显著性检验
对于给定的显著性水平α(一般取α=0.025或α=0.01),先从F分布表中查出临界值Fα(F0.025、F0.01),将计算得出的Fj和与Fα进行对比: 若Fj>F0.01, 则称因素j对试验结果敏感性高,影响效果高度显著; 若F0.025 某重力坝工程的地勘结果表明,非溢流坝段24#位于断层结构处,其走向NE30~40°,倾向NW58~65°,构成主要为破碎正长斑岩,区域地质平面图如图2所示。 由于坝址区断层的存在,可能引起重力坝坝基失稳,因此核算坝基深层抗滑稳定是本工程的重要任务。具体坝基力学参数如表1所示。 表2 各水平因素值Tab.2 Value and level of each factor 根据正交设计并考虑误差项,制定L25(56)正交表。采用刚体极限平衡法,分别计算各工况下大坝抗滑稳定安全系数,研究在多因素共同作用下大坝的稳定性。K为双斜面失稳模式下安全系数,试验结果如表3所示。 表3 试验方案及安全系数结果Tab.3 Experimental scheme and safety factor results 目前,关于大坝深层抗滑稳定影响因素的敏感性研究主要集中于单因素分析,单因素分析法能直观反映出单个因素对指标的影响趋势,但无法明确表明某个因素变化对抗滑稳定安全系数影响的大小,存在一定的局限性。鉴于此,本文基于正交试验法,对重力坝深层抗滑稳定具有影响的因素进行敏感性分析及显著性检验。 3.3.1 极差分析 依据表3的试验结果,采用刚体极限平衡法下安全系数作为评价指标,对各影响因素进行极差分析,分析结果如表4所示。 表4 极差分析表Tab.4 Table of the range analysis 3.3.2 方差分析 极差分析具有简单直观、计算量小等优点,但是无法估计试验误差大小,无法精确地评价各因素对指标的影响程度,为提高评价准确性,进一步采用方差分析来对因素敏感性进行分析。 当显著性水平α为0.01、0.025时,有F0.025(4,4)=9.6、F0.01(4,4)=16.0。当Fj 实际工程中,针对存在软弱夹层的地质条件,可采取混凝土回填、固结灌浆、混凝土塞、预应力锚索等措施对可能存在的滑裂面和软弱夹层进行处理。浅层处理可直接挖除后进行混凝土回填,深层滑裂面则通常采用混凝土塞的方式或设置混凝土深齿墙[11],通过增大抗剪断能力或改变滑裂面形式来提高滑动体的抗剪断系数。 表5 方差分析表Tab.5 Table of the variance analysis 3) 浅层处理可直接挖除后进行混凝土回填,深层滑裂面可采用混凝土塞的方式或设置混凝土深齿墙,通过增大地基抗剪断能力或改变滑裂面形式来提高滑动体的抗剪断系数。3 工程实例分析
3.1 工程概况
3.2 正交试验设计

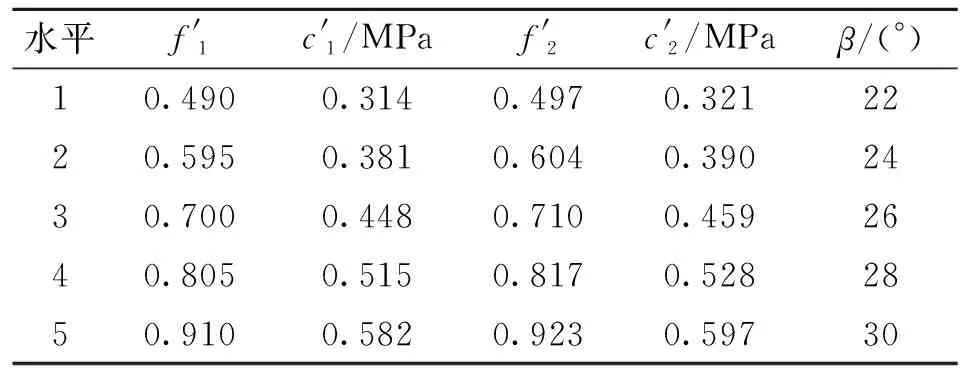

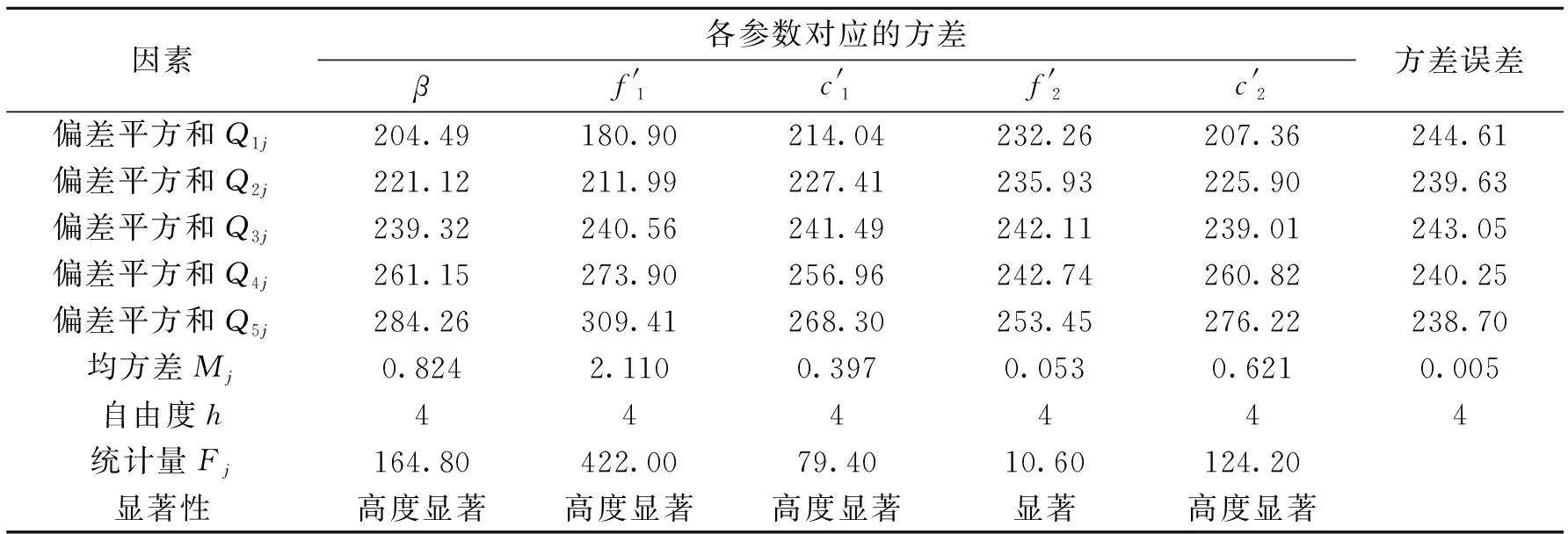
3.3 敏感性分析

4 结 论

