水平小圆管内超临界二氧化碳对流传热特性的试验研究

2018-10-29王军辉郭鹏程颜建国朱凤岭罗兴锜

西安理工大学学报 2018年3期

王军辉,郭鹏程,颜建国,朱凤岭,罗兴锜

(西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西西安710048)

超临界流体流动换热是能源转换与利用领域中的研究热点之一。二氧化碳因其临界参数较低,且储量丰富、安全经济等诸多优势,在很多新技术领域得到了广泛的应用,如超临界CO2布雷顿循环、微小型高效换热器、新型热泵、制冷等领域[1]。在这些应用中,都涉及到超临界CO2在小通道内的流动与传热特性[2]。

由于众多新技术的需求,从20世纪60年代开始,人们对超临界流体的传热特性进行了广泛的研究。在超临界状态下,没有气液两相的区别,而且在临界点附近,流体物性变化十分剧烈,这也导致传热规律与单相及两相流体存在明显差异。在超临界大比热区以外,流体传热规律可以按照单相流体来处理,但在大比热区内,传热规律十分复杂,目前仍未有满意的答案[3]。

石润富等[4]对水平管内二氧化碳的换热特性进行了不同工况下的试验研究,发现增大质量流速,降低压力等因素对水平管中超临界二氧化碳的传热特性有较大提高。Liao[5]通过试验研究发现,当超临界二氧化碳在水平管内冷却换热时,试验数据与大管径传热关联式有较大出入,而且加热工况和冷却工况的传热数据也不一致。相梦如等[6]对超临界压力CO2在水平管内于冷却条件下的对流换热进行了数值研究,结果表明,浮升力使流体出现温度场不对称现象和二次流,下壁面的对流换热系数比上壁面先达到峰值。Jiang[7]就超临界二氧化碳在竖直圆管中的对流传热进行了试验和数值模拟,结果显示,流动方向、流速等因素对传热影响较小,没有出现传热恶化的现象。张宇等[8]对低雷诺数下竖直圆管中超临界二氧化碳的对流换热进行了试验研究,结果显示,在热流密度较高时,浮升力作用明显,流体的换热能力增强。杨传勇等[9]对超临界二氧化碳对流换热进行了数值模拟,研究发现,二次流和范宁摩擦系数在管道进口段的变化最剧烈。刘生晖等[10]对管内对流传热的浮升力进行了数值模拟,研究发现,水平管内在高热流密度和低质量流速的工况下,浮升力对流体的换热能力影响很明显。Xu等[11]对螺旋管内二氧化碳换热特性进行了试验研究,发现由于在螺旋管内流动时增加了流体的湍流程度,同时浮升力以及重力因素对流体换热因素的影响加剧,使得螺旋管内流体的传热效率高于直管。

虽然文献中已经有较多针对超临界CO2传热的研究,但针对小通道内的传热研究仍不够完善,由于超临界流体复杂的热物理特性,仍需开展相关试验研究。

本文研究超临界CO2在水平小圆管内(内径2 mm)的对流传热特性,采用交流电直接加热金属管道产生均匀热流,获取了超临界CO2的传热系数,并分析其影响因素。

1 试验介绍

1.1 试验系统

图1为超临界CO2对流传热试验回路的示意图。整个试验回路为闭式循环回路。主要设备包括高压恒流泵、质量流量计、工业水冷机、水冷换热器、背压阀、高压二氧化碳储液罐等。试验中二氧化碳在被通入回路之前,整个回路被抽真空以排除其他气体杂质。二氧化碳经冷却后,以液态形式储存在高压储液罐中。储液罐中的CO2由高压恒流泵提供动力,进入试验段加热,试验之后的CO2被冷却后再次进入储液罐,从而形成闭式循环回路。

采用低电压、大电流的交流电通过试验管道,依靠金属管道本身的电阻产生焦耳热,从而对管道中的流体进行加热。

图1 试验系统示意图Fig.1 Schematic diagram of experimental loop

1.2 试验段

试验段为水平放置的不锈钢圆管,规格为φ3×0.5 mm,有效加热长度为450 mm,如图2所示。试验段外壁的上下面布置K型热电偶丝(共5个截面,10个测温点)。试验段外表面缠有适当厚度的保温棉,一方面减小散热损失,另一方面可以保证外壁温测量稳定。

进口及出口的流体温度由φ1.5 mm的T型铠装热电偶测量。采用Rosemount 3051压力变送器和差压变送器分别测量系统压力及试验段压差。采用西门子质量流量计测量试验段质量流量。所有的原始数据由IMP3595分布式数据采集系统进行采集。

图2 试验段示意图Fig.2 Schematic diagram of test tube

1.3 试验工况

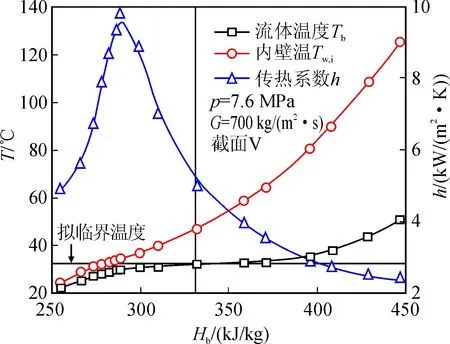
本试验参数范围:系统压力p取7.6、8.2、8.9 MPa,质量流速G取700、1 100、1 400 kg/(m2·s),热流密度q取0～360 kW/m2,流体温度Tb取17～81 ℃,雷诺数范围为1.8×104

表1 工况表Tab.1 Test conditions

1.4 数据处理方法

在正式试验前,需要进行热平衡试验以确定系统的热效率η,计算公式为:

(1)

式中,m为质量流量(kg/s);Hb,i和Hb,o为进出口流体的焓值(kJ/kg),由REFPROP物性程序获得;U为加热电压(V);I为加热电流(A)。本试验的平均热效率为96.52%。

试验段内壁热流密度计算公式为:

(2)

式中,di为加热管内径(m);L为有效加热长度(m)。

当地流体焓值分布按线性分布处理,z处横截面上平均流体焓值Hb为:

(3)

式中,z为从试验段加热起始点计算的长度(m)。局部流体温度Tb,loc根据局部焓值及压力,由REFPROP物性程序查取。

根据含内热源的一维稳态导热方程,可由金属管的外壁温Tw,o推算其内壁温Tw,i,计算公式为:

(4)

式中,di和do分别为试验段的内径和外径(m);λw为试验段金属管导热系数(W/(m·K))。

本试验中, 导热系数变化幅度不大, 可取为常数17 W/(m·K)。

对流传热系数为:

(5)

式中,h为传热系数(kW/(m2·K));Tb为流体温度(℃)。

1.5 误差分析

对于一个间接测量值Y,假设由若干个直接测量值Xi合成,则相对不确定度为:

(6)

式中,N为直接测量值的个数。

根据上述误差传递公式,求出本试验中主要参数的不确定度,结果如表2所示。

表2 参数的不确定度Tab.2 Uncertainties of the experimental parameters

2 试验分析

2.1 试验台校验

为了保证试验精度,在进行超临界CO2传热试验之前,首先采用去离子水对试验台进行传热验证性校验。校验试验所用工质是用离子交换法制成的去离子水,硬度为0,电导率小于50 μS/m,可以保证受热管壁面不结垢、不腐蚀,从而保证流动和传热过程的可靠性。

对于管道内旺盛紊流的流体与壁面间的单相对流传热,目前普遍采用的是Dittus-Boelter公式:

Nu=0.023Re0.8Pr0.4

(7)

图3表示了单相去离子水传热的标定结果。

图3 去离子水传热标定Fig.3 Validation of the experimental system using deionized water

如图所示,Nu数试验值与经典公式的预测值吻合良好,试验值与预测值的误差在±10%范围内。标定结果表明,本试验回路的精度满足需求,相关测量仪器及数据处理方法也都可靠。

2.2 超临界CO2的热物性

超临界流体是没有气体和液体差异的均匀相。超临界流体既有类似液体的密度,又有类似气体的传输特性,低黏度与高扩散系数有利于传质过程。与单相及两相流体相比,超临界流体热物性具有明显的特殊性。

CO2的临界压力和临界温度分别为7.38 MPa及30.9 ℃。在超临界压力下,另外一个重要参数是拟临界温度,它是指在某一给定压力下,流体比热容峰值所对应的温度。在拟临界温度附近,超临界CO2的物性变化异常剧烈。

图4表示了7.6 MPa时,CO2的物性随温度的变化情况。该压力对应的拟临界温度为32.3 ℃,此时比热存在显著的峰值。在拟临界温度附近,随温度的增加,密度和粘度出现了骤降;导热系数在拟临界温度之前出现了窄范围的局部增加。尽管超临界流体不存在气液两相的转变,但剧烈的物性变化会造成特殊的传热现象,超临界流体的传热规律尚未被清晰地揭示。

图4 p=7.6 MPa时超临界CO2热物性Fig.4 Thermo-physical properties of supercritical CO2at p=7.6 MPa

2.3 壁温分布特性

图5表示了在工况p=7.6 MPa,G=700 kg/(m2·s),不同热流密度下,试验段轴向壁温的分布情况。在较低热流下(如q=102.38 kW/m2),管内传热近似于单相传热,壁温沿流动方向缓慢增加。随着热流增大(如q=191.55 kW/m2),轴向壁温分布呈现出先降低后升高的趋势。

该现象的主要原因在于,沿着流动方向,管内工质温度逐渐增加,当温度接近拟临界点时,比热显著增加,传热强化,换热温差减小,壁温降低。当温度进一步增加时,流体逐渐远离拟临界区,且密度和导热系数都较低,状态类似于气体,由此传热弱化,换热温差增加,壁温显著升高。

图5 轴向壁温分布Fig.5 Distributions of axial wall temperature

2.4 传热系数

图6表示了在p=7.6 MPa,G=700 kg/(m2·s)工况下,最后一个横截面处(截面V)的流体温度、内壁温及传热系数的变化曲线。试验段进口保持恒定温度(约17.5 ℃),逐步提高热流密度(如q取0～191.55 kW/m2)。

在p=7.6 MPa时,二氧化碳的拟临界温度为32.3 ℃。当内壁温和流体温度都低于拟临界温度时,管内CO2类似于液态,随着热流增加,内壁温和流体温度都缓慢增加,传热系数小幅增加。当内壁温大于拟临界温度,而管道流体温度仍小于拟临界温度时,传热系数存在明显的峰值。这是因为,近壁区的CO2率先进入超临界状态,近壁区流体的吸热能力显著增加,且近壁区流体的粘性较小,Re数较大,边界层厚度减薄,有利于传热过程。另外,近壁区流体的密度较小,主流体的密度较大,密度差引发的浮升力将进一步促进近壁面和主流体之间的热质交换过程。

图6 传热特性曲线Fig.6 Heat transfer curve at Section V

在本文研究的工况中,在特定截面处,流体温度达到拟临界温度之前,传热系数存在一个明显的峰值。本文发现,采用液膜温度可以预测传热峰值。液膜温度Tfilm的定义为:

(8)

即液膜温度为当地流体温度与内壁温的平均值。

图7 传热系数与膜温的关系Fig.7 Relationships between heat transfer coefficient and film temperature

结果表明,当液膜温度达到拟临界温度时,传热明显强化,传热系数出现峰值。图7是一个典型的工况,p=7.6 MPa,G=700 kg/(m2·s),截面V处,当液膜温度为32.3 ℃(拟临界值)时,传热系数处于峰值区。

2.5 热工参数的影响

图8表示了质量流速对超临界CO2传热的影响。选取p=7.6 MPa,G取700、1 100、1 400 kg/(m2·s),截面V处的数据。如图所示,随着质量流速的增加,传热系数在所有区域都有所增加。

图8 质量流速对传热系数的影响Fig.8 Effect of mass flux on heat transfer coefficient

图9表示了系统压力对超临界CO2传热的影响。选取G=1 100 kg/(m2·s),p取7.6、8.2、8.9 MPa,截面V处的数据。如图所示,p=7.6 MPa时,拟临界温度区内的传热明显强化,传热系数峰值明显,随着压力升高,传热强化的效果减弱。这是因为越靠近临界压力,拟临界区物性的变化越剧烈,如比热峰值更显著等,这些因素使得传热过程得到强化。