轻钢住宅结构整体抗震性能的影响研究

2018-10-29潘秀珍赵登云田建勃

西安理工大学学报 2018年3期

潘秀珍,赵登云,刘辉,张鹏,田建勃

(1.西安理工大学土木建筑工程学院,陕西西安710048;2.中交第一公路勘察设计研究院有限公司,陕西西安710075;3.陕西省建筑科学研究院工程抗震研究所,陕西西安710082)

轻钢住宅结构体系是以轻型钢构件,包括冷弯薄壁型钢、热轧或焊接型钢、焊接或无缝钢管及其组合构件作为主要承重骨架,并采用轻质围护材料的低、多层钢结构[1-2]。结构体系通常有纯框架结构体系、冷弯薄壁型钢结构体系、交错桁架体系、框架-支撑体系等,轻钢住宅结构组成见图1。该体系具有质量轻、空间布置灵活、可标准化生产、建设周期短、抗震性能好、节能环保等优点,在我国具有很好的应用前景[3-4]。

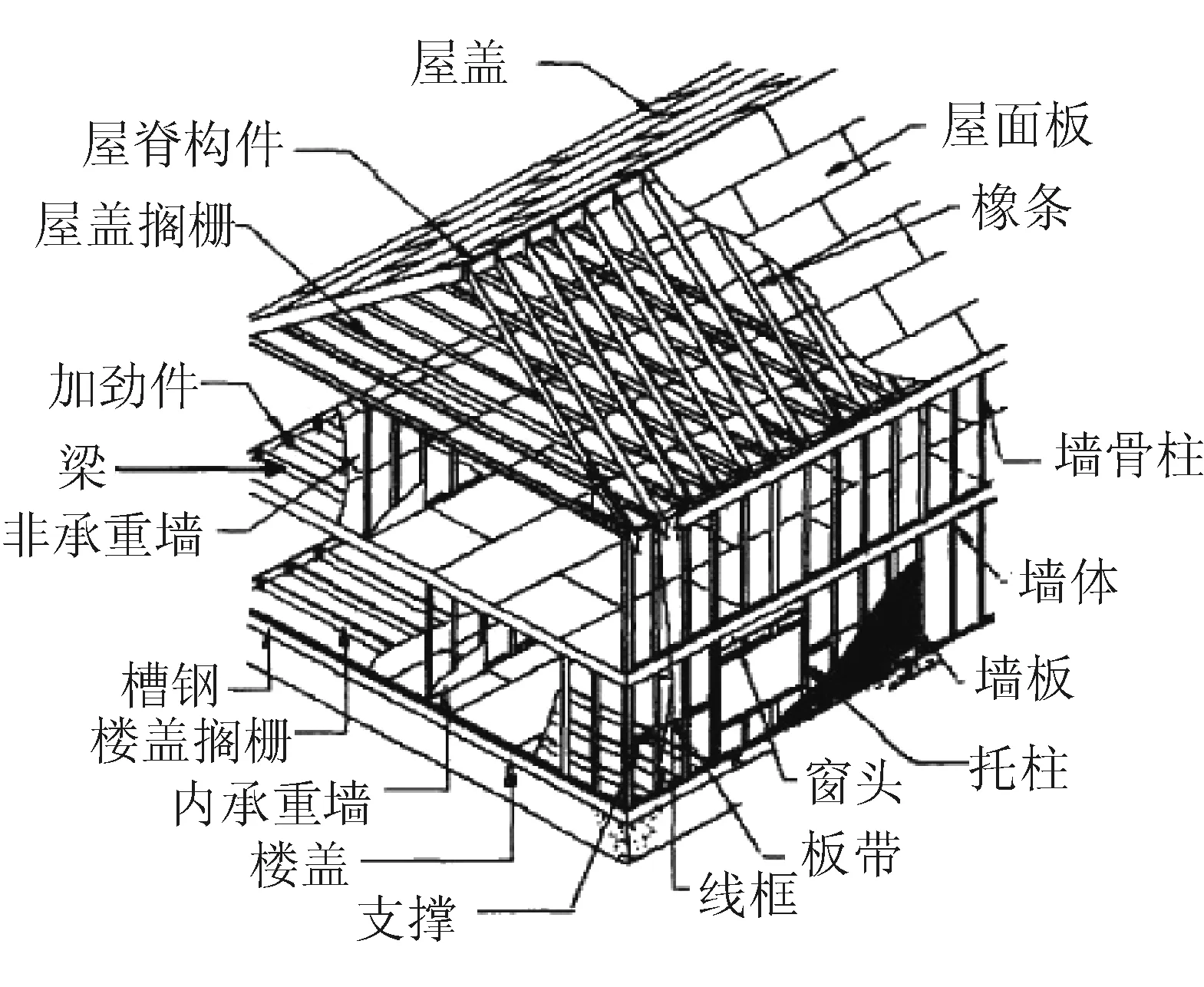
图1 轻钢住宅结构示意图Fig.1 Diagram of light steel structural resident

目前该种体系大多建成两层或者局部三层,随着土地紧张、居住者对居住面积需求增加,将该体系逐渐用于多层,保证其整体抗震性能是一个急需研究的问题[5-6]。

目前国内外对轻钢住宅结构的研究主要集中在单片轻钢复合墙体、单根梁柱或者构件连接方面。在轻钢复合墙体方面,墙体覆面板对于墙体的抗侧承载力及抗侧刚度提升较大,能够显著提升墙体的抗侧移能力[7-9]。其次,墙体蒙皮的作用也非常明显,其对墙体的竖向承载力、稳定性、刚度都有着几乎成倍的提升[10-13]。作为主要受力构件的桁架梁,在不同的结构形式中对结构整体抗震性能都有着较大的影响[14]。通过改善轻钢龙骨墙体与钢框架的连接形式可以使结构拥有更好的延性性能,达到“强连接弱构件”的设计理念[15-17]。另外自攻螺丝对于构件之间的传力也起着非常关键的作用,国内外的研究主要集中在自攻螺丝的抗剪抗拉方面,而对于疲劳问题的研究较为缺乏[18]。目前对影响轻钢住宅结构整体抗震性能的因素,如结构体系的高度、开间及进深,楼板刚度等方面的研究较少。本文针对以上研究的不足,着重分析结构体系的高宽比、开间数等对结构整体抗震性能的影响,并提出相关设计建议,以促进轻钢住宅结构在我国抗震设防区的推广与应用。

1 模型设计

轻钢住宅结构竖向受力构件的几何平面尺寸见图2(a),其中方钢管柱的截面尺寸为40 mm×40 mm×1.5 mm;其与V形连接件的位置关系见图2(b),在方钢管柱的底部和顶部各布置一根截面规格为240 mm×40 mm×1.5 mm的槽钢;沿方钢管柱高度方向布置两道横撑,规格与方钢管柱相同;V型连接件所用型号为中型,高190 mm,厚1.5 mm;斜拉钢带宽100 mm,厚1.5 mm。这些基本构件通过自攻螺钉连接形成桁架梁、桁片柱、四方柱和墙体,自攻螺钉均为WL型,直径为8 mm。

由于轻钢龙骨可以形成大开间、大进深,该结构体系用于住宅结构时,小开间、小进深的厨房、卫生间等功能用房通常采用轻质隔墙进行分隔,否则会造成房屋造价成本提高,不经济。考虑到实际工程中内部轻质隔墙一般为脆性材料,对结构整体抗震性能影响不大,仅起到功能分区的作用,因此在有限元建模时,仅对结构体系中的轻钢龙骨墙体进行建模,忽略内部隔墙的作用。以四开间的轻钢住宅为代表,主体结构平面布置见图3。所有模型的层高均为3 m,开间尺寸为3 m,内外墙的厚度均为240 mm,桁架梁柱间距为600 mm,角柱及门窗洞口处柱子均采用由桁片柱组成的四方柱。外墙采用竹胶板材料,厚度为8 mm;屋面板及楼板采用强度等级为C30的混凝土,厚度均为50 mm。

图2 单片轻钢龙骨构件尺寸Fig.2 Specimen size diagram

图3 结构平面布置图Fig.3 Layout of the structure

2 有限元模型的建立

2.1 轻钢龙骨的有限元分析验证

为了保证有限元分析结果的准确性,首先对图2中的轻钢龙骨墙体[19]进行了理论计算并与试验结果比较。模型的几何尺寸、材料性能、边界条件、加载方式完全与文献[19]中的试验相同。Q235钢材的弹性模量、本构关系均取自文献[19]板材拉伸试验数据,见表1,泊松比μ=0.3。

采用有限薄膜应变、线性、四边形壳单元S4R建模,采用Von Mises屈服准则及双线性随动强化准则,利用ABAQUS建立框架的有限元模型,其网格划分见图4。当墙体中受拉钢带Mises等效应力超过材料中的屈服强度,认为墙体失去抗侧移承载力,也即墙体发生破坏。

图4 墙体网格划分图Fig.4 Mesh figure of wall

试件在水平单向荷载作用下的Mises应力云图见图5。

图5 Mises应力云图Fig.5 Mises stress nephogram

在加载初期,墙体发生均匀侧向变形,受拉钢带的应力逐渐增大,且在与桁架柱连接处产生很大的应力;当位移荷载达到13.2 mm时,受拉钢带的Von Mises应力达到屈服强度;继续加载,墙体侧向变形速度开始加快,墙体上下部槽钢发生局部屈曲,受压钢带发生弯曲变形,最终整个墙体失去承载力。文献[19]中墙体试件的破坏以剪切形变形为主,见图6。水平抗力几乎完全由钢带承担,螺钉没有被剪坏,极限破坏以钢带屈服告终。有限元模拟的破坏形态与试验现象基本一致。

图6 试验破坏图Fig.6 Wall damage figure

有限元墙体模型和试验墙体的荷载位移曲线对比见图7,由表2列出的有限元模拟与试验结果对比可以看出:有限元计算得到的屈服荷载比试验结果低4%,相应的屈服位移则比试验结果低25%。产生这种偏差首先是因为试验中各构件间均由自攻螺钉连接,而有限元建模没有考虑螺钉连接的具体情况,对其进行了简化;其次轻钢构件在试验加工过程中必会存在一定的初始缺陷、尺寸偏差等,而有限元建模并未考虑这些因素;最后由文献[19]描述的试验过程可知,在施加水平拉力时,由于千斤顶滚轴动作不灵,产生很大偏斜,即试验加载装置问题也导致有限元模拟与试验结果出现偏差。综上分析可知,有限元分析与试验结果相比具有一定的精度,可以为后续建模分析提供一定的理论基础。

图7 荷载位移曲线Fig.7 The load displacement curve

屈服荷载/kN屈服水平位移/mm试验22.517.5有限元模拟21.613.2有限元值/试验0.960.75

2.2 整体模型的建立

2.2.1 基本假定

建立有限元模型时,既要保证模拟的精度,又要减小计算工作量,特做如下基本假定。

1)考虑墙体的蒙皮效应,竹胶板和桁架柱粘结在一起,不考虑两者之间的滑移作用,也即忽略自攻螺钉的作用。

2)考虑到轻钢住宅结构中楼板厚度较小,通常在50～80 mm之间,本文将混凝土楼板假定为弹性楼板,考虑其与桁架梁的组合作用效果。

3)忽略门窗洞口上下部分墙体以及墙体结构中桁片柱之间横撑的影响,看作是结构的安全储备。

2.2.2 材料性能

由于结构体系包含钢、竹胶板、混凝土三种材料,因此需要考虑材料非线性。钢材简化为各向同性材料,材料特性见表1。混凝土简化为各向同性弹性材料,弹性模量E=2.09×104N/mm2,泊松比μ=0.2;竹胶板简化为正交各向异性弹性材料,材料类型定义为Lamina,共有E1、E2、u1、u2、G12、G13、G23七个参数,不考虑层间剪切特性,可将G13与G23设为接近于零,其他五个参数为:E1=6 123 MPa,E2=6 123 MPa,u1=0.127,u2=0.127,G12=550 MPa。

2.2.3 单元类型及网格划分

桁架梁、桁架柱、竹胶板、屋面板及楼板均采用三维壳单元S4R模拟。网格划分时根据结构的受力特点,不同部位划分的大小不同,方钢管、V型连接件及槽钢的网格尺寸为0.04 m,竹胶板网格尺寸为0.3 m,屋面板及楼板的网格尺寸为0.24 m。整体模型的网格划分见图8。

2.2.4 边界条件及构件相互作用设置

约束结构底层柱脚三个方向的平动与转动,以达到与基础刚接的效果。实际工程中,桁片柱的顶端仅用少量自攻螺钉连接在槽钢上,因此在有限元建模时桁片柱与顶梁和楼板的连接设置为铰接。整体结构中桁架梁与屋面板及楼板之间的连接、竹胶板与桁架柱之间的连接、桁架柱与顶梁及楼板之间的连接均采用“tie”约束模拟,其中桁架柱定义连接区域时只取钢管外侧边缘,从而实现其与顶梁和楼板铰接。

图8 三层轻钢住宅有限元模型Fig.8 The finite element model of three web steel residential

3 轻钢住宅结构整体抗震性能的影响研究

保持横向宽度不变,改变层数实现高宽比的改变,共建立5个模型,同时为了避免楼板开洞位置对结构抗震性能的影响,保持楼梯间位置不变,进行高宽比对轻钢住宅结构整体抗震性能的影响研究。5个模型的具体参数情况见表3。

表3 模型参数Tab.3 Model parameters

3.1 结构的自振频率

对轻钢住宅模型M-11～M-15进行模态分析,用ABAQUS/Standard提供的Lanczos特征值方法,得到结构前十阶自振频率,在此仅列出前四阶自振频率,按照不同层数分组对比,结果列于表4中。

由表4所列出的频率与周期可知,当轻钢结构的层数(高宽比)增加时,频率逐渐减小,周期相应逐渐增大。相较于二层结构,三、四、五、六层结构的第一阶自振周期分别增大了47%、98%、162%、218%,层数每增加一层的平均增幅为54%,自振周期的增长与层数的变化基本呈线性关系。随着层数的增加,结构第一阶自振周期增大的幅度要明显大于其它振型。结构各阶自振频率降低的幅度不同,但随层数的增加逐渐趋于平缓。

表4 不同层数结构的自振频率及周期Tab.4 Vibration frequency and period of different aspect ratio structures

3.2 结构的振型云图

振型云图既能反映结构的相对位移,又能反映结构的基本振型。对轻钢结构M-11～M-15进行模态分析,得到了前四阶振型图,限于篇幅本文只列出了五榀模型第一阶沿Y向的振动,见图9。可以看出:五榀模型的前四阶振型相似,增加结构的层数并未改变结构的大致振型,结构的第一阶振型均为Y方向的倒三角形整体侧向振动,第二阶振型为X方向倒三角形整体侧向振动,第三阶振型为整体扭转振动,第四阶振型为Y方向单波形整体侧向振动,最大侧向变形位置随着层数的增加有逐渐上升的趋势。

图9 M-11～M-15第一阶振型Fig.9 The first vibration mode of M-11～M-15

3.3 结构顶点位移时程反应曲线

对M-11～M-15输入EL-Centro波和Taft波,分别计算结构在7度、8度多遇和罕遇地震作用下的反应,通过结果数据整理,得到模型的顶层时程反应曲线，因篇幅有限在此仅列出EL-Centro波作用下的时程反应曲线，具体见图10。

图10 M-11～M-15的顶层位移时程反应曲线Fig.10 Displacement time history curves of top floor of M-11～M-15

可以看出：对于同一个模型，随着地震波加速度峰值的增大，结构顶层位移相应地呈线性增大,且各阶段顶层位移反应时程曲线形状大体一致;对于不同的模型,随着高宽比的增加,时程曲线由密变疏,表示结构的周期在逐渐变大,这与模态分析所得结果一致。

提取顶点的最大位移,得到不同地震烈度对应的结构顶点位移绝对值最大值,进行统计分析后发现:在EL-Centro波作用下,随着高宽比的增加,结构的顶点位移逐渐增大。以8度罕遇为例,M-12、M-13、M-14、M-15相较于M-11,顶点绝对位移分别增大了92%、313%、465%、583%。在Taft波作用下,多遇地震时结构顶点位移随高宽比的增加而增加,罕遇地震时,M-12出现顶层位移异常增大的现象,这是M-12的固有特性与地震波在某时段较为接近,所以位移出现突变。以8度罕遇为例,M-12、M-13、M-14、M-15相较于M-11,顶点绝对位移分别增大了338%、161%、397%、557%。

同一模型在不同烈度地震波作用下位移绝对值最大值出现的时间基本一致。M-11～M-15在EL-Centro波作用下,最大值分别出现在2.14 s、4.34 s、1.76 s、1.84 s、2.32 s,在Taft波作用下则分别出现在2.02 s、2.55 s、4.7 s、3.02 s、3.18 s。最大位移出现的时间与地震波峰值出现的时间不一致,其中两种地震波峰值均出现在1.62 s,这说明结构的地震反应除受地震波峰值的影响外还与自身频率、持时的影响有关。

3.4 楼层相对位移分析

楼层相对位移能够反映结构的整体变形情况,通过数据整理,提取出每个楼层在同一时间的位移绝对值最大值,8度地震波作用下的结构楼层相对地面位移分别列于图11和图12中。其中:λ=1～3分别对应不同高宽比的模型M-11～M-15。可以看出,在各地震波作用下,各结构最大楼层位移由下而上均匀增长,没有发生局部突变,结构侧向刚度较为均匀。

图11 EL-Centro波作用下结构楼层相对地面位移Fig.11 Displacement of each story under the EL-Centro earthquake wave

图12 Taft波作用下结构楼层相对地面位移Fig.12 Displacement of each story under the Taft earthquake wave

EL-Centro波作用下,对于同一个模型,随着地震波加速度峰值增大,结构楼层位移相应增大;在相同地震工况下,结构楼层位移随着高宽比的增大相应增加。

Taft波作用下,多遇地震时,结构楼层位移随着高宽比的增大相应增加,罕遇地震时,M-12楼层位移异常增大,这是因为M-12的固有频率与地震波在某时段的频率较为接近的原因。

3.5 层间位移角分析

根据层间位移,计算出每一楼层在不同地震波作用下的层间位移角,8度地震波作用下各个楼层的层间位移角见图13～14,整体模型在不同地震波作用下的最大层间位移角见表5所示。

可以看出:对于同一模型,随着地震波的增大,层间位移角相应增大,每一楼层的层间位移角并不随着楼层高度的增加而增加,而是先增大后减小,在某一楼层的层间位移最大,也即出现薄弱层。从薄弱层向上和向下的楼层层间位移角逐渐减小,因此在结构设计中若能提高薄弱层的刚度,结构的整体抗震性能也会大大提高。

在EL-Centro波作用下,M-11～M-15的薄弱层分别出现在第一、二、二、四、四层,随着结构高宽比的增加有逐渐上升的趋势。根据《轻型钢结构技术规程》[20],轻钢龙骨体系结构在多遇地震作用下弹性层间位移角不宜大于1/300,在罕遇地震作用下弹塑性层间位移角不应大于1/100,由表5可知M-15在8度罕遇地震作用下薄弱层弹塑性层间位移角为1/91,不满足规范的要求,而其他模型结构在多遇、罕遇地震作用下均能满足规范要求。

图13 EL-Centro波作用下结构层间位移角Fig.13 Drift of each story under the EL-Centro earthquake wave

图14 Taft波作用下结构层间位移角Fig.14 Drift of each story under the Taft earthquake wave

在Taft波作用下,M-11～M-15的薄弱层分别出现在第一、二、二、四、四层,其中M-14在第四层也出现了层间位移角突然增大的现象,也为结构薄弱层,各结构在多遇、罕遇地震作用下均满足规范要求,但M-15在8度罕遇地震作用下为1/106,已经非常接近规范中轻钢龙骨体系结构弹塑性层间位移角限值1/100,地震作用下结构安全性低。

综合以上分析,建议在8度抗震设防区的轻钢结构高宽比不宜大于2.5。