一种自抗扰控制凹印套准系统研究

2018-10-29卫延斌张海燕梁志欣

西安理工大学学报 2018年3期

卫延斌,张海燕,梁志欣

(西安理工大学印刷包装与数字媒体学院,陕西西安710048)

凹版印刷因其印刷速度快、印刷幅面宽、墨层厚实、网点再现性好、层次丰富、颜色鲜艳、印版辊耐印率高、印品质量稳定和有一定防伪性等一系列优势,在图文出版领域,尤其在软包装印刷领域占据了绝对主导地位[1],已成为仅次于平版印刷的第二大印刷方式。近年来,随着“低碳经济”和“环保安全”意识的增强,绿色节能、高效环保已成为印刷设备的重要考虑因素,研发高速度、高精度、高成品率凹印设备已成为印刷装备制造业新的发展目标。自动控制方面,随着伺服系统与现场总线技术的快速发展,无轴传动技术在为凹印机机械结构带来巨大简化的同时,也对套准系统的控制提出了更高的要求,如何建立无轴传动模式下多色套准系统的准确模型,设计研究高性能套准控制系统已成为提高凹印机性能的关键问题[2]。

凹印机套准误差包括横向误差和纵向误差,其中,横向误差主要受辊间平行度影响,可通过调整各辊间平行度消除,对套印误差影响不大;纵向套准误差则主要取决于各版辊的速度、色组间的料带张力、料带特性等因素,同时还受制造和安装误差的影响,是套准系统控制的难点所在[2,3]。Yoshida等[4]对机械长轴传动和无轴传动下的纵向套准系统分别进行了建模,并设计了简单的增益前馈控制器,但模型建立过程中忽略的影响因素较多,导致模型不完善。Kang等[5]建立了套准系统的数学模型,设计了前馈PID控制器以抑制版辊速度波动产生的套准误差,但忽略了牵引段张力波动对套准误差的影响。Lee等[6]以引起套准误差的主要因素为核心设计了PID控制策略。李健等[7]对纵向套准模型做了推导,在所建立数学模型基础上设计了基于PID的前馈套准误差控制策略,仿真显示与传统PID控制相比能显著提高套准精度,但是缺乏实验验证。陈义君等[8]利用扩张状态观测器与前馈控制相结合,提出了一种多色套准系统解耦控制策略。刘善慧等[9]对凹版印刷套准系统用小偏差法线性化处理了其非线性耦合数学模型,并将前馈控制和自抗扰控制结合设计了多层套准系统的解耦控制器,但验证方面仅限于仿真,缺乏实验验证支持。

自抗扰控制(Active disturbance rejection control,ADRC)技术是一种结合经典调节理论和现代控制理论的非线性鲁棒控制技术,其精髓是系统内外干扰可通过扩张状态观测器主动估计,并在控制算法中实时进行补偿[10],这种特性非常适合干扰不确定的纵向套准。因此,本文以四色机组式无轴传动凹印机纵向套准系统为研究对象,推导建立了双色印刷套准模型,将双色模型扩展建立四色印刷套准模型,并针对模型设计了前馈ADRC套准控制器,仿真及实验结果均表明,该控制系统具有良好的抗干扰能力,实现了对凹印套准的高精度控制。

1 四色套准模型建立

1.1 双色套准模型建立

对凹版印刷相邻两机组印刷滚筒结构进行抽象简化,沿料带运动方向建立X轴坐标,将色组1所在位置作为坐标零点。图1为双色印刷色组模型示意图。

图1 双色印刷色组模型Fig.1 Two colors printing model

为了更好地建立模型,假定料带与滚筒间无滑动,且印刷过程中料带本身应变很小。假设在t<0时印刷机处于无扰动稳定状态,在t≥0后有扰动出现,色组1在t=t1时刻将色标1印至料带上,色组2在t=t2时刻将色标2印至料带,无干扰时色标1、2重合,有干扰时色标1、2不能重合,形成色组套准误差,则t2时刻套印误差e12(t2)为:

e12(t2)=X2(t2)-X1(t2)

(1)

式中,X1(t2)、X2(t2)为有干扰时t2时刻色标1、色标2的坐标值。

令ε01(t)为牵引段料带应变,ε12(t)为两色机组间料带应变,由质量守恒定律可得:

(2)

由于两色机组间料带应变ε12(t)变化很小,可近似认为dε12(t)/dt=0,带入式(2)可得:

(3)

对两色机组间料带长度有:

(4)

将式(4)带入式(3)可得:

V1(t)-V2(t)+ε12(t)·V1(t)-ε01(t)·V2(t)

(5)

式(5)中,考虑到ε01(t)为牵引段料带应变,量级很小,再乘以两色机组间的应变变化率则更小,故可略去不计,式(5)变为:

ε12(t)·V1(t)-ε01(t)·V2(t)

(6)

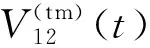
(7)

将式(7)带入式(3),可得:

(8)

(9)

设在印刷过程中料带任意位置受张力作用产生的应变为ε(x,t),则料带横截面积A(x,t)与应变的关系式为:

A(x,t)=[1+ε(x,t)]A01

(10)

式中,A01表示料带在牵引段未受到张力控制产生应变前的横截面积。

在时间t1到t2内,进入色组1滚筒的料带质量可表示为:

(11)

式中,ρ(t)为承印材料的料带密度;A12(t)为一、二色机组间料带横截面面积;x为料带运动方向变量;A01(t)为牵引段料带横截面积。

将式(10)带入式(11),两端积分并进一步简化可得t2时刻点色标点1坐标值为:

(12)

将式(12)和式(9)带入式(1),化简可得两色印刷单元在t2时刻套准误差为:

e12(t2)=

(13)

式中,T12表示t1时刻和t2时刻的时间差。考虑到料带未被拉伸时,即料带应变为0时,其套准误差应为:

(14)

(15)

对式(15)两端求导并略去小量可得:

(16)

一二色机组间实际套准误差E12(t)由安装在二色和三色滚筒之间的传感器测量,那么理论上应考虑二、三色之间的料带应变ε23(t),因此有:

(17)

联立式(6)、式(16)、式(17)可得双色套准模型:

(18)

1.2 四色套准模型建立

将双色套准误差模型扩展到四色印刷,四色印刷模型及套准误差检测如图2所示。

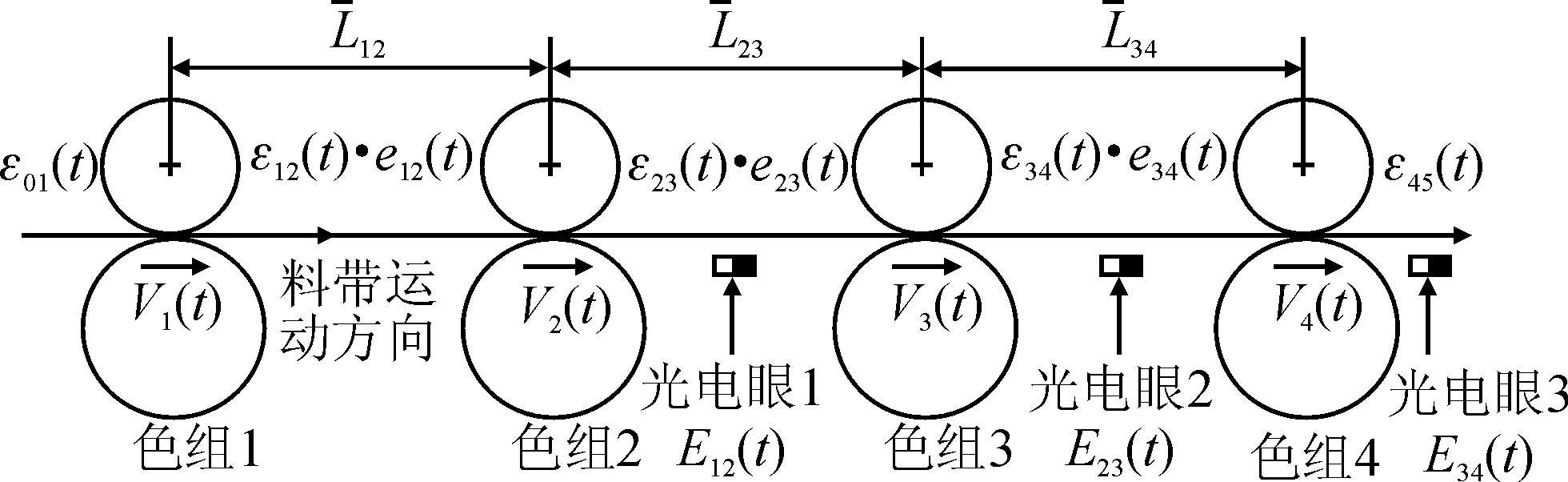
图2 四色印刷套准模型图Fig.2 Four colors printing register model

四色印刷套准模型可看作相邻两色套准系统串联,对双色模型进行扩展可得四色套准模型:

(19)

2 自抗扰四色套准控制系统设计

2.1 自抗扰控制器设计

自抗扰控制器由跟踪微分器(TD)、扩张状态观测器(ESO)、非线性误差反馈(NLSEF)三部分组合而成,是一种高品质的新型控制器。将微分跟踪器(TD)封装成一个子系统,封装好的微分跟踪器子系统包括一个输入v和一个输出v1;同样,扩张状态观测器(ESO)也封装成一个子系统,封装好的扩张状态观测器子系统包括两个输入y和u,两个输出z1和z2;非线性状态误差反馈(NLSEF)系统由一个函数组成,包括一个输入e和一个输出u0。

在Simulink模块上,基于自抗扰控制算法,建立微分跟踪器、扩张状态观测器和非线性状态误差反馈控制,将三者结合起来组成自抗扰控制器,如图3所示。

图3 自抗扰控制结构图Fig.3 Active disturbance rejection control structure

图3控制系统结构中,微分跟踪器(TD)的输出v1与扩张状态观测器(ESO)的输出z1做差后,作为非线性状态误差反馈控制(NLSEF)与输入e连接;扩张状态观测器(ESO)的输出z2先与补偿系数1/b0做积,再和非线性状态误差反馈控制(NLSEF)的输出u0做差,所得信号w为ADRC控制系统的输出信号;同时,输出信号w分别与1/z(z为延时常数)、b0相乘后,作为反馈与扩张状态观测器(ESO)的输入信号u相连;扩张状态观测器(ESO)的输入信号y为被控对象的实际输出反馈信号。

2.2 四色套准自抗扰控制系统设计

根据式(19)四色套准误差数学模型,将图3的控制系统封装成子系统,与自抗扰控制器组合形成自抗扰四色套准控制系统,如图4所示。

每个控制系统包括两个输入v和y,一个输出w,v为微分跟踪器的输入,y为扩张状态观测器的输入,w为扩张状态观测器的输出。三个控制系统与数学模型结合成自抗扰控制器,三个控制系统的输出作为数学模型的输入,分别与数学模型的V2(t)、V3(t)、V4(t)连接;数学模型的套准误差E12(t)、E23(t)、E34(t)分别作为三个控制系统的反馈信号,分别与每个控制系统的输入y相连;每个控制系统的另一个输入v是允许误差参考值输入,理论上讲没有误差时应为零值,故v2、v3和v4应为零值。

图4 自抗扰四色套准系统图Fig.4 Four colors register system structure with active disturbance rejection control

四色套准误差模型有五个输入,分别为机组一至四的输入速度V1(t)～V4(t),以及牵引段的张力输入T0;七个输出分别是一二色的套准偏差E12(t)、二三色的套准偏差E23(t)、三四色的套准偏差E34(t)和牵引段料带张力输出Out_T0、一二色机组间料带张力输出Out_T1、二三色机组间料带张力输出Out_T2以及收卷部分料带的张力输出Out_T3。对四色套准误差模型机组二、机组三和机组四分别加上自抗扰控制器以控制V2(t)、V3(t)和V4(t),机组一做为参考输入无需控制器,速度波动干扰可从V1(t)输入,张力波动干扰从T0输入;输出套准误差分别反馈至对应自抗扰控制器构成闭环系统,控制器通过计算反馈套准误差值大小来实现对机组速度V2(t)、V3(t)、V4(t)的微调,直到套准误差检测器检测到的套准误差数值小于0.1 mm为止,这样反复调整直到套准误差的输出值满足要求。

3 仿真与实验验证

3.1 张力干扰仿真

理论上,印刷过程中料带张力应保持不变,可实际印刷中由于各种不可预测因素的存在,料带张力会发生波动,张力控制系统调节波动的张力,使之短时间内恢复到原来的平衡状态以实现正常印刷。因此,在正常的印刷过程中,料带张力保持一种平衡状态,干扰随机发生且持续时间较短,用脉冲信号作为干扰输入更具有代表性。

仿真模型中E为料带弹性模量,A表示料带横截面积,R为滚筒半径,L为相邻两色机组中心距,参数取值如表1所示。印刷速度取300 m/min,预设张力值100 N,在5 s时刻加载脉冲干扰15 N,持续时间3 s,套准仿真曲线如图5所示。

表1 仿真模型参数表Tab.1 Simulation model parameters

图5 自抗扰控制张力干扰各色套准误差仿真曲线Fig.5 Assorted colors register errors simulation curves with tension interference in active disturbance rejection control

由图5各色仿真曲线可以看出,在自抗扰控制器的作用下,没有张力干扰时各色的套准误差为零,当有张力干扰输入时,瞬时最大套印误差约为0.08 mm左右,随后迅速调整至套印误差为零,满足印刷套准误差不大于0.1 mm的精度要求。

3.2 速度干扰仿真

印刷滚筒加工生产过程中,不可避免会有径跳及质心偏差,在高速印刷时,会导致印版滚筒的线速度不一致,从而导致套印不准问题,故仿真验证速度波动下的套准情况十分必要。

模型参数仍取表1所列参数,仿真设置机组在300 m/min印刷条件下,输入一个x=0.05sin5t的正弦速度干扰函数,仿真套准结果如图6所示。

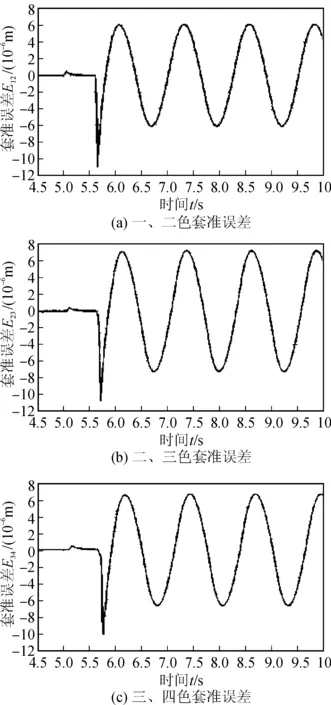
图6 速度干扰套准误差仿真曲线Fig.6 Assorted colors register errors simulation curves with speed interference in active disturbance rejection control

由图6速度仿真曲线可看出,自抗扰控制后各色的套准误差最大值约为0.006 mm左右,远小于印刷套准误差0.1 mm的精度要求。

3.3 实验验证

为进一步验证控制效果,本文设计并购建了凹印机多色套印系统实验平台,主要由机械部分和电气控制两部分构成。机械部分由课题组设计并委托加工组装构成,电气部分采用计算机加运动控制器加私服系统组成,实验系统平台如图7所示。

实验平台选用控制器为ASC Motion Control公司的Pii+NTM-16000004NNNS运动控制器,基于EtherCAT多轴直线运动控制,可同时控制64轴同步运动。

伺服驱动器为UDMba2B04NON1N,伺服电机为意大利PHASE公司的U304.50.2,减速机与光电编码器均为意大利PHASE公司提供,与伺服电机配套使用。机械部分由纠偏装置、放卷装置、印刷装置和收卷装置组成,其中印刷装置四个机组,加上收放卷装置共六个机组配备伺服控制系统。

由于实验平台采用的UDMba2B04NON1N型号伺服驱动器每台驱动器最多可独立控制3台电机,实验设计选取两台伺服器,每台伺服驱动器独立控制3台电机,实验效果以伺服驱动器1所控制的3台伺服电机数据进行验证,伺服驱动器2及其3台伺服电机实验效果不再赘述。

本套准实验通过对不同印刷滚筒表面同一位置的位置差,即同步精度的控制,来模拟验证实际印刷中的套准误差控制。实验平台印刷滚筒直径为60 mm,根据伺服电机编码器反馈信息,每30 000个脉冲滚筒转动一周,则每个脉冲滚筒表面移动0.006 mm,要使滚筒表面位置精度在0.1 mm,须伺服电机位置同步精度控制在17个脉冲内。印刷中,将光电眼反馈套准误差值输入控制器里进行比较,若反馈套准误差值大于0.1 mm,控制器需向伺服电机发送指令以控制其速度,反之,则伺服电机无需调整。